应用MMR的平行度几何评定

2020-03-28鲁周抗黄美发唐哲敏

机械设计与制造 2020年1期

鲁周抗，黄美发，唐哲敏，宋励

（桂林电子科技大学机电工程学院，广西桂林 541004）

1 引言

公差原则是处理尺寸公差与形位公差之间关系的原则，包括独立原则（IP）、包容要求（ER）、最大实体要求（MMR）、最小实体要求（LMR）和可逆要求（RPR）[1]。使用不同的公差原则，可以满足不同的功能需求，例如MMR可在零件有可装配性要求时使用。

国内外学者对零件方位公差应用MMR时合格性的评定进行了大量的研究，并获得了相应的成果。文献[2]建立了零件被测要素应用MMR的二维数学评定模型，并实现对虚拟零件合格性的评定。文献[3]建立了三维孔轴类零件公差的软件量规的数学等效式，此时零件被测要素应用MMR或ER。文献[4]研究了三维零件被测要素有MMR的方位公差合格性的评定模型，可评定虚拟零件的合格性。前述三种模型主要针对零件被测要素应用MMR时零件合格性的评定，且都未考虑零件的形状误差。

当被测要素的方位公差及其基准应用MMR时，可在零件满足其功能要求的情况下，扩大其几何公差值，降低其加工成本、提高其合格率。然而，对于此种情况下零件的方位误差的评定，还未有一个通用和有效的方法。虽然国家标准GB/T16671-2009[5]中给出了此种情况下的物理评定方法，即通过若干个相关联的物理量具来评定零件方位误差的合格性，但这种方法并没有给出具体的数学模型，且此方法存在以下缺陷：对于小批量生产的产品，使用综合量规检测不划算；综合量规的测量柔性小，特定量规对应特定零件。文献[6]建立了被测要素及其基准有MMR时表面光滑的轴对称零件位置误差评定的数学模型。文献[7]用公差映射法确定了零件被测要素方位公差及其基准有MMR时被测要素方位的空间极限变动范围。文献[8]提出了零件孔特征及其基准应用MMR时位置度误差的评定方法。文献[6-8]只能评定简单零件的定位误差，且未考虑实际零件的形状误差。针对以上问题，研究用虚拟量具对被测要素的平行度公差及其基准同时应用MMR（以下简称MM平行度公差）时零件平行度的评定方法。

2 MM平行度的几何约束

2.1 MM平行度的标注内容

在国家标准GB/T16671-2009[5]中，MM平行度公差的标注形，如图1所示。

图1 MM平行度公差标注Fig.1 Marking of Parallel Tolerances

2.2 MM平行度的几何约束

MM平行度公差对被测孔和基准孔有以下5个约束：（1）被测孔和基准孔的局部尺寸应分别处于各自最大实体尺寸和最小实体尺寸之间；（2）被测孔和基准孔不得违反其各自的最大实体实效边界（MMVB）；（3）被测孔MMVB与基准孔MMVB轴线平行；（4）被测孔的最大实体实效尺寸（MMVS）等于其最大实体尺寸减去其平行度公差值；（5）基准孔有形状公差且应用MMR，基准孔最大实体实效尺寸等于其最大实体尺寸减去形状公差值。

2.3 MM平行度的物理检验方法

在满足约束1的情况下，可通过国家标准GB/T 1958-2004[9]给出的物理检验方法对MM平行度进行检测。该方法主要是将零件基准孔套在其相对应量规（位置固定）中，然后调整零件，只要能使塞规通过被测孔，即可判定MM平行度公差合格。此时，基准孔量规的直径等于其最大实体实效尺寸，被测孔塞规的尺寸等于其最大实体实效尺寸，且量规与塞规处于平行位置。

3 MM平行度的数学评定方法

3.1 虚拟量具的数学模型

根据2.3节所述综合量规的几何特性建立相应MM平行度公差的虚拟量具，如图2所示。

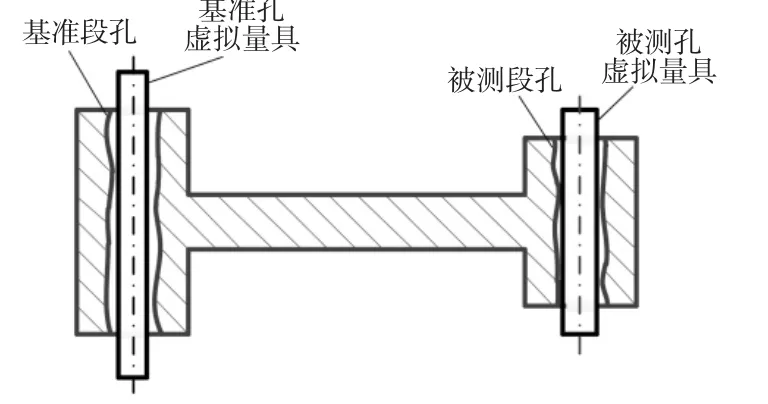
图2 基准孔和被测孔的虚拟量具Fig.2 Virtual Measuring Tool for Datum Hole and Measured Hole

由（4）可得被测孔虚拟量具关键尺寸MMVBB的直径DB为：

式中：DBmax—被测孔的最大实体尺寸；T2—被测孔的平行度公差。

由（5）可得基准孔虚拟量具关键尺寸MMVBA的直径DA为：

式中：DAmax—基准孔的最大实体尺寸；T1—基准孔的形状公差。

3.2 MM平行度合格性评定模型

根据2.3节MM平行度的物理检测方法以及3.1节所建立的虚拟量具模型，可通过以下步骤评定MM平行度公差，如图3所示。

图3 MM平行度公差的评定流程Fig.3 Evaluation Process of M-M Parallel Tolerance

（1）获取被测零件的测点并将其移至局部坐标系中。具体操作，如图4所示。根据式（3）先将实际被测零件几何中心粗略地平移至局部坐标系原点（第一次移动）；

式中：PB，n=（xB，n，yB，n，zB，n）T、PB，n，1=（xB，n，1，yB，n，1，zB，n，1）T—被测孔上序号为n的测点的初始坐标、经第一次移动后测点的坐标；pA，m=（xA，m，yA，m，zA，m）T、pA，m，1=（xA，m，1，yA，m，1，zA，m，1）T—基准孔上序号为m的测点的初始坐标值、经第一次移动后测点的坐标。

然后，再经过调整使第一次移动后实际基准孔的拟合圆柱轴线与局部坐标系z轴重合，如图4.2所示。为了降低编程和评定过程的复杂程度，采用最大内接圆柱法拟合实际基准孔的测点，其数学模型如下：

式中：max dA，m—以局部坐标系原点为圆心的最大内接圆的直径，其值等于实际基准孔的最大内接圆柱的直径；（x1，y1，0）T—实际基准孔的测点沿各坐标轴第二次移动的平移矢量。

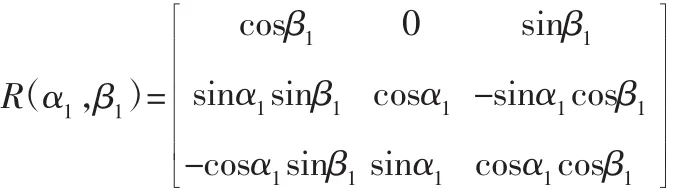
式中：α1、β1—实际基准孔的测点绕x轴、y轴的旋转弧度；目标优化问题的最优解为 xr、yr、αr、βr。

第二次移动后实际被测孔测点坐标PB，n和实际基准孔测点坐标 pA，m可由式（5）求得：

（2）由式（1）、式（2）分别计算基准孔与被测孔虚拟量具的关键尺寸 DA、DB。

图4 基准孔的几何中心及其拟合圆柱轴线移动过程Fig.4 The Movement of the Geometric Center of the Datum Hole and the Fitted Cylindrical Axis

（3）由式（6）检验实际基准孔和实际被测孔是否满足约束1。

式中：DAmin—基准孔的最小实体尺寸；

DBmin—被测孔的最小实体尺寸。

（4）通过计算实际被测孔的极限当量直径来判断被测孔平行度误差是否合格。实际被测孔的极限当量直径：当实际基准孔包容MMVBA时，以平行于MMVBA轴线为轴线、能被实际被测孔包容的最大理想圆柱直径。实际被测孔的极限当量直径可用如下目标优化问题求得：

maxd

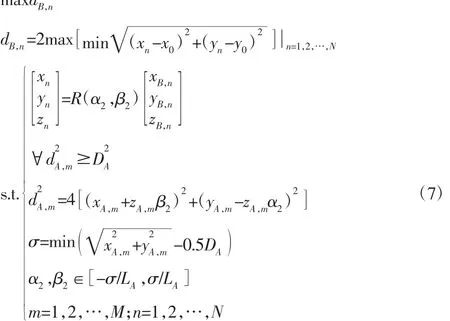
式中：（x0，y0）—零件第三次移动过程中某一位置的实际被测孔投影在局部坐标系xOy平面的最大内接圆的圆心；dB，n—该位置的实际被测孔最大内接圆柱的直径，其轴线与基准孔的虚拟量具的轴线平行；max dB，n—实际被测孔的极限当量直径；dA，m—实际基准孔上序号为m的测点所形成圆的直径。由于α2、β2是实际基准孔第三次移动时分别绕x轴和y轴的微小旋转量，故可作简化处理，即 sinα2≈α2、sinβ2≈β2、cosα2≈1、cosβ2≈1。

若式（8）成立，则可判定被测零件M-M平行度公差合格。

3.3 粒子群算法

针对式（4）和式（7），可用粒子群算法（PSO）来对它们进行求解。粒子群算法计算过程如下：

（1）设粒子群由N1个粒子组成，给定它们的初始位置

（2）跟踪各粒子的局部最优位置Pn1和所有粒子的全局最优位置Pg；

（3）根据式（9）更新各粒子的位置和速度。

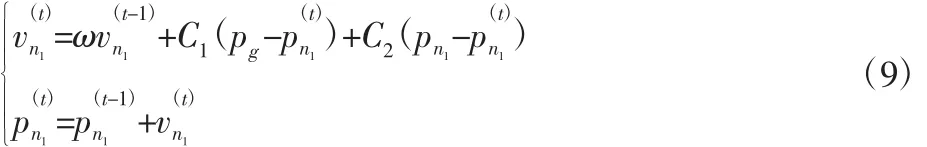
时的位置；t=1，2，…，T；T—最大的迭代次数；ω—惯性权系

数；C1和C2—局部权系数和全局权系数。

（4）粒子的迭代次数若达到给定的最大迭代次数，则结束迭代并输出最终的全局最优函数值，否则进入第（t+1）次迭代。

4 实例分析

某连杆的初步规范，在本节将使用上述所提出的MM平行度公差评定方法对该连杆大小孔中心线的MM平行度进行评定，如图5所示。

评定过程如下：

（1）首先通过三坐标测量机获取被测孔与基准孔的测点数据：分别在基准孔体与被测孔体上测得6层测点，每层包含均匀分布的8个测点，由于篇幅有限，部分测点数据，如表1所示。然后将测点数据代入式（3）将被测零件的测点向局部坐标系原点粗略平移，并将第一次移动后基准孔测点数据 pA，m，1代入式（4），用PSO算法对目标问题进行求解，解得实际基准孔的最大内接圆柱的直径max dA，m=64.010mm，此时最优解（xr，yr，αr，βr）=（-0.6924，0.2776，0.0121，0.0147）。将第一次移动后基准孔和被测孔测点数据，以及（-0.6924，0.2776，0.0121，0.0147）代入式（5），解得第二次移动后基准孔与被测孔测点数据。