基于BP神经网络和证据理论的离心压缩机喘振诊断方法

谢 林，冯 坤，张 明

（北京化工大学机电工程学院，北京 100029）

1 引言

离心压缩机是石油化工生产中的核心动力设备，然而运行过程中易发生喘振故障，喘振发生时，气流周期性振荡作用容易造成转子和密封等部件的碰磨或疲劳损坏[1-3]，进而引发事故。对于离心压缩机喘振故障诊断，传统方法采用时频分析法，通过分析转子不同部位及不同方向的振动信号时域特征、频域特征、以及流量和压力等信号特征[4-6]，进而得出诊断结论，诊断方法过程，如图1所示。如：文献[7]针对茂名石化乙烯全密度装置K-4003循环所压缩机喘振事故，分析机组故障发生时振动变化，从而研究喘振诊断方法；文献[8]通过对两起离心压缩机旋转失速故障实测数据和获取的振动图谱分析，得出离心压缩机喘振故障特征，从而运用喘振的诊断中；文献[9]分析离心压缩机喘振和旋转失速的故障频率和流量特征，由此进行喘振故障诊断。

由于喘振是由旋转分离发展形成的，而机组局部旋转分离时，故障信号特征不明显，故障不易被发现。然而，采用传统方法通常在喘振完全发生后、产生严重的旋转分离，才诊断出来故障[10-11]，这对保护压缩机安全可靠、实现压缩机有效地防喘造成困难。

对此，提出基于BP神经网络和多源信息融合的离心压缩机喘振诊断方法。该方法使用故障数据训练得到BP神经网络，进而对采集的数据初步诊断，再采用证据理论融合初步诊断结论得出诊断结论，从而在喘振完全发生前诊断出喘振故障，为防喘提供相应的决策支持。

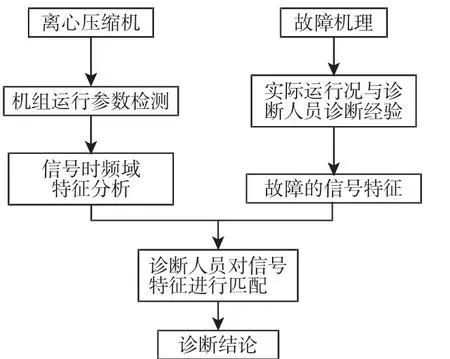
图1 传统故障诊断方法流程Fig.1 Traditional Method of Fault Diagnosis

2 BP神经网络和证据理论

2.1 BP神经网络结构

神经网络是指采用人类大脑神经元结构进行数据处理与分析的模型，BP神经网络是其中重要的模型之一，其结构，如图2所示。

图2 BP神经网络模型Fig.2 BP Neural Network Model

BP神经网络模型包括输入/输出模型、作用函数模型、误差计算模型和自学习模型。

（1）节点输出模型

隐节点输出模型为：

输出节点模型输出模型为：

式中：f—非线性作用函数；q—神经单元阈值。

（2）作用函数模型

作用函数是上下层之间作用强度的关系函数，一般为（0，1）内连续取值Sigmoid函数：

（3）误差计算模型

误差计算模型是反映期望输出与计算输出之间误差大小的函数：

式中：tpi—期望输出值；Opi—计算输出值。

2.2 D-S证据理论

证据理论（Evidence Theory）是一种有效的处理不确定性问题的方法，比传统的概率论方法能更好地把握问题的未知性和不确定性。

证据理论包含以下要点：基本概率赋值函数m、信任函数bel和似真函数pl。设Θ是识别框架，如果集函数m：2Θ→［0，1］满足：

则，m即为识别框架Θ上的基本信任分配函数：∀A⊂Θ，m（A）称为A的mass函数，表示A的信任程度的大小。式中：2Θ为Θ的幂集。

对于∀A⊂Θ，满足式（6）的函数bel定义为幂集2Θ上的信任函数；满足式（6）的函数pl定义为幂集2Θ上的似真函数。

信任函数bel（A）表示证据完全支持A的程度；似真函数pl（A）表示证据不反对A的程度，［bel（A），pl（A）］称为A的信度区间，表示A的不确定程度，如图3所示。

图3 信息的不确定性表示Fig.3 Uncertainty Representation of Information

2.3 D-S证据融合理论

根据D-S证据理论融合理论。设bel1和bel2为同一识别框架Θ上的信任函数，m1和m2分别为对应的基本可信度分配函数，焦元分别为 A1，A2，…，Ak和 B1，B2，…，Bk，则：

3 基于BP神经网络和D-S融合理论离心压缩机喘振诊断方法

3.1 喘振故障传统诊断方法分析

离心压缩机通常具有配套的运行监控系统，传统方法即通过对监控系统采集的信号进行分析诊断，结合喘振发生时故障特征进行诊断，下面以某石化循环氢压缩机组喘振案例对传统进行分析。该机组于2014年5月7日凌晨2点左右发生喘振，防喘阀启动不够及时，导致机组振动过大，进而紧急停机保护机组。

机组概貌，如图4所示。由透平驱动压缩机工作，喘振发生过程中轴振监测，如图5所示。喘振发生过程中流量变化，如图6所示。由上可分析得出，传统诊断方法通过对监控系统采集的信号分析，很大程度上依赖于信号明显的故障特征，如振动大幅上升，或流量大幅下降后，然而此时喘振已经发展到严重阶段，因而此时采取防喘措施已经无法达到防喘的目的。

图4 循环氢压缩机概貌图Fig.4 General Diagram of Recycle Hydrogen Compressor

图5 机组喘振发生过程振动监测Fig.5 Vibration Monitoring of Unit During Surge

图6 机组喘振发生过程流量变化Fig.6 Flow Variation of Unit During Surge

3.1 基于BP神经网络和D-S融合理论的诊断方法

值得注意的是机组运行过程中，喘振初期时振动有轻微的上升，流量也有下降趋势，但由于信号特征不明显，因而很难诊断出喘振故障。若在此时能够诊断出，进而采取相关调控措施，如此即能达到防喘目的。对此，提出基于BP神经网络和多源信息融合的喘振故障诊断方法，该核心是通过BP神经网络的训练，从而在喘振发生初期诊断出故障。方法基本步骤包括：使用喘振故障数据训练得到BP神经网络，进而对采集的数据初步诊断，再采用证据理论融合初步诊断结论得出诊断结论，流程如图7所示。方法详细步骤如下：（1）构建BP神经网络，其输入层节点为in、输出层节点为out、隐含层节点为hidden，设置训练误差e，学习率eta，动量因子mc，使用故障数据训练BP神经网络，得到BP神经网络各层之间连接权值矩阵Wij。（2）确定故障空间，构造识别框架。针对离心压缩机喘振故障，因而故障集：Θ=｛F1，F2｝式中：F1—正常工况；F2—喘振故障。（3）获取离心压缩机轴振动、流量和压力信号，提取所需特征值并构造特征空间的证据体集E=｛E1，E2，…，En｝。（4）将特征空间的证据体集输入到已完成训练的BP神经网络中，得到基本可信度分配函数集 M=｛m1（Fj），m2（Fj），…，mn（Fj）｝，j=1，2。（5）使用 D-S 证据理论融合各步骤（4）所得的基本可信度，得到喘振故障的信任度空间［Bel，Pl］。（6）根据融合诊断决策规则，得出诊断结论。

图7 喘振故障诊断方法流程Fig.7 Surge Fault Diagnosis Method

4 实验验证

本方法使用离心压缩机实验台进行测试，离心压缩机是双支撑的两级压缩机，由变频电机带动齿轮箱驱动，此外实验台还包括：压缩机供油系统、压缩机管网及监测控制系统等，如图8所示。

图8 离心压缩机实验台Fig.8 Centrifugal Compressor Experimental Plant

压缩机轴承箱处分别安装了轴振动传感器，测点号分别1H/1V、2H/2V，H代表水平测点，V代表垂直测点，两者之间夹角90°，置采样频率为5120Hz，采样点数为2048，管道入口处安装流量传感器，进出口处安装压力传感器，压缩机额定运行转速为10000r/min，流量为3000m3/h，吸气压力为0.1MPa，排气压力为0.14MPa，实验测试运行转速7000r/min，通过减小压缩机入口流量模拟喘振故障，采集数据对方法进行测试。

4.1 BP神经网络训练

构建BP神经网，其输入层节点为in=6，输出层节点out=1，隐含层节点为hidden=7，设置训练误差为e=0.001，学习率eta=0.6，动量因子mc=0.8，使用40组喘振故障数据进行训练。经训练得到输入层与隐含层之间的权值（7×7）为的矩阵，如表1所示。隐含层和输入层之间的权值（8×1）为的矩阵，如表2所示。

表1 输入层与隐含层的权值Tab.1 The Weights of Input Layer and Hidden Layer

表2 隐含层与输出层的权值Tab.2 The Weights of Hidden Layer and Output Layer

4.2 BP神经网络计算基本可信度

确定故障空间，构造识别框架。针对离心压缩机喘振故障，因而故障集 Θ=｛F1，F2｝，式中：F1—正常工况；F2—喘振故障。

提取轴振动信号、流量信号以及进出口压力信号特征值，主要分析振动信号均值、方差、有效值、峭度指标和波形指标，对流量、压力信号分析峰值。相同采集周期的特征值构成证据体，5个时间节点分别对应证据体为 E1，E2，E3，E4，E5，由此构成证据体集E=｛E1，E2，E3，E4，E5｝。轴振动特征值，如表 3～表 6 所示。

表3 轴振动1H特征值Tab.3 The Eigenvalue of Shaft Vibration 1H

表4 轴振动1V特征值Tab.4 The Eigenvalue of Shaft Vibration 1V

表5 轴振动2H特征值Tab.5 The Eigenvalue of Shaft Vibration 2H

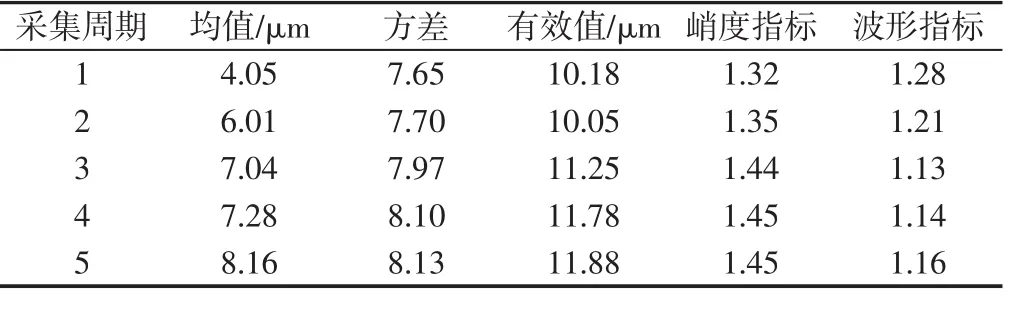
表6 轴振动2V特征值Tab.6 The Eigenvalue of Shaft Vibration 2V

流量、压力特征值，如表 7 所示。将证据体集 E=｛E1，E2，E3，E4，E5｝输入到完成训练的BP神经网络中，其中训练得到表1和表2权值作为BP神经网络的各层之间的连接权值，由此得到基本可信度分配函数集，如表8所示。

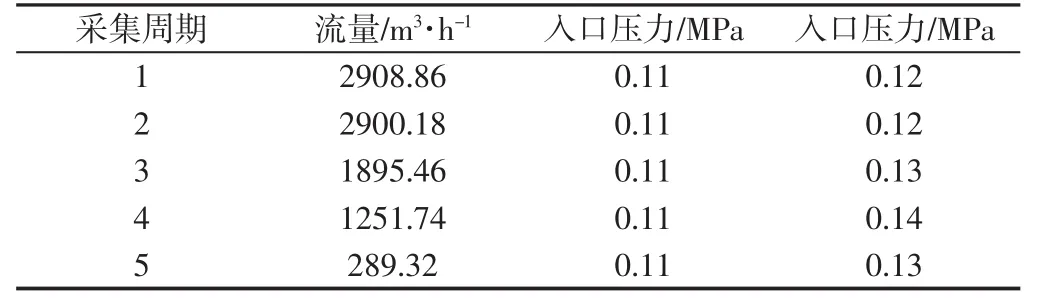
表7 流量、压力特征值Tab.7 The Eigenvalue of Flow and Pressure

表8 基本可信度分配Tab.8 The Basic Probability Assignment

由表8的基本可信度分配可以看出，单一时间节点特征值的证据体对判定是否喘振故障存在较高不确定性，尤其在第三个时间节点，其对应的正常工况的可信度和喘振工况的可信度相当接近，导致无法判定出此时运行工况。将由BP神经网络计算得到的基本可信度分配使用D-S证据理论进行融合，融合结果，如表9所示。从表中可以看出，相比融合前，各时间节点对应的运行工况可信度明显提高，不确定性显著降低。

表9 基本可信度分配融合结果Tab.9 The Fusion Results of Basic Probability Assignment

值得注意的是第三个时间节点喘振可信度明显提升在时间节点上的作用，在第三个时间节点就可以诊断出压缩机发生喘振故障，相对于传统的诊断方法在第五个时间节点发现故障，本方法提早发现了故障。通常在图中第7个时间节点才能诊断出压缩机发生喘振，采用的方法可以在第5个时间节点诊断出，如图9所示。可以从图中发现，压缩机流量逐渐降低正是喘振逐步形成的过程，第5时间节点为喘振发生的初期，而第7时间节点则是已经发生发展到喘振后期。相对喘振后期，喘振初期的危害明显小很多，因而通过这里的方法在喘振初期诊断出故障，进行通过相关控制器进行调控，避免压缩机形成严重喘振，这对于实现离心压缩机防喘、保证压缩机安全运行具有重要意义。

图9 这里方法与传统方法诊断对比Fig.9 Comparison Between Traditional Method and Proposed Method in Diagnosis

为评估基于BP神经网络与证据理论的离心压缩机喘振诊断方法的性能，重复实验取得多组数据，正常工况和喘振工况数据分别取100组数据进行测试结果，如表10所示。从表中可以看出该方法能够准确诊断离心压缩机喘振故障。

表10 多组数据测试诊断结果Tab.10 The Diagnosis Results of Multiple Sets Data

5 结论

（1）针对离心压缩机喘振故障，采用传统时频分析方法诊断，通常在喘振已经发生故障特征明显才诊断出故障，这对压缩机防喘、保护机组安全运行造成困难。对此，提出基于BP神经网络与证据理论的离心压缩机诊断方法。该方法使用故障数据训练得到BP神经网络，进而对采集信号构成的特征集合体初步诊断，得出对应的基本可信度分配，再使用证据理论融合得出诊断决策，从而实现对喘振故障的诊断。（2）使用离心压缩机喘振故障模拟实验数据对提出的方法进行测试，测试结果表明，该方法相比传统方法能提早发现喘振故障，在压缩机喘振初期发现，进而通过调控保护压缩机机组。此外，使用多组数据样本测试该方法，测试表明方法在诊断喘振故障方面具有极高的准确度。