基于公差原则的位置度误差的评定

宋 励，黄美发，唐哲敏，鲁周抗

（桂林电子科技大学机电工程学院，广西 桂林 541004）

1 引言

花键在汽车、机床的变速箱及一般的机械传动装置中应用很广泛，具有很高的位置精度要求[1]。准确的评定其位置度误差，不但可作为零件验收的依据，还可以用来分析误差产生的原因。

确定尺寸公差和形位公差之间关系的原则是公差原则，其中，最大实体要求是体现零件可装配性的一种公差原则，可逆要求应用于最大实体要求的零件[2]，尺寸公差与形位公差相互补偿，改善了被测要素的误差变动范围，能将以前误认为不合格的零件纳入合格品，从而达到降低产品制造成本的目的。

当被测要素的位置度公差应用有最大实体要求、可逆要求时，可以用物理量规来检测产品几何特征的合格性[3]。但是专用综合量规检测不能测出被测要素的实际尺寸和形位误差的大小，并且一个尺寸型号的产品对应一个尺寸型号的综合量规，测量柔性小[4]。文献[5]首先提出了虚拟量具的概念，并建立了被测要素有M的二维数学模型。文献[6]根据产品检测与设计标准的一致原则，提出了满足公差检测一致性要求的软件量规数学表达式。文献[7]通过模拟量规与产品的虚拟测量过程来分析产品基准参考框架的建立问题。

上述模型都是以实际基准特征要素来建立基准的，而较少涉及有公差原则的参考基准。当被测要素的基准遵循公差原则时，基准要素在遵循的边界范围内浮动[3]。国家标准GB/T16671-2009[2]和美国机械工程师协会标准ASME Y14.5-2009[8]规定了被测要素有尺寸公差、方向公差或位置公差和M，并且其基准有M的情况。该情况可以通过相关联的若干个量规对其合格性进行检验，但是此方法主要用于大批量生产或位置度要求不高的零件。

为了提高检测方法对花键零件结构和尺寸的适应性，同时解决基准应用有公差原则的位置度误差评定问题，将建立相应的虚拟量具的数学模型并提出位置度误差合格性评定的数学方法。

2 花键轴M-MR位置度的几何约束

M-MR位置度公差的标注，如图1所示。

图1 花键位置度公差标注Fig.1 The Position Tolerance Annotation of the Spline

花键轴M-MR位置度公差对被测要素和基准要素有，如下5个要求[2]：（1）花键的提取要素不得违反其最大实体实效状态MMVC，其宽度为最大实体实效尺寸MMVS。（2）花键的提取要素各处的局部尺寸应大于最小实体尺寸LMS，可逆要求RPR允许其局部尺寸从MMS增大至MMVS。（3）各个花键的最大实体实效边界MMVB的中心平面通过基准的最大实体实效边界MMVB2的中心轴线，且各个键的理想中心平面分别位于等分位置上。（4）基准要素的提取要素不得违反其最大实体实效状态MMVC，由于基准要素的导出要素没有标注几何公差要求，其最大实体实效尺寸MMVS为最大实体尺寸MMS。（5）基准要素的提取要素各处的局部直径大于最小实体尺寸LMS。

3 M-MR位置度的数学评定方法

为了与GB/T1958-2004[9]给出的综合量规的理想几何特性保持一致，M-MR位置度公差的虚拟量具由被测花键键宽的最大实体实效边界MMVBn和基准小径的最大实体实效边界MMVBd构成。

3.1 虚拟量具的数学模型

该花键检测量规模型由被测要素和基准要素的最大实体实效边界构成，各个花键的最大实体实效边界MMVB的中心平面通过基准的最大实体实效边界MMVBd的中心轴线，且各个键的理想中心平面分别位于等分位置上，同时构建局部坐标系，将MMVBd的轴线置于局部坐标系Z轴，轴上任取一点置于局部坐标系原点，确定虚拟量具的方位[10]。

3.2 花键的合格性评定

基于3.1节所述的虚拟量具，按以下步骤对花键的M-MR位置度误差进行评定。

3.2.1 将实际被测花键的测量坐标置于局部坐标系中

首先将花键的三坐标测量数据进行粗略平移，如式（1）所示：

式中：Pd，m=（xd，m，yd，m，zd，m）T—实际基准小径键槽面上的测点数据；m—测点序数；Fi=（xi，yi，zi）T、Bi=（xi，yi，zi）T—实际基准小径圆柱体的前端面和后端面上的测点数据；i—测点序数；PBn，L，a=（xBn，L，a，yBn，L，a，zBn，L，a）T、PBn，R，a=（xBn，R，a，yBn，R，a，zBn，R，a）T—实际被测花键n左侧面和右侧面上的测点数据；a—测点序数；n—键序数；Fn，a=（xn，a，yn，a，zn，a）T、Bn，a=（xn，a，yn，a，zn，a）T—实际被测花键n前端面和后端面上的测点数据；a—测点序数；n—键序数—粗略平移后的坐标数值；Pd，1/2—Fi、Bi连线的中点，在实际基准小径圆柱体两个端面的对称平面上。

通过上述的粗略平移之后，再进行旋转平移，采用最小外接圆柱来拟合实际基准小径，具体的拟合目标函数，如图2所示。

图2 实际基准小径的拟合Fig.2 The Actual Datum for Fitting

图中：dm—最小外接圆直径；L—花键的名义长度。目标优化：

式中：（x0，y0，0）—实际基准圆柱移动时的平移向量；α0、β0、δ0—实际基准圆柱时绕局部坐标系x轴、y轴和z轴的旋转弧度。

为旋转矩阵，体现每个测点绕局部坐标系x、y、z轴依次旋转α0、β0、δ0弧度而引起的坐标变动。

采用粒子群算法进行求解，解得最优解（x0，min，y0，min，z0，min，α0，min，β0，min，δ0，min），即实际基准小径 d2的拟合圆柱体 M2对应的（x0，y0，z0，α0，β0，δ）0的值，目标优化问题的最优值 mindm是实际基准小径圆柱的最小外接圆柱的直径。

通过式（2）的坐标转换可分别得到实际被测花键n左侧面和右侧面相对于拟合基准圆柱体M2的坐标集

3.2.2 计算虚拟量具的关键尺寸

被测花键的最大实体实效边界MMVBn的键宽BVn和基准小径的最大实体实效边界MMVBd圆柱体MV2的直径Dv2。

键宽 BVn=Bn+esn+T，直径 Dv2=d2+es2。

3.2.3 计算实际被测花键的极限当量键宽 Bn，2M，coa，mM

图3 被测花键的极限当量键宽Fig.3 The Limitation Equivalent Spline Width of the Measured Spline

图4 被测花键的等分位置Fig.4 The Equal Distribution of the Measured Spline

实际被测花键的极限当量键宽是指：当基准小径的最大实体实效边界MMVBd包容实际基准小径d2圆柱体时，以MMVBd的轴线为花键的基准轴线，能包容实际被测花键的理想花键的最小键宽，理想花键的中心平面通过MMVBd的轴线，且各个键的理想中心平面分别位于等分位置上。

以实际基准小径d2相对于圆柱体MV2的三维空间姿态v2为变量，以实际被测花键键宽Bn相对于圆柱体MV2的当量键宽Bn，2M，coa=f（v2）为目标函数进行目标优化，得到实际被测花键Bn相对于圆柱体 MV2的极限当量键宽 Bn，2M，coa，mM。

该过程可以用目标优化问题（3）表述如下：

式中：（dx，dy，0）—实际基准圆柱移动时的微小平移向量；dα、dβ、dδ—实际基准圆柱移动时绕局部坐标系x轴、y轴和z轴的旋转弧度；R（dα，dβ，dδ）=旋转矩阵；dv2，m—实际基准圆柱体上的第m个测点到局部坐标系z轴的距离的二倍，该值不能大于基准小径最大实体实效边界MMVBd的直径 Dv2；

目标优化问题的最优值 Bn，2M，coa，mM=minBn，2M，coa是实际被测花键的极限当量键宽。

3.2.4 判断被测花键的位置度是否合格

当实际被测花键的极限位置处的当量键宽 Bn，2M，coa，mM均不大于花键的MMVBn的宽度Bvn，意味着实际零件能通过虚拟量具。

4 实例验证

某型号花键轴零件的尺寸与几何公差的初步规范，如图5所示。实际零件在三坐标测量机上的测量数据，如表1、表2所示。

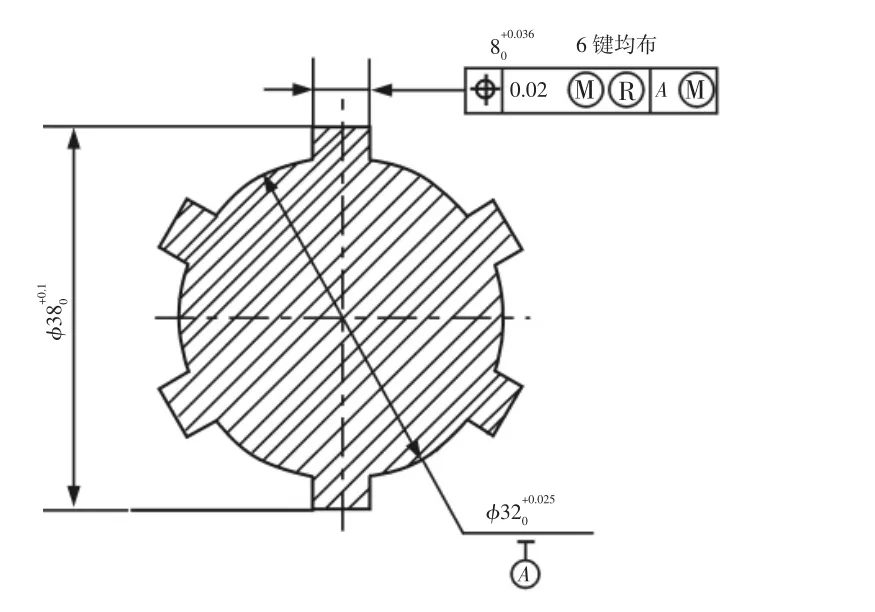
图5 某花键轴的尺寸与几何公差的初步规范Fig.5 The Tolerance Annotation of the Measured Spline Shaft

表1 花键轴的端面测量数据Tab.1 The Measurement Data of the End Surface of the Spline

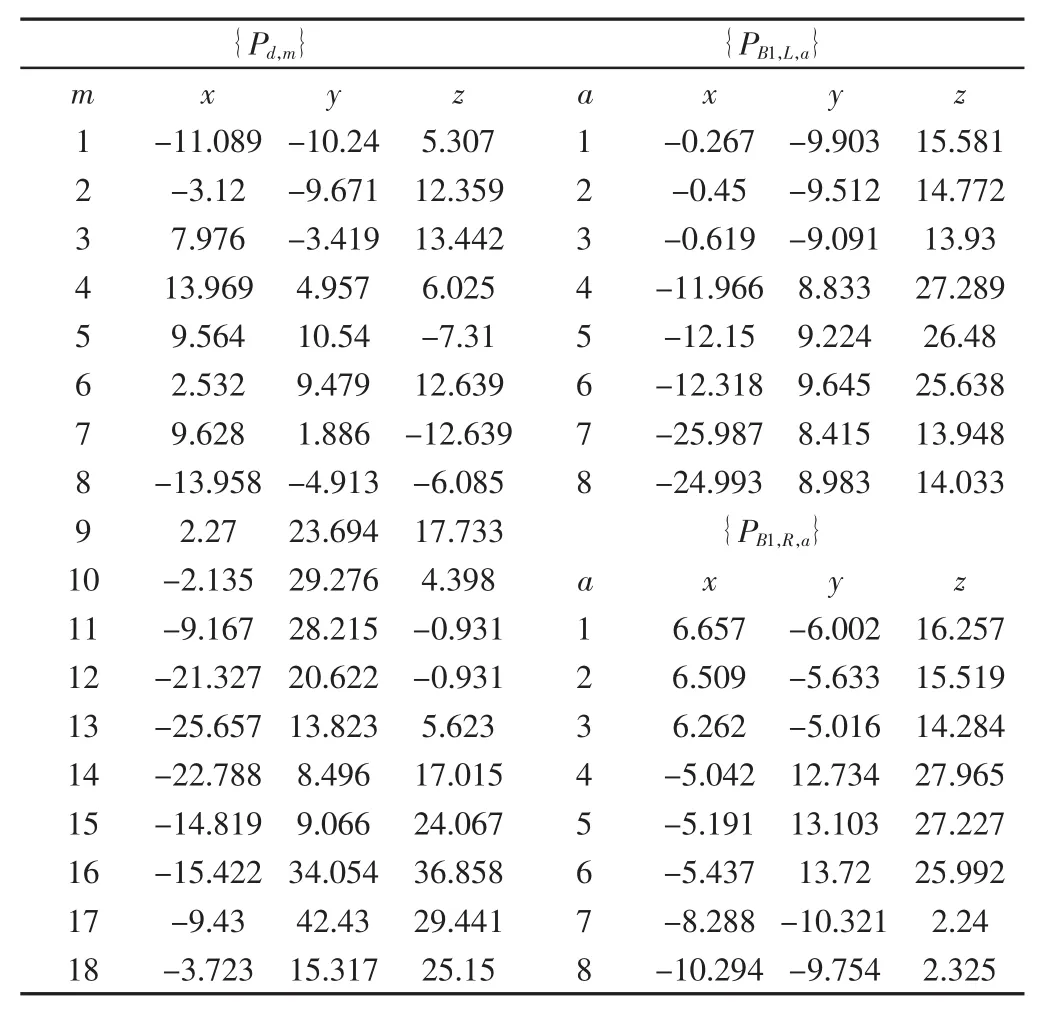
表2 键槽面和花键侧面的测量数据Tab.2 The Measurement Data of the Keyway Surface of the Spline and the Side Surface of the Spline

4.1 步骤1将实际被测花键的测量坐标置于局部坐标系中

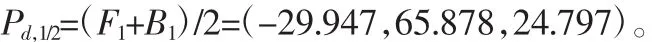
将实际基准小径上获得的测点数据集拟合成小径圆柱体M2，求得实际基准小径圆柱的最小外接圆柱的直径：mindm=32.0628mm，最优解：（xo，min，y0，min，α0，min，β0，min，δ0，min）=（14.2538，15.6679，0.0263，0.0131，0.0273）。

4.2 步骤2计算虚拟量具的关键尺寸

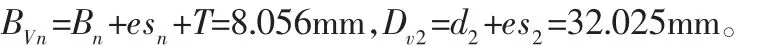
4.3 步骤3计算实际被测花键的极限当量键宽Bn，2M，coa，mM

解得实际被测花键的极限当量键宽 Bn，2M，coa，mM=minB1，2M，coa=8.0152mm，以及相应的最优解（dx，dy，dα，dβ，dδ）=（0.0346，0.0346，0.00231，0.00231，0.00231）。

4.4 步骤4判断被测花键的位置度是否合格

当实际被测花键的极限位置处的当量键宽 Bn，2M，coa，mM均不大于花键的MMVBn的宽度Bvn，意味着实际零件能通过虚拟量具。

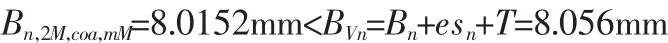
5 结语

根据被测花键轴的基准有最大实体要求，被测要素有最大实体要求、可逆要求的位置度公差的工程语义，分析实际量具的几何特性及其在合格性评定中的使用过程，建立相应的虚拟量具的数学模型并提出合格性评定的数学方法。该方法有效地解决了基准要素上应用公差原则的位置度误差的评定问题，同时为确定花键的位置精度提供了必要的理论依据。