三指灵巧手结构设计及接触力规划

蔡 博，高宏力，宋兴国，王奉晨

（西南交通大学机械工程学院，四川 成都 610031）

1 引言

随着机器人领域的不断扩大与智能制造的快速发展，机械手作为机器人的末端执行器同时也是和环境直接接触的唯一对象，它的发展也从早期的夹持器逐渐向着多手指、多关节、具有一定感知功能的现代意义仿人灵巧手的方向转变，尤其是手指的灵巧性设计方面，如手指结合尺寸、关节数目、驱动、传动方式的选择和传感器系统设计等[1-3]。显然，多指灵巧手以其多自由度、多手指及具有感知功能的特点是可以满足机械手发展要求的。机械手最为显著的功能显然是具有人手一样的抓取，对机械多指手的抓取力规划研究成为了在多指手抓握与协调控制上的关键。

针对一般灵巧手由于追求灵巧性与外形尺寸过大、结构过于复杂之间的矛盾，在分析其驱动结构、传动结构及相关装配的基础上，设计了一种灵活性高尺寸小的全驱动三指灵巧手，包括对关节电机的选型，建立动力学、静力学方程，对其进行三维建模，运动ADAMS对其进行动力学仿真以验证灵巧手结构设计及电机选型的合理性；在设计灵巧手的结构基础上，运用一种简单有效的接触力求解方法对其进行接触力规划求解，验证得到的接触力在关节力矩驱动下的合理性。

2 三指灵巧手总体结构设计

2.1 总体方案设计

根据常见的机械手抓取姿势，设计了一种体积小、灵活性高的三指全驱动机械灵巧手。灵巧手的所有关节均为转动关节，选用的驱动为小巧而强劲的Maxon直流伺服电机以及配套的减速器。整个机械灵巧手的结构特点如下：

（1）整个机构简单、结构紧凑及轻巧，手指主要由关节外壳、电机、减速器及电机座组成，只预留4mm的空间，使关节结构紧凑轻巧；（2）灵巧手共有八个自由度，具有高度的灵活性，通过三个手指的配合，可以实现日常大多数的抓取功能，包括抓、握、捏、夹、包络等；（3）采用直流伺服电机驱动与锥齿轮传动，传动可靠，控制精度高，尺寸小，集成度高。

2.2 三指灵巧手结构设计

根据总体设计方案，对灵巧手的结构进行了设计，灵巧手由三个手指、手掌和底座等组成，其中外围两个手指通过底座上的直流伺服电机驱动进行侧摆运动，手指的弯曲则通过关节的内置驱动电机完成，中指关节长度为55mm，远指关节长度为35mm，整个灵巧手机构三维模型，如图1所示。

灵巧手通过基座电机控制外围两手指的旋转侧摆动作，侧摆转过合适的角度与中间手指配合完成常见的抓、握、捏、夹、包络等动作，使得灵巧手对不同形状的物体有着较好的适应性；基关节中蜗轮蜗杆的使用不仅实现基关节运动的换向，同时也起着驱动电机的减速效果；远指关节的弯曲则由内置于中指关节的电机配合锥齿轮驱动完成，电机减速器由电机座固定于关节内部，其输出轴端则由轴套配合顶丝对其进行轴向固定；和中指基座固定连接的手掌一方面可以配合手指对物体进行包络动作，起着限位的作用；另一方面则起着保持另外两个手指基座的平衡与稳定。整个机构结构紧凑，尺寸小巧，灵活性高。

在三指手的结构功能上，它可以完成大多数常见的抓取动作，各手指均采用小巧而强劲的Maxon电机驱动，通过减速箱、蜗轮蜗杆、锥齿轮和连杆将运动和力传递到每个指节，实现三指手的关节运动和物体抓取。

图1 灵巧手三维模型Fig.1 Three-Dimensional Model of Dexterous Hand

图2 中指关节结构Fig.2 The Structure of Middle Finger Joint

3 动力学建模及仿真

3.1 动力学方程的建立

进行动力学分析的方法很多，包括拉格朗日法、牛顿-欧拉法、高斯原理法等，拉格朗日方法不需要关注各部分间的内力，具有显示结构，物理意义明确，因此采用拉格朗日法进行动力学分析。

拉格朗日动力学方程模型：

式中：拉格朗日函数L=K-P，K—手指的动能；

P—手指的势能；

qi—关节变量；

Fi—关节的驱动力矩。

根据三指手的结构特点，将单手指结构简化等效为平面二连杆机构，其结构，如图3所示。

图3 灵巧手部分简易模型Fig.3 Simplified Model of Dexterous Hand Part

由拉格朗日方程分析很容易知道系统的总动能和总势能分别为：

以上得到的动力学方程做了一些简化，三指灵巧手中的中指关节与远指关节两个关节简化为质量均匀分布的连杆；忽略了关节之间的摩擦以及将其视为刚体。因此，关节驱动力矩只与关节转角有关，通过关节的运动规律得到关节驱动力矩的大小。

3.2 基于ADAMS的动力学仿真及验证

为避免导入到ADAMS中的机械手由于有较多的零部件及相互配合关系使得在ADAMS中对机械手的分析复杂化，对三维模型进行必要的简化[4]，如图1所示。

图4 灵巧手虚拟样机Fig.4 Virtual Prototype of Dexterous Hand

对导入到ADAMS中的灵巧手模型定义各部分材料属性，在各个转动关节处添加转动副（Joint），在需要固定的位置添加固定副；利用ADAMS提供的step函数对转动副设置驱动（Motion），即为关节转动的运动规律，在每个关节中心处添加Marker点，进行仿真，得到的关节点的速度曲线、关节力矩曲线、关节点位移曲线；由于三个手指在弯曲转动关节是一样的，故添加的驱动函数相同，各关节速度曲线、位移、角加速度等均是一样的[5]。

在3s的时间内，手指关节速度、位移曲线光滑变化平稳，无剧烈振动及突变现象，说明了设计的合理性。

图5 关节速度曲线Fig.5 Joint Velocity Curve

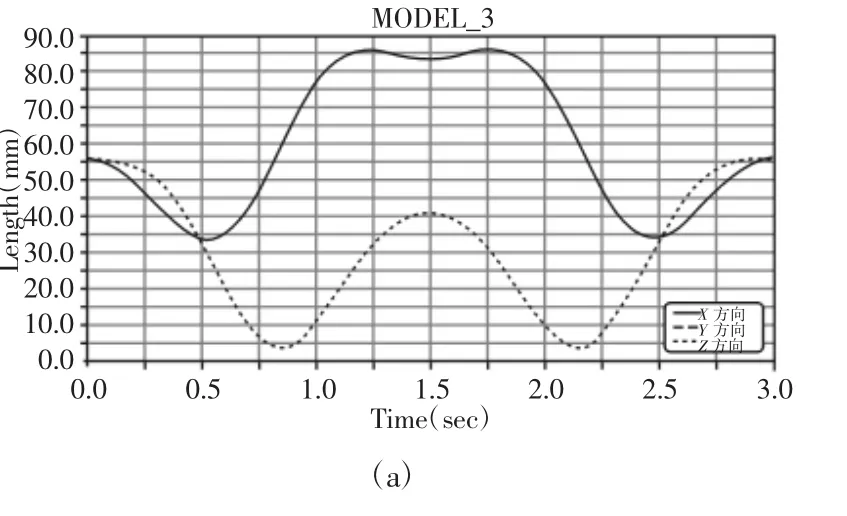
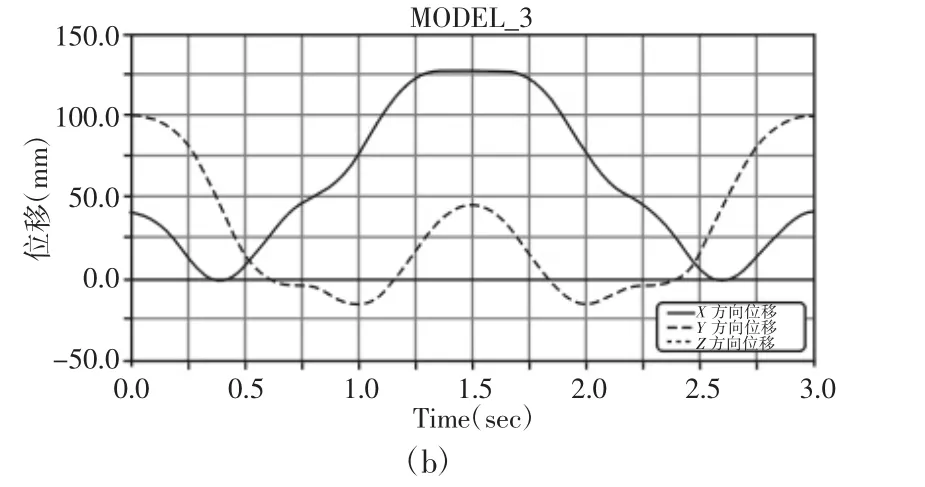
图6 关节位移曲线Fig.6 Joint Displacement Curve

图7 关节力矩曲线Fig.7 Joint Torque Curve

在MATLAB中选取一组离散的时间点，得到对应的力矩值，与导入到MATLAB中的ADAMS仿真力矩曲线进行对比，如图8所示。其理论分析数据和仿真数据的偏差很小，在合理范围内，证明了理论计算和仿真分析的合理性，同时为其电机选型及控制系统设计提供参考。

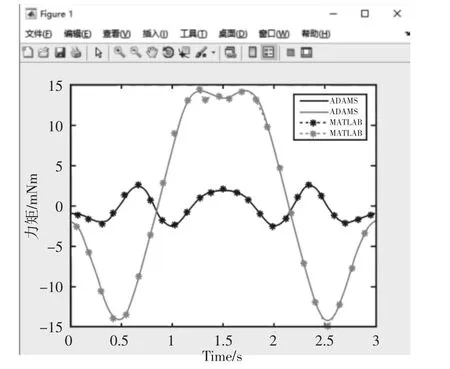
图8 关节X方向力矩理论曲线和仿真曲线的对比Fig.8 Comparison of Moment Theory Curve and Simulation Curve of Joint X Direction Torque

3.3 三指灵巧手静力学分析

灵巧手与外界物体接触时，为确定手指抓取力与关节驱动力矩之间的关系以方便可靠地抓取物体，需要对灵巧手进行静力学分析。在静态条件下，由虚功原理可以知道，关节驱动力矩子和指尖与物体的接触力FP之间的关系为：子＝JTFP，在避免出现奇异状态的条件下，计算灵巧手与外部环境的接触力的关系式为：

从式（5）中可以看出手指接触力与关节驱动力矩以及关节转角之间的关系。考虑到设计的灵巧手结构与抓取性能，其关节转角分为 A∈［-30°，0］，B∈［30°，60°］。在关节驱动力矩即电机力矩选定的条件下，手指接触力FP取决于关节转角，其随关节转角的变化分布，如图9所示。给定了电机驱动力矩，接触力的大小范围随之确定；反之也一样，并且由此可以为电机选型提供参考。

图9 接触力随关节角度的分布图Fig.9 The Distributed Chart of Contact Force with Joint Angle

4 多指手接触力规划与计算

多指手抓取或操作物体时，各手指对物体需要施加一定大小的力以避免抓取力过大对物体造成变形与损伤。文献[6]提出了一种基于抓取力矢量的线性约束梯度流力优化方法，该算法不需要线性化摩擦锥，但需要在迭代前给出满足非线性摩擦锥约束的初始抓取力才能求取最优抓取力。文献[7]提出一种以序列二次规划算法为核心的fmincon函数对非线性规划问题求解，简化了求解过程，但也需要求解对fmincon函数影响很大的接触力初始值。文献[7]提出通过调节手指法向接触力的权值系数来获得满足非线性摩擦锥约束的初始抓取力的方法，该方法简单通用，不过求得初始力后需要结合梯度流算法进行优化，这样就显得比较繁琐。此外，这些算法均没有考虑关节驱动力矩对手指接触力的约束，无法确保优化计算得到的接触力可以由关节力矩提供。

借鉴文献[8]利用格朗日乘子法即通过迭代不断调整其系数来获得满足非线性摩擦锥约束的初始抓取力，然后引入一个稳定对其优化得到多指手抓取力。通过对仿真对比，验证了该方法的有效性。

这里以抓取球体为例，如图10所示。将手指与物体之间的接触视为一般情况下的有摩擦接触，第i个手指与物体之间的接触力可以表示为：FPi=（FPix，FPiy，FPiz）T，FPix、FPiy、FPiz分别为FPi在手指笛卡尔坐标系三个方向的分力。手指接触力FPi与物体受到的合力F0之间为线性映射关系，即为抓取矩阵G∈R6×3m，则有如下静力平衡方程成立：

为实现抓取的稳定性，满足手指抓取的力封闭性，物体需要满足静力平衡条件、满足摩擦锥约束及单项力约束，式（6）给出了抓取的静力平衡方程，摩擦锥约束与单项力约束表示如下：

对于相容性方程（5）而言，其一般解为：

式中：FM—平衡物体受到的外力，即操作力；FN—抓取内力，对手指的抓取稳定性及手指物体之间的接触稳定性起决定性作用；V—任意n维矢量；I—9×9的单位矩阵。

通过式（8），可以推导出，调节内力的大小可以获得满足要求的接触力与较优性能的内力，使得抓取内力不会过大引起物体的虚位移变形，也不会过小导致抓取的不稳定。基于此，构造如下目标函数：

目标函数中的α是调节各手指抓取内力的系数向量，通过动态调节α的大小，可以获得满足摩擦锥约束的初始抓取力。对任意给定的初始 α，以 β（β>1）对其进行线性变换，通过 αk+1＝βαk调整系数向量α的大小，从而得到合适的初始抓取力。由文献[8]可以知道，α即为手指接触力中法向力权值系数。

图10 抓取球体示意图Fig.10 Diagram of Grasping Sphere

根据前面设计的三指灵巧手，选取球的直径为60mm，考虑抓取的稳定性，三指指尖与球体的接触点A、B、C在圆球大圆上均匀分布，手指与球体的摩擦系数为0.3，求出抓取矩阵G为：

抓取矩阵G是行满秩矩阵，从而G+=GT（GGT）-1。设定各接触力的法向力权值系数初值α=0.3，线性变换因子β=1.2，纯外力螺旋F0=［0.15 0.173 0.3 0 0 0］T，则得到满足摩擦锥约束及单项力约束的初始抓取力：

在Matlab中进行验算得：

计算得到的结果均位于手指接触的摩擦锥内，但很明显，接触力与摩擦锥边界很接近，因而并不具备较强的抗干扰能力。定义一个摩擦锥的稳定接触系数λ（λ>1），用于手指抓取的稳定性程度。从而对摩擦锥约束进行修正，这里取λ＝1.2，约束λ，重新计算可以得到各手指接触力：

与优化前的抓取力相比较，引入稳定接触系数λ后，各手指的法向接触力变大，这样使得抓取时可以避免因抓取的细微扰动造成抓取的不稳定，有利于灵巧手的稳定抓取。由前面得到的接触力曲线可以知道，关节驱动力矩是可以满足优化后的接触力的，灵巧手抓取示意图，如图11所示。

图11 灵巧手抓取仿真示意图Fig.11 Grasping Simulation Diagram of Dexterous Hand

5 结论

首先对三指灵巧手进行结构设计，包括对其进行构型、零部件的布置及相关部件的选型，建立其三维模型。然后建立灵巧手单手指动力学数学模型，运用MATLAB对动力学方程进行数值分析并绘制力矩曲线；将模型导入到ADAMS中建立虚拟样机，进行仿真分析，获得其关节力矩曲线、关节点与末端点的速度与位移曲线，分析了灵巧手指的运动状态特性，说明了灵巧手结构设计的合理性；并且将仿真力矩曲线与理论力矩曲线进行对比，偏差较小，验证了动力学理论分析的正确性。利用拉格朗日乘子法求取抓取力初值，对其优化得到了手指抓取力，验证了其在关节力矩约束下的合理性，简化了多指手抓取力的计算。