全陶瓷球轴承内外圈沟曲率系数的优化设计

周井玲，张巍文，顾乐乐

（南通大学机械工程学院，江苏 南通 226019）

1 引言

陶瓷轴承是为解决传统轴承在超高速、耐腐蚀、耐高温及其他恶劣工况下难以胜任的问题而研制的一种新型轴承，在航天、军工和机械加工等领域有着极其广阔的应用前景[1-2]。

陶瓷轴承的设计可以借鉴金属轴承的设计理论。但是，由于陶瓷本身与金属材料属性的不同，设计时决不可以用钢轴承的设计参数生搬硬套。由于陶瓷材料本身对应力较为敏感，在设计轴承的内外圈沟曲率半径系数时，若直接沿用钢轴承的设计参数，则会使球与内外圈的接触应力偏大，降低轴承的疲劳寿命[3-5]。这里就型号为6004的氮化硅全陶瓷深沟球轴承的内、外圈滚道沟曲率系数fi、fe进行优化设计来提高轴承的疲劳寿命。

2 当前设计试样轴承疲劳寿命试验

2.1 试验对象

型号为6004的当前设计试样陶瓷球轴承。

2.2 试验方法

取20个当前设计的试样轴承进行载荷为500N下的疲劳试验，记录试验数据，轴承疲劳寿命试验机具有振动、温度、转速、疲劳寿命监测功能。可设定振动阈值，当振动值大于设定阈值时，认定轴承疲劳失效，试验机自动停止运行。

2.3 试验设备

轴承疲劳寿命试验机，轴承装配方式，如图1所示。

图1 试验设备Fig.1 Test Equipment

2.4 试验条件

轴承润滑方式：无润滑。

径向载荷：500N。

轴承转速：1000r/min。

振动阈值：0.03m/s2。

2.5 试验统计结果

试验结果，如表1所示。

表1 当前设计试样轴承试验统计结果Tab.1 Result of Current Design Bearing Test

3 优化设计方案

通过表1可以看出当前设计轴承的失效方式以内外圈的疲劳剥落为主，在降低内外圈与滚动体接触应力的同时必定会加大内外圈与滚动体之间的摩擦力矩，故对内外圈接触应力以及摩擦力矩进行优化平衡，使轴承寿命有所提升。

目标函数为赫兹接触应力以及旋转摩擦力矩，根据文献[6]采用下列表达式。

由赫兹接触理论有：

式中：P—最大接触应力；

R—综合曲率半径；

Q—接触载荷；

a—接触椭圆的长半轴；

b—接触椭圆的短半轴。

滚动轴承的摩擦来自滚动体与滚道之间的滚动摩擦和滑动摩擦，滚动体、保持架等滑动接触部位的滑动摩擦。在球轴承中，球在套圈上的自旋摩擦占总摩擦的大部分，且远大于其他类型的摩擦[7]。因此，讨论球与内外圈的自旋摩擦力矩：

式中：μ—摩擦系数；

Q—接触载荷；

a—接触椭圆的长半轴；

L（k）—第二类椭圆积分。

设目标函数接触应力以及摩擦力矩的值越小，则轴承寿命越长。令f（x）要求越小越好。用d表示目标函数值对应的功效系数[8-10]。即：

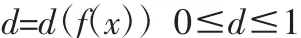
式中：d（f（x））—某项目标函数的功效系数。

且当f（x）达到最优值时d=1，反之d=0。功效系数为：

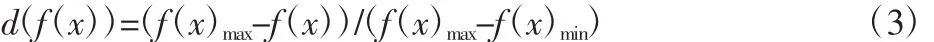
式中：f（x）max，f（x）min—目标函数值的最大值；

x—内外圈沟曲率系数。

各目标函数的功效系数分别为：

式中：Pimin、Pimax、Pemin、Pemax、Mimin、Mimax、Memin、Memax—内圈接触应力、外圈

接触应力、内圈摩擦力矩、外圈摩擦力矩的最小值和最大值。

从表1的统计结果中可以看出磨损失效类型的总数仅为疲劳剥落的1/2，内外圈疲劳剥落失效以及摩擦磨损失效数量之比为4：2：2：1，故确定内圈接触应力、外圈接触应力和内圈摩擦力矩的权重因子比值为4：2：2：1，则可建立如下优化评价系数D：

式中：d1、d2、d3、d4—内圈接触应力、外圈接触应力、内圈摩擦力矩、

外圈摩擦力矩的功效系数。

4 有限元分析结果

以型号为6004的全陶瓷深沟球轴承为算例，原内、外圈滚道沟曲率系数分别为为0.525、0.527。利用MATLAB对D值进行寻优，优化后的内、外滚道沟曲率系数分别为0.518、0.523。使用ANSYS Workbench软件进行分析。

建立有限元实体模型，如图2所示。进行应力分析以及温度分析，所以对优化前后不同径向载荷、不同转速下的有限元分析结果进行对比分析。

图2 有限元实体模型Fig.2 Finite Element Model

不同载荷下内外圈最大拉应力的有限元对比分析，如图3所示。从图中可以看出优化前后内圈所受到的最大接触应力的差值随着径向载荷的增大也越来越大，当径向载荷为600N时，优化后内圈所受的最大接触应力减小了8.7%，约0.47MPa。优化前后的外圈最大接触应力减小了4.4%，约0.12MPa。不同载荷下内外圈摩擦力矩的有限元对比分析，如图4所示。图4中看出优化前后内外圈摩擦力矩的差值均随着载荷的增大而变大，当载荷为1kN时，内外圈摩擦力矩分别升高了21%和19.5%。

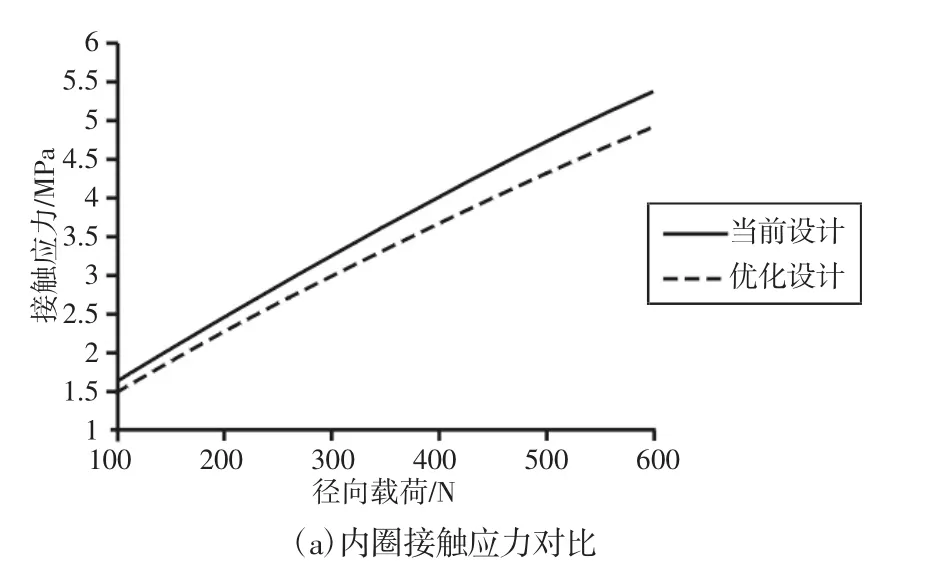
图3 内外圈最大接触应力有限元分析结果对比Fig.3 Comparison of Contact Stress Under Finite Element Analysis

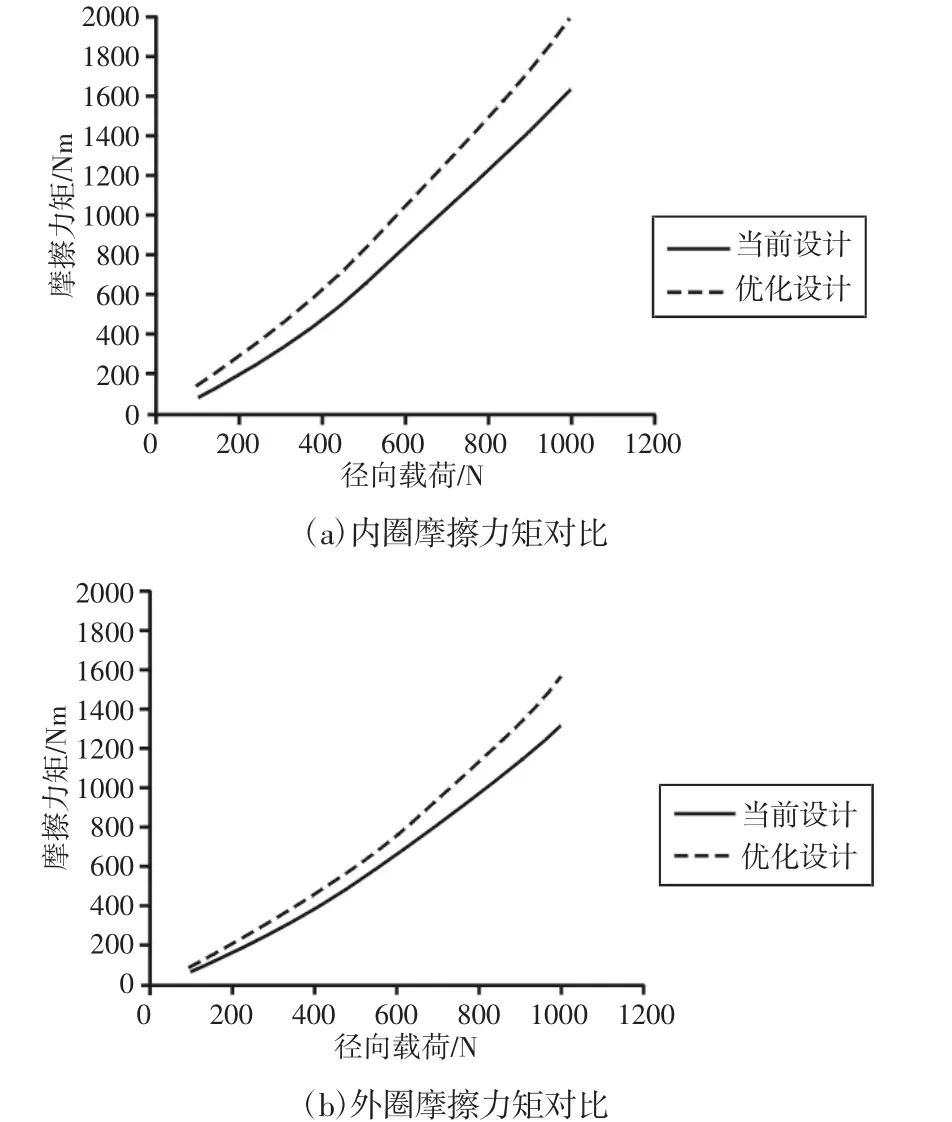
图4 内外圈摩擦力矩有限元分析结果对比Fig.4 Comparison of Friction Moment Under Finite Element Analysis

5 优化前后疲劳寿命试验对比

图5 优化前后疲劳寿命对比Fig.5 Comparison of Fatigue Life Between Current Design and Optimal Design

对优化前后的陶瓷球轴承进行疲劳寿命试验对比。在载荷分别为100N、200N、300N…1000N下进行3次疲劳寿命，总计30次疲劳寿命，记录试验数据。试验条件如下所示，轴承润滑方式：无润滑，轴承转速：1000r/min，振动阈值：0.03m/s2。根据试验数据绘制的曲线，如图5所示。当载荷在（400～700）N之间时，优化设计的轴承寿命提升了17%左右，当载荷<300N或>900N时寿命差值为9%左右。

6 结论

以型号为6004的全陶瓷深沟球轴承为算例进行优化设计。运用轴承疲劳寿命试验机，完成了一组当前设计试样轴承的寿命测试。并对测试结果分析，以球与内外圈的接触应力和摩擦力矩为目标函数，进行优化设计。优化设计前后球与内外圈接触应力和摩擦力矩的有限元分析结果符合预期假设。最后通过试验验证了优化后轴承的疲劳性能有所提升，完成了全陶瓷深沟球轴承内外圈滚道沟曲率系数的优化设计。