一种机械臂分段插值轨迹规划方法

郑 涛 ，刘满禄 ，2

（1.西南科技大学特殊环境机器人技术四川省重点实验室，四川 绵阳 621010；2.中国科学技术大学信息科学技术学院，安徽 合肥 230026）

1 引言

轨迹规划是工业机械臂运动控制系统的重要组成部分，其平滑性直接关系到机械臂末端位姿的精确性。轨迹规划算法的研究是提高工业机械臂末端的精准性和柔顺性的前提，文献[1]中提出的三次样条插值改进算法解决了传统三次样条插值在起始点和终点的加速度突变的情况，文献[2]中提出的采用非均匀的B样条曲线解决了机器人准确经过多个中间插补位姿的难题，文献[3]中提出根据加速度约束，修正多项式最高阶次数，并利用修正后的高阶多项式进行轨迹规划改善了3-3-5-3-3多项式的平稳性。但是以上实验仍未解决中间的过渡点仍存在角加速度突变的问题。文献[4]中比较了三次多项式和五次多项式，证明了五次多项式在轨迹规划方面的平滑。文献[5]中提出采用五次多项式对于机械臂进行轨迹规划，能得到相对平滑的角位移、角速度、角加速度。但是五次多项式所构成的轨迹规划曲线与构成曲线的每个型值点都相关联，而B样条曲线的局部支撑性能有效的对轨迹规划后的曲线进行优化，只需改变相邻的几个型值点即可。文献[6]和文献[7]中分析了3-4-5多项式与五次非均匀曲线的优缺点，表明了五次非均匀B样条曲线在降低系统功耗和抑制机构残余振动方面具有显著优势。

针对于工业机器臂轨迹规划中，轨迹的平滑问题和机械系统的冲击问题，提出了一种新的轨迹规划的插值算法即“B-5-B算法”。并通过与“3-5-3算法”的对比仿真实验，表明了该算法提高了工业机械臂在运动过程中的角速度与角加速度曲线的平滑性，降低了角加速度突变引起的机械系统冲击力。

2 机械臂模型

在Adams/View中所建立的二连杆仿真模型，如图1所示。机械臂的模型主要包括了底座、大臂、小臂。其中大臂的长度为350mm，小臂的长度为295mm。在Adams中底座通过固定副与地面相连接，大臂通过旋转副与底座相连接，小臂通过旋转副与大臂相连接，并且定义底座与大臂之间的关节为关节1，大臂与小臂之间的关节为关节2，并在相应关节上建立的坐标系，如图1所示。底座的坐标系相对于全局坐标系绕Z轴逆时针旋转90°，关节1的坐标系与全局坐标系方向相同，关节2的坐标系相对于全局坐标系绕Z轴逆时针转动45°，在机械臂末端建立一个坐标系用于绘制运动轨迹，最后在底座和大臂的旋转副以及大臂和小臂的旋转副上设置驱动函数。同时设置测量函数，通过AZ、WZ、WDTZ函数分别设置底座坐标系与关节1坐标系绕Z轴方向的旋转角度、旋转角速度、旋转角加速度，作为为大臂的角位移、角速度、角加速度。设置关节1坐标系与关节2坐标系绕Z轴的旋转角度、旋转角速度、旋转角加速度，作为为小臂的角位移、角速度、角加速度。由于在关节1和关节2处添加有驱动函数，所以不需要再添加测量关节1和关节2处的力矩函数。

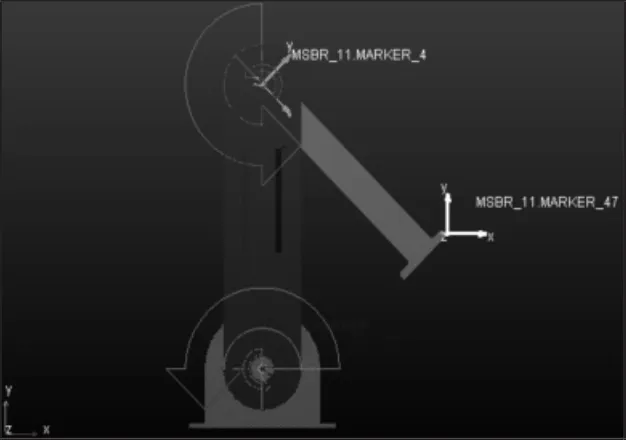
图1 样机模型Fig.1 Prototype Model

3 B-5-B轨迹规划

3.1 B样条曲线概述

假设有一系列的控制顶点 P1、P2、P3、…、Pn+1，则 K 阶（K-1 次）的B样条的函数表达式为：

式中：θj（t）—第j-1段的角位移；Pi—第i-1个控制顶点；Ni，k（t）—第i-1个K阶B样条的基函数；n+1—控制顶点数。

B样条基函数是一个称为节点矢量的非递减的参数t的序列所决定的K阶分段多项式，其表达式为：

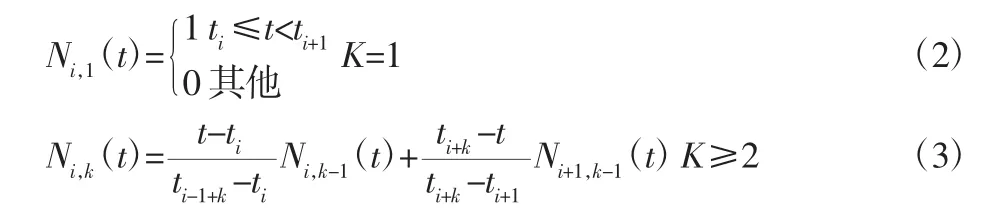
由式（3）表明，计算第i个（K-1）次B样条基函数Ni，k（t）时，需要 t1、t2、t3…t1+k，共 K+1 个控制顶点。

3.2 五次B样条曲线

对于五次均匀B样条曲线，取K=6得到五次样条曲线关于时间t的函数式为：

由于在关节空间的轨迹规划中，已知的是实际轨迹上的型值点，而非控制顶点，所以需要在给定型值点的情况下求控制顶点，假设有一系列的型值点θ1、θ2、θ3…θm存在，则需要构造m-1条B样条曲线，需要m+4个基函数同时需要求解m+4个控制顶点。当型值点按实际轨迹进行排列时，对于第i条的B样条曲线，其起点都是第i个型值点，其终点都是第i+1个型值点，由此能得到m个已知方程，所以需要再补充4个约束条件，在五次B样条曲线中可以对起点的型值点和终点的型值点进行一阶导数、二阶导数、三阶导数的条件约束，而在这里设定初始点和结束点的角速度、角加速度均为0，可以得到：

由方程组（5）能确定唯一的一组控制顶点 P1、P2、P3…Pm+3、Pm+4。将求出的控制顶点代入式（4）中就能求出介于两型值点之间的五次B样条函数。

3.3 五次多项式

根据五次多项式的特点，需要确定6个约束条件，但是由于五次多项式是位于两条B样条曲线之间，为了保证角位移、角速度、角加速度在连接点的平滑和连续，所以五次多项式起点和终点的角位移、角速度、角加速度由B样条曲线以及连接点的位置决定。假设五次多项式运动的时间为t0到te，约束条件为：当位于时间t0时，五次多项式的角度、角速度以及角加速度的值取上一条B样条曲线的终点对应的值，取角度为θ0、角速度为θ˙0、角加速度为θ¨0，当位于时间te时，五次多项式的角度、角速度以及角加速度的值取下一条B样条曲线的起点对应的值，取角度为θe、角速度为θ˙e、角加速度为θ¨e。得到，如式（6）所示。

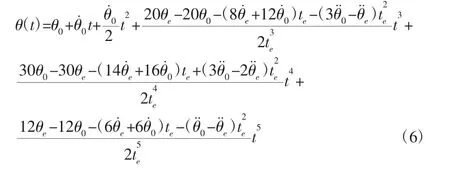
将实际的角度、角速度、角加速度代入上式（6）中可以得到用于B-5-B算法的过渡五次多项式的通用表达式。

4 ADAMS仿真对比试验

在Adams中采用二连杆模型进行轨迹规划，利用SOLIDWORKS建立模型，并给定关节空间中的对应时间和角度序列，如表1所示。

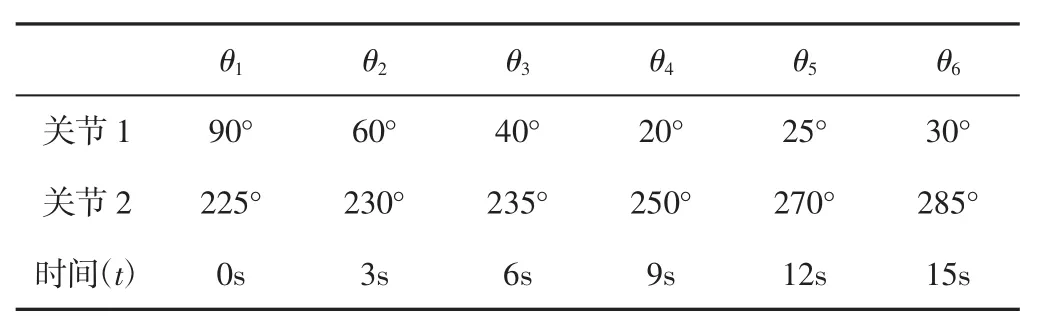
表1 时间和角度序列表Tab.1 Time and Angle Sequence Table

通过式（6）和式（16）可以求得五次B样条曲线的函数表达式以及过渡区域的五次多项式曲线的函数表达式，由于在五次B样条曲线中自变量t的值为（0，1），而对应的时间为0s到3s，为了使数据对应所以对数据进行处理，使得（0，3）能映射到（0，1）中，当进行了映射处理后，如果对角度函数式求导，将会发现角速度缩小了3倍，角角加速度缩小了9倍，同样的对3s到6s、9s到12s、12s到15s的B样条曲线和6s到9s的五次多项式曲线进行映射处理，将得到的关于时间的分段函数，通过IF语句分别输入到Adams中关节1和关节2中的MOTION驱动函数里，最后将Adams测量得到的角速度值扩大3倍，角加速度值扩大9倍，就能得到正确的数据。在二连杆末端设置一个MAKER点用于观察末端轨迹，如图2所示。从图中可以看出规划的曲线轨迹是平滑、无突变的，最后通过Adams/PostProcessor模块得到关节1和关节2的角位移、角速度、角加速度的曲线图，由于图幅限制，仅提供了关节1的B-5-B算法和3-5-3算法的角位移、角速度、角加速度以及力矩图的对比，如图3～图5所示。从关节1的角位移图中可以看出B-5-B算法和3-5-3算法，角度的起始点和终点都是一样，但是3-5-3算法中角度的起伏不大，并且一次下降或上升的幅度较大，将会由于惯性的缘故产生机械冲击问题，而B-5-B算法曲线的起伏较大，每次下降一定的幅度后，就会有上升的动作，从（6～9）s之间虽然两种算法都采用了五次多项式，但是明显的可以看出B-5-B算法中的五次多项式，更为平滑。曲线的变化更加小更平稳。

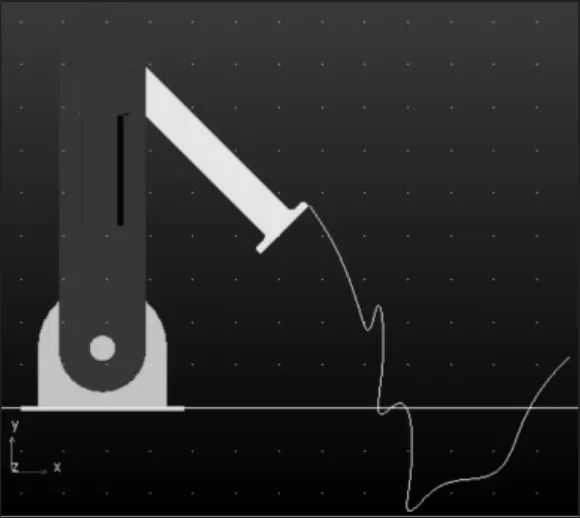
图2 末端轨迹图Fig.2 The End Trajectory

图3 关节1的角位移图Fig.3 The Angleof Joint One

图4 关节1的角速度图Fig.4 The Angular Velocityof Joint One

从关节1的角速度图中可以看出两种轨迹规划算法，在（0～15）s之间，B-5-B算法一共有8个峰值，表明了曲线变化得较快，3-5-3算法有5个峰值，变化较慢，但是可以明显的看出3-5-3算法的角速度曲线，在其中两个峰值处变化很快，容易导致角加速度突变产生机械冲击问题，而B-5-B算法虽然有8个峰值但是每个峰值处变化不大，不存在机械冲击的问题。

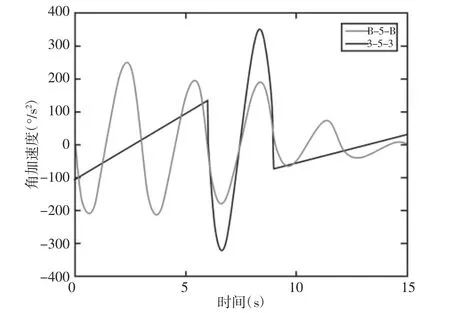
图5 关节1的角加速度图Fig.5 The Angular Acceleration of Joint One

从关节1的角加速度图可以看出，B-5-B算法的曲线起点是从0开始的，中间段拐角处没有突变，终点也是在0处结束的，整个曲线是平滑连续的，但是3-5-3算法的曲线起点是从-100开始的，表明了开始会有加速度的突变，并且中间段拐角处存在两个尖角，表明加速度变化很快，终点可以很明显看出3-5-3算法的曲线距角加速度为0，还存在一定的距离，所以终点也会产生角加速度的突变，以上三点都表明了3-5-3算法存在机械冲击。从关节1的力矩图，如图6所示。从图6中可以看出两种轨迹规划算法的曲线起点和终点都是一样的，起点的力不为0，是因为在Adams进行仿真实验中考虑了重力的缘故。从图中能够看出B-5-B算法是呈阶梯状下降，相对于3-5-3算法的曲线不易产生力矩冲击，并且在后半段B-5-B算法的曲线的起伏明显比3-5-3算法的曲线的起伏小，表明B-5-B算法比3-5-3算法在运动规划方面，更加的平稳，不易产生冲击。

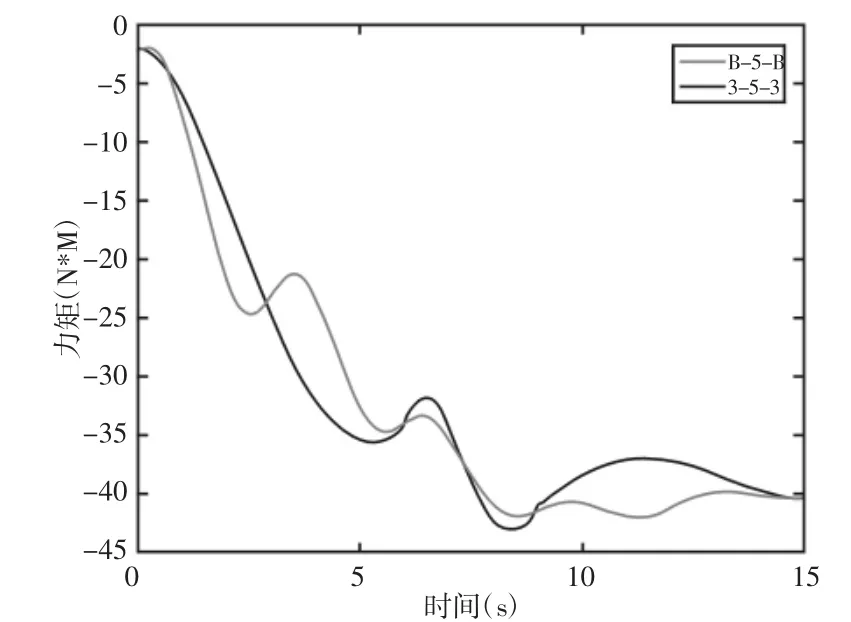
图6 关节1的力矩图Fig.6 The Momentof Joint One

5 结论

基于高次B样条曲线和高次多项式曲线，提出一种“B-5-B”轨迹规划算法。通过Adams的对比仿真实验验证了该算法在机械臂运动过程中的角位移图、角速度图、角加速度图、力矩图均光滑且连续，有效的避免了机械冲击，降低了虚拟样机所受的机械系统冲击力，由于采用五次B样条曲线所以在起始位置和终点位置能保证角速度和角加速度为零，也解决了“3-5-3算法”在起点和终点的角加速度存在突变的问题，在中间过渡曲线虽然和“3-5-3算法”都采用五次多项式，但是明显的“B-5-B算法”的曲线更为平稳。