正弦状非对称织构的动压润滑性能
2020-03-27傅连东湛从昌姜耀文
王 婷,傅连东,湛从昌,姜耀文
(武汉科技大学冶金装备及其控制教育部重点实验室机械传动与制造工程湖北省重点实验室,湖北 武汉 430081)
1 引言
润滑的目的是在摩擦表面之间形成润滑膜,用它来减少摩擦阻力和降低材料磨损。随着近年来的研究,表面织构作为一种可以显著改善表面摩擦学性能的方法,得到国内外学者的广泛关注,成为当前摩擦学领域热点研究方向之一[1-2]。20世纪60年代,文献[3-4]提出动压润滑理论,认为在材料表面加工出一些微凸体能够产生额外的承载力。现如今表面织构现已广泛的应用于机械密封、汽车发动机、轴承等方面。
表面织构的研究重点在织构的形貌,即凹坑类型:矩形、圆弧、三角形、梯形等,文章多论述最佳径深比,最佳面积率等[5]。表面织构的优化设计是大多数文献的研究重点,并在此方面已取得了一些的成果,但是这些研究仍缺乏综合性和系统性,尚未形成表面织构优化设计的完整理论[6-7]。目前表面织构的研究大多都基于简单对称织构,上述矩形、圆弧、三角形、梯形等微凹坑形貌都为对称结构,在往复运动中表现出相同的动压效应。选取非对称型织构进行研究,分析了其动压润滑特性、形貌与压力分布的特点。
2 织构模型的建立
2.1 几何模型的建立
如图1所示,为简化研究,选取单个织构进行分析。微凹坑几何模型,如图1(a)所示。织构的左右两面设置为周期边界,在此条件下,左右边界压力值、流体各点方向和流速等参数完全相同。上下两表面设置为壁面条件,其中下壁面固定不动,上壁面以速度U向右平行移动。模型整体长度为L,开有凹槽织构的部分的织构区长度为l,非织构区高度为油液入口高度h0,织构深度为d。非对称织构几何模型,如图1(b)所示。其参数与微凹坑织构类似,下表面织构形貌的函数方程为正弦函数:
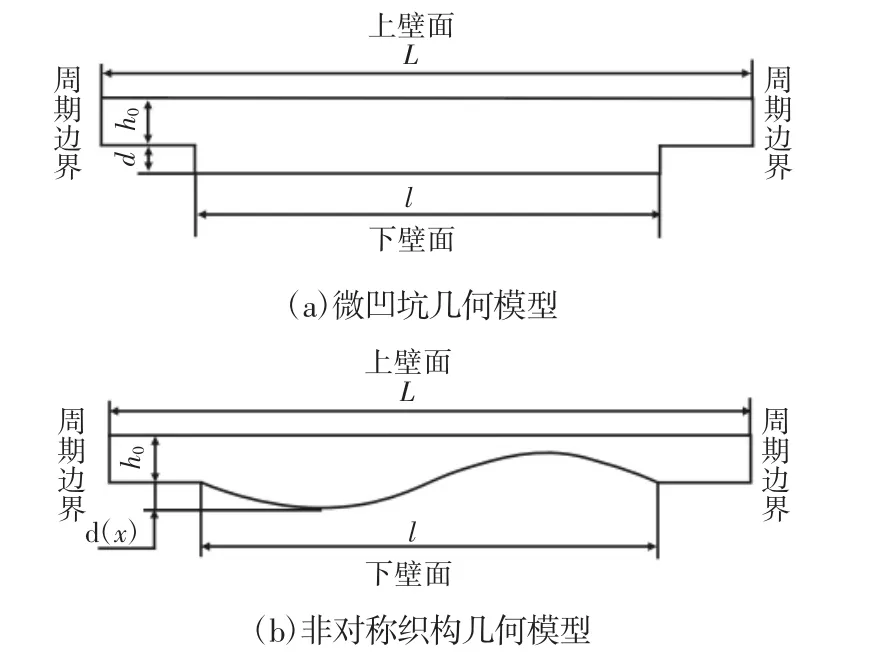
图1 织构的几何模型Fig.1 Geometrical Models of Textures
2.2 织构主要参数与控制方程
2.2.1 不可压缩流体的Reynolds方程
根据润滑油膜的形成原理和特征,润滑状态可分为:流体动压润滑,流体静压润滑,弹性流体动压润滑,薄膜润滑,边界润滑,干摩擦状态。上述织构润滑状态为流体动压润滑,现对模型做出以下几个基本假设:忽略油液的体积力;流体在界面上对壁面无相对滑动;沿润滑油膜厚度方向不计压力的变化;润滑剂是牛顿流体;忽略惯性力的影响。则由运动方程和连续性方程可以推导出不可压缩流体的Reynolds方程一般形式:
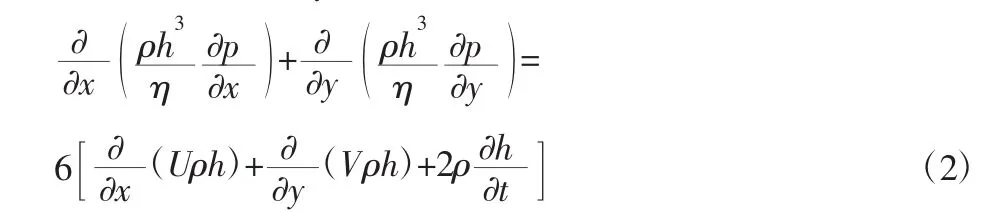
式中:ρ—润滑油密度;η—润滑油粘度;h—油膜厚度;P—油膜压力;U—织构上壁面运动速度;t—时间。
只考虑润滑膜压力形成的动压效应,则用于表面织构流体动压润滑计算的压力控制方程可简化如下:
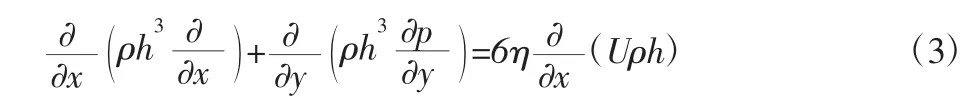
2.2.2 膜厚方程

式中:h0—未设织构表面油膜厚度;Ω—织构区域。
由织构模型可得x方向上任意点的润滑膜厚度
2.2.3 无量纲方程

式中:x,y—坐标向量。
则上式(3)、式(4)可化为:
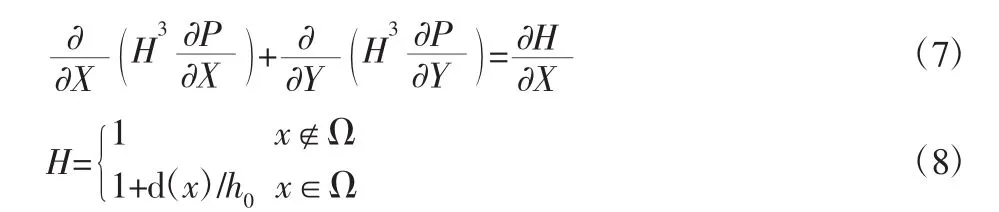
上述方程为雷诺方程的无量纲方程。
2.2 .4油膜承载力F的求解
在整个润滑油膜区域范围内润滑油膜的承载力,将压力P积分可得:

式中:F—承载力。
2.3 划分计算网格与定义边界条件
采用FLUENT软件对流场域求解。先用其前处理软件ICEM对表面织构进行网格划分。网格质量对数值模拟的精度与计算效率有相当重要的影响,为使得计算结果更加准确,选择对靠近边界处划分边界层网格。织构的上下表面都设定为“WALL”边界条件,其中上表面以速度U运动,下表面固定。左右两表面设置为周期边界条件。由于织构内部流体流动雷诺数较小,采用层流模型,CFD模型中的压力项则采用二阶中心差分格式,动量项采用QUICK差分格式进行差分,流体域的求解采用SIMPLEC算法。
3 仿真分析
3.1 非对称织构润滑效应分析
两种织构的压力分布的云图,如图2所示。可以看出两种织构都出现了明显的正压区和负压区。两织构计算条件都为上壁面以速度U向x轴正向运动。从图2(a)中可以看出,非对称织构在油膜厚度减小处出现了明显的正压,并产生了最大压力;在发散的处出现了明显的负压,产生了最小压力。以油膜最小处为分界点,左边区域形成正压区,右边形成负压区;在分界点处的压力急剧下降,压力数值从最大下降到最小。如图2(b),对称型凹坑织构在左边织构产生处出现发散区,产生负压;右边织构消失处出现收缩区,产生正压。在凹坑左边出现最小压力,凹坑右边产生最大压力,压力在整个织构区域内成缓慢上升趋势。
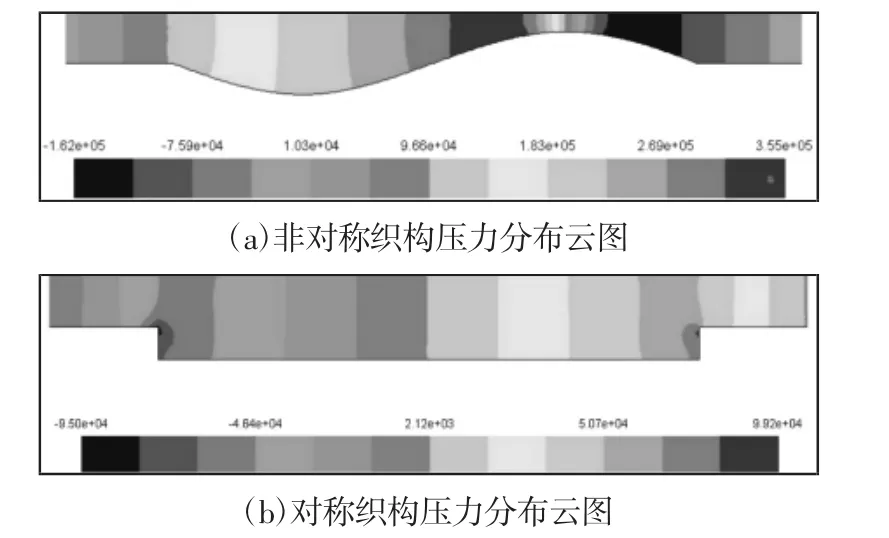
图2 织构压力分布云图Fig.2 Pressure Contours of the Textures
压力分布的曲线图,如图3所示。从中可见对称型凹坑压力分布图趋于对称,最大压力与最小压力绝对值相差较小,仅为4200Pa,正压区与负压区对比相差不明显,难以产生较好的动压润滑效应。而非对称织构压力分布呈的非对称性,压力值相差较大,最大压力与最小压力绝对值相差193000Pa,正压区与负压区差别明显,产生了较好的动压润滑效应。正弦状非对称织构在其波峰处与上壁面形成了更加微小的距离,得到一个最小油膜厚度hmin;对称织构的最小油膜厚度为h0,即为织构入口高度;在数值上hmin<h0。从整个织构区域上看正弦状非对称织构的油膜厚度值h(x)变化更大,因此能产生更好的动压润滑特性。
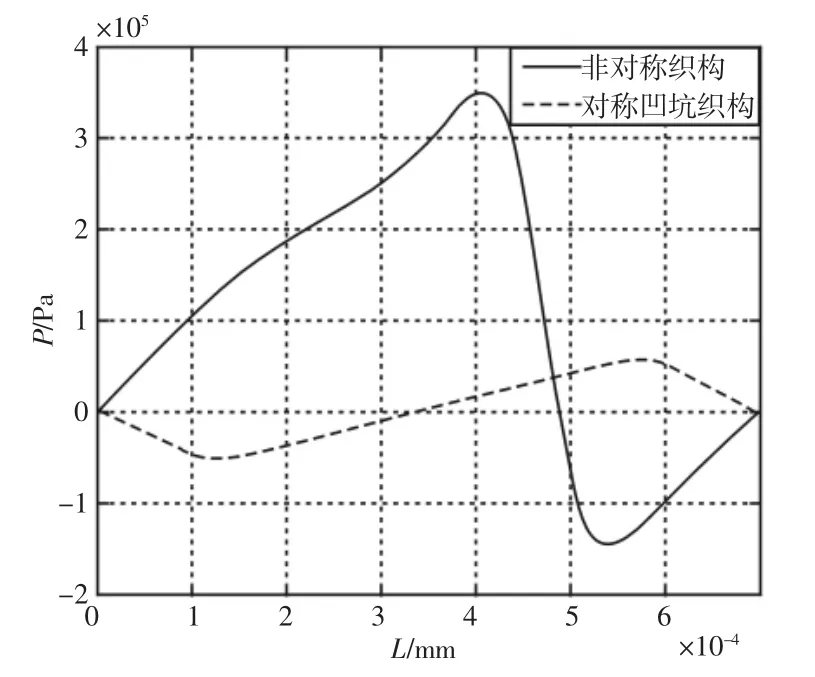
图3 织构压力分布Fig.3 The Pressure of Textures
3.2 影响非对称织构润滑性能的因素
3.2.1 表面形貌对织构承载力的影响
从上述分析可得,正弦状非对称织构在波峰处产生最小油膜厚度,且在相同范围内油膜厚度变化比凹坑织构大,动压润滑效应更好。
现改变正弦状织构的结构来分析动压润滑性能。用正弦函数y=Asin(ωx+θ)为典型织构表面形貌来分析非对称织构的动压效应。以上述图 1(b)织构为参考,形貌公式 d(x)=-30sin(πx/250)中A=-30,现改变正弦函数中A的值来改变织构的表面形貌。A=0时上下壁面都为平面,在水平方向上油膜厚度没有变化,不能产生动压润滑,其压力分布应为一条与x轴重合的直线。分别取A=-30 的倍数为 1,0.8,0.2,-0.2,0.8,-1 作出,如图 4 所示。速度方向一定时,织构区域内优先出现发散区,然后出现挤压时的结构动压润滑性能较好。在此结构中幅值较大的结构从发散区到挤压区压力的差值较大,变化更加明显。上述所有织构都在油膜厚度最小处发生了压力的急剧下降;油膜厚度越小,压力下降速度越快、越明显,压力差值也越大。正弦函数中幅值A为相反数的织构其结构特征为中心对称,压力分布图也成中心对称。
3.2.2 雷诺数的变化对织构承载力的影响
通过改变织构上表面运动速度U来改变雷诺数。对上表面的速度分别为 U=1m/s,2m/s,3m/s,5m/s,10m/s计算,如图 5 所示。
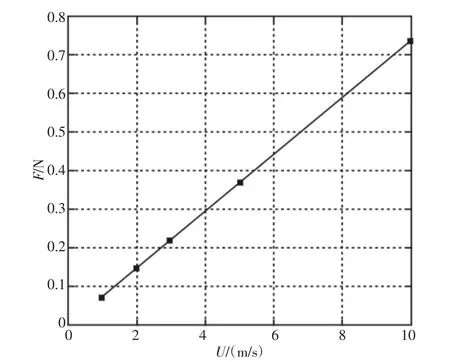
图5 速度对承载力的影响Fig.5 The Influence of Speed on Bearing Capacity
非对称织构形状固定时,承载力与速度成线性关系,并且随着速度增加,承载力也增大。
3.2.3 运动方向对织构承载力的影响
对称型织构由于其结构特征,在往复运动中会产生相同的动压润滑性能。为考虑非对称织构上表面的运动方向对其动压润滑效应的影响,选取图1(b)的织构进行分析得到的曲线,如图6所示。
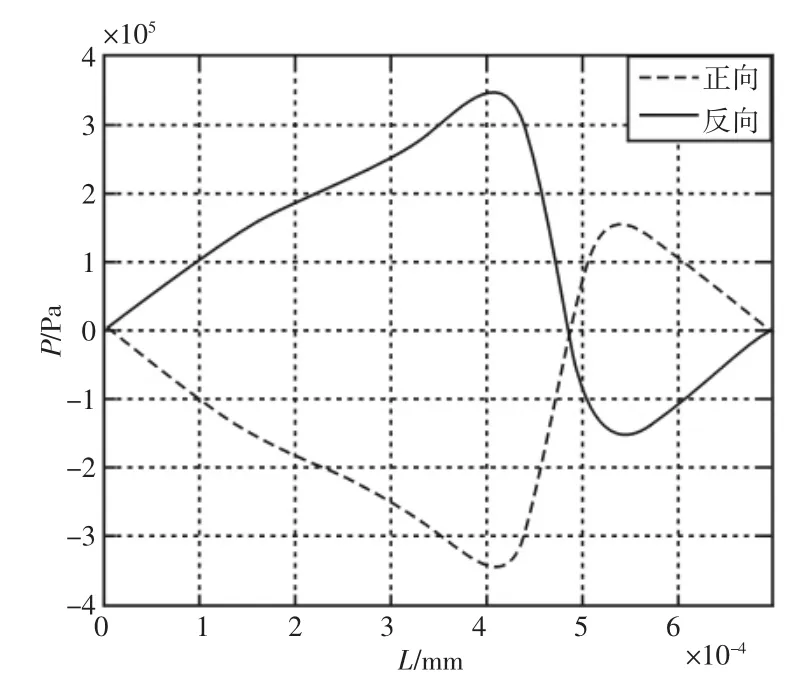
图6 不同方向下非对称织构的承载力Fig.6 The Bearing Capacity of the Asymmetric Texture Under Different Direction
其中,实线为上表面向x轴正方向运动的曲线,虚线为上表面向x轴负方向运动的曲线,两条曲线关于x轴对称。非对称织构在上表面运动方向相反时压力曲线关于x轴对称。正方向运动时产生的动压润滑效果比反方向好。
4 结论
非对称型织构在一定的条件下比对称凹坑织构有更好的动压润滑性能。这里正弦状织构,润滑油在由上表面带动下,先经过发散区再到收缩区的形貌产生正压;相反则产生负压。波峰与上表面最小距离hnim越小的形貌能产生更好的动压润滑特性。
非对称织构形状固定时,承载力与速度成线性关系,并且随着速度增加,承载力也增大。织构上表面的运动方向对非对称织构动压润滑性能影响较大。对于单向运动的情况,非对称织构比凹坑织构更合适。
