压气机效率测量与不确定度分析
2020-03-27
(西安工业大学机电工程学院 陕西 西安 710021)
引言
涡轮增压器是提高发动机功率密度,减少废气排放和燃料消耗的关键部件,已经被越来越多的企业采用[1]。涡轮增压器的关键部件是压气机。理想的涡轮增压器压气机满足包装尺寸、鲁棒性和成本的要求,同时以低惯性和高效率输送压力[2]。因为涡轮增压器压气机效率提高一两个百分点,可以区分产品,相关行业正进行大量投资,以改善经济效益。因此,对压气机的性能进行了实验测试评估,取得了较高的精度很有必要。
等熵压缩评价是典型的压气机性能评估方法,原因在于作出如下假设,比热容、气体类型和传热对压气机效率的影响比例非常低,设仅为0.01%,以至于可忽略,导致该模型计算简单,易于检测分析。然而真实的情况是,绝热的压缩条件是不存在的,也就是非绝热条件下的压气机效率高精度测量,往往需要对传热等因素进行假设分析才能获得可靠的结果。
本实验平台的涡轮增压器压气机是单级的,基于ASME 规范,完成对数据的采集。传统的效率计算方法忽略了传热[1]、动态流动条件和流动不均匀性[3]的影响。尽管有文献[4]已开展许多工作,但测量误差和不确定性往往被评估得很差。本文主要依据相对标准不确定度来进行该试验平台的高精度压气机效率测量,并就传热对压气机效率的影响进行预测分析,量化传热影响比例,为该实验平台的进一步研究奠定基础,该方法同样适用于其它压气机在不同场合的性能评估。
1 压气机效率的不确定度方程
对于绝热条件,压气机等熵效率被定义为等熵压缩过程的理想焓升与实际焓升的比值。表示为:


其中:T01和T02是压气机入口和出口温度,P01和P02为进出口压力,理想气体绝热指数k=1.4,Cp是定压比热容。
在实际压缩过程中,当气体在压缩过程中会产生大量的热,大部分热量留在气体中导致压缩后的气体温度升高,但仍有部分散到周围环境。仅依靠出口温度来确定出口焓值,显然是低估了实际功。因此,效率公式(2)的分母被低估,压气机效率被高估。这就需要对等熵效率公式进行适当的调整。则非绝热等熵效率可表示为:

其中:传热项q12表示单位气体质量与周围环境单位时间内的热量交换量。
等熵效率的不确定度源于压气机入口和出口处测量的压力和温度的不确定度,这些测量不确定度根据所采用的模型传播,得到等熵效率的最终不确定度[5]。考虑到热比r 恒定,等熵过程的理想出口温度不确定度方程:

等熵效率不确定度方程表示为:

2 误差来源分析
从各要素测量过程可以看出,压气机效率的测量受测量状态的影响。影响压气机性能参数的误差来源在不确定度分析之前必须清楚。Kline 和McClintock[7]指出,温度和压力在测量中存在5 大不确定因素:定位错误、安装误差、校准误差、设备误差及采集误差。实验中,前3 个因素被最小化,后2 个因素是测量系统误差,这些是由测量系统的每个组件引入的固定和可变误差,通常由制造商给出,如表1 所示为本实验所采用的具体型号。比热容和气体模型相互联系,已经在文献[6]有过讨论。涡轮增压器中的传热是一个非常复杂的现象,发生在三维领域,它受到涡轮增压器配置(如尺寸、冷却方法和材料)和周围环境的影响。从式(3)可以看出,本文把损失的焓都记作q12。这里实质分为3 部分:一部分是随空气排入管道,一部分是传递到了壳体及外部空气,第3 部分则是损耗在传动轴上。若忽略q12将得到错误的压气机效率值。因此,了解和准确地模拟压气机的传热至关重要,这可以改进实验特性和发动机性能预测。

表1 传感器的制造商规范
3 等熵效率测量实验与不确定度分析
图1 是本实验台的正面图,动力由压缩空气供应,将压缩空气输送到涡轮增压器的涡轮侧,涡轮机通过回转轴连接固连压气机,从而驱动压气机工作。使用的传感器已经过专业人员安装,通过软件采集得多组数据,取其中一组数据作为分析对象。

图1 实验平台
式(2)是表示等熵效率的实用方法,其等号右侧的所有参数都可以容易地被测量。假设测量的参数处于停滞状态,由压气机出入口处的温度和压力可直接估算压气机的效率。表2 是实验所测160 组数据中的5 组,按照传统方法计算得到其等熵效率。由式(5)和式(6),可计算得到各点的等熵效率不确定度,实验测量过程的等熵效率及其不确定度变化如图2 所示。
对比表2 中的1 组与3 组或者1 组与4 组,很明显可以看到压气机效率的测量受测量状态的影响。一般情况下,都会避免这种情况选择稳态区间数据。观察到第3 组、第4 组和第5 组,虽然都取自稳态区间,但其测量效率相对稳定但偏差仍较大。为解决该问题,就需要结合测量不确定度,合理对压气机数据进行数据选择和处理。依据不确定度的含义,波动范围越小说明越稳定。从图2 中可以看到,不确定度的波动范围,很明显在中后段趋近于稳定,这与计算结果一致,即从18 s 后,压气机等熵效率的不确定度为0.06。通过平均多组效率值可以减小随机误差对测量总误差的影响,故将稳态区间内的多组效率数据平均值作为压气机等熵效率的高精度测量值为88.86%,显然该数值包含了传热的影响,但仍然比传统单点计算精确一到两个百分点。

表2 传统等熵效率的计算结果
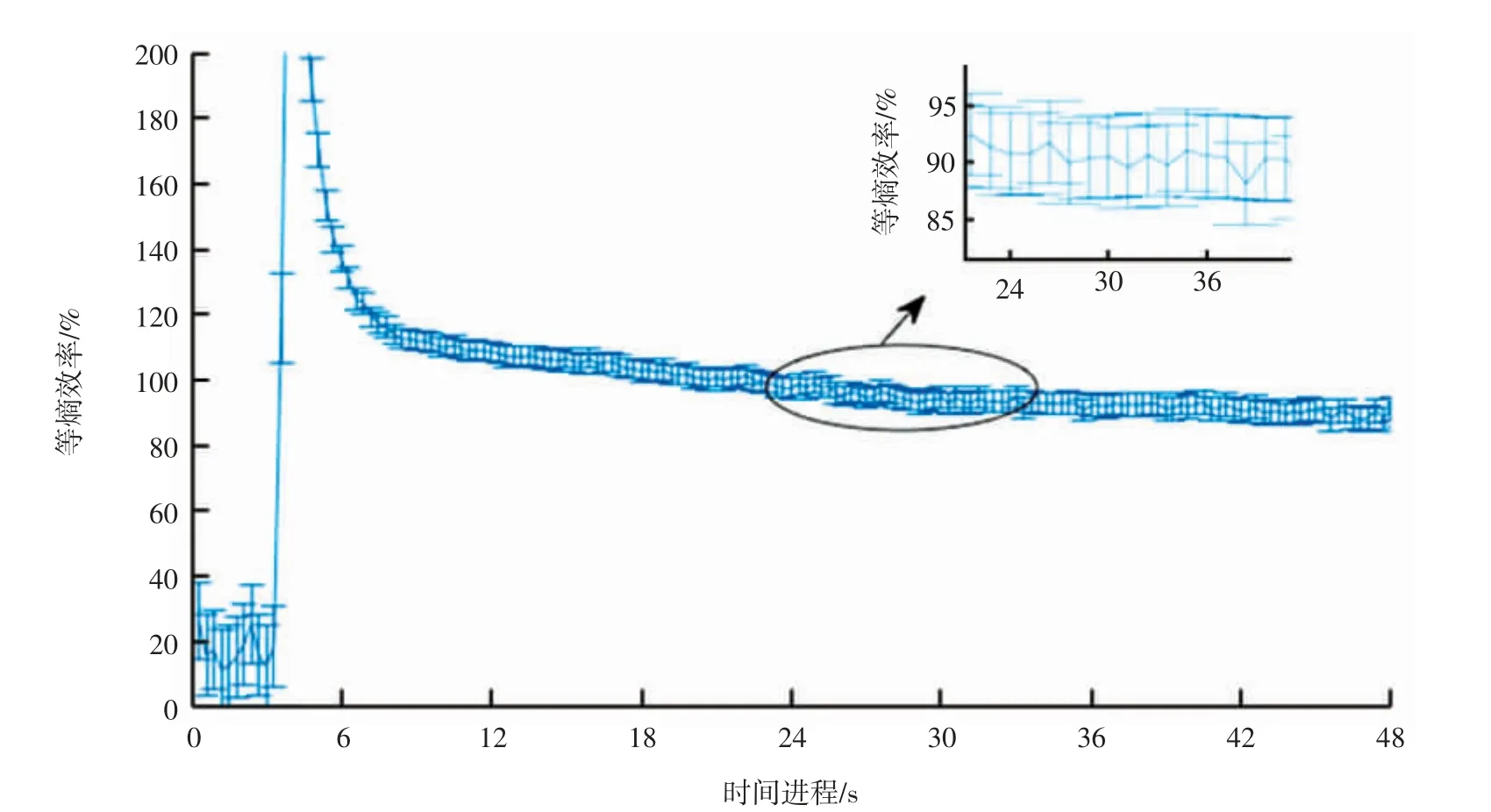
图2 压气机等熵效率不确定度变化图
4 热传导的影响预测分析
系统中的传热会影响涡轮机系统的进口和压气机出口流动温度测量。由于热传导,涡轮出口温度下降,可能会被错误地认为是焓的下降,从而导致错误的压气机性能评估和预测。本试验中的出口温度是未经过任何冷却装置,直接从压气机出口测量得到的。精确计算传热,就需要测得其损失部分的温度,显然是比较复杂和困难的,且该测量也仅限于实验室内,具有较大的局限性。事实上,我们用等熵效率损失的焓的特性来衡量压气机的性能。假定损失的热量为2 000 J/kg,得到图3 所示的等熵效率对比图。

图3 等熵效率对比图
从图3 可以看出,随着涡轮增压器工作进程的进行,等熵效率都趋于稳定,但仍然存在于不确定度范围内。假设总的热损失q12为2 000 J/kg,易得到二者之间的效率差值。按照同样的方法得到图4 传热造成的效率损失,将热损失设为100 J/kg 和500 J/kg等,就会得到本试验台的热损失影响比例。图4 中效率平均误差是由等熵效率相对稳定区间得到的。可以看出,随着热损失的扩大,每1 000 J/kg 将导致压气机效率被错误扩大2.6 个百分点。

图4 传热造成的效率损失
5 结论
1)通过对现实验台的涡轮增压器压气机误差源分析,得到了该压气机等熵效率的高精度测量结果。
2)针对实际测量中不可忽略的传热影响,量化了其效率影响比例,进一步精确测量压缩机实际效率。
3)基于传热损失预测模型,通过大致的热损失估计就可以进一步精确测量压气机效率,也可根据该影响比例,合理假设传热损失是否达到绝热条件等熵效率的忽略标准。
