壁面催化条件对气动热环境的影响研究

李旭东，张 赋，史增民，王 欣

壁面催化条件对气动热环境的影响研究

李旭东1,2，张 赋1,2，史增民1,2，王 欣1,2

（1. 北京航天长征飞行器研究所，北京，100076；2. 高超声速飞行器防隔热与热控技术中心，北京，100076）

为考察再入过程中壁面催化效应对气动热环境的影响，针对高超声速热化学非平衡流动条件下不同壁面条件（全催化壁面/非催化壁面）对气动加热的影响规律展开了研究。基于热化学非平衡流动特征构造了数值算法，并通过激波-膨胀风洞中开展的高焓高超声速地面试验结果进行了验证，然后考察了不同飞行高度下和典型几何外形下不同壁面条件对气动热环境的影响并分析了其影响机制。研究结果表明在50 km的飞行高度上催化效应明显，此时全催化/非催化壁面条件下热流存在明显差异，这种差异随着高度降低而减小。

高超声速流动；真实气体效应；催化壁面；数值方法

0 引 言

飞行器再入地球或者进入火星大气层时面临非常复杂的流动环境，由于强激波压缩，激波层内气体温度急剧上升，高温引起气体分子振动能激发，产生离解甚至电离以及电子激发和辐射等一系列复杂的物理、化学现象[1]，而当气体高温离解后流动到具有催化能力的壁面时，已经离解的原子会重新复合成为分子而在壁面上释放出大量的化学热，导致壁面加热量上升。当前飞行器飞行时间越来越长，如果不能准确评估壁面催化效应的影响将造成气动热环境预测精度偏差较大。长时间飞行下这种气动热预测偏差将导致防隔热系统设计方案偏保守，严重影响和制约了飞行器所能达到的水平。

本文以典型球锥外形——ELECTRE球锥为基础，通过多组分数值方法对不同飞行高度下催化/非催化壁面条件气动加热的影响和加热机理展开研究。

1 研究方法

1.1 数值方法

对于球锥这种简单外形的非平衡可压缩流动，国内外研究中一般采用多组分N-S方程[2,3]进行计算，本文针对壁面催化问题选用了5组分17基元反应模型。在零攻角情况下球锥流场是轴对称的，因此可以用二维轴对称方程来模拟。轴对称的N-S控制方程为

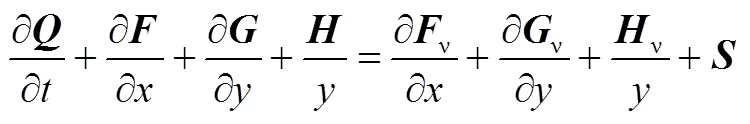
在计算中控制方程的离散采用基于密度的有限体积法。对流项的离散采用AUSMPW+格式[4]。该格式在高超声速的模拟中有广泛的应用，其计算量较小；而与矢通量分裂格式（Flux Vector Splitting，FVS）相比，耗散较低，对激波间断和边界层的捕捉有一定优势。本文应用该格式时，将通量分为对流项和压力通量项，根据马赫数来确定分裂的形式。在离散方程中离散界面通量通过左、右两侧的物理量来获得，但声速选择相同的值。时间积分采用隐式LU-SGS方法来加快收敛速度。

1.2 热化学反应模型

本文中化学反应模型选择Dung & Kang的高温空气化学反应模型[5]，用到其中5组分17基元反应模型，如表1所示。高温情况下流场中会出现振动能激发的现象，本文采用Park[6]的双温度模型，双温度模型的具体细节可以参阅文献[6]。

表1 Dung & Kang 高温空气化学反应模型

Tab.1 Dung & Kang's Reaction Model for High-temperature Air

序号反应方程式序号反应方程式 1O2+N=2O+N10N+N2=2N+N 2O2+NO=2O+NO11O2+O=2O+O 3N2+O=2N+O12O2+O2=2O+O2 4N2+NO=2N+NO13O2+N2=2O+N2 5N2+O2=2N+O214N2+N2=2N+N2 6NO+O2=N+O+O215NO+O=N+2O 7NO+N2=N+O+N216NO+N=O+2N 8O+NO=N+O217NO+NO=N+O+NO 9O+N2=N+NO——

在表1的反应体系中，非平衡流动下每个基元化学反应都可以朝着正、逆方向进行，但是正、逆反应速率都是独立的而不受平衡常数约束。正、逆反应速率均采用三系数的Arrhenius定律，其中的指前因子、温度系数和活化能，以及多组分下的输运系数（粘性系数、二元扩散系数等）均在文献[5]附表中列出。

1.3 数值方法的验证

本文采用＝25 mm的球头开展了多次试验，获取了试验气流条件下模型驻点的温度变化曲线以及热流曲线，并与本程序的计算结果进行了对比。地面试验在正向爆轰驱动激波-膨胀风洞JF-16E中展开，其结构如图1所示。该风洞利用正向爆轰大功率驱动技 术[7]，以及扩容环腔结构进一步改善驱动性能[8]，并应用高速运动激波在激波管-膨胀加速管内的非定常膨胀过程，实现高超声速试验气流。目前试验气流速度可在6~10 km/s之间自由选择。试验过程中首先在JF-16E开展了一系列典型模型的高超声速测热试验包括球头、尖楔和尖锥（如图1c所示）。通过上述试验表明试验设备具备产生离解气体的能力。

图1 JF-16E的爆轰驱激波-膨胀风洞以及典型模型试验（V∞=8.1 km/s）

本研究开展了3个典型试验状态的测热试验，试验状态分别为0=35、45、47 MJ/kg，试验件前来流条件如表2所示。

表2 来流条件

Tab.2 Inflow Condition

工况总焓/(MJ•kg-1)速度/(km•s-1)温度/K压力/Pa 1358.02390952.46 2458.92914607.95 3479.2950709.28

测热过程中使用了镍铬-康铜同轴热电偶传感器。同轴热电偶是基于热电效应的温度传感器，利用塞贝克效应将2种不同材料的导体或半导体A和B连接成一个闭合回路。结点的温度可以根据输出的电势确定，然后通过表面温度变化经过积分计算得到表面热流率，其直径为1.4 mm。在球头驻点中心打孔并安装传感器之后，热电偶与模型表面一起打磨抛光并镀铜膜导通内外2种材料构成回路；镀膜前后球头表面的变化如图1d所示。

计算中分别使用了全催化和非催化2种壁面化学模型，结果如表3所示。试验中测量得到了高达 37 MJ/m2的超高热流。对比结果表明，非催化壁面条件的计算结果与试验结果差别很大，而全催化壁面模型条件下的计算结果与试验结果吻合很好，在总焓 35 MJ/kg条件的两者差别小于10%，而总焓47 MJ/kg情况下两者差别接近17%。试验模型初期表面镀铜膜，可以认为是全催化壁面。通过上述对比结果可知，虽然数值方法直接给出热流数据比较困难，但仍然能处于合理区间内。

表3 JF-16E高超声速测热试验与计算数据对比

Tab.3 Comparison of Computation and Hypersonic Measurement on JF-16E

序号总焓MJ/kg测热试验热流MJ/m2Fay-Riddell公式数值计算热流 热流MJ/m2误差全催化MJ/m2误差非催化MJ/m2 13521.3922.203.8%23.178.3%10.05 221.921.3%5.7% 34532.5430.067.6%29.589.1%13.28 44737.3933.879.4%31.1016.8%14.23

2 壁面催化条件影响研究

2.1 典型外形与工况

计算模型外形选取ELECTRE头部缩比的球锥模型，头部半径为35 mm，总长为70 mm，锥角为4.6°，如图2a所示。计算中采用的网格为100×100，壁面处首层网格为0.001 mm，网格高度沿法向以1.05的比例递增，如图2b所示。

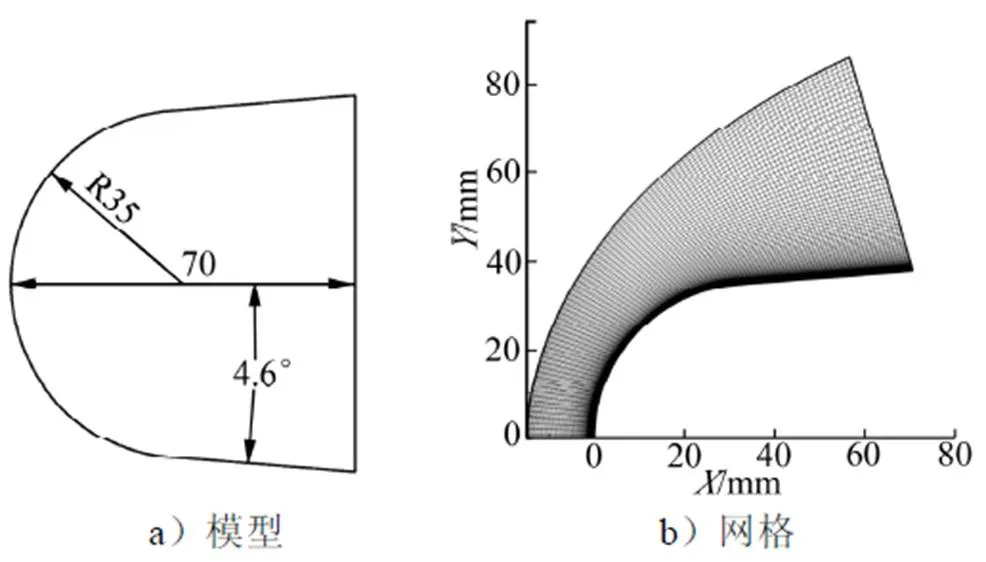
图2 球锥模型以及计算网格

2.2 40 km高空马赫数10~30气动热规律

来流条件选择40 km高空，飞行马赫数分别为10、20、25、30，计算得到模型壁面的热流分布如图3所示。从图3可以看出，模型头部驻点区域为热流峰值，沿着壁面向尾部热流逐渐减小，对于球锥模型，头部球形区域为主要的高热流区域，随着飞行马赫数提高，热流值变大。对比研究2种催化条件对热流的影响，=10时，2种催化条件得到的热流分布差别不明显，随着马赫数增加，2种催化条件差别逐渐增大，全催化高于非催化条件热流值。

图3 全催化&非催化条件下壁面热流分布

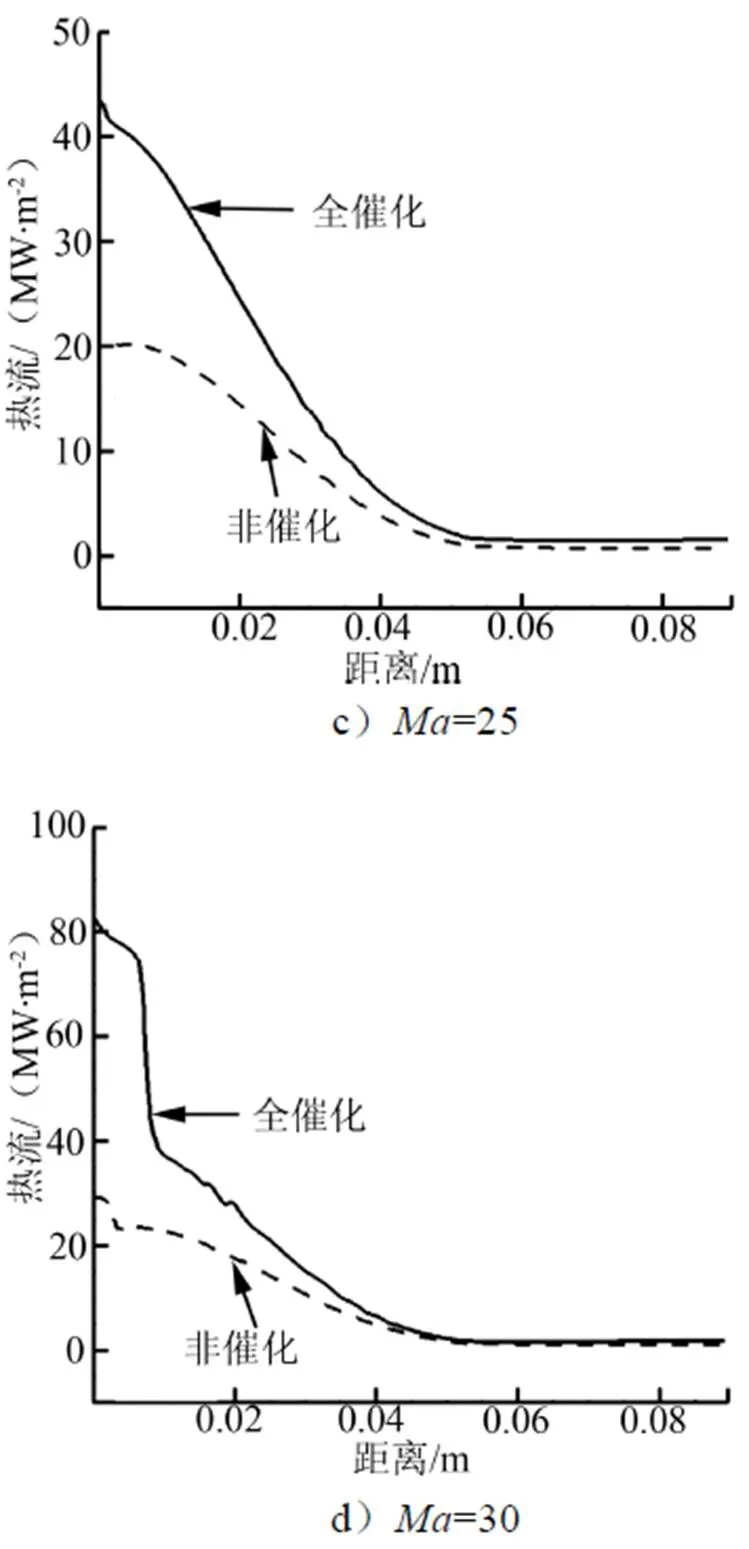
续图3

提取5组马赫数工况下驻点热流值，如图4所示。图4验证了之前的分析，在低马赫数时，2种催化条件下驻点热流率几乎重合，但在高马赫数时差异明显。

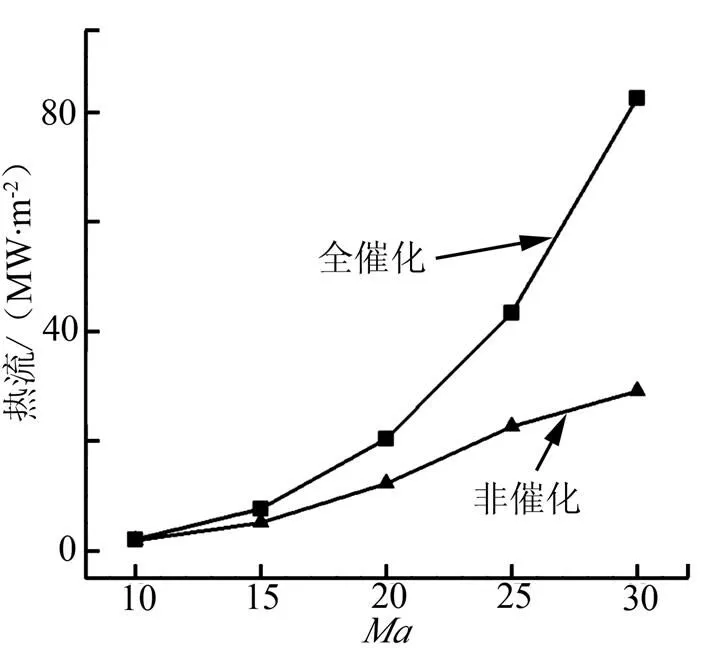
图4 Ma=10~30驻点热流

全催化与非催化条件下驻点热流的比值如图5所示。图5中，全催化条件在马赫数较高时，对壁面热流的影响有显著增加的效应，且随着马赫数不断提高，这种效应在加剧。分析原因认为，随着飞行马赫数的提高，头部激波的强度不断提高，导致波后气体离解程度加大，离解出的原子成分比重增加，造成壁面处有更多的原子进行催化复合释热，因此全催化条件的效应得到加强，对热流的提升也更为显著。

采用SPSS 22.0软件对数据进行分析处理，牙周袋探诊深度、临床附着水平、牙龈指数、牙齿松动度、牙槽骨高度等指标为计量资料，采用（±s）表示，满足正态分布和方差齐性后，组间相较采用独立t检验，以P＜0.05表示差异具有统计学意义。

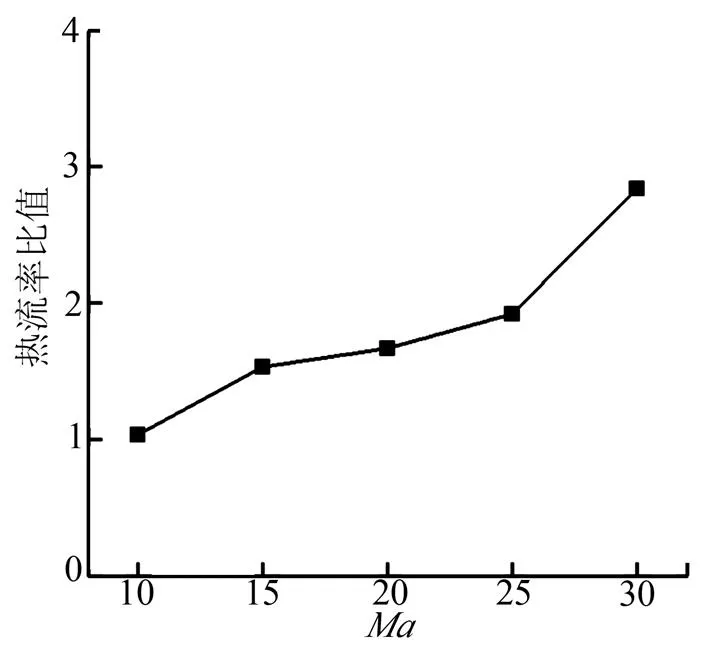
图5 驻点热流率比值（全催化/非催化）

提取=20时驻点线气流粒子质量分数分布，如图6所示。

图6 Ma=20驻点线组分质量分数

波后O2基本完全离解成O，N2也有较大的离解程度，在壁面附近，全催化条件下原子完全复合成分子状态，非催化条件则保留了一部分原子成分。表4为非催化条件驻点处粒子质量分数表。

表4 非催化条件驻点粒子质量分数表

Tab.4 Mass-fraction of Particles on Stagnant Point in Non-catalytic Condition

质量分数马赫数 1015202530 N20.76490.75690.69180.67090.6534 O20.22580.03250.02290.02230.0145 N0.00030.00630.07560.10690.1449 O0.00840.20180.20760.19740.1855 NO0.00060.00260.00210.00250.0016

由表4可以看出，马赫数较低时，离解效应微弱，因此壁面催化条件对热流的影响不大。随着马赫数提高，驻点处的原子质量比重增加，而相对应的全催化条件下原子质量比重为0，2种催化条件的差异在不断加大，催化效应对热流的影响随马赫数增加而加剧。

2.3 马赫数为20的40~70 km高空气动热规律

选择固定飞行马赫数20，来流条件分布选择 40 km、50 km、60 km、70 km高空气流参数，模型外形不变，研究不同高空气流参数对气动热的影响规律。

图7分别为高度为50 km、60 km、70 km时2种催化条件下壁面热流的结果，并加入2.2节中已经得到的40 km结果一起进行比较分析。

图7 全催化&非催化条件下壁面热流分布

由图7可以看出，随着飞行高度的增加，热流值减小。对比催化条件对热流的影响，70 km高空2种催化条件对热流的影响不大，壁面热流曲线几乎重合，但是在其余3组高度均表现出显著的差异。提取4组工况驻点热流如图8所示，并计算得到全催化对比非催化条件驻点热流比值如图9所示。

图8 40~80 km高空驻点热流

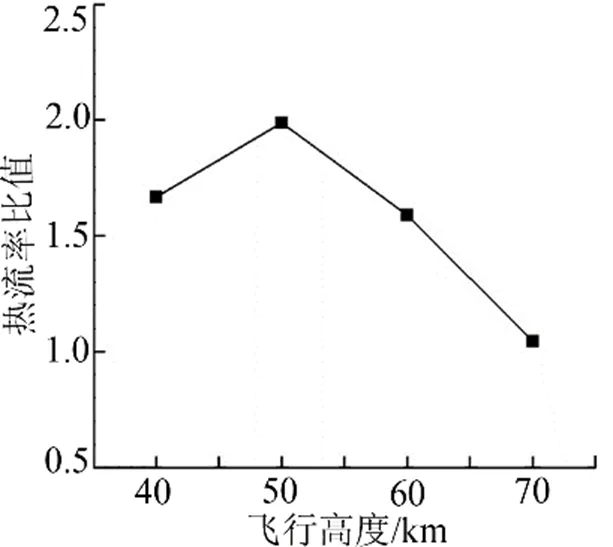
图9 驻点热流率比值（全催化/非催化）

由图8可知，随着飞行高度增加，2种催化条件驻点热流的绝对差值减小，在70 km高空处趋近于重合。图9中驻点热流的比值线出现一个拐点，40 km的值小于50 km，50 km高空以上该比值随高度增加递减。分析具体原因，提取50 km、70 km高空驻点线气流粒子组分质量分数，如图10所示。

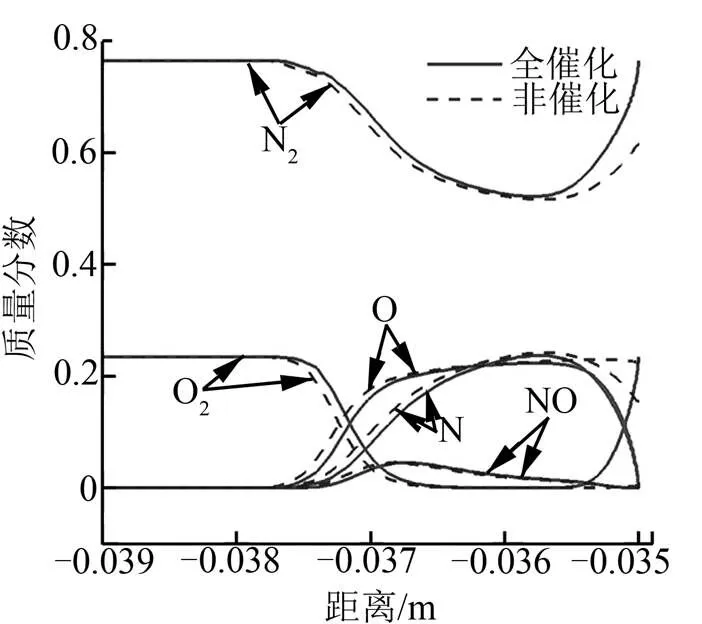
a）50 km

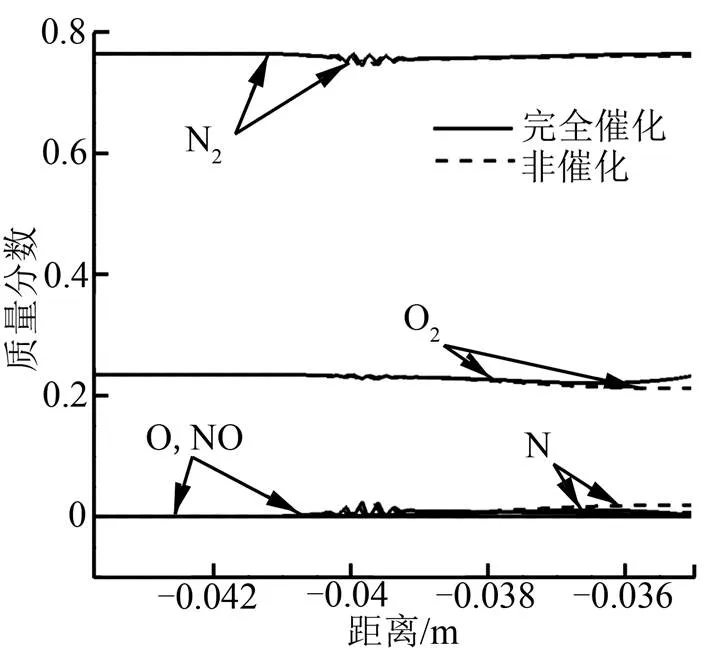
b）70 km

续图10

表5 非催化条件壁面粒子质量百分比表

Tab.5 Mass-fraction of Particles on Wall Surface in Non-catalytic Condition

质量分数高度/km 4050 60 70 N20.69180.61480.69250.7608 O20.02290.00400.00840.2124 N0.07560.15470.08180.0068 O0.20760.22450.21440.0188 NO0.00210.00200.00300.0011

从表5中可以看出，40 km原子组分质量比重小于50 km，50 km高空以上原子组分质量比重随高度增加而减小，验证了之前的分析。

3 结 论

本文首先利用地面试验开展小尺度模型高焓流动条件下的非平衡气动热测量，并验证了本文所用的数值算法。然后开展高超声速条件下全催化/非催化壁面的气动热环境影响研究，在研究中发现高焓条件下壁面催化条件对热流影响比较大。

a）在高马赫数下，激波后的分子离解更强，原子质量分数占比较高，因此在壁面复合的时候产生了较多的热流。

b）来流密度随高度减小导致在较高的高度上粒子碰撞不足，更多的原子运动到壁面时才复合，而低空中原子在流动过程中就得到足够的碰撞而复合。而当气体过于稀薄时（粒子碰撞数更少）导致分子离解很少，因此基本不受壁面条件影响。

[1] Bertin J J, Cummings R M. Critical hypersonic aerothermodynamics phenomena[J]. Annual Review of Fluid Mechanics, 2006(38): 129-157.

[2] 潘沙. 高超声速气动热数值模拟方法及大规模并行计算研究[D]. 长沙:国防科技大学, 2010.

Pan Sha. Hypersonic aerothermal numerical simulation method and massive parallel computation research[D]. Changsha: National University of Defense Technology, 2010.

[3] 李康, 等. 高焓热化学非平衡流动中再压缩效应对球锥气动力的影 响[J]. 力学学报, 2015, 47(2): 346-350.

Li Kang, et al. The effect of re-compression to aerodynamic force in hypersonic thermo-chemical nonequilibrium flow[J].Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(2): 346-350.

[4] Kim Kyu Hong, Kim Chongam, Rho Oh-Hyun. Methods for the accurate computations of hypersonic flows I[J]. AUSMPW+ SchemeJournal of Computational Physics, 2001(174): 38-80.

[5] Gnoffo P A, Gupta R N, Shinn J L. Conservation equations and physical models for hypersonic air flows in thermal and chemical nonequilibrium[R]. NASA TP-2867, 1989.

[6] Park C. Assessment of two-temperature kinetics model for dissociation and weakly-inozing nitrogen[J]. Journal of Thermophysics And Heat Transfer, 1988, 2(1): 8-16.

[7] 俞鸿儒, 赵伟. 氢氧爆轰驱动激波风洞性能[J]. 气动实验与测量控制, 1993, 7(3): 3, 38-42.

Yu Hongru, Zhao Wei. Performance of shock tunnel with H2-O2detonation driver[J].Aerodynamic Experiment and Measurement & Control, 1993, 7(3): 3, 38-42.

[8] 姜宗林, 等.长试验时间爆轰驱动激波风洞技术研究[J]. 力学学报, 2012, 44(5): 824-831.

Jiang Zonglin, et al. Approaches to extend the test time for Detonation-driven Shock Tunnel[J].Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(5): 824-831.

Research on the Influence and Mechanisms of Catalytic Wall Condition on Aerodynamic-Heating

Li Xu-dong1,2, Zhang Fu1,2, Shi Zeng-min1,2, Wang Xin1,2

（1. Beijing Institute of Space Long March Vehicle, Beijing, 100076; 2. Hypersonic Vehicle Research Center of Thermal Protection and Insulation, Beijing, 100076）

To investigate the influence of catalytic wall condition to aerodynamic-heating,the effects of different wall conditions (Fully catalytic wall/ Non-catalytic wall) on aerodynamic heating for hypersonic thermal-chemical non-equilibrium flow are studied. Numerical method, which is constructed according to the thermal-chemical non-equilibrium flow characteristics and verified by high enthalpy & hypersonic ground experiment results, are used to investigate the influence of different catalytic wall conditions on aerodynamic thermal environment and its intrinsic mechanism for some typical geometrical configurations and different flight heights. Study shows that there’s a significant catalytic effect when flight height is above 50km, and heat-flux under FCW/NCW differs apparently. But the difference between heat-flux und FCW/NCW reduces with flight altitude decreasing.

hypersonic flow; real-gas effect; catalytic wall; numerical method

TP333

A

1004-7182(2020)01-0112-06

10.7654/j.issn.1004-7182.20200120

2018-06-28；

2018-09-22

李旭东（1983-），男，博士，高级工程师，主要研究方向为高速化学反应流动与气动热。

张 赋（1992-），男，博士，工程师，主要研究方向为激波相互作用以及试验流体力学。

史增民（1970-），男，研究员，主要研究方向为气动热环境。

王 欣（1992-），男，工程师，主要研究方向为气动热环境。