基于AMESim和Simulink联合仿真的阀控马达转速控制

毛雨露

（长安大学工程机械学院，西安 710000）

0 引言

随着液压伺服技术的快速发展，阀控马达系统由于其响应频率高、控制精度准、调节时间短、动态性能好被广泛应用在工程机械领域，尤其是功率小、响应速度快的系统[1]。阀控马达速度控制系统中马达的转速控制是整个系统的核心，然而由于液压系统本身具有高度的非线性，且工程机械在大多情况下面临载荷大、工况复杂多变的情况，系统往往具有大迟滞性和时变性等特点，传统PID控制不能满足控制要求。为此，本文提出了基于参数自整定的模糊自适应PID控制理论来提高阀控马达系统的调速性能，并利用AMESim和Simulink软件进行了联合仿真[2]。

1 阀控马达速度控制系统

1.1 阀控马达速度控制系统的控制原理

本研究中的阀控马达速度控制系统的结构原理如图1所示。其中液压系统主要由三位四通电液比例阀、液压马达和负载3部分组成。

图1 阀控马达速度控制系统结构原理

本文研究的电液比例阀控马达系统的输入信号为期望转速转换成的电压信号Ur，将电压Ur与转速传感器转换成的马达实际转速电压Uf一起输入到比较器中得到偏差信号Ue，当偏差信号通过比例放大器放大后作为电液比例阀的输入信号，信号大小控制阀芯的开口大小，从而带动液压马达旋转，达到实时改变马达转速的目的[3]。

1.2 AMESim中系统模型建立及参数设置

根据实际需要，在AMESim中建立阀控马达系统的物理模型，设置系统和元件的仿真参数，并添加与MAT⁃LAB相连接的interface接口。创建的模型如图2所示。

图2 阀控马达系统AMESim模型

系统中主要元件的参数如表1所示。

表1 泵控马达调速系统的相关参数

系统通过接口模块将液压马达的转速信号传递到Simulink中，同时通过该模块输出MATLAB中的控制信号，从而控制电液比例阀的开口。

2 模糊PID控制器设计

2.1 模糊控制器结构的选择

模糊PID控制系统结构框图如图3所示，控制器选择2输入3输出的二维模糊控制器，以期望信号与实际测量信号的偏差e和偏差变化率ec作为输入，通过量化、模糊化、模糊推理和去模糊化4个过程，得到3个输出参数：比例系数变化量△Kp、积分系数变化量△Ki和微分系数变化量△Kd，然后通过系数变化量分别对PID的3个参数Kp、Ki、Kd进行在线整定，保证阀控马达速度控制系统具有良好的动态特性。

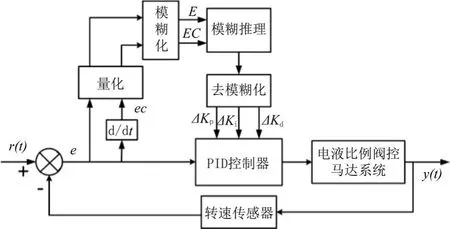
图3 模糊PID控制器结构框图

2.2 输入、输出模糊化与隶属函数的选择

设输入偏差e，偏差变化率ec的模糊论域为E、EC=[-3,3]，输出ΔKp的模糊论域为ΔKp=[-0.3,0.3]，ΔKi的模糊论域为ΔKi=[-0.06,0.06]，ΔKd的模糊论域为ΔKd=[-3,3]。根据实际情况，若输入和输出的实际论域为N=[A，B]，[A，B]不在E、EC的模糊论域范围内，则需要通过量化因子和比例因子将输入、输出量化到各自论域范围中，如表2所示。

表2 输入、输出变量模糊化表

将输入、输出量划分为7个模糊子集{NB，NM，NS，ZO，PS，PM，PB}，并为了方便起见，简记为{负大，负中，负小，零，正小，正中，正大}。隶属度函数的确定：Z型和S型隶属度函数分别用于左边界和右边界，中间选用三角形隶属度函数。输入、输出量的模糊隶属度函数定义如图4所示。

图4 隶属度函数曲线

2.3 建立模糊控制规则

模糊控制规则表是专家知识和现场操作员经验的结合，通过分析得到若干条模糊条件语句，使控制器按照实际需要实现参数的在线自调整[4-6]。

（1）当实际马达转速与期望值误差|e|较大时，应先输入较大的Kp，目的是为了使系统响应快速提升，同时需要对积分作用加以限制，防止偏差瞬时增大。

（2）当马达转速误差|e|为中等时，应取较小的Kp，防止系统具有较大的超调，并且保证系统有较快的响应速度。

（3）当马达转速误差|e|较小时，应取较大的Kp和Ki使系统的稳态性能更好。同时为了防止振荡出现在系统期望值附近，马达转速误差变化率|ec|也应当合理取值。

综上，制定模糊调整规则表三维响应曲面图如图5所示。

图5 模糊PID模糊控制规则表三维响应曲面图

3 AMESim与Simulink联合仿真

3.1 联合仿真方法

本文是在AMESim软件里搭建阀控马达系统的物理模型，然后在Simulink软件里搭建系统的控制模型。通过在AMESim软件中创建interface接口将阀控马达系统的转速信号输入到Simulink中，在仿真过程中，AMEsim将自动生成与存储文件名一致的动态链接文件，以S函数的方式存在。当在Simulink中创建控制模型时，调用S函数并输入控制器输出信号，运行后通过AMESim转速传感器可以观察系统的响应曲线[7]。

3.2 MATLAB/Simulink中建立联合仿真模型

将MATLAB/Simulink与AMESim的工作目录设置成相同的，在新建的Simulink中调用AMESim生成的S函数，并在S-function中设置参数[8]。

Simulink中搭建的自适应模糊PID控制系统封装后模型如图6所示。

图6 阀控马达模糊PID调速系统仿真模型

3.3 仿真结果及其分析

本文仿真设定如下：（1）液压马达转速的期望值为200r·min-1，并在5 s时施加反向负载；（2）系统跟踪周期1 s的正弦信号。

为了验证模糊自适应PID控制策略的优越性，对阀控马达系统分别进行了传统PID控制和模糊自适应PID控制仿真，并对仿真结果进行对比分析。

当对系统输入幅值为200的阶跃信号时，仿真结果如图7所示。通过对比图可以看出采用模糊自适应PID控制的系统响应速度更快，超调量更小，调节时间由1.5 s变为0.5 s。

图7 AMESim空载时阀控马达系统阶跃响应

系统稳定后，对两种控制系统在5 s时分别加入阶跃干扰，测试它们的鲁棒性。仿真结果如图8所示。可以明显看出：模糊自适应PID控制器加入扰动后恢复到期望转速所用时间少，且转速震荡更小。

图8 AMESim加载时阀控马达系统阶跃响应

在工程实际应用中阀控马达系统还需要研究追踪性能。对两种控制系统输入幅值200，频率为1 r/s的正弦信号，仿真结果如图9所示。通过图9可以看出采用模糊自适应PID控制下的正弦信号响应与输入信号几乎完全重合，幅值超调减小，相角滞后减小，跟随性能高，系统的跟随性能有很大的改善。

图9 AMESim阀控马达系统空载正弦信号响应

4 结束语

本文通过AMESim和Simulink联合仿真建立了阀控马达速度控制系统数学模型，解决Matlab使用传递函数单一仿真的不精确性。同时分别采用了传统PID控制和模糊自适应PID控制策略对液压马达转速进行控制，通过结果对比图发现，模糊自适应PID控制下的系统有更好的动态性能，系统的响应速度明显提高，超调量减小，抗干扰能力提高，跟随性能更好，其鲁棒性优于传统PID控制器。