基于SLP和粒子群算法的车间布局优化研究*

徐晓鸣，邓裕琪，吴绮萍

（1.广东海洋大学机械与动力工程学院，广东湛江 524088；2.深圳市三一联光智能设备股份有限公司，广东深圳 518106）

0 引言

随着全球经济一体化进程加快，以及当前社会经济存在下行风险，企业面临提升核心竞争力的压力与挑战，合理的车间布局，能减少企业在制品库存，提高空间利用率，降低生产成本[1]。因此，采用合理高效的车间布局方法对企业提高效率势在必行。

车间设施布局问题实质上是一种组合优化问题，当布局的设备数量越多，求解越困难，至此国内外学者在该类问题求解进行了大量的研究。文献[2]针对车间布局问题构建了各作业单位总物流强度最小和物流成本最小双目标模型，并运用遗传算法进行求解，并验证了算法的有效性。文献[3]结合传统SLP方法，构建了物流总成本最小模型，并运用遗传算法进行求解，验证了算法的有效性。文献[4]针对于车间布局问题构建了物流搬运总成本最小模型，并运用粒子群算法进行求解。文献[5]构建了一个混合整数规划模型，并运用切平面法进行求解，得出最优布局。上述文献从不同的角度建立车间布局优化目标函数，然而从搬运物流成本最小和各作业单位间的非物流关系密切程度最大的多目标考虑不足。

本文在传统SLP方法基础上，构建了物料搬运成本最小和非物流关系密切程度最大目标规划模型，借助粒子群算法对模型优化求解，结合实际情况对求得的结果进行调整，得出最优的布局方案。通过以SY公司为研究案例，对比前后布局方案的物料搬运成本和非物流关系密切程度，验证方法的有效性。

1 车间布局问题建模

1.1 假设与参数

生产车间的设施布局问题是一个组合问题，各作业单位的面积尺寸不相同，车间的可利用面积有限，在建模时需要做以下假设：

（1）假设需要布局的设备结构均为矩形，长度和宽度均为可知，随机摆放且平行于四周空间。

（2）各作业单位均为矩形，作业单位的长、宽尺寸和所需的面积均可求，各作业单位的中心点在同一水平线上。

（3）物料的运输路线与车间的长度和宽度平行，且不考虑使用不同搬运工具产生的搬运不同费用，即单位搬运成本一致。

建模参数设计如下。

X为长度方向，Y为宽度方向，L为车间的总长，W为车间的总宽；Fi、Fj、Fk、FN为车间内第 i、j、k…N 个作业单位，共有N个作业单位；xj为作业单位Fj在X轴的中心坐标；yk为作业单位Fk在Y轴的中心坐标；li为作业单位Fi的长度；wi为作业单位Fi的宽度，m；dxik为作业单位Fi和作业单位Fk之间在X轴方向的最小距离，m；dyij为作业单位Fi和作业单位Fj之间在Y轴方向的最小距离，m；loj、woj分别为作业单位Fj距离Y轴和X轴的最小距离；dij为作业单位Fi和作业单位Fj的曼哈顿距离，m；cij为作业单位i到作业单位j之间的单位搬运成本，元/kg

·m；qij为作业单位i到作业单位j之间的年平均物流量，kg；dmax为生产车间总规划区域的长与宽之和；Tij为作业单位i与作业单位j之间的非物流关系值，根据密切程度等级进行量化，如表1所示；bij为作业单位i与作业单位j之间的接近程度，称为关系因子或关联度，由dij转化得到，如表2所示。

表1 作业单位间的密切程度量化表

表2 关系因子的确定

1.2 目标函数

车间设施布局以车间搬运成本（Z1）最低、作业单位间非物流关系密切程度（Z2）最大为车间布局模型的双目标函数。

其中i和j为作业单位的编号，且i≠j。

将双目标函数转化为单一目标函数。

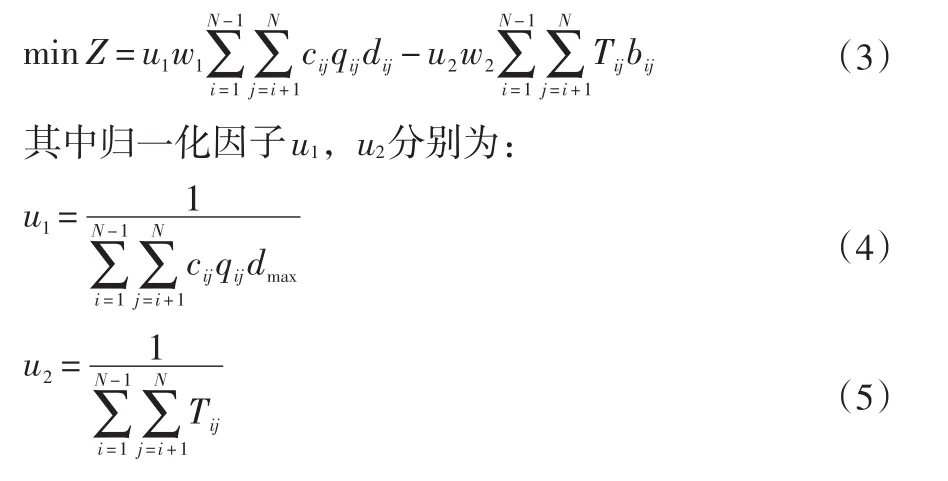
w1表示物料搬运成本的权重，w2表示非流关系密切程度的权重，且w1+w2=1。

1.3 约束条件

（1）间距约束

间距约束是指作业单位之间要留有适当的安全距离，作业单位不能重叠摆放。则间距约束可表示为：

（2）边界约束

车间的长和宽是一定的，各作业单位的总长和总宽应小于待布局车间的总长和总宽，且作业单位与车间的四壁应留有一定的距离。则边界约束可表示为：

（3）固定约束

车间布局过程中，对一些特殊的设备和作业单位要单独进行考虑，例如锻造和电镀等特殊单元一般都安排在角落，而有些作业单位的位置因为建筑结构等问题具有固定的位置，在布局时不能随意变动，可以将这些比较特殊的作业单位区域固定下来，在布局设计时不在其中布置别的作业单位，设Dk为固定区域，则固定约束可以表示为：

2 基于粒子群算法求解

2.1 编码设计

假设待布局车间有N个待布局作业单位，每个车间布局方案对应为一个粒子，则每个粒子的位置和速度都为2N维向量。每个粒子的位置向量前N维标识作业单位坐标在X轴上的投影，后N个维标识作业单位坐标在Y轴上的投影；每个粒子的速度向量前N维标识在X轴上的投影，后N维标识在Y轴上的投影。具体的位置P和速度V在2N维度上的坐标如下式。

算法优化过程中主要通过追踪Pbest和Gbest两极值，在解空间中进行搜索，每个粒子按式（16）～（19）进行更新。

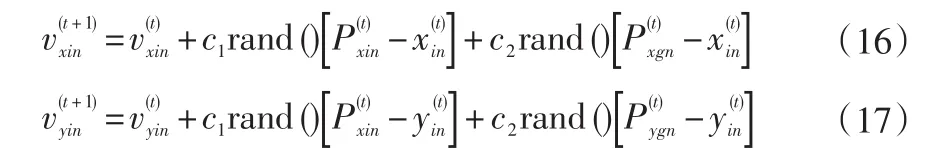
式中：t为迭代次数；c1、c2为非负常数，称为加速系数；rand（）为均匀分布在（0，1）的随机数；为第t次迭代时N维空间中的第i个粒子在X轴坐标上经过的最好位置；为第t次迭代时N维空间中的第i个粒子在Y轴坐标上经过的最好位置；为第t次迭代时N维空间中的粒子群在X轴坐标上经过的最好全局位置；为第t次迭代时N维空间中的粒子群在Y轴坐标上经过的最好全局位置；为下一轮迭代时，N维空间中的第i个粒子，在X轴上的投影；为下一轮迭代时，N维空间中的第i个粒子，在Y轴上的投影；n=（1，2，…，N），n表示N维空间中的第n个变量。

2.2 参数设计

（1）加速系数的确定

合理设置加速系数的取值，可以减少算法陷入局部极值中的概率，通常取c1=c2，且c1+c2≤4，根据经验，一般取值在[0.5，2]之间能够取得较好的优化结果。

（2）适应度函数

为保证适应度函数为非负，将目标函数做如下处理：

式中：Max为一足够大的常数。

3 案例应用

3.1 案例概况

SY公司是一家专门从事SMD编带机、贴片测试分类机、外观检测机等智能设备的生产，属于中小型企业，按订单组织生产。根据SY公司车间的生产设备状况，结合辅助部门，按照功能相似性原则划分出作业单位，划分为12个区域，为别为：（1）来料存放区；（2）机加工区；（3）装配区；（4）检验区；（5）物料存放区；（6）组装区；（7）仓库；（8）生产多料区；（9）IQC；（10）杂物间；（11）成品区；（12）滞销设备存放区。

表3 作业单位面积设计值

拟布局的车间长175 m，宽120 m，各作业单位所占面积各作业单位所需面积如表3所示。

作业单位原坐标向量为：

X=[30 21.6 45 42 40 60 84 80 108 19 23 78]；

Y=[38 10 45 40 35 50 60 40 6 15 43 35]

3.2 物流分析

根据划分的作业单位，对各作业单位间的年物料搬运量进行统计分析，得到各作业单位间的年物流量从至表，如表4所示。

表4 作业单位间物流量从至表

3.3 非物流分析

根据SY公司设备生产的特点，制定各作业单位间相互密切程度理由，如表5所示。在此基础上做非物流作业单位相互关系图，如图1所示。

表5 各作业单位关系密切程度理由

3.4 优化过程和参数设计

在本案例中，运输成本c=0.01元/(kg·m)，dmax=295，Max=1 000，u1=1.3×10-7，u2=0.023 3。在实际中，SY公司没有特殊的加工区域和需要固定的区域，因此不考虑固定约束。

为保证粒子群算法的优化效果，选取五种具有代表性的加速系数，分别运行1 000次，选取每种加速系数较优的3次结果进行对比。因为适应度值为目标函数的倒数，为使目标函数值最小，适应度值要选取最大的。不同的加速系数的对比分析如表6所示。

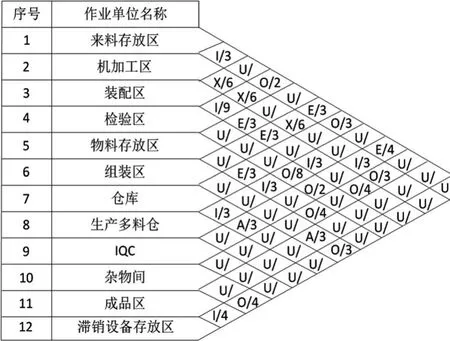
图1 非物流作业单位相互关系图

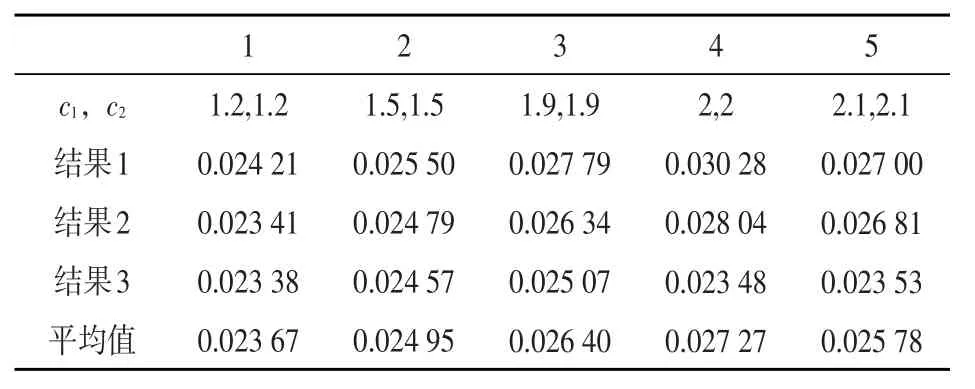
表6 加速系数对比分析

由表6可知，c1=c2=2时的适应度值平均值最大，即目标函数值最小，此时的优化结果为5个方案里的最优方案，运行求解过程如图2所示。根据求解结果，获得单个作业单位的坐标位置如表7所示。

图2 运行过程

理想状态下的布局图，考虑到实际布局的空间外形等限制条件，结合SY公司的车间建筑结构情况，对优化结果进行调整，得到最终的优化布局方案如图3所示。

3.5 有效性分析

对SY公司生产车间原布局经过分析，给定作业单位原布局相应的坐标，代入算法中进行求解，再与优化后的值进行对比，优化前后方案对比如表8所示。

SY公司在改善前，物料搬运成本过高，导致产品的总体成本随之升高，产品的市场竞争力相对较弱。通过布局改善后，降低了搬运成本，各作业单位之间的协作沟通也更加密切，生产管理就会更加顺畅，因此，得出的优化方案有一定的可行性。

表7 X，Y坐标求解结果

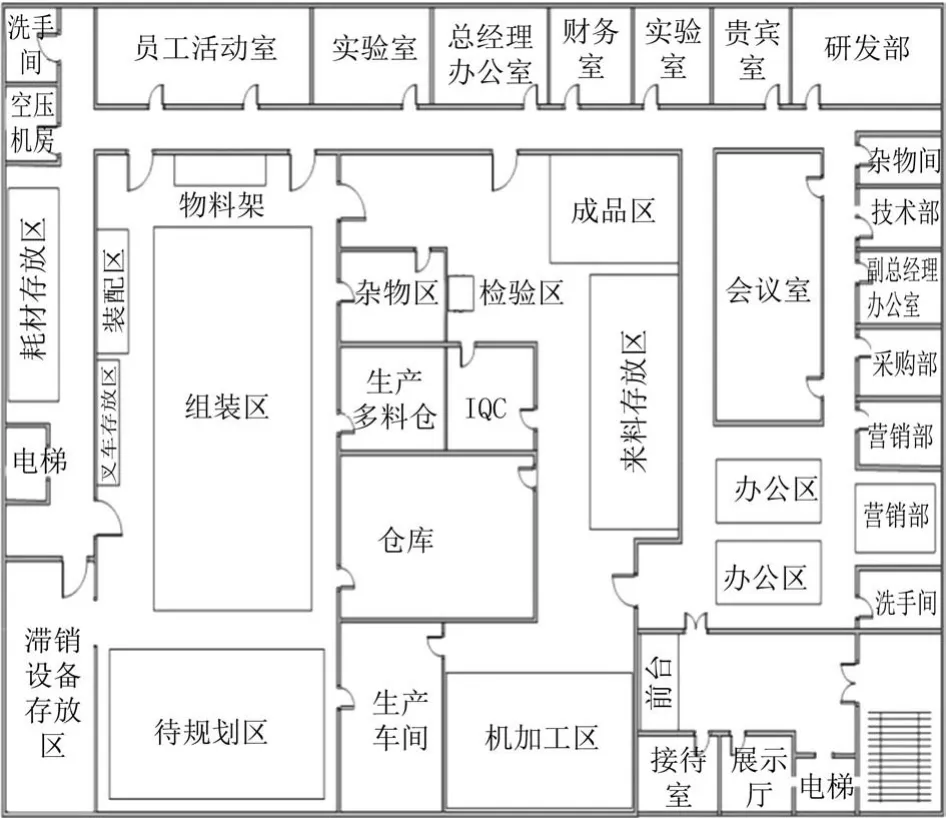
图3 最终布局方案

表8 方案对比分析

4 结束语

本文以SY公司的生产车间为例，对车间的现有布局进行了分析，找出现有布局问题的所在点。利用SLP方法进行车间布局的分析，对车间进行了作业单位的划分，分析各作业单位间的物流量和非物流关系，对车间布局问题进行建模，以物流成本最小和非物流关系最大为双目标进行分析求解，通过粒子群算法，最后得出优化的布局方案。通过优化前后布局方案的对比，验证了优化后得车间布局方案可行，对SY公司车间布局改进具有一定的指导意义。

通过本文的研究与应用，运用SLP方法和粒子群算法能够有效的解决企业布局问题，为相关企业解决布局问题提供了一种有效途径。