基于X光图像的芯片在线自适应计数算法研究
2020-03-26雷臻宇贺香华骆佩文谢德芳
雷臻宇,贺香华,骆佩文,周 聪,谢德芳
(广州大学机械与电气工程学院,广州 510006)
0 引言
芯片技术的不断发展和进步,其性能越来越高,在各领域的使用越来越广泛[1-3]。芯片在出厂前一般使用料盘的形式进行包装,芯片装入卷带再缠绕在料盘里,如图1所示。芯片价格昂贵,出厂前需要对每个料盘内芯片数目进行准确计数,但每个料盘内芯片数量少则几千,多则几万个,且单个芯片体积非常小,无法使用人工进行计数,需要有稳定可靠的解决方案完成整盘芯片的快速自动计数工作。近年来,机器视觉技术以其快速、稳定、可靠的性能,在工农业生产中的尺寸测量、缺陷检测和自动计数等领域得到了较广泛的应用。机器视觉技术可用于对农作物计数,评估生产量、优化管理[4-6];对图像细胞进行计数,用于医学诊断[7];甚至利用图像对运动物体进行计数等[8]。利用机器视觉在芯片计数领域,目前还没有找到相关文献。
图2为通过使用X光在料盘垂直方向拍照获取的料盘图像,图3为芯片部分局部放大的图像。使用图像对产品进行计数,一般是首先设定产品的模板图像,然后使用模板匹配的方法在图像中搜索匹配到与模板类似的对象,从而实现产品的计数[9-10]。但针对芯片计数的应用,使用模版匹配的方法存在以下几个问题:(1)芯片型号众多且切换频繁,每次切换型号都需停机重新制作模版,降低设备使用效率;(2)每张图片中,芯片数量众多,全部使用模版匹配耗时较长;(3)芯片包装紧密,有些相邻芯片在图像中粘连在一起,会对匹配造成较大干扰,影响最终计数结果的精度。

图1 芯片包装料盘
为了解决以上问题,本文提出基于X光图像的芯片在线自适应计数算法,可根据不同芯片产品的图像信息自动调整相关参数;对于图像中芯片相互粘连的问题,通过自动估算单个芯片的大小,即使紧密粘连在一起的芯片也可以大致估算出相应的数目。
1 算法流程
结合实际生产需求,本算法需要满足以下条件:(1)针对不同类型芯片图像,算法无需人工干预,可自动调整相关参数;(2)偏差率小于0.3%;(3)单张图片耗时小于3 s。
算法流程如图3所示。本算法主要分为以下几个步骤:
(1)读取芯片的X光图像;
(2)自动提取芯片感兴趣区域:首先去除滚筒区域的干扰,然后为降低背景区域污渍的影响,利用自动阈值提取卷带区域,最后在卷带区域里利用自动阈值提取出芯片区域;
(3)估算单个芯片面积,并计算芯片总数;
(4)输出结果。

图3 算法流程图
2 芯片区域自动分割
2.1 图像预处理
首先统计出芯片料盘图像的灰度直方图,如图4所示。结合图2芯片料盘图像,芯片、滚筒、卷带和背景区域分别分布在相应的波峰带。因此,在各波峰带做阈值分割,即可提取相应区域。图4中,滚筒区域峰值与芯片区域峰值相隔不明显,会影响对芯片区域提取的效果,因此需从原图中去除滚筒区域。

图4 灰度直方图
由于芯片被包装缠绕在同种规格的料盘上,因此滚筒区域的灰度值范围基本一致,采用固定阈值分割,对滚筒区域进行自动提取屏蔽。

式中,i,j分别对应图像中第i行,j列。 f(i,j)、 g(i,j)分别对应阈值分割前后对应点的灰度值,m1、m2为阈值。
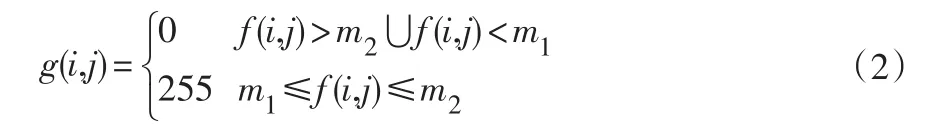
对滚筒区域做阈值分割,取m1=0,m2=80,分割后的结果如图5所示。
对分割后的区域采用最大面积特征提取[11],提取结果即为滚筒区域。从图5可以看出,滚筒区域边缘部分并没有被完全提取出来,因此对滚筒区域做膨胀运算。膨胀后的区域再与原图做补集运算,得到去除滚筒区域B,如图6所示,此时滚筒区域已被去除,图像记为S。

图5 滚筒区域分割结果

图6 去除滚筒区域B
补集运算如图7所示,A区域与B区域构成集合U,对A区域做补集运算得到B。

2.2 芯片区域分割
由于个别图像上存在着污渍、噪声干扰且污渍灰度值与芯片灰度值接近,如图8所示,直接提取芯片区域会一并将污渍提取出来,影响计数结果。为减少污渍干扰,先提取出卷带区域,在卷带区域的背景下提取芯片区域。
不同芯片卷带区域的灰度峰值范围不同,大小也不同,所以基于固定阈值分割的方式对卷带区域进行提取是不稳定的,效果也不理想。对此,本文提出一种自动阈值方法,能根据不同芯片图像的区域信息自动调整相应阈值。
首先统计出S的灰度直方图,直方图经过高斯函数(σ=1.5)平滑[11]后如图9所示。
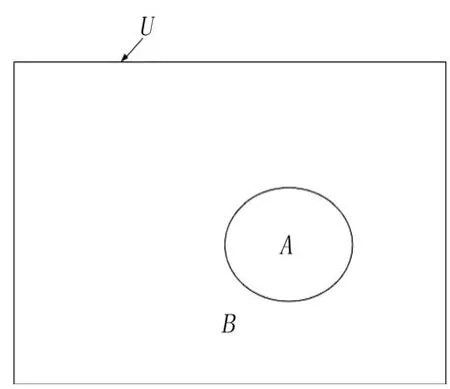
图7 补集运算

图8 带污渍的图像

图9 灰度直方图
然后找出直方图上的波峰波谷。将灰度直方图看成函数f(x),x∈[0,255]∩x∈N的函数图,定义波峰波谷为函数的极大、极小值(个别波峰由于峰值太小,直方图上体现不明显)。对此函数定义:如果存在点x0的某一邻域[x0-1,x0+1],使得对任意x∈[x0-1,x0+1],都有f(x0) >f(x),则称x0为f(x)的极大值点,f(x0)为极大值。同理,极小值为对任意x∈[x0-1,x0+1],都有f(x0) <f(x)。经高斯平滑后,灰度值会产生细微波动,造成了f(x)<1的极大值点,为排除此影响,选出的极大值需大于50。若临界值f(0)>f(1),f(255)>f(254),则x=0,x=255为极大值点。统计出所有波峰点xn(n=1,2,3…且x1<x2<x3…<xn)。
最后在灰度直方图上,取后2个波峰即xn和xn-12个函数点间的极小值作为阈值m2,m1取0对S2进行阈值分割,对分割后的区域作最大区域面积特征提取,提取结果即为卷带区域。在做最大区域面积提取后,卷带区域边缘可能会有损失,如图10所示。因此在提取最大区域面积前应对分割区域作膨胀运算。
卷带区域提取后,在卷带区域背景下做自动阈值提取芯片区域。
同样的,首先统计出卷带区域的灰度直方图,用高斯函数平滑(σ=1.5),如图11所示。

图10 卷带区域提取结果
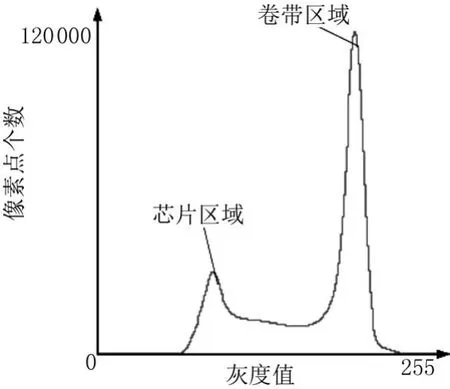
图11 灰度直方图
取前2个波峰x1和x22个函数点间的极小值作为阈值m2,m1取0。对分割后的区域做面积特征提取,提取面积大于等于5像素的区域,此时区域可认为是芯片区域,如图12所示。

图12 芯片区域提取结果
芯片的提取区域用“+”标志。在统计结果发现,个别图像芯片与卷带灰度差异不明显,难以完全分割提取出来,如图13所示。因此利用增强对比度的方法,增加芯片边缘区域灰度差异后再进行阈值分割。

图13 增强对比度前后比较
增强对比度:首先对S进行均值滤波[11],掩滤波器大小为7×7。然后对滤波后的图像做如下处理:

式中,ori是原始灰度值,mean是滤波后的灰度值,Fac作为增强对比度的度量,round()把实数四舍五入转化为整数,取Fac=1。
3 自动计数
3.1 单个芯片面积估算
如图14所示,提取后的芯片区域还存在以下问题:(1)图14(a)存在多个粘连区域,有2个、3个甚至更多芯片区域粘连在一起;(2)图14(b)图像上的污渍被提取出来产生干扰(噪声区域);(3)图14(c)污渍与芯片一起形成粘连区域。

图14 误差来源
由于图像上的芯片精细且分布紧密,很难有方法分割出单个芯片区域而不影响其他区域。为此,本文提出基于连通区域面积的计数方法。
首先对提取出的芯片区域面积做概率统计,如图15所示。面积出现次数最多的即为单个芯片的标准面积s1。由于单个芯片面积小且占绝大多数,为提高算法速度,只需0~400像素范围内的区域面积做概率统计。

图15 面积统计图

图16 倍数统计图
3.2 倍数关系调整结果
然后针对这些噪声、粘连区域设置相应的倍数关系来减少误差,提高精度。用600张图片作为测试集,测试倍数与实际个数之间的关系,如图16所示。
针对图16倍数关系交界区域做误差统计,最终得出如表1所示的倍数关系。

表1 芯片区域划分
最后芯片总数为:
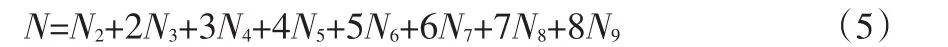
4 实验与分析
4.1 实验步骤
选择配置为CPU Intel Core i5 2.5GHZ,内存8G的PC测试算法。实验数据为500张不同的芯片图像,几种代表性芯片图像的提取结果如图17所示。测试步骤如下:
(1)用模板匹配方法进行计数,对匹配结果用“+”标记,统计出漏标多标的误差数量,实际数量z;
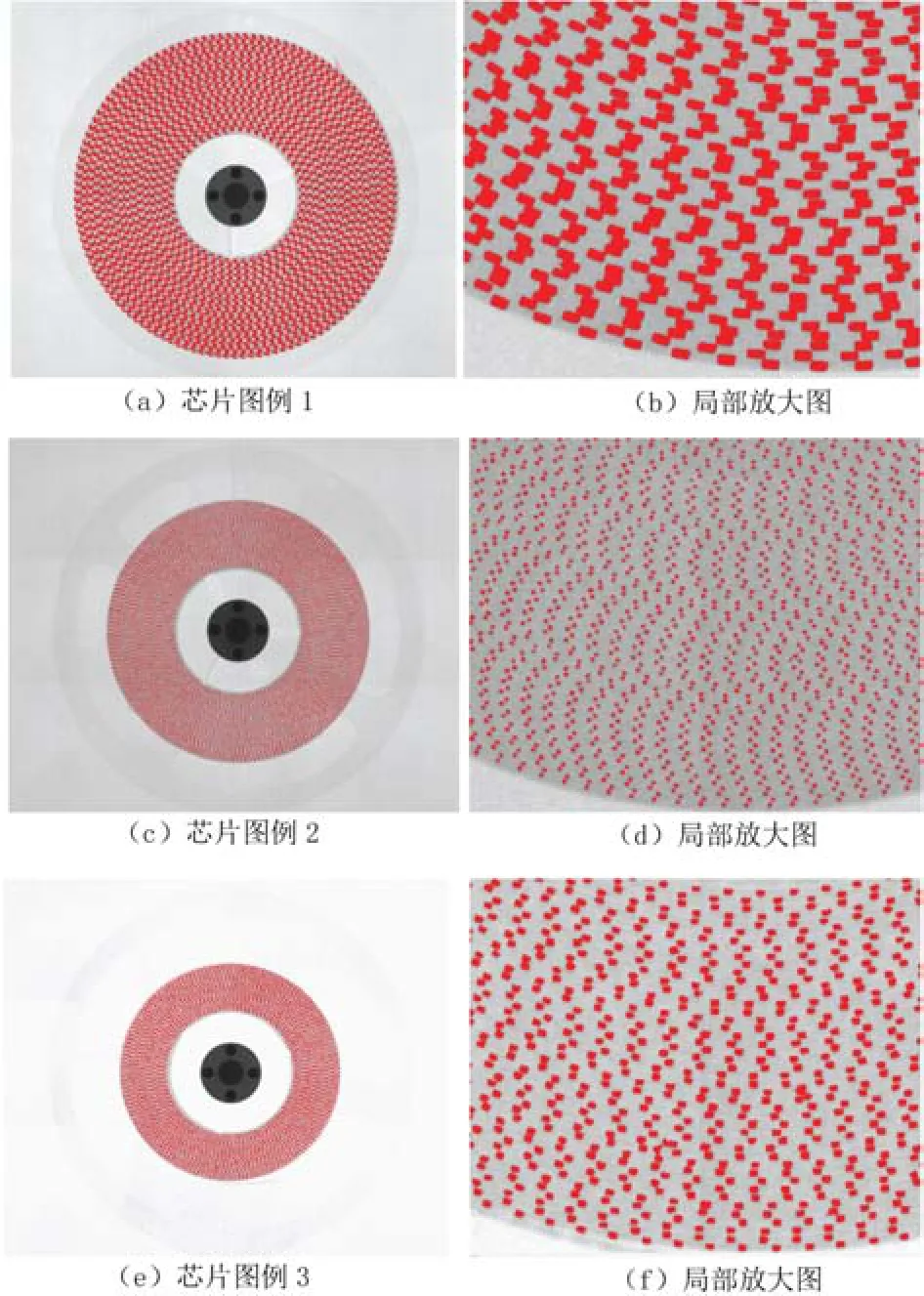
图17 不同芯片图像举例
(2)设置好倍数关系,利用本文算法对500张图片自动计数;
(3)汇总实验结果,计算各自偏差率。
4.2 结果分析
将2种方法的计数结果汇总:统计出算法的平均偏差率y,平均耗时。xi表示单个图片的偏差数,zi表示单个图片的实际数量。

实验结果如表2所示。

表2 实验结果
从表2可知,模板匹配方法不仅需要频繁切换模板,而且偏差较高,耗时长。而本文算法不仅能做到根据图像自适应调整相关参数,而且通过对粘连区域设立倍数关系,大大改善了偏差率。偏差率平均为0.03%,平均耗时2.9 s/张(图像分辨率为3 072×2 592),满足实际需求。
5 结束语
本文提出一种基于X光图像的芯片在线自适应计数算法,该方法基于自动阈值,实现了相关参数的自动调整,通过设置单个芯片参考面积和倍数关系,解决了芯片粘连紧密的问题。实验表明,最终平均误差为0.03%,耗时平均为2.9s/张(图像分辨率为3 072×2 592),能达到生产线上的自动化要求,有较高的实用价值。如何分割芯片与污渍粘连的区域,是下一步需要深入研究的问题。
