双定子风力发电机齿槽转矩的削弱研究*
2020-03-26刘志华许志伟许智萌
刘志华,许志伟,许智萌
(1.风力发电机组及控制湖南省重点实验室,湖南湘潭 411104;2.湖南省风电装备与电能变换协同创新中心,湖南湘潭 411104)
0 引言
随着国民经济的发展,我国的能源消费量和需求量越来越大。目前,我国的能源消费结构以不可再生的化石能源为主,但煤、石油等化石能源不仅会对环境造成严重的污染,而且单一的能源结构不利于我国的能源安全战略[1]。我国的风能资源丰富,可开发利用条件较好,应该大力发展以风能为代表的可再生清洁能源,优化我国的能源消费结构,保护生态环境。
风力发电机是风电机组的核心部件,永磁直驱风力发电机因为其结构简单、故障率低、高功率因数等优势获得了许多风电制造厂家的青睐[2]。以永磁直驱为基础运用新型的电机结构—双定子,可以有效利用电机内部空间解决单定子电机极数多、外径大、不利于大容量化的缺陷,能使电机获得更高的功率密度和转矩密度[3]。永磁电机的齿槽转矩对电机性能有着重要的影响,过大的齿槽转矩会加大电机的切入风,影响电机的能量捕获。而且永磁直驱风力发电机一般运行在低风速情况下,大的齿槽转矩还会导致输出转矩波动较大并产生噪声[4-5]。双定子电机与单定子结构相比,其齿槽转矩为内外2个电机齿槽转矩值的叠加,如设计不合理将远大于单定子结构,影响电机的平稳运行[6-7]。
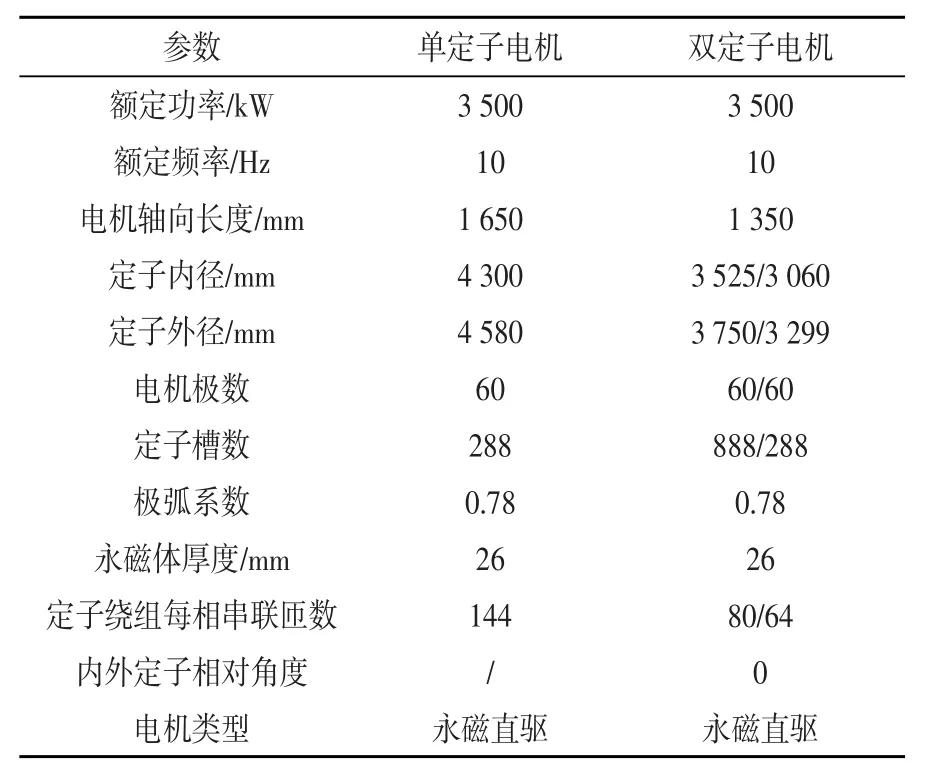
表1 单/双定子模型的初选尺寸参数
1 单/双定子电机齿槽转矩对比
分别建立一个双定子和与其同功率的单定子电机分析模型,对2个电机模型的齿槽转矩进行对比分析。双定子电机建模时应当注意其额定功率、额定电压为内外2个电机额定功率和电压值的和,内外定子绕组额定电流值相等[8-9]。2个电机的主要尺寸参数如表1所示。
建立了电机分析模型后,使用有限元分析软件计算出单/双定子电机的齿槽转矩和额定负载运行时的输出转矩,如图1、图2所示,其中A为单定子电机波形,B为双定子电机。
由图1可知,单、双定子电机的齿槽转矩幅值是15.15 kN·m和25.9 kN·m,分别占额定转矩的0.906%和1.55%。其中双定子电机齿槽转矩比单定子结构电机大71%,这不利于双定子电机的低风速启动。由图2可知,单/双定子电机额定负载时输出转矩最大波动值分别为25.5 kN·m、39.8 kN·m,说明由于齿槽转矩较大,导致双定子电机运行时的稳定性不如同功率的单定子电机,因此需要对双定子电机的齿槽转矩进行优化。
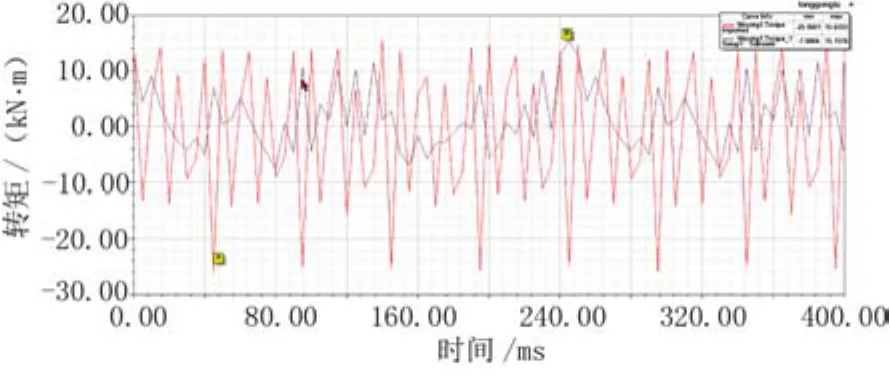
图1 单/双电机齿槽转矩波形
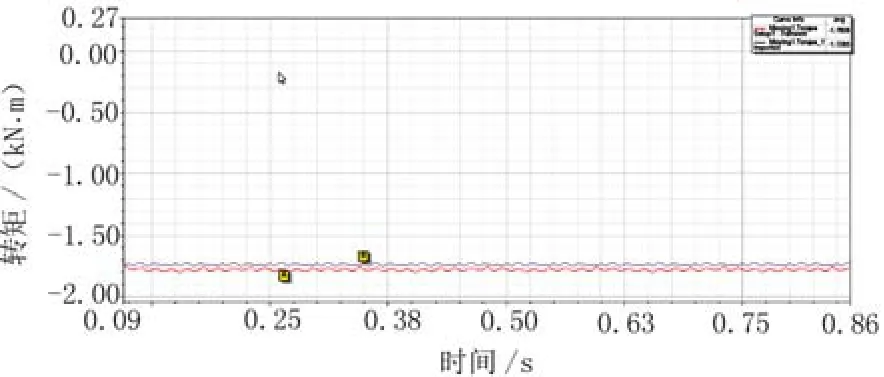
图2 单/双定子电机负载输出转矩曲线
2 双定子电机齿槽转矩原理分析
使用能量法得出双定子电机内外电机的齿槽转矩计算公式:
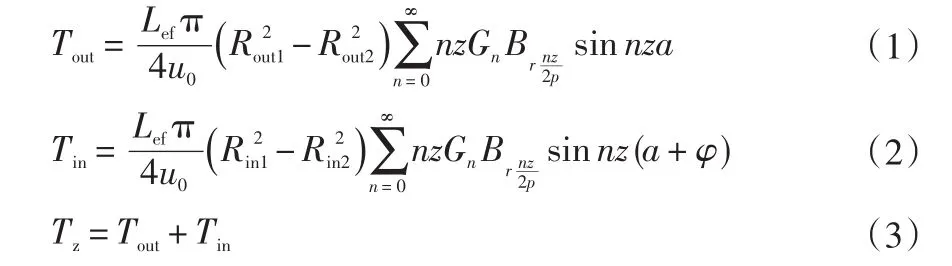
式中,Tout为外定子电机齿槽转矩;Tin为内定子电机齿槽转矩;Tz为双定子电机的齿槽转矩值;Lef为电机轴向长度内外定子电机值相等;z为电机内外定子的槽数;p为内外电机的极数;Rout1、Rout2、Rin1、Rin2分别为外定子内半径、转子外半径、转子内半径和内定子外半径;φ为电机内外定子相对位置角;n为使nz/2p为整数的最小正整数。可以假设Tout=kTin,以便对双定子电机的齿槽转矩进行计算。一般情况下,外定子电机的齿槽转矩要大于内定子电机,因此k的取值为(0,1)。根据假设将式(1)、(2)化简后代入式(3),得到双定子电机齿槽转矩的计算公式为:

3 双定子电机齿槽转矩的优化
3.1 电机的极槽配合
永磁电机的齿槽转矩是呈周期性变化的,在电机一个齿距范围内,齿槽转矩变化周期数与极数和槽数的配合有关。在公式(4)中,电机齿槽转矩周期数是使nz/2p为整数的最小正整数n,进一步得出电机齿槽转矩周期数N的计算公式为:

式中,2p为电机的极数,GCD(z,2p)表示槽数和极数的最大公约数。一般情况下,齿槽转矩的周期数越多,其幅值越小,对电机的影响也越小[5]。因此,在设计电机时要尽量使其极槽数的最大公约数取较小值或最小公倍数取较大值。为验证上述理论,以双定子电机的外电机为例取A、B、C 3个模型,其极数均取60,槽数分别为360、270、288。3个电机的齿槽转矩波形如图3所示。
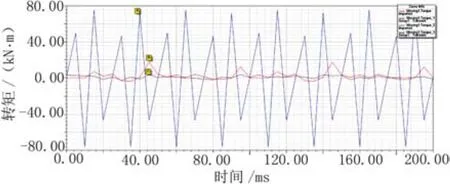
图3 不同极槽组合的电机齿槽转矩
由图3中可知,模型A、B、C的齿槽转矩最大值分别为75.5 kN·m、17.1 kN·m、9.7 kN·m,模型C的周期数为15,是3个模型中最大的,其齿槽转矩幅值最小。分析极数和槽数组合对电机空载反电动势的影响结果如表2所示。
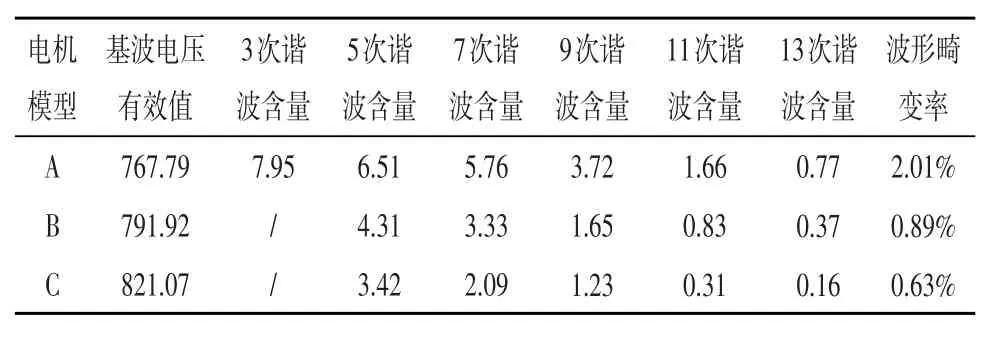
表2 不同极槽组合的电机的空载反电动势
根据图3和表2可知,电机极数和槽数最小公倍数越大时,齿槽转矩周期越多,幅值越小,电机空载线电压有效值越大,空载电压波形畸变率越小,波形正弦波越好,有利于电机的可靠运行。
3.2 极弧系数的选取
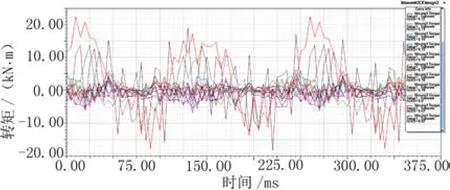
图4 不同极弧系数的电机齿槽转矩
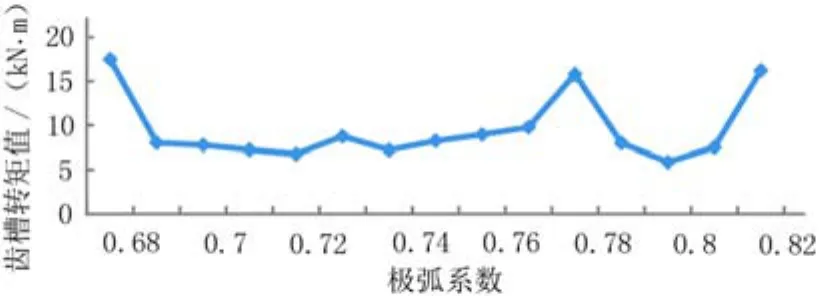
图5 不同极弧系数齿槽转矩变化曲线
3.3 内外定子相对位置角的变化
由式(4)可知,双定子电机的齿槽转矩由两部分组成。当k值确定时,后一项就为定值了,双定子电机齿槽转矩主要由前一项决定。以2 π/z为周期,随着呈余弦变化,在此周期范围内,当=1,即内外定子相对位置角φ为0或π/144时,齿槽转矩幅值最大;当=0时,φ角为π/288时,电机齿槽转矩幅值取最小值。将双定子电机内定子逆时针移动半个齿距,使内外定子相对位置角变为π/288,内外定子齿槽相对分析模型如图6所示。
使用有限元分析软件对图6的电机进行空载建模分析后,在内外定子相对位置为半个齿距时,齿槽转矩幅值为14.7 kN·m,与初始设计方案的齿齿相对φ角为0的情况相比,减小了43%左右。
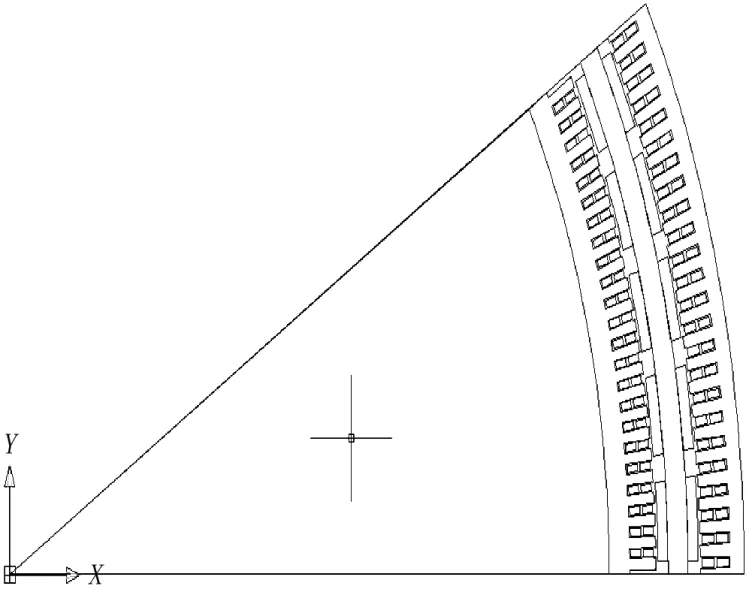
图6 双定子电机内外定子齿槽相对模型
分析内外定子相对位置改变对电机性能的影响,得出双定子额定负载状态下负载线电压和电流波形,如图6、图7所示。由图可知,内外电机负载电压和电流波形有一定的相位差,这是因为内外定子相对位置发生了改变,双定子电机负载电压、电流波形接近正弦波谐波含量较少,内外定子三相波形对称性良好。
运用傅里叶谐波分解法求出内外定子负载线电压有效值分别为668 V、506 V,同理可得到内外定子负载电流有效值为1 753 A和1 746 A,可以算出双定子电机的输出功率为3 558.46 kW。因此可以得出,在被设计中的双定子电机内外定子相对位置偏移半个齿距后,在不影响电机输出功率的情况下,电机齿槽转矩得到有效地削弱。
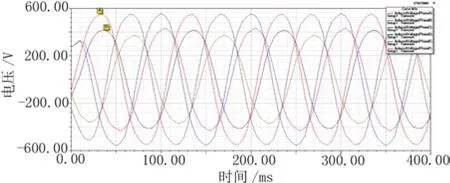
图7 负载线电压曲线
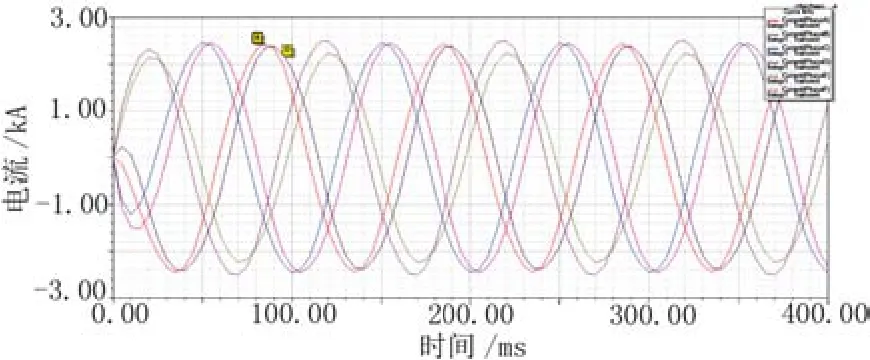
图8 负载线电流曲线
3.4 优化后结果分析
根据分析结果,在初步设计方案的基础上对双定子电机相关参数进行修正。将电机内定子逆时针旋转半个齿距,使内外定子相对位置变为齿槽正对,将转子轭部两侧表贴式永磁体的极弧系数变为0.72,电机其他相关尺寸参数和极数、槽数组合保持不变。
把修改后的双定子电机模型导入Ansys 2D中,经过空载和负载运行状态分析后,得到电机的齿槽转矩波形和负载输出转矩波形如图8、图9所示。得出双定子电机的齿槽转矩幅值为11.46 kN·m,在电机带额定负载运行时,稳定后的输出转矩波动幅值为24.7 kN·m,比初始设计方案减小了15.1 kN·m。
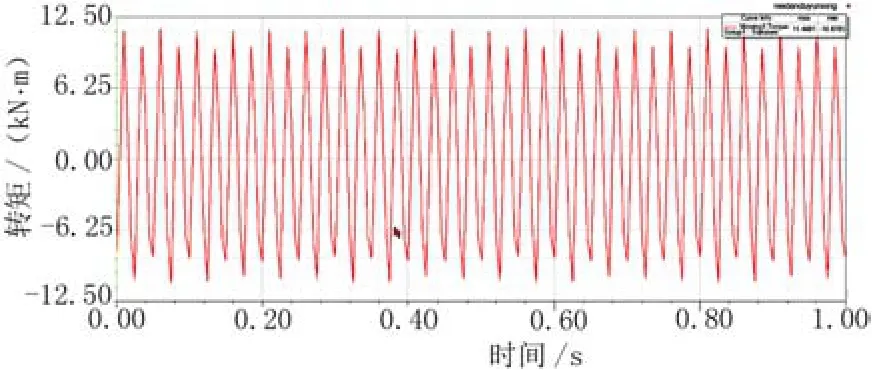
图9 优化后双定子电机齿槽转矩
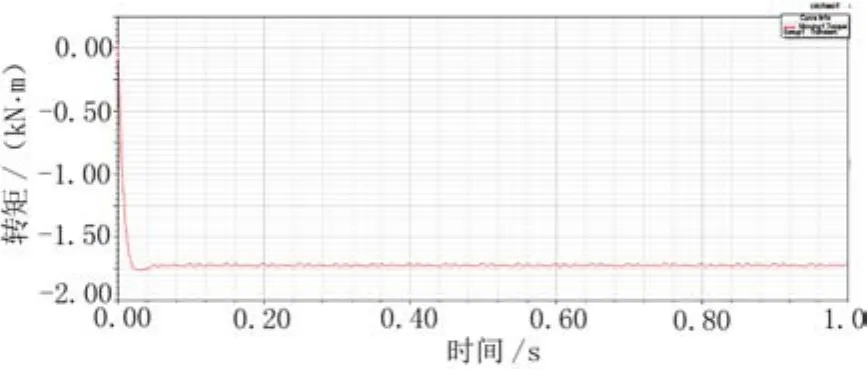
图10 优化后双定子电机负载输出转矩
4 结束语
双定子电机与单定子电机相比,结构比较复杂,如采用单定子常用的不等槽口宽度、斜极和斜槽等方法削弱齿槽转矩,会加大双定子电机的生产制造工艺难度。
本文在对双定子电机齿槽转矩计算公式进行分析的基础上,通过改变电机内外定子相对位置、电机槽数和极数的合理组合,选取合适的永磁体极弧系数对电机齿槽转矩进行削弱。通过验证,优化后的双定子电机齿槽转矩比初始方案减小了55.75%,且略小于同功率的单定子电机。同时,输出转矩波动幅值也减小了,有利于电机的平稳运行。本文所使用的方法和得出的结论对大型双定子永磁电机齿槽转矩的削弱有一定的参考作用。
