基于XFlow的热压罐成型过程温度场模拟*
2020-03-26张晨群鲍益东安鲁陵
张晨群,鲍益东,安鲁陵,宦 蕾
(南京航空航天大学机电学院,南京 210016)
热压罐工艺是当前制造大型航空用复合材料的主要工艺[1]。在热压罐成型工艺中,模具工装型面的温度场分布是影响制件质量的关键因素之一。成型过程中模具表面温度分布不均会导致制件内部存在温度梯度,以至于制件固化不同步、在结构内部产生残余应力和残余应变,最终会造成制件出现内部缺陷、发生初始破坏,严重时会影响制件的质量和使用寿命[2–4]。因此,分析和研究热压罐成型过程时模具与复合材料构件接触的表面温度分布特点对改善复合材料构件最终的成型质量具有重要意义。
当前大多数学者在模拟热压罐成型过程使用传统的以网格为基础的计算机流体力学(Computational Fluid Dynamics,CFD)软件,如CFX、Fluent 等[3,5–7],在前处理时都需花费大量时间进行网格划分等工作。而且对于热压罐成型这类流固耦合问题,传统的网格划分技术难以满足实际工程上的精度要求。因此需要寻找一种能够减少前处理时间、提升计算精度的方法来解决目前的问题。
本文将使用新一代流体力学软件XFlow,建立框架式模具在热压罐中强迫对流换热的有限元模型,并分析模具表面温度场温度分布规律及其影响因素。
XFlow 软件及其原理
1 XFlow概述
传统的CFD 软件大都采用有限体积法[8],如STAR–CCM、Phoenics、ANSYS Fluent,此外,CFX 混合使用有限体积法和有限元法。研究人员使用时需消耗大量的时间划分网格,且计算结果的可靠性高度依赖网格质量。但计算精度不是随着网格尺寸的减小而不断增加,且网格尺寸减小会增加计算资源的消耗和计算时间。XFlow 是采用格子玻尔兹曼技术的新一代CFD 软件。它的自动点阵生成和自适应优化功能避免了人工划分网格,有效缩短了前处理的时间。
2 格子玻尔兹曼方法
XFlow 所使用的LBM 方法是一种介于宏观流体连续性假设与微观分子动力学之间的介观模拟方法,同时具有微观方法的适应性广和宏观方法的不关注分子运动细节的特点,精度和计算量上均有较大优势[9]。在LBM 模型中,假设宏观流体由大量虚拟流体粒子构成,粒子仅可做两种基本运动,如图1 所示的对流和碰撞。微观颗粒不断进行“对流–碰撞”,构成了流体的宏观运动。LBM 方法的基本思想是不研究每个微观粒子的具体运动,而是利用概率密度函数研究大量粒子在格子方向上的运动概率[10–11]。
3 工作流程
XFlow 的前处理、求解器和后处理完全集成在同一用户界面环境中,其建立数值模型与分析流程如图2所示。
基于XFlow的热压罐成型过程的模拟方法
1 控制方程
由于热压罐内的热对流和热传导的换热方式,所以需要使用流体流动与热交换中的质量、动能及能量守恒方程作为模拟的基本控制方程,进行温度场的模拟。所需要求解的方程在直角坐标系下的控制方程如下所示:
质量守恒方程:
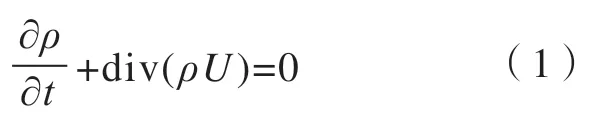
式中,ρ为流体密度;t为时间;U为流体速度。
动量守恒(牛顿运动定律)方程:
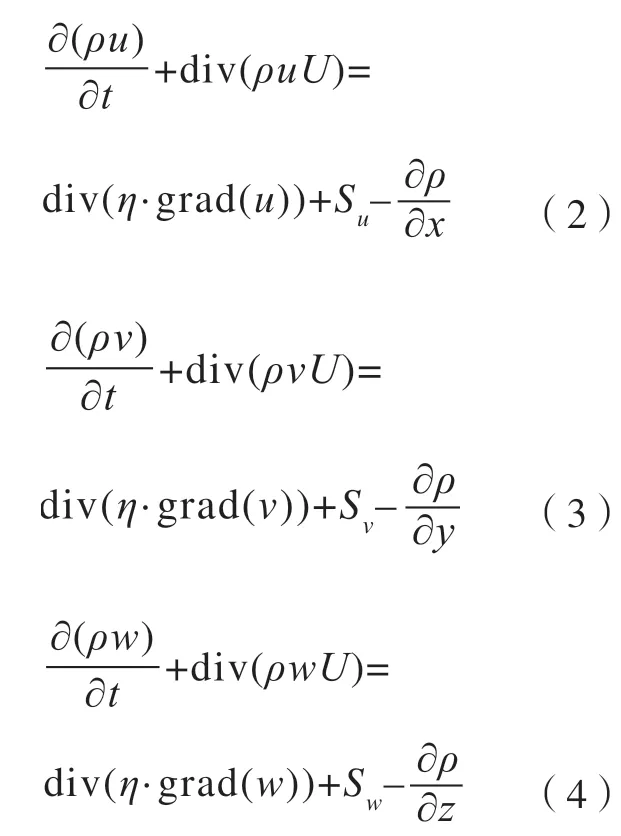
能量守恒(热力学第一定律)方程:

式中,h=h(p,T),与流体压强p和流体温度T有关;λ为流体的导热系数;Sh为流体的内热源;φ为耗散函数。
状态方程,使得方程组封闭:

对于固体区域,其能量方程为:
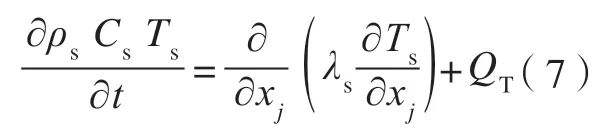
式中,ρs为固体密度;Cs为固体比热;Ts为固体温度;QT为内部热源项。
2 模型的建立与导入
热压罐中为了使温度场均匀利用风扇加快压罐内空气的流动,同时通过控制系统来控制热压罐内的温度与压强。按实际情况模拟难以实现,需对模型进行简化。对热压罐装置的简化过程如下:仅模拟工作内腔,将其简化成圆柱体模型,一端为进口,另一端为出口。模具上的一些辅助装置对温度场影响很小,对其进行简化:仅保留型板和支撑结构。利用三维建模软件CATIA建立尺寸为φ2500mm×7000mm的简化热压罐模型及尺寸为1500mm×1500mm×400mm 的简化框架式模具模型。图3 为复合材料成型模具。

图1 粒子在空间格子上的两种基本动态运动Fig.1 Two basic dynamic motions of particles on a lattice
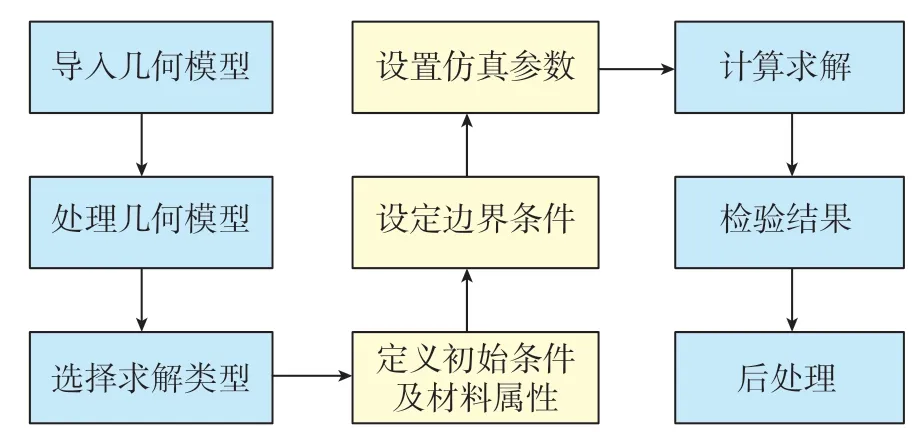
图2 XFlow求解流程Fig.2 XFlow solution flow
把建好的模具模型与热压罐模型分别导入到XFlow 并调整相对位置,如图4 所示。
3 定义求解类型
流体模型选择Single phase,因其只涉及整个流体域中的一个连续流体相,流体领域的任何一点都是相同的流体物质,符合热压罐成型过程中罐内流体的情况。
热模型选择Couple energy,该解算器可用于解释当气体高度压缩/膨胀时的压力/温度变化,适用于热压罐成型中气体温度变化且伴随加压的情况。由于热压罐内温度在200℃以下,可忽略热辐射,因此把热辐射方式设置为禁用。
接下来就是定义湍流模型。热压罐内复合材料模具的升温主要依靠热对流传热方式实现,因此还需研究分析模拟过程中与模具进行热交换的流体区域的流动状态。流体的流动状态一般分为层流与湍流,使用雷诺系数Re 的大小来判断。
当空气在热压罐内流动时,相当于气体在管内流动,则其雷诺数为

式中,ρ为气体密度,u为流体流动速率,μ为气体的动力黏度,D为热压罐直径。
热压罐内流体为空气,密度为1.225kg·m–3,动力黏性系数取值1.82×10–5Pa⋅s。风速1.5m/s,热压罐直径为2.5m。
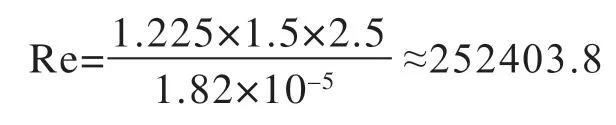
通常雷诺数与流动状态的对应关系如下:
(1)Re ≤2300,为层流;
(2)2300 ≤Re ≤8000,为层流与湍流的过渡区;
(3)Re ≥8000,为湍流。
根据计算出的雷诺数可知罐内气体流动类型为湍流,选择自动适应壁面的局部涡流模型。
4 定义初始条件与材料属性
重力对温度场影响极小,为减少计算量把重力加速度设为0。初始温度设为288K(室温),初始压强设为标准大气压。接下来定义材料属性:罐内流体为空气,按空气的属性定义流体参数。热压罐成型过程包含复杂的流固耦合问题,定义模具为共轭传热属性,让模具热传导与流体对流同时进行;模具的型面和支撑结构均采用Q235。空气与模具的热属性如表1 所示。
5 定义边界条件与仿真参数
(1)入口设置。
圆柱模型一个端面作为进口,边界条件设置为Inlet–Velocity,设定入口速度为风速,热边界条件为气体温度–时间变化函数。
(2)出口及壁面设置。
设置出口类型为Convective outlet,即出口处的静压和速度都是从内部域推断出来的。同时设置热压罐圆筒壁面为Wall,热边界条件类型为绝热类型。
(3)仿真参数设置。
设置仿真时间,XFlow 无需划分网格,只需定义求解尺寸即粒子大小。
模型精度验证及模具型面温度场分析
1 热压罐成型模具传热分析模型精度验证
为了验证XFlow 应用在热压罐温度场模拟上的可行性,需要分析仿真结果的精度。将仿真得到的模具表面的温度数据和实验室中利用热电偶检测得到的数据[5]进行对比,温度监测点如图5 所示。以0.025K/s的升温速率升温至第4800s,此时模具表面温度分布如图6 所示。
模具是对称结构,选择沿对角线上的数据。选取X01、X09、X13、X17、X25 这5 个坐标点的数据进行对比,见表2[5]和表3。
计算得到的平均相对误差为1.83%,最大相对误差为4.44%。误差来源主要有:简化了热压罐模型和其他装置;文献[5]中的模具为较为平缓的曲面,但本文所用模具模型将其近化为平面;XFlow 设置的传感器是试验监测模拟点的近似取值。总之,仿真得到的数据与试验数据很接近,平均误差较小,可以使用XFlow 软件分析热压罐成型的模具温度场。
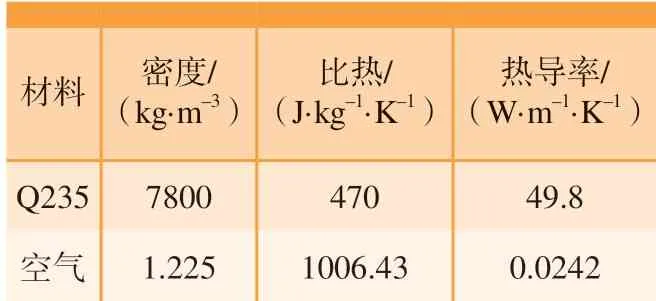
表1 材料的热属性Table 1 Thermal properties of materials
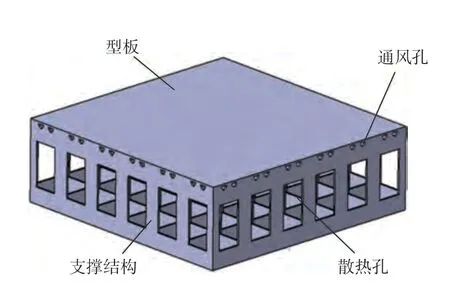
图3 框架式模具简化结构Fig.3 Simplified structure of frame die

图4 框架式模具和热压罐模型Fig.4 Frame type mold and simplified autoclave model

图5 试验监测点分布图Fig5 Distribution map of experimental monitoring points

图6 模具表面的温度分布Fig.6 Temperature distribution of type plane mold
2 模具型面温度场分析
在如图7 所示的简化工艺曲线下,设定风速为1.5m/s,初始加压加6个大气压,对热压罐成型过程模拟。
研究模具温度场的最终目的是改善复合材料构件在固化过程中的外部温度场分布,模具上表面与复合材料构件接触,因此本节主要讨论模具上表面的温度场分布情况。升温、保温及降温各阶段结束时,模具上表面的温度分布情况如图8 所示。
在进行实际试验时,不方便测量模具上大量点的温度值,一般通过放置热电偶监测个别点在试验过程中的温度。因此大多数学者使用最大温差值表征模具的温均性。但最大温差值仅利用了温度最大值和最小值两个数据,不能反映模具整个上表面的温均性。在有限元模拟时可以采集大量点在成型过程中的温度变化,因此本文引入了标准差这一统计量,标准差将更多的数据引入计算,更加能反映一组数据的均匀性,温度方程能更好地体现出模具上表面的温均性。标准差是在几何表面A上积分标量与平均值的偏差,计算公式为:

表2 监测点热电偶试验数据Table 2 Monitoring thermocouple test data
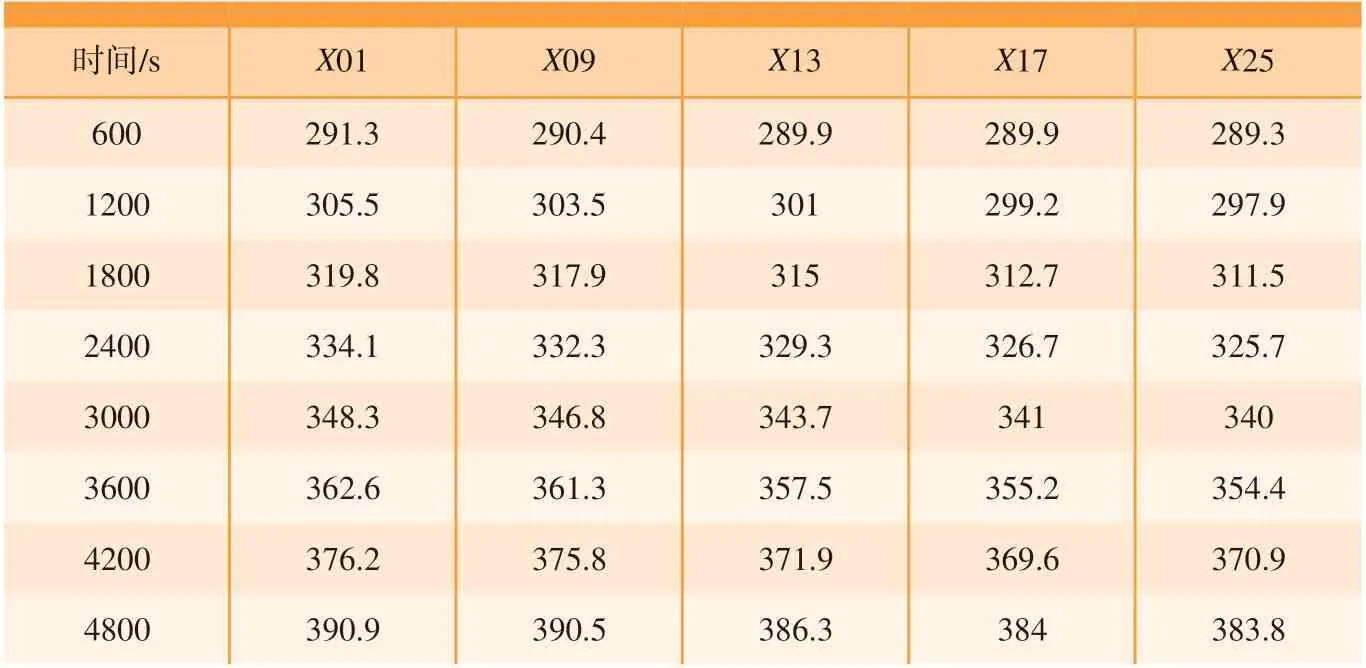
表3 监测点XFlow模拟数据Table 3 Monitoring XFlow simulation data
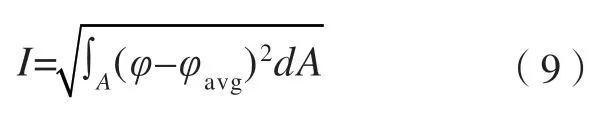
通过XFlow 后处理中的表面积分功能可以计算模具上表面温度标准差分布,将结果整理得到图9。
结果表明:升温阶段,模具迎风端的温度高,最高点在迎风端的边角处,温度最低处集中在背风端,温度呈阶梯状分布,温差逐渐增大;保温阶段,温度分布比较均匀,温差随时间持续减小;降温阶段,趋势与升温过程相反,背风端温度最高,迎风端温度最低,温度呈阶梯状分布,温差不断增大。升温时温度分布呈阶梯状的原因主要是:模具型面的热量主要来自于流经上表面流体的对流换热和底部支撑框格的热传导[10]。气体流过模具表面可看作是气体外掠平板,紧贴模具的气体会形成热边界层,流体的黏性损耗了动能,因此边界层中速度沿风向降低,且边界层厚度变厚,如图10 所示边界层越厚,热阻越大,传热效率越低。底部支撑框格的热量由流体的射流冲击换热产生,迎风端框格阻碍气体流向背风端,迎风端框格温度高于背风端与模具的传热更多。此外可以看出,模具上表面的前端和侧面的温度均高于内侧的温度,原因是模具周边和高温气流之间的对流传热更强。
工艺因素对模具型面温度场的影响规律
热压罐工艺中可能对模具温度场产生影响的工艺因素有:罐内风速、升温速率及降温速率等[12]。由图9 可知,保温阶段罐内温差逐渐减小,温差出现在升、降温阶段,因此在研究升降温速率对模具表面的温度影响规律时,本文仅对升温阶段和降温阶段进行模拟。
1 风速
在XFlow 中将风速分别设置为:0.5m/s、1.5m/s、3m/s 和5m/s,入口温度按图7 设置。整理不同风速下模具型面温度标准差,如图11、图12所示。
结果表明:在升温阶段,模具型面的最大温度标准差出现在升温结束时;在升温后期,风速越大,模具型面的温差最大值越小,温差的增加越缓慢。在保温阶段,风速越大,模具型面温度趋于均匀所需的时间越短。在降温阶段,模具型面的最大温度标准差出现降温过程中,温差在降温后期停止增加,风速越大,温差最大值越小,出现时间越早。综上,提高风速可以有效减小模具型面温差。

图7 简化工艺曲线Fig.7 Simplified cured temperature curve
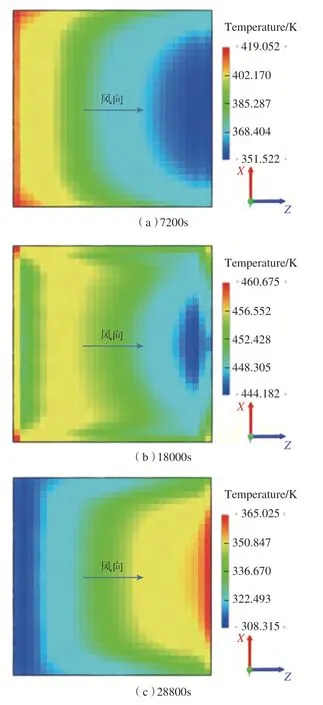
图8 模具上表面的温度分布Fig.8 Temperature distribution of type plane mold

图9 模具上表面温度标准差分布Fig.9 Temperature standard deviation distribution of type plane mold
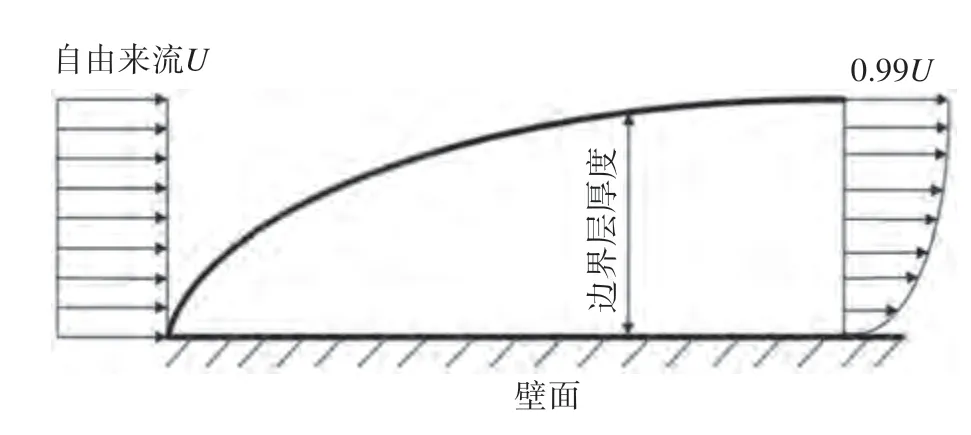
图10 边界层示意图Fig.10 Boundary layer of plane
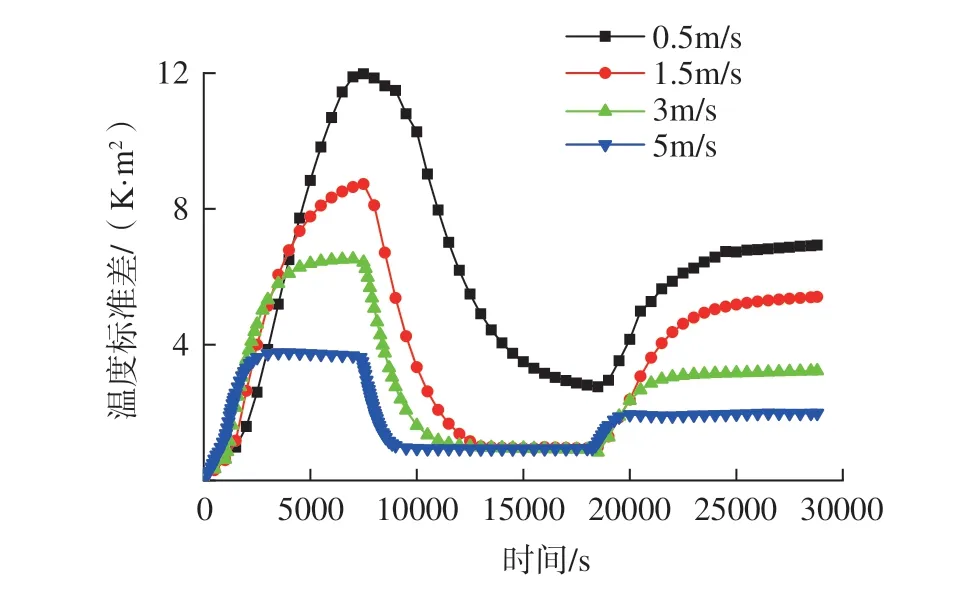
图11 不同风速下的温度标准差对比Fig.11 Comparison of temperature standard deviation under different wind speeds

图12 不同风速下的最大温度标准差Fig.12 Maximum standard deviation of temperature at different wind speeds
2 升温速率
将升温速率分别设为:1K/min、1.5K/min、2K/min 和3K/min,模具的初始温度设为288K,经不同升温速率的升温过程,温度升高至468K 结束,风速设为1.5m/s。整理不同升温速率下模具型面温度标准差,如图13、图14 所示。
结果表明:模具型面最大温度标准差随着升温速率的增大而明显增大,最大温度标准差的值随升温速率的增长基本呈线性增长。
3 降温速率
将降温速率分别设为:0.5K/min、1K/min、1.5K/min 和2K/min,模具的初始温度设为468K,经不同降温速率的降温过程,温度降低至288K 结束。整理不同降温速率下模具型面温度标准差,如图15 和16所示。
结果表明:模具型面最大温度标准差随着降温速率的增大而明显增大,最大温度标准差的值随升温速率的增长基本呈线性增长。
结论
(1)基于XFlow 软件建立了热压罐成型模具温度场仿真的数值模型,将模拟数据与试验结果对比,平均误差为1.83%,最大相对误差为4.44%。
(2)分析了热压罐成型过程中模具表面温度分布情况,引入了温度标准差作为模具表面温度均匀性的表征值,结果表明:温度标准差在升、降温阶段不断增大,保温阶段不断减小。
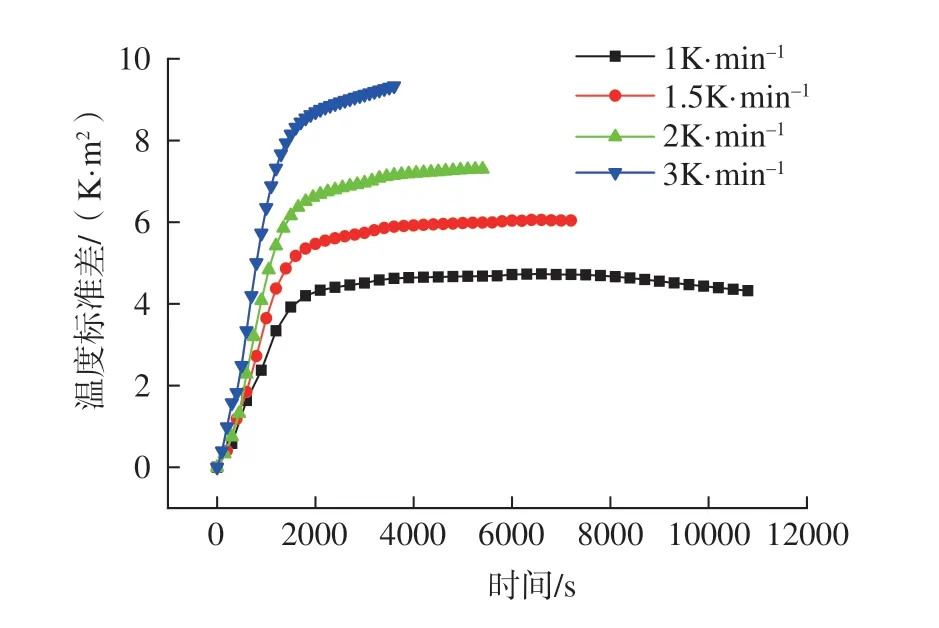
图13 不同升温速率下的温度标准差对比Fig.13 Comparison of temperature standard deviation at different heating rates
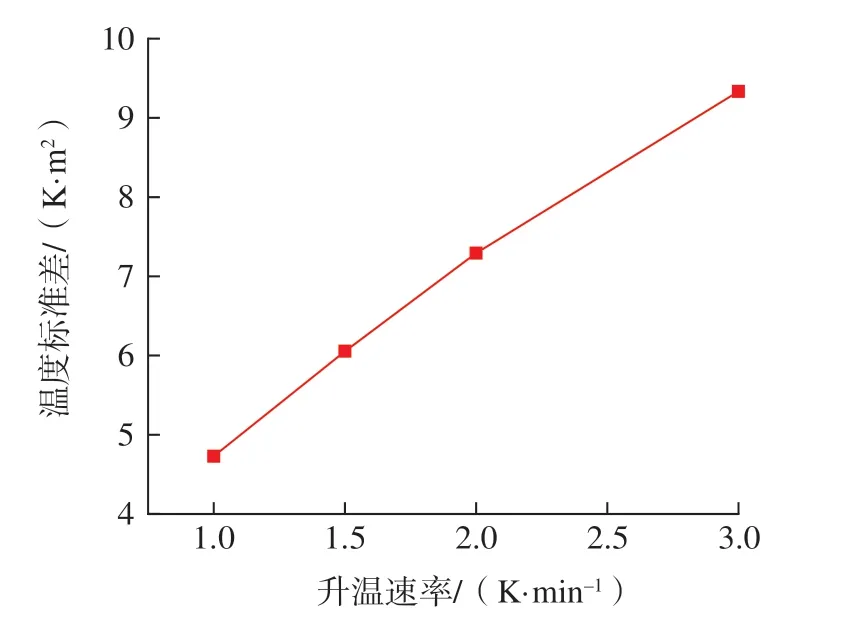
图14 不同升温速率下的最大温度标准差Fig.14 Maximum standard deviation of temperature at different heating rates
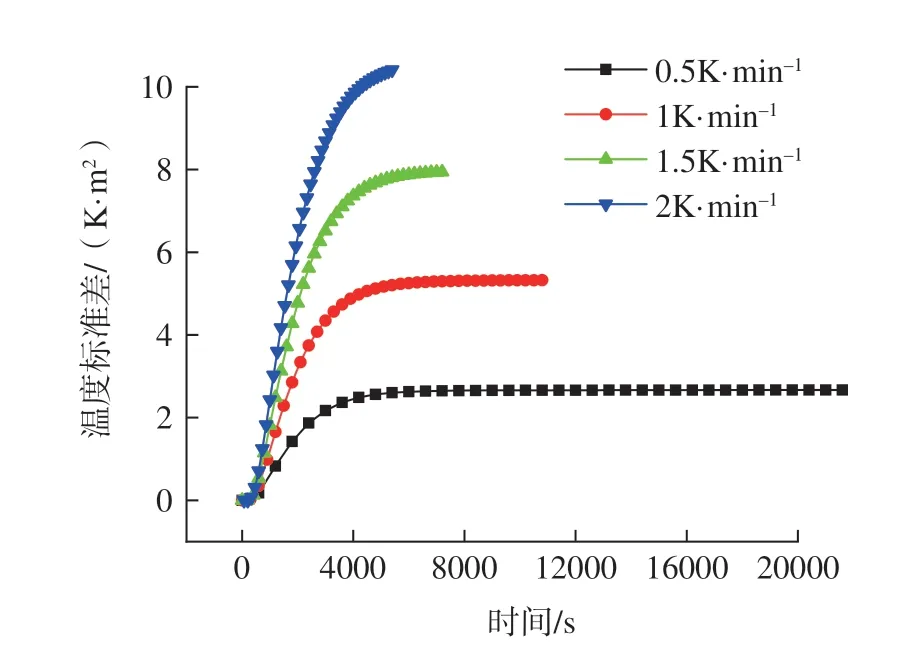
图15 不同降温速率下的温度标准差对比Fig.15 Comparison of temperature standard deviation at different cooling rates

图16 不同降温速率下的最大温度标准差Fig.16 Maximum standard deviation of temperature at different cooling rates
(3)研究了风速、升温速率和降温速率对模具型面温度场均匀性的影响。结果表明:增大风速、减小升降温速率均可以有效降低模具型面温度标准差。
(4)采用基于LBM方法的XFlow 流体力学软件分析框架式模具在热压罐中模具表面温度场分布,可以大幅减少前处理时间,并能够提高计算精度。
