企业债务与经济增长：基于增长理论的量化分析*

李连发， 戚逸康

一、引 言

非金融企业债务和资本积累之间的关系是当前我国经济工作中的重要关系。2014年开始，企业债务已经日益受到社会的关注(王宇和杨娉，2016)；2014年中央经济工作会议提出，要化解高杠杆为特征的风险。2015年之后，中国经济逐渐步入中高速增长的“新常态”。2015年中央经济工作会议将“去杠杆”作为经济社会发展的五大任务之一。这一政策延续到2019年，2019年《政府工作报告》将稳定宏观杠杆率作为政府工作目标之一。从国际清算银行公布的数据看，我国非金融部门信贷/GDP比例在2008年之后一直攀升，2017年开始基本稳定在253%的水平，居于高位(图1)。根据图1，我国非金融部门企业债务与GDP比例在2008年有较大增长，并在随后保持了持续增长态势，2017年这一比例的增长势头有所缓和。

2019年，我国由于国际形势变化和国内经济发展走入新阶段等原因，经济下行的压力逐步显现。结合这一背景，本文选择非金融企业去杠杆和经济增长关系为研究对象。

与本文联系最密切的债务文献是Hellwig & Lorenzoni(2009),该研究定义了由债务不违约推导出的最大的债务上限(用原文的话就是不太紧的债务上限)；本文的边际贡献在于将这一债务上限与资本积累联系起来。传统的增长模型讨论储蓄率、创新、人力资本等非金融因素，这一分析传统假设金融市场是完备的。只有在金融市场不完备情况下，非金融企业债务才有可能影响资源配置和经济增长。Milbourne(1997)在新古典模型的框架下加入外债和政府债务因素，但是模型没有提及金融市场完备的概念。同样，在讨论最优债务比率时，闫先东和廖为鼎(2017)与马勇和陈雨露(2017)也没有涉及金融市场不完备的具体形式。

图1 我国非金融部门信贷/GDP比例(2010—2018) 数据来源：国际清算银行

有研究不考察非金融企业债务，而是从财政政策角度考察政府债务，比如，Panizza & Presbitero(2014)的实证分析发现，控制货币贬值效应，政府债务和经济增长不再显著相关。Reinhart & Rogoff(2010)曾提出著名的“90%、60%”标准，即当一国的政府债务超过GDP的90%或外债超过GDP的60%时，债务会拖累经济增长。

刘伟和李连发(2018)将最优杠杆率与资源配置联系起来：最优杠杆率、偿还债务和企业债务期限之间存在联系；企业具备融资条件不意味着融资带来资源配置效率；反之，企业不具备融资条件，也不意味着融资就不能带来资源配置效率。

企业异质性与企业债务的结合给这一研究领域带来了新结论。蒋灵多和陆毅(2018)与纪洋等(2018)围绕“结构化去杠杆”，即将国有企业和非国有企业区别开来，他们的政策导向是要消除国有企业的预算软约束。汪勇等(2018)和周俊仰等(2018)认为在去杠杆操作中，对不同企业或不同经济主体，应该做到兼顾而不能一刀切，着力实现转杠杆而不是纯粹的去杠杆。刘晓光和刘元春(2018)以及王宇伟等(2018)通过分解债务率(债务/GDP)指标，将对宏观杠杆率的分析深入到企业微观层面，指出资源错配以及企业资产使用效率的不足是在“去杠杆”过程中值得关注的问题。刘贯春等(2017)认为，在“去杠杆”过程中应该注意企业金融资产配置。

与以上文献不同，本文将动态关系归纳为(包含非金融企业债务)增长模型中的差分方程。在资本积累过程中，由于购买物质资本需要举债，因此债务的规模影响了资本积累的规模。本文通过将理论模型参数化，将参数与我国实际情况进行比对，进行量化模拟分析，以考察去杠杆操作的经济后果。本文接下来的安排如下:第二部分主要阐述本文的理论分析框架;第三部分是对模型的拓展;第四部分在理论上讨论债务偿还安排;第五部分是数值模拟;最后一部分是总结。

二、债务对资本积累和经济增长动态影响的理论刻画

(一)模型

索洛模型(Solow, 1956；Swan, 1956)给出了资本积累和经济增长的动态关系，但是，假设购买物质资本所需要的债务不会受到上限的限制。本文假设购买资本的债务上限是紧的，但同时，又在达到不违约上限意义上不是太紧(Hellwig & Lorenzoni, 2009)。虽然达到了债务不违约的债务上限，但依然满足债务不违约的限制条件，所以在均衡状态下债务不违约。由于生产资本中的一部分来自债务，降债务的过程与稳态是联系的。在没有债务上限情况下，索洛模型中的稳态要求新增资本与折旧、人口增长和技术进步等因素一致，而且生产函数的凹性确保了稳态的存在性、唯一性和稳定性。在明确考虑债务上限后，经济稳态的存在性、多重性、稳定性受债务上限的影响。

生产函数F(Kt,AtLt)满足规模报酬不变、二阶连续可微；紧凑形式f(kt)满足稻田条件，一阶导数大于零、二阶导数小于零。投入要素为资本(Kt)和劳动(Lt)两种，技术(At)是劳动增进型的，劳动和技术分别以n和g的增长率增长，即满足Lt+1=(1+n)Lt和At+1=(1+g)At。每单位有效劳动的资本存量k满足k=K/AL，其变化量Δk的离散化表达式为

(1)

资本积累的差分方程为

Kt+1=Kt-δKt+sF(Kt,AtLt)-Dt+Dt+1

(2)

式(2)中，Dt和Dt+1分别是t期应偿还的真实债务(上期的债务上限)和t期新增的下期偿还的真实债务(当期的债务上限)，在这里我们假定债务的期限只有一期，即t期的新增债务Dt+1在t+1期需要偿还。生产函数的s部分可以增加下期的资本，δ是折旧率。

式(2)债务增加资本，不能改变技术进步参数。假设只有一种商品，它既是产出品，又可用作资本、偿还债务。根据式(2)，改变下期资本的是净债务；只有在当期净偿债额不为零时，下期资本才受债务的影响。

将式(2)带入到式(1)中可得

(3)

[1-δ-(1+g)(1+n)]k+sf(k)=d-(1+g)(1+n)d

(4)

式(4)移项后得

sf(k)=-(g+n+ng)d+(n+g+δ+ng)k

(5)

式(5)体现了债务对经济稳态的影响。

(二)稳态时债务影响的具体分析

1.d=0

这种情况退化为没有债务上限的资本积累稳态条件。资本积累没有受到债务的约束，债务上限没有对稳态资本水平产生影响。此时，存在一个使实际投资(sf(kt))和持平投资((n+g+δ+ng)kt)相等的点E，如图2。在该点左侧，实际投资大于持平投资，故k上升；在该点右侧，实际投资小于持平投资，故k下降。

图2 债务上限不影响稳态资本的情况

k不论大于或者小于k*，都会最终收敛于E点；在该点，产出增长率为n+g+ng，资本增长率同样为n+g+ng，而人均产出增长率为g。

2.d<0

随着人口和产出增长，为保持资本稳态，需要偿还固定的债务d。以下分三种情况讨论，分别如图3、图4、图5所示。

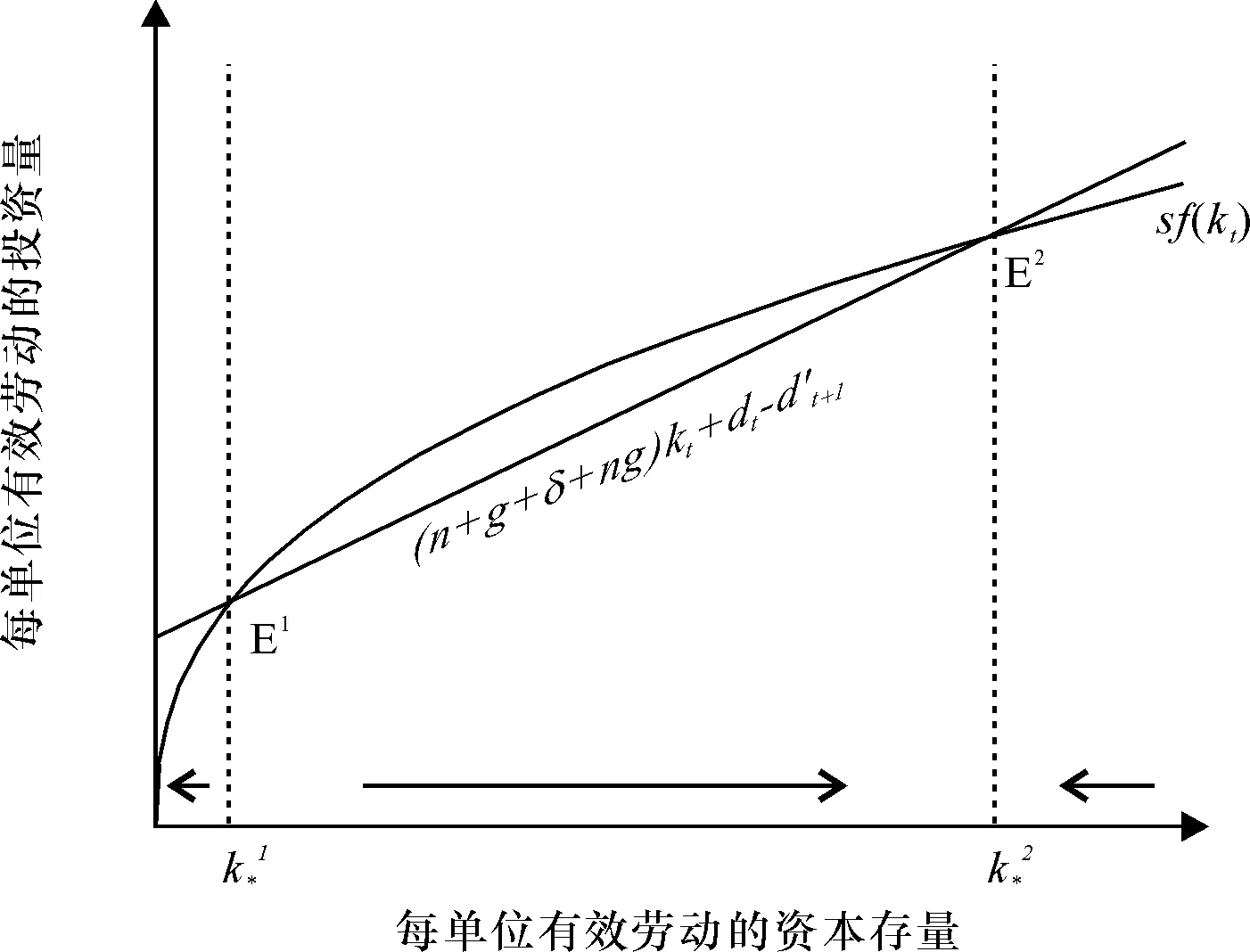
图3 进入偿债阶段出现两个稳态的情况

图4 进入偿债阶段出现一个稳态的情况

图5 进入偿债阶段却没有稳态资本的情况

3.d>0

如果稳态时不仅没有净的还债压力，而且还有进一步为资本积累提供债务支持的空间(如图6)。这种情况下，唯一稳态点E(图6)对应的资本积累水平会高于d=0时的水平，债务不仅带来了更多稳态资本，而且稳态点是稳定的。

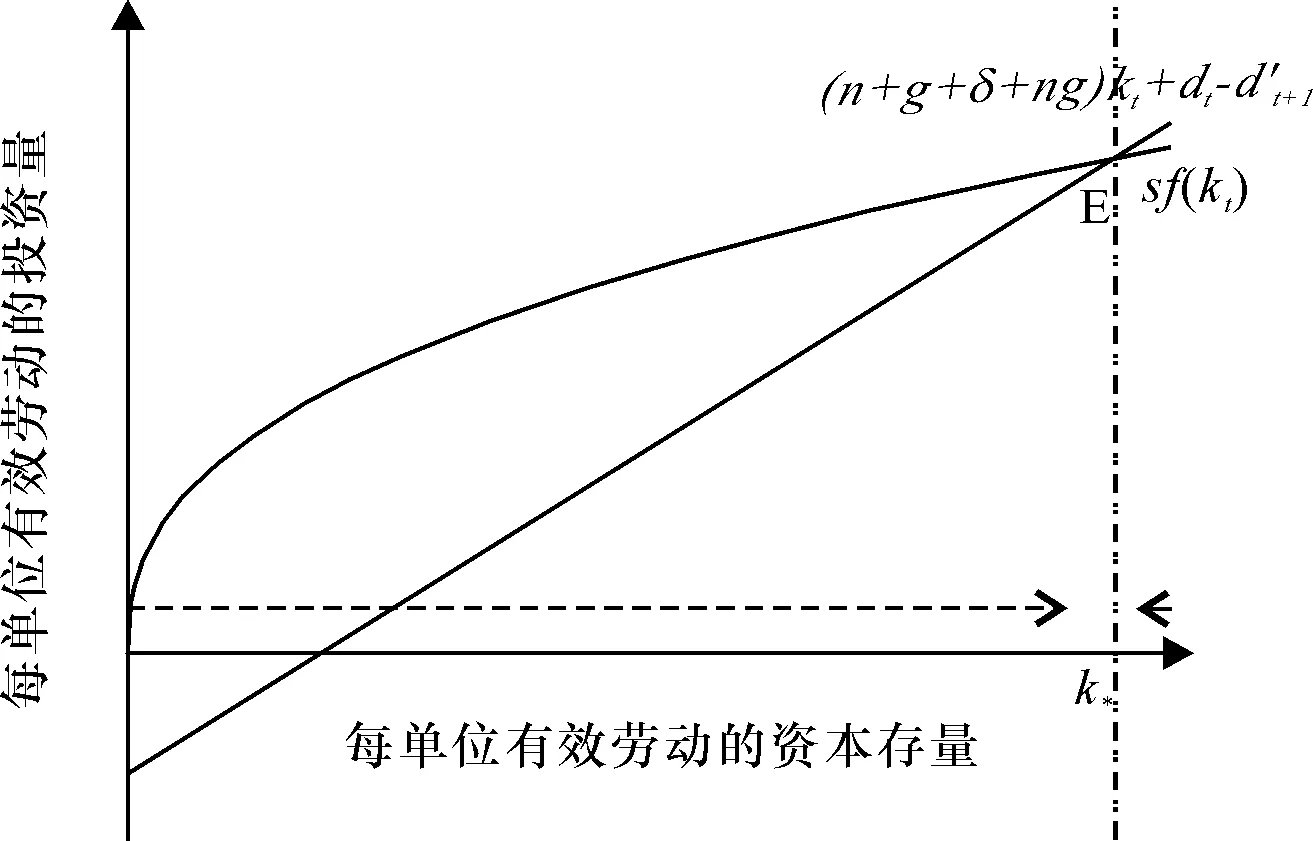
图6 可以持续为资本积累提供债务支持存在一个稳态的情况

图7 不同d下稳态点的比较静态分析

图7将d等于、大于、小于零三种情况集中在了一起。点E0是企业无偿债压力下的稳态，点E1和E2是企业有偿债压力下的稳态，点E3是企业有进一步借款空间时的稳态。在去杠杆过程中，随着偿债压力增大，平衡增长路径(E2较之E0)下的稳态资本存量会减小，部分资本存量小的企业会退出经营(E1)。反之，当企业可以继续借款时，资本存量稳态值会提高(E3较之E0)。

三、模型的拓展：消费者效用最大化和资本积累外部性

消费者效用最大化对应的是资本积累的动态效率，也就是说，从消费者终身效用最大化的角度来确定最佳的资本存量。在考虑最佳资本存量时，一般不考虑资本积累的正向外部性。是否考虑资本积累的正向外部性，带来的结论非常不同。在图8中，(sgold+α)f(k) 曲线对应的是考虑正向外部性(α)的消费者效用最大化的情况，sgoldf(k)曲线对应的是没有考虑正向外部性的消费者效用最大化的情况。

图8中，在债务上限无穷大情况下，kgold点是没有考虑正向外部性的“黄金律”资本存量水平，该资本水平所对应的平衡路径是B点；考虑资本积累正向外部性，同样在债务上限无穷大情况下，稳定点为E0，资本存量从kgold增加到对应的资本水平。

图8中E1和E2两个稳态点的出现，只有在考虑资本积累正外部性情况下才有可能。

在不考虑资本积累外部性的情况下，假设债务上限为无穷大，消费者效用水平最高所对应的资本的边际产出满足以下特定条件，即

f′(kgold)=n+g+δ+ng

(6)

图8 考虑资本积累正向外部性和消费者效用最大化的稳态情况

四、净偿债规模

sf′(kbound)=n+g+δ+ng

(7)

将式(7)带入式(5)中并经简单变换后可得

(8)

d=-sf[f′-1(MPK)]+[(1+g)(1+n)+δ-1]f′-1(MPK)

(9)

其中MPK是资本边际生产率。式(9)表明可通过不同的债务偿还额度，引导企业趋向于不同的资本边际生产率水平。

图9 资本积累外部性消失前净债务规模临界值和外部性消失后(长期)稳态资本

五、债务偿还安排

(10)

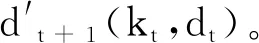
图10 一种结构化的债务偿还安排

六、参数校准和数值模拟

(一)基准模型

(11)

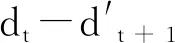
考察劳动要素增长率n，根据Romer(2012)的做法，采用国内人口自然增长率替代难以直接估算的n。国家统计局公布的数据显示，2017年我国人口的自然增长率为5.32‰，此为n的近似取值。对于g，文献中许多学者曾估算过我国的全要素生产率增长率，例如蔡跃洲和付一夫(2017)的估算结果指出2010至2014年间，中国的TFP增长率约为2.2%；而陆旸和蔡昉(2014)的估算指出2001至2010年间，TFP增长率约为3.72%；更近一些的估算结果，盛来运等(2018)指出2017年我国的TFP增长率约为3.14%。结合上述不同估算结果，本文将g的值选定为3%，一方面这一值处在不同估算结果所隐含圈定的范围之内，另一方面比较贴近时间最近的估算结果。

对于折旧率δ的处理，文献中多采用两种思路，一是一种“拇指规则”，意为直接采用一个假定的折旧率，例如王小鲁等(2000)以及郭庆旺和贾俊雪(2004)均采用了5%的折旧率；二是通过设定资本的相对效率进行估算，张军等(2004)和单豪杰(2008)基于这种思路，其结果均指出折旧率约在10%左右，与前述差异较大。近期文献对我国折旧率的估算同样存在结果差异大的问题，如陈昌兵(2014)的结果是约5.6%而王维等(2017)的估计给出了超过14%的平均折旧率。面对这种局面，本文依旧采取折中策略，即取10%的折旧率作为δ的近似。资本积累正向外部性参数s为55%。

表1 参数校准

图11 不同债务偿还比例对稳态的影响

(二)敏感性分析

考虑到当前文献对折旧率和全要素增长率的估计差异较大，本文需要对参数的校准取值进行敏感性分析，以增强结论的稳健性。敏感性分析中各参数的取值区间如表1所示，其中，折旧率的取值范围较宽，劳动要素增长率的取值范围较窄，这与文献中相应取值的差异正相关。敏感性分析的结果显示，劳动要素增长率对本文的结果影响很小。对于全要素增长率，在其2%～5%的取值范围内，当债务无上限时，经济的唯一稳态点对应的资本积累水平范围约为人均12.5～19.2万元，始终低于当前的资本积累水平，临界债务偿还比例范围为5.6%～6.9%。全要素增长率(TFP)的取值越高，稳态资本积累水平就越低，临界偿债比例也越低，这说明TFP越高，我国当前资本积累过度的程度就越高，就更需要去杠杆、降债务，不过此时去杠杆的力度不宜大，因为偿债临界值低，降债务代价大。对应于资本积累正外部性参数50%～60%的取值范围，稳态人均资本分布于13.6～18.4万元的范围内，依然低于当前的资本积累水平，临界偿债比例分布于5.3%～7.6%的范围内。资本积累正外部性参数的取值与稳态人均资本和临界偿债比例均正相关。

折旧率的取值范围比较大，折旧率取值为5%和15%时的稳态如图12所示。显然折旧率越高稳态人均资本越低，临界偿债比例也越低。当折旧率为5%时，债务无上限条件下，稳态人均资本水平要高于《中国国家资产负债表2018》给出的实际水平，此时我国经济的资本积累并不过度。不过，当折旧率为5%时，稳态人均资本仅为8.8万元，远低于我国实际水平。当折旧率取值高时，去杠杆的操作空间变小，折旧速度更快的条件下，去杠杆会进一步压缩资本积累空间，此时经济代价大。总体来看，折旧率的变动对于临界偿债比例的影响最大，此时该比例分布于4.7%～10.1%之间(如图12)。

七、结 论

非金融企业债务如果没有上限限制，资本积累不会受到债务规模(假设债务规模达到债务上限)的影响，这对应传统的没有考虑债务的假设金融市场完备的增长模型。本文考虑资本积累受到债务规模上限的影响，这种影响对稳态的多重性、存在性和稳定性均带来了新的结论。偿债净额小于临界值时，资本存量不大，可能会落入“资本积累不足陷阱”。短期内，资本积累可能存在正向外部性，而长期内资本积累的外部性会消失；长期内消费者效用最大化所对应的稳态资本水平代表了长期的资源配置效率，这一资本水平对于确定长期最优的债务规模提供了参考。

图12 折旧率分别取5%和15%时的稳态

在对模型进行参数化的基础上，结合实际数据，对参数进行校准后，得到了比较静态的结论。去杠杆操作的经济代价主要是短期内经济增长率下降，以及严苛的信贷环境会使资本积累不足的企业退出经营。但是，去杠杆有利于资本积累水平的优化，所以坚持去杠杆在长期内有助于经济增长。鉴于此，如果要协调去杠杆和增长，减小去杠杆带来的经济成本，那么结构化去杠杆的思路值得借鉴。结构化去杠杆有可能在整体去杠杆力度不变的基础上，同时实现资本积累水平的优化和杠杆率的下降。数值模拟结果显示，绝大多数参数取值下，我国真实资本积累水平高于债务无上限条件下的稳态水平，因此有必要去杠杆。合理的去杠杆力度虽然在不同的参数取值下不同，但总体来说，每一期不能超过总债务量的10%。根据本文的基准模型，每一期债务偿还额的上限为非金融企业债务总额的6.4%。不过，折旧率和全要素增长率对去杠杆操作的可行范围存在影响。