一种面向实时风险预测的工业报警优先级评估方法*

王 佳，陈 勋

（1.中国软件评测中心，北京 100048；2.中国电子科技网络信息安全有限公司，四川 成都 610000）

0 引 言

报警优先级评估是报警管理系统的一项重要内容，主要用来表达不同过程变量超越报警阈值的危害性，能够帮助工厂操作人员有针对性地处理实时产生的报警，采取更加有效的措施[1-6]。报警变量优先级的确定应该同时考虑对工厂和系统的实时危害程度和响应的紧急程度[7]。

风险危害程度一般有定性和定量两种分析方法[8]。定性的分析方法有危害和可操作分析（Hazards and operability Analysis）、过程危害分析（Process Hazards Analysis）、传统的失效模式与影响分析（Failure Mode and Effects Analysis）以及复合有向图等[9-10]；定量方法包括建立故障树分析模型[11]、马尔可夫模型以及因果关系分析图等。此外，随着安全分析理论的进一步发展，涌现出贝叶斯（Bayesia）网络、复杂网络模糊映射等与多学科相结合的分析方法。上述方法能够对变量的风险进行描述和建模，但是主要依靠专家经验，并且由于变量不确定性，不能从实时状态变化的角度给出变量的风险转移过程。Chang[12]等通过建立危险发生概率、潜在危险影响和过程安全时间的综合模型，对整个过程的安全报警进行优先级评估来减少报警的数量，但是需要依靠专家经验，不能有效运行过程中检测的数据，“实时性”明显不足。Foong[13]等结合整个过程中的数据和专家知识，利用模糊推理对产生的报警变量进行优先级排序，但是欠缺对报警发生时间的考虑。由于随机不确定性因素的影响，各个时刻之间的状态转移可用Markov过程描述，但是转移概率不能直接测量获取具有时变的特征，每一时刻的转移概率值不是固定的。目前，粒子滤波对非齐次转移概率的估计不受过程噪声和测量噪声限制。相比Kalman滤波，主要利用一系列离散采样值近似实现转移概率的最大后验估计，得到状态的估计值[14-15]。

因此，考虑到变量的不确定性因素，本文针对报警风险状态转移过程中的状态和时间两个方面进行分析，建立幅值裕度和时间裕度定量性分析指标。由于受到外界的干扰转移概率的随机时变性，建立动态Markov状态转移模型描述报警状态转移和时间变化过程，通过粒子滤波估计状态转移矩阵，得到系统状态变化的估计值，由此提出了一个新的报警优先级评价的系统优化方法。

1 报警风险评价指标

1.1 幅值裕度指标

一般情况下，工业过程报警状态是从低报警到高报警状态进行演化的，因此在对报警危害的严重程度进行评价时，可以选用计算简单、反映经济指标或者物理变化过程的幅值裕度作为评价指标。

实时报警系统主要监视过程变量的参数值，一旦超过给定的报警阈值，立即触发报警。由于工艺的限制，不同工况下工艺参数的报警阈值不一样，可以设置成定值或者是与工况相联系的预先设定的变量。图1为报警设定值的参数关系，其中符号A代表在参数正常运行过程中扰动值和报警整定值之间的差值，B代表为了克服扰动带来的干扰，扰动值与采取保护动作定值之间的差值。

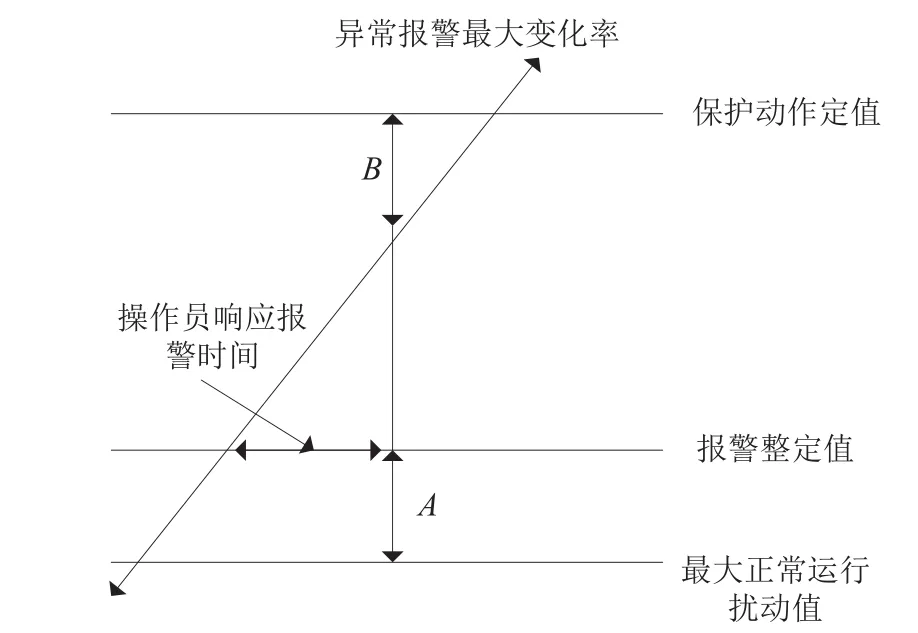
图1 报警整定值的设定

由于生产过程中报警的严重程度与产生的后果、变量的初始状态和工况条件等因素有关，因此报警系统应该充分考虑每一个报警变量的严重程度来对报警进行优先级划分。它的危害度函数的定义如下：

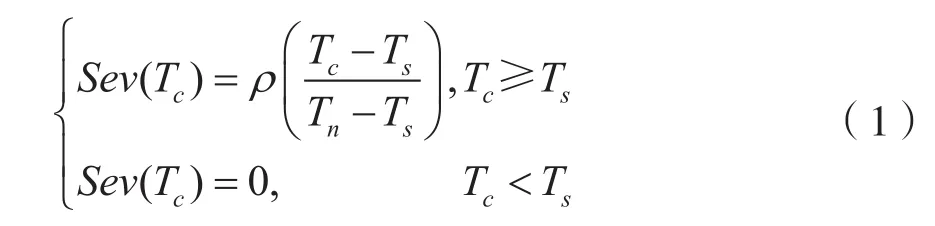
其中：Sev(Tc)表示每个报警的严重度，Tc为实时状态值，ρ为报警状态转移概率，Tn和Ts分别为报警的警戒阈值线和报警阈值线。幅值裕度指标不仅用概率的动态变化对报警进行分析，还考虑了状态的实时信息，指出了状态变量与最严重程度的偏离程度，对不同变量所处同一概率状态下的危害程度。

1.2 时间裕度指标

对于报警系统来说，超过报警之后有高报、高高报的情况下，为了更加明确报警状态的转移情况，在原有状态下增加几个安全报警状态，在变量的容许范围定义报警状态转移时间，分别为：正常状态（0）到低报警状态（1）的转移时T0→1=T1-T0；低报警状态（1）到中报警状态（2）之间的转移时T1→2=T2-T1；中报警状态（2）到高报警状态（3）之间的转移时 T2→3=T3-T2[16]。

根据定义的报警转移时间裕度，时间风险指标为：

图2为风险指标曲线，报警的风险值与时间有直接关系。报警状态转移时间越小，处理报警的时间越短，产生的后果也就越严重；报警状态转移时间越大，操作者处理报警的过程时间充裕，产生的风险也越小。

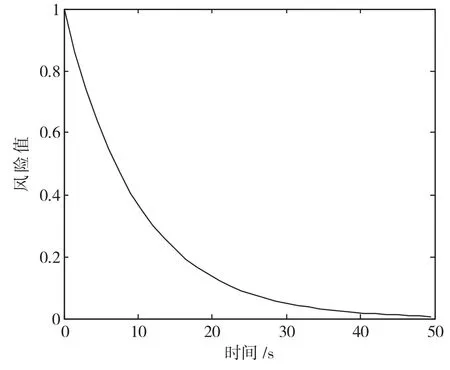
图2 风险指标曲线

2 基于Markov时变模型报警状态转移概率预测

2.1 建立马尔科夫时变模型

根据变量的历史数据和运行条件预测状态的发展趋势，结合幅值裕度指标中的报警状态转移概率，了解变量未来的某一时刻运行状态。

将Markov模型中，报警的状态空间分成（0，1，2，3）四种元素状态，其报警状态转移过程如图3所示。通过分析报警状态的转移过程的状态，进一步分析报警变量的危害程度，降低误报率和漏报率。报警状态转移的集合分别为：正常状态（0）的状态集合{0|x1,x2,…,xn0}到低报警状态（1）{1|xn0+1,xn0+2,…,xn1}、低报警状态（1）{1|xn0+1,xn0+2,…,xn1}到中报警状态（2）{2|xn1+1,xn1+2,…,xn2}、中报警状态（2）{2|xn1+1,xn1+2,…,xn2}到 高 报 警 状 态（3）{3|xn2+1,xn2+2,…,xn3}。由Markov过程确定的状态转移概率模型包括过程状态、转移概率和初始概率分布情况[17-18]。状态转移概率为：

表示时刻t处于状态i，经过时刻t+1处于状态j 的概率，初始概率用 π=[π1,π2,…,πn]来表示。

图3 报警状态网络空间转移过程

报警状态的转移规律可采用统计近似方法：

式中nij为从状态i转移到状态j的样本数，因此通过计算得到时刻t={0,1,2,3,…,m}，正常状态（0）、低报警状态（1）、中报警状态（2）和高报警状态（3）的状态概率转移矩阵pij(0:m)为：

根据马尔科夫无后性和贝叶斯条件概率公式，有：

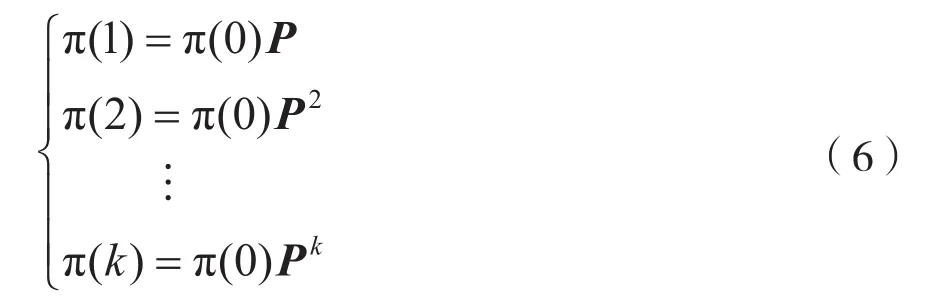
式（6）状态转移矩阵是不随时间变化的，而在实际工业过程中，状态转移矩阵是时刻发生变化的，因此需要根据系统实时变化的状态更新状态转移概率矩阵，从而更准确地估计风险状态：

式中，第k个时刻的状态为π(k)，由矩阵中最大的概率值确定当前的报警状态，其中状态转移矩阵P´的准确程度是最关键的因素。

2.2 粒子滤波估计动态状态转移矩阵

状态转移矩阵不能直接测量，通常是实验得到，因此存在很多不确定性。粒子滤波通过系统状态条件分布产生一组随机样本，然后不断调整修正粒子最初的条件分布。

假设P(xk(0))作为先验知识，那么P(xk(t)|yk(1:t))通过预测方程和概率的实时更新递推得到，然后利用最新得到的值对后验概率密度进行估计修正。

预测方程为：

更新方程为：

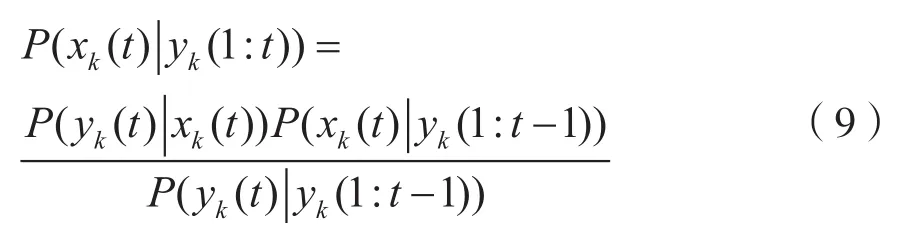
P(xk(t)|xk(1:t-1))由状态转移矩阵获得，P(yk(t)|xk(t))由预测方程获取。通过粒子滤波对预测方程和更新方程进行计算，计算得到状态转移过程的状态转移序列。它的状态转移序列的概率越大，代表下一时刻将要发生的情况。

假设变量的采样时间间隔为Δt，对于报警变量从时刻0运行到时刻m的时间转移过程的报警转移时间的计算可分别得到如下内容：

（1）r(tm)=0且r(tm+1)=1，系统从正常状态转移到低风险状态的报警转移时间为T0→1=m×Δt；

（2）r(tm)=1且r(tm+1)=2，系统从低风险状态转移到中风险状态的报警状态转移时间为T1→2=m×Δt-T0→1；

（3）r(tm)=2且r(tm+1)=3，系统从中风险状态转移到高风险状态的报警状态转移时间为T2→3=m×Δt-T1→2。

因此，通过已知的初始时刻和初始报警状态，利用式（7）得到第k时刻处于哪种报警状态空间（0，1，2，3）的概率情况，且得到处于不同报警状态空间的统计时间，综合发生的概率和时间对报警等级进行排序。

3 报警优先级评估计算

依据文中的报警幅值裕度指标和时间裕度指标，综合分析对报警优先级进行划分。流程如图4所示，分为离线训练和在线监测评价两个部分。

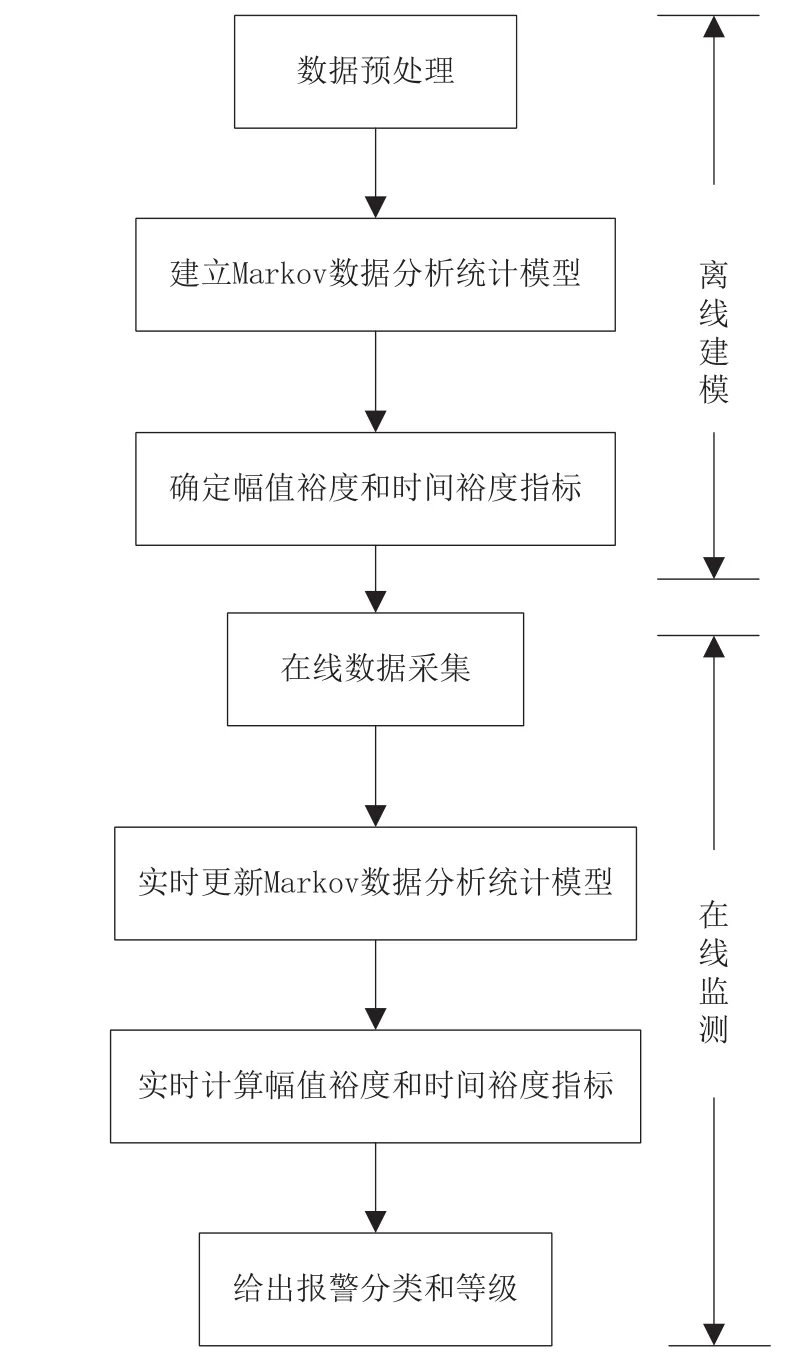
图4 报警优先级评估流程

离线部分：

（1）设变量的采样时间间隔为Δt，初始时刻为k=0，m=0；Δt=0所有的训练数据均正常，未发生报警事件；

（2）将历史数据作为训练数据，得到初始的状态转移矩阵；

（3）根据马尔科夫模型（4），得到各个状态发生的概率，并且估计报警状态的转移时间，由此得到报警状态的转移时间；

（4）根据式（1）和式（2），得到训练数据的报警等级指标；

（5）根据报警安全指标，得到报警等级的分类条件。

在线评价：

（1）当新样本到来时，计算新样本属于的报警风险状态，结合上一个报警状态，求取当前采样点的报警等级指标；

（2）判断所处的报警等级，计算当前的幅值和时间裕度，根据得到的裕度，预测下一时刻运行状态报警等级。

4 算例分析

以化工模型田纳西-伊斯曼（Tennessee Eastman，TE）过程为例。整个过程有6种操作模式和反应器、冷凝器、汽提塔、气液分离器及压缩机5个组成单元。化学反应方程式如下：

A(g)+C(g)+D(g)→G(liq)

A(g)+C(g)+E(g)→H(liq)

A(g)+E(g)→F(liq)

3D(g)+→2F(liq)

其中，A、C、D、E为4种所需的反应气体。当惰性气体B分别加入TE反应器中进行反应时，产物分别为液体G、H和副产品F。

选取数据库中5 500个采样数据进行分类划分，得到正常状态（0）、低报警状态（1）、中报警状态（2）和高报警状态（3），统计采集的各个时刻的状态数据转移次数，得到反应器进料流量结果如表2所示。

表2 反应器流量状态转移次数统计

根据统计结果计算状态的转移概率，得到的初始报警转移概率矩阵如下：

假设起始时刻都处在正常状态，初始状态的概率为π(0)={1,0,0,0}，将π(1)=π(0)P作为当前的状态概率。表3给出了传统的Markov状态转移变化结果。

表3 传统的Markov预测结果

由于工业现场环境非常复杂，外界干扰元素影响多，具有不确定性，其每一个变量的状态转移概率很难保持不变，是实时发生变化的，因此固定的状态转移概率不能反映真实情况，可以将转移矩阵更改为：

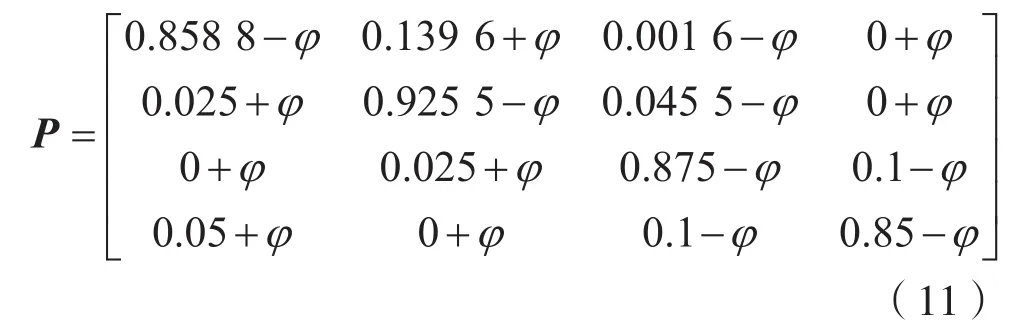
其中，φ=rand(0,1)为干扰变量，代表在区间[0，1]中产生的一系列随机数。为了更加真实地反映变量的状态情况，利用粒子滤波对变量的状态转移概率矩阵进行估计预测，可以得到动态的状态转移矩阵。图5和图6为采用3种滤波估计的仿真曲线图，通过对比不敏感卡尔曼滤波（Unscented Kalman Filter，UKF）、粒子滤波（Particle Filter，PF）和扩展卡尔曼滤波（Extended Kalmar Filter，EKF）3种方式对真实数值的估计曲线和误差曲线，得出粒子滤波具有更小的误差。

图5 报警状态转移矩阵估计

由于传统马尔可夫预测未能真实反映状态信息，导致预测结果和实际值有较大的误差。但是，通过粒子滤波估计状态转移矩阵的状态概率，使不确定性的转移概率具有较强的鲁棒性。其中，利用粒子滤波估计状态转移矩阵的状态概率如表4所示。

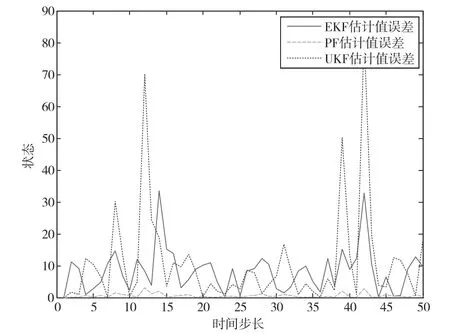
图6 估计误差

根据马尔科夫状态转移矩阵各个报警状态的概率值大小来确定危害程度，对得到的报警进行分类，确定当前时刻实际的报警状态是处在正常状态（0）、低报警状态（1）、中报警状态（2）和高报警状态（3）中的哪一类。

依据报警风险估计的预测结果，得到系统的报警风险状态转移时间分别为T0→1=m×Δt、T1→2=m×Δt-T0→1和T2→3=m×Δt-T1→2。对比各个报警状态转移时间的大小，可以得出处理变量的紧急程度。

利用上述方法，选择化工TE仿真模型中模式一中的反应器进料量进行评估，得到不同时刻的报警分类图，如图7所示。

表4 Markov时变模型预测结果

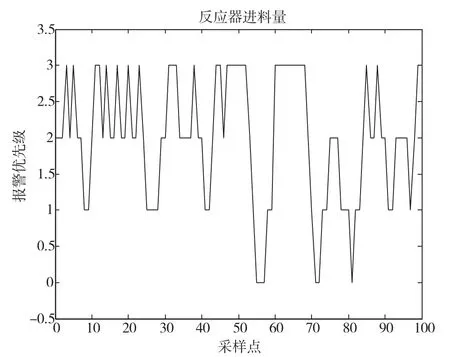
图7 反应器进料量报警状态

同理，图8、图9得到TE过程的反应器压力XMEAS8和反应器液位XMEAS9得到的变量报警图。如果变量所处的报警状态危害程度发生的概率相同，通过比较报警状态转移时间的大小来确定报警状态的处理的优先级。t=20时刻下报警优先级对比报警状态和转移时间得到同一时刻的报警排序结果，如表5所示。

图8 反应器压力报警状态

图9 反应器液位报警状态

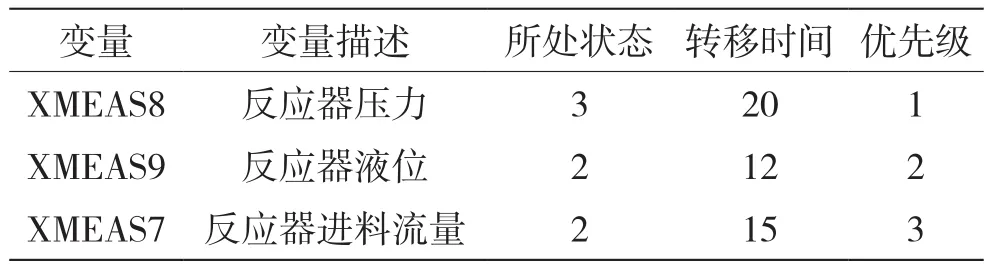
表5 t=20报警状态等级划分

5 结 语

报警分级评价模型能够帮助工厂操作者引起对重要报警的注意，而不需要在误报警和等级低的报警上花费更多时间。本文定义了量化报警风险的幅值裕度和时间裕度指标，考虑报警变量的危害程度和报警的转移时间建立报警优先级评估模型，综合评价处于不同状态的报警，以降低同时产生多个报警导致的重大损失。同时，考虑实际工况情况，降低外界不确定因素对变量的影响程度，利用粒子滤波估计Markov状态转移过程，预测报警状态变量的状态转移概率，实时预测反应状态变量的变化。通过化工TE过程算例的计算结果表明，提出的风险量化指标对报警状态的排序和对报警状态安全风险评估有一定的指导意义。由于报警系统的处理主要依靠专家经验，具有一定的主观性，在下一步的工作中，在实时报警等级管理系统中采用混合技术，通过自学习、自诊断修改模型来提高报警分类和预警的准确性。