基于时延的软件定义卫星网络控制域规划策略

2020-03-26郭子桢陈威龙陈金涛谢宝华

空军工程大学学报 2020年6期

郭子桢, 梁俊, 肖楠, 陈威龙, 陈金涛, 谢宝华

(空军工程大学信息与导航学院，西安，710077)

将软件定义网络架构引入卫星网络，能够使数据平面的卫星仅需承担转发和硬件配置功能，就实现路由策略的灵活部署、网络配置简化及网络成本降低[1]。随着卫星网络承载的业务越来越多，单个控制器显然无法满足网络的控制需求[2]，多控制器虽然能克服单控制器带来的单点失效和可扩展性差的缺点，却也带来了一个新问题：对于给定数量的控制器和交换机，如何合理规划交换机与控制器的配属关系。

现有SDN多域规划的研究已经较为成熟，能够为卫星网络相关研究提供一定的借鉴。WANG[3]等提出基于K-means的控制器部署方法，通过对网络中节点进行聚类，在聚类中心处部署控制器并按照跳数最少原则划分控制域，这能够有效降低控制器通信时延。文献[4]提出的K-Critical算法通过预测机制和多分类集网络拓扑构建，可以有效实现系统的负载均衡。文献[5]提出了一种自适应多域划分算法(Adaptive Multi-Domain Approach，AMDA)，通过考虑时延和控制器负载，采用谱聚类方法划分控制域。文献[6]提出了一种基于双向匹配的控制域划分策略，同时从控制器和交换机2个角度考虑，以实现控制器间的负载均衡。然而这些算法大多适用于拓扑固定且网络尺度较小的地面网络，将其直接应用于卫星网络会导致网络性能不理想。

目前，已经有许多研究者开始关注SDSN网络控制器部署问题：杨力[7]等提出一种基于双门限的控制器动态部署策略，通过定义控制器的负载状态以期实现控制器负载的动态调整，然而仿真实验却并未直接与卫星网络拓扑相结合。WU[8]等提出一种低开销的网络扩展方法，以控制器与交换机的最短距离为优化指标。XU[9]等借助STK工具对SDSN网络的时延进行了分析，将低轨卫星(Low Earth Orbit, LEO)按照轨道分组并从每组选出最靠近赤道且运动方向相反的2颗卫星部署控制器，共部署12个控制器，但这种部署方案要求星座中所有节点均安装控制器模块且动态调整其开闭状态，网络状态变化时的重规划开销过大。HU[10]等设计了一种SoftLEO架构，将LEO卫星按照轨道分为6组，选择6个纬度相近的节点作为每组卫星的控制器部署位置以减小控制器间的通信开销，然而网络的可靠性和负载均衡性能不够理想。WU[11]等设计了一种APSO算法全面的分析了控制器的状态同步开销、信息收集开销、流建立开销、网络重规划开销等并以此确定控制器部署位置。文献[12]通过线性规划优化流建立时延完成控制器部署及划域。文献[13]在部署控制器时将网络端到端时延和负载均衡指数作为优化目标。这些研究大多仅考虑传播时延，忽略了排队时延与处理时延，同时卫星网络中节点转发、处理能力有限，不同的负载将带来排队时延与处理时延的巨大差异进而影响划域结果，简单地忽略这些影响或者认为所有控制器都有相同的排队时延与处理时延的做法显然是不合理的，这将导致网络性能的下降。

本文针对现有算法时延描述不够全面的问题，综合考虑排队时延、处理时延、传播时延构建了软件定义卫星网络时延分析模型，并设计了基于模拟退火的多控制域均衡划分算法(Multi-Domain Balanced Partition Algorithm Based on Simulated Annealing, MDBPSA)，通过构建控制器匹配列表的方法寻找近似最优的划域结果，提升网络时延性能、实现网络负载均衡。同时由于卫星网络拓扑快速动态变化，时间片持续时间短，要求算法有较快的运算速度，本文特别设计了迭代跳出机制以加快模拟退火算法的求解速度，仿真结果表明改进后的算法求解时间远小于时间片持续时间且性能良好，能够满足卫星网络需求。

1 软件定义卫星网络架构

考虑到卫星地面站全球布站困难且成本高昂、同步轨道卫星(Geosynchronous Earth Orbit，GEO)处理转发能力无法适应LEO卫星数量和业务的快速增长、GEO卫星对地通信时延较大等问题[14-17]，本文采用在地面网络控制/监测中心(Network Control Center/Network Management Center, NCC/NMC)部署主控制器，在GEO卫星上部署区域控制器，并从基于OpenFlow的LEO卫星中挑选从属控制器的多层部署方案。该架构利用地面强大的计算能力和充足的存储空间控制整个网络，GEO卫星与地面站保持稳定连接，并选取从控制器作为GEO的补充。

整个SDSN网络根据GEO卫星数量及其覆盖区域划分为若干控制域，每个控制域包含一个域控制器、多个从控制器以及许多LEO卫星。每个控制域又被划分为若干个控制子域，每个控制子域内由从控制器管理其所属的LEO。运行过程中，GEO卫星接收流建立请求，并通过分发控制信息改变其控制域内的LEO状态。NCC/NMC访问LEO卫星，并通过GEO卫星管理整个网络，GEO卫星与NCC/NMC间的连接实现了全球流建立，能够对每一个控制动作做出响应。从控制器通过星间链路(Inter Satellite Links, ISLs)收集状态信息或将控制信息分发到所属子域内的LEO卫星。这种网络架构能极大地减少GEO卫星广播引起的干扰、控制器-交换机之间的信令延迟。下一步基于该架构对卫星网络中控制子域划分问题展开。

2 模型构建

SDSN控制子域划分问题可以运用图论相关知识进行描述。SDSN网络可以表示为G=(V,E)，其中V表示节点集合，E表示节点间链路集合。假设网络中所有LEO卫星均可承担交换机功能，其中的一部分部署了从控制器，LEO卫星数量为N，从控制器数量为M。从控制器集合用C={C1,C2,…,CM}表示，其处理能力为Ω={Ω1,Ω2,…,ΩM}，对控制器设置相应冗余因子βm∈(0,1)以预留部分处理能力预防过载[13]。LEO集合表示为S={S1,S2,…,SN}。两节点间最短路径表示为dmn。在卫星网络中网络流量可以表示为时间的函数，Sn在时间t内的流请求速率可以表示为λ(t)n。矩阵X描述SDSN控制域中从控制器和LEO的控制关系，其中元素取值见式(1)。

(1)

每个LEO仅与一个从控制器建立控制关系。因此整个控制域可划分为M个控制子域: Domainm1～DomainmM。

现有OpenFlow交换机均为多核交换机，且OpenDaylight、Ryu等控制器均采用多线程处理方式，因此，可将LEO与从控制器间的通信过程近似为G/M/k排队模型，即消息到达为一般过程、控制器对于流请求的处理为马尔科夫过程、从控制器线程数为k。在此基础上，可计算相关参数。

2.1 LEO到从控制器时延

所有与Cm相连的LEO的流请求速率之和即为Cm在时间t内需要处理的流请求，记为L(t)m，见式(2)，其中各LEO交换机之间的流请求相互独立。

(2)

由Little原理可得流请求排队时延Q(t)m，见式(3)。

(3)

式中：Ω(t)m表示时间t内从控制器Cm的可用处理能力，且0<Ω(t)m<Ωm；λ(t)mn表示Sn在时间t内对Cm的流请求速率。

Cm的平均处理时间为P(t)m，满足：

(4)

卫星网络覆盖范围大，路径传播时延也是控制子域规划的重要指标。传播时延T(t)m满足式(5)：

(5)

(6)

则控制子域内LEO到从控制器平均时延：

AT(t)m=Q(t)m+P(t)m+T(t)m

(7)

控制域平均时延为AT(t)：

(8)

2.2 网络开销

SDN架构下无法匹配流表的数据包需上交从控制器处理，且从控制器需要进行周期性通信以更新控制逻辑，保持控制域内网络视图。因此网络开销主要可分为转发开销和状态同步开销2个主要部分。转发开销PT主要为从控制器处理LEO的Packet-in包并下发流表所带来的网络开销，见式(9)。状态同步开销PS见式(10)。

(9)

式中：vR为从控制器轮询LEO的平均速率。

(10)

式中：vS为从控制器状态信息的平均传播速率。网络开销即为转发开销与状态同步开销之和。

TL(t)=PT+PS

(11)

2.3 目标函数

为了合理地配属从控制器和LEO之间的匹配关系，尽可能减少从控制器和子域内LEO之间的平均时延且控制网络开销。因此，得到如下目标函数：

目标函数及约束条件：

minObject=[yAT(t)+(1-y)TL(t)]

(12)

∀m,L(t)m≤βm·Ω(t)m

(13)

(14)

式中：y∈(0,1)，用于调节平均时延和网络开销对于控制域规划的影响。

上述约束条件中，式(13)表示网络中没有控制器过载的情况发生。式(14)表示所有LEO都只能连接到唯一一个从控制器。

3 算法设计

3.1 匹配机制设计

定义1匹配。即LEO与从控制器建立控制关系。例如Sn若受Cm控制，则LEO与Cm完成匹配。记为(Cm，Sn)。

定义2从控制器匹配列表。从控制器将控制域内所有LEO按照dmnλ(t)n升序排列，并构造匹配列表Γ(Cm)={Sn,…}，在从控制器未过载的情况下优先与匹配列表中排序靠前的LEO建立匹配。

定义3优选。若Sn在从控制器匹配列表Γ(Cm)={Sn,…}中排在首位，则Sn是Cm的优选LEO，记为Sn←Γ(Cm)。

3.2 基于模拟退火的多控制域均衡划分算法

MDBPSA算法的基本流程为：首先收集网络历史状态信息，由于卫星轨道的周期性，我们能够获得所需信息作为划域依据。匹配过程中从控制器在处理能力允许的情况下，优先与优选LEO进行匹配。针对栅格化的卫星网络使用鲁棒性强的模拟退火算法对从控制器与LEO的匹配进行优化，寻求使目标函数最小的匹配方式。不断重复该过程，直至网络中不存在未得到匹配的LEO，得到SDSN多域划分。

表1 基于模拟退火的多域均衡规划算法

建立匹配时，LEO向所有从控制器提交匹配申请，各从控制器匹配列表中元素相同，只有排序的差异。在匹配过程中若存在从控制器不满足L(t)m>βmΩ(t)m|Ω(t)m≤0，则采用模拟退火算法为不满足条件的从控制器建立匹配，并将建立了匹配的LEO从匹配列表中剔除。若所有从控制器均满足L(t)m>βmΩ(t)m|Ω(t)m≤0，则放宽匹配条件，为仍未得到匹配的LEO选择可用处理能力最大或过载程度最轻的从控制器建立匹配，直至匹配列表为空集。综上，在整个匹配过程中不会遗漏任何LEO，能够为每个LEO选取合适的从控制器建立匹配关系。

4 仿真与性能评估

4.1 仿真环境建立

4.1.1 实验工具

实验利用STK11.01工具进行卫星轨道的相关仿真并借助Matlab2016b工具对算法进行仿真和分析实验结果。

4.1.2 拓扑选择

实验拓扑以IRIDIUM[18]进行调整得到，如表2所示。这样可使得时间片划分个数少于644个，最短持续时间大于8 s，平均持续时间大于133.17 s[19]，为控制域规划留出了充足的时间。

表2 卫星轨道参数设定

4.1.3 仿真参数设定

本文仿真参数设定如下：差异化的选取LEO流请求速率λ(t)n的值，将取值范围设定为100～500 kB/s以模拟卫星网络控制流量特征。从控制器处理能力均为8 MB。设定从控制器冗余因子为0.9，轮询LEO的平均速率为vR=10 kB/s，进行状态同步的传播速率vS=1 kB/s。y值设定为0.5。

4.2 仿真结果分析

4.2.1 算法运算时间

为了缩短模拟退火算法运算时长以适应卫星网络拓扑变化，MDBPSA算法设计了迭代跳出机制以缩短算法运行时间。模拟退火算法的特点是能够依概率接受较差的解，避免陷入局部最优。因此设置计数器记录新解被拒绝的次数，若连续k次被拒绝，则提前结束本次迭代。k与目标函数值及算法运算时间的关系如图1所示，将相同条件下重复实验50次的最优值作为最终结果。图中红色虚线为不设置迭代跳出机制时Object极限值，此时的运算时间为10.27 s。

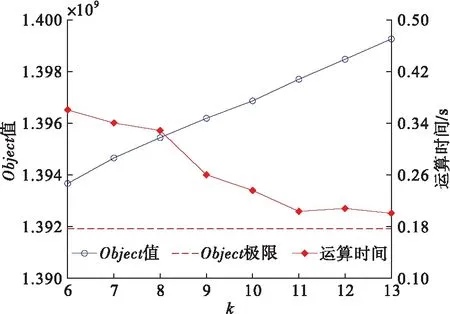
图1 Object值、运算时间与k的关系

由图1可以看出，k=11时能够在保证求解结果良好的情况下尽可能缩短算法运算时间。此时算法运算时间的累积分布函数如图2所示，可知运算时间基本保持在0.56 s之内，较时间片最短持续时间小很多。迭代跳出机制能够明显加快算法运算速度，使得算法能够适应卫星网络拓扑的快速动态变化。

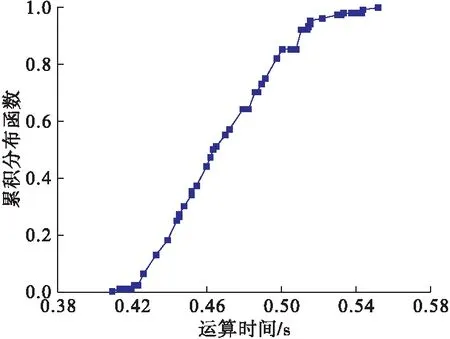
图2 算法运算时间

4.2.2 子域划分

为了展示MDBPSA算法的控制器负载均衡性能，后续实验将地面网络中较为成熟的AMDA方法[5]及文献[12]划域思想(下文简称为ILP方法)作为对比。AMDA算法按照负载自适应方式为控制器动态分配交换机完成多域构建；ILP方法力求使网络流建立时延最小。以控制域网络拓扑为仿真对象，其中共包含25个LEO节点及40条星间链路。假设网络中所有节点间统计相互独立且都具备部署从控制器的能力，将其中4个节点设置为从控制器节点，使用不同方法对上述网络拓扑进行子域划分，结果如图3所示。图中以不同形状区分LEO节点及从控制器节点，C1～C4所管理的控制子域Domainm1～Domainm4分别以白色、浅绿色、深绿色、黑色表示。

图3 多域规划结果

3种划域方式控制子域负载对比见图4。

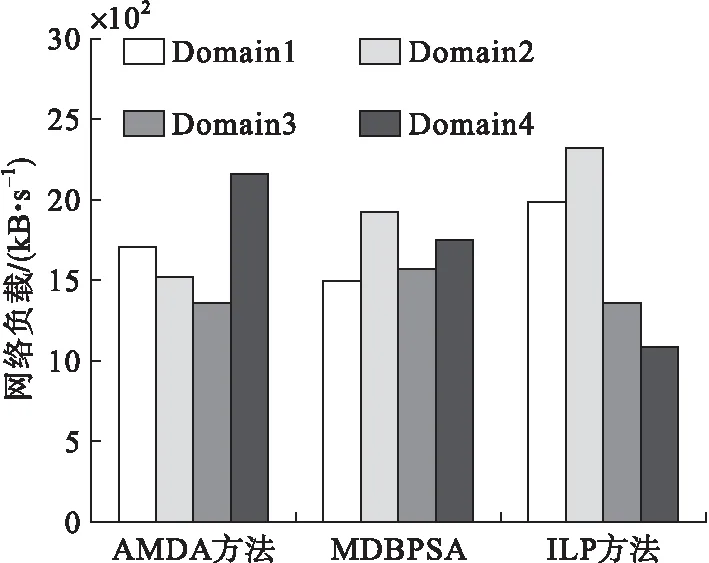
图4 网络负载对比

从图4可以看出ILP方法从控制器负载差异最大，这是由于该方法将流建立时延作为优化目标，仅考虑传播时延而忽略了控制器处理能力限制，这也说明了在卫星网络中部署控制器时不考虑处理时延和排队时延的做法不够合理。AMDA方法和MDBPSA均实现了LEO与从控制器的均衡连接。相较而言，MDBPSA加入了对处理时延的考虑，且网络时延由各控制子域时延按负载加权得到，加强了对网络负载的限制，故能取得更好的负载均衡性能。以从控制器负标准差作为衡量划域均衡性的指标，可得到如下结果：AMDA方法297.039、MDBPSA算法168.158、ILP方法492.446，可以看出MDBPSA算法负载均衡性明显优于其他算法，较AMDA方法提升43.39%，较ILP方法提升65.85%。

4.2.3 LEO到控制器平均时延及网络开销

在实验2所得子域划分的基础上，本实验对3种方法LEO到从控制器时延进行对比。实验中假设数据包在星间链路传播时速率稳定可靠且丢包率为零。图5为3种算法的控制域平均时延情况。

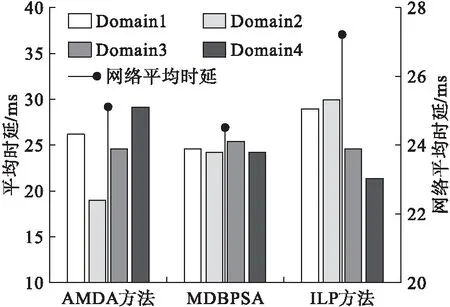
图5 平均时延对比

从图5可以看出，MDBPSA算法各子域的平均时延相差不大，而AMDA方法中Domain4和ILP算法Domain2的平均时延很大。这是因为AMDA作为一种弹性规划方式，虽然能够快速的均衡从控制器负载，但从控制器与LEO之间的连接关系并不稳定，不稳定的网络关系导致部分从控制器平均时延增大。在更为复杂的网络环境下这种现象更加明显，甚至可能引起跨域通信问题使网络时延急剧增加。而ILP算法缺乏对控制器处理时延、排队时延的考虑，导致时延性能不够理想。综合来看，MDBPSA 算法将排队时延和处理时延纳入考虑范围后能够明显平衡各控制子域时延，使网络平均时延低于AMDA方法且较ILP方法降低约10%。

图6为3种方法的网络开销情况。

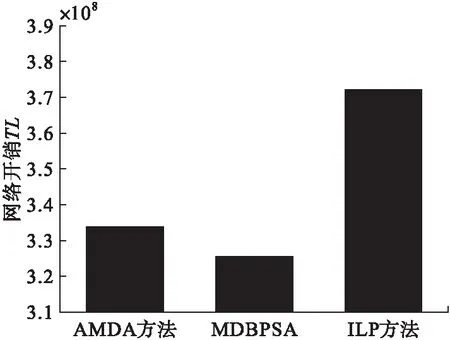
图6 3种方法网络开销对比

由图6可以看出MDBPSA算法在具有较好性能的同时，网络开销也低于对比算法。这是由于AMDA方法、ILP方法分别注重负载和流建立时延而对控制器到交换机距离缺乏关注故而性能并不理想。通过对算法的分析可知，MDBPSA算法在进行划域时对节点间距离与流量负载情况均进行了考虑，而网络开销主要与节点间距离及流量负载情况有关，故而MDBPSA算法能够使网络开销较ILP方法下降12.52%。