样本缺失情况下的雷达目标自适应检测

邹 鲲， 来 磊， 骆艳卜， 李 伟

(空军工程大学信息与导航学院， 西安， 710077)

雷达信号检测在数学上属于统计假设检验问题，检测性能与数据的统计模型密切相关[1]。然而在雷达检测器设计阶段，目标背景噪声(包含了杂波、热噪声和可能的干扰)统计特性往往是未知的，需要一定数量的参考数据，用于待检测单元背景噪声的抑制和目标的检出，这种检测手段称为自适应检测[2]。对于雷达目标检测问题，基于奈曼皮尔逊准则的一致最大势检验通常不存在[3]，可以依据其他不同的准则设计不同的自适应检测算法。例如采用广义似然比检验(Generalized Likelihood Ratio Test, GLRT)准则可以得到GLRT检测器[2]和自适应匹配滤波器(Adaptive Matched Filter,AMF)[4]，利用Wald检验准则[5]和Rao检验准则[6]也可以得到对应的检测器。这些检测器都是渐近最优检测器，在参考数据较少的情况[7]或导向矢量失配[8]时，检测性能会出现差异。

自适应检测的性能与参考数据数量、质量密切相关。为了更好地抑制待检测单元背景噪声，参考数据的数量必须足够多，且参考数据与待检测单元背景噪声的统计特性一致，即所谓的场景均匀性。在均匀场景中，参考数据数量必须大于检测问题维度的2倍时，GLRT的检测性能损耗才能控制在3 dB以内[2-3]。然而在实际情况下，对参考数据的数量和质量的要求往往很难得到满足。例如在雷达空时自适应处理过程中[10]，检测问题维度是空时2个维度的乘积，且探测环境也受地物分布、复杂电磁环境的影响，很难找到满足要求的参考数据。因此针对非均匀场景、干扰条件下的自适应检测问题[11-19]是当前的一个研究热点。

本文考虑参考数据中部分样本缺失问题，其也可以作为一种特殊的非均匀场景。造成样本缺失的原因可以来自功率较强的干扰设备[20]，导致雷达接收数据中部分信号幅度值超过了接收机最大动态范围，从而被标注为无效数据；也可以来自雷达系统内部设计的缺陷，某些数据处理不及时导致的样本丢失[21]。常规的处理方法是将缺失的数据置零或进行插值，但都会导致参考数据的统计特性出现偏差，影响了自适应检测性能。为此，本文首先提出了基于期望最大算法的自适应匹配滤波器(Expectation Maximization Based Adaptive Matched Filter, EM-AMF)。

1 检测问题

考虑如下的自适应检测问题：

(1)

在这个检测问题中，待检测单元数据z0是长度为N的复矢量，在H0假设下仅仅包含背景噪声分量y0，其服从均值为0、协方差矩阵R未知的复高斯分布，而在H1假设下，待检测数据中叠加了一个幅度α未知的信号导向矢量v。为了估计杂波协方差矩阵R，假定还存在数量为K的参考数据zk,k=1,2,…,K，这些数据仅仅包含了背景噪声分量yk，其与待检测单元背景噪声分量y0为独立同分布。采用N维矢量pk，表示第k个参考数据部分样本缺失情况，数据缺失表征矢量pk中的每个元素取值0或1，如果是1表示该数据是正常的，如果是0表示该数据是缺失的，那么接收信号zk可以表示为pk与yk的Hadamard乘积，用符号⊙表示。本文假定数据缺失表征矢量pk是已知的。

自适应匹配滤波器(AMF)是基于双步GLRT检验准则得到的，其形式[4]为：

(2)

(3)

2 基于EM算法的自适应匹配滤波器

利用数据缺失表征矢量pk，将每个参考数据yk划分为2个部分：用yk,obs表示可观测的数据，是由yk中可观测分量构成的集合；yk,mis表示缺失的数据，是由yk中不可观测分量构成的集合，其中的下标表示为集合：

(4)

由此EM算法表示为[22]：

R(n+1)=arg maxR·

(5)

式中：R(n)表示协方差矩阵R的第n次迭代估计值。可以看出，EM算法包含了2个步骤：①计算条件似然函数的期望；②计算R使得期望最大化。

在EM算法的期望步骤中，考虑到：

yk={yk,obs,yk,mis}|R～CN(0,R)

(6)

式中：符号～表示服从某种分布；CN表示复正态分布的缩写。对数似然函数可以表示为：

lnp(yk,obs,yk,mis|R)=

(7)

式中：c表示常量；符号‖ ‖和tr{ }分别表示矩阵的行列式和迹。依据式(5)，需要对式(7)计算条件期望。利用条件高斯定理[23]可以得到：

(8)

其中：

(9)

式中：R[a,b]表示N×N矩阵R中由集合a构成的行和集合b构成列组成。将式(7)代入到式(5)中，并利用式(8)和式(9)的结论，可以得到:

Eyk,mis|yk,obs,R(n){lnp(yk,obs,yk,mis|R)}=

(10)

其中：

(11)

EM算法的步骤②可以表示为：

R(n+1)=arg maxR·

(12)

容易得到：

(12)

EM算法是一种迭代算法，因此首先可以设置一个协方差矩阵的初始值R(0)，分别计算式(9)、式(11)和式(13)完成对协方差矩阵的更新估计，并计算：

f(n+1)=

(13)

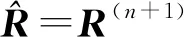
3 基于MCMC方法的自适应匹配滤波器

在雷达目标检测过程中，关于待检测单元杂波协方差矩阵，如果有一定的先验信息，就有可能提升检测性能。先验信息的使用在贝叶斯框架下，可以用先验分布表示。为此假定假设检验问题(1)中，R的先验分布为复逆Wishart(Complex Inverse Wishart, CW-1)分布，即R～CW-1(v0,(v0-N)R0)，其概率密度函数可以表示为：

etr{-(v0-N)M-1R0};v0≥N+1

(15)

(16)

CW-1分布参数R0表示了先验均值，而参数v0表征了对这个先验均值的不确定性。v0越大，CW-1分布更加集中在其均值R0处，说明不确定性较低，反之当v0=N+1时，表示不确定性最大。需要指出的是，这里采用CW-1分布作为协方差矩阵R的先验分布的原因是，对于复高斯分布的协方差矩阵，其共轭先验分布是CW-1分布，即先验分布与后验分布具有相同的形式，有利于简化计算。为此利用式(6)，容易得到R的后验分布：

f(R|y1…yk)～

(17)

E(R|y1…yk)=θY+(1-θ)R0

(18)

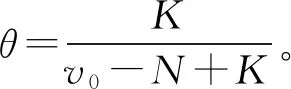
Gibbs抽样方法是MCMC仿真手段的一种，其通过构造参数的后验分布，得到抽样样本的马尔科夫序列，只要序列足够长，该序列统计分布最终可以收敛到目标分布。给定一个协方差矩阵初始值R(0)，利用式(8)，可以产生一个随机矢量yk,mis，将其与观测矢量yk,obs一并构成参考数据yk。再利用式(17)，可以随机产生一个协方差矩阵R(1)。由此可以得到一个协方差矩阵的马尔科夫序列R(n)，n=1,2,…,N。计算这个序列经过收敛之后的均值，作为杂波协方差矩阵后验均值的估计：

(19)

式中：N表示Gibbs抽样得到的样本总数；Nb表示当抽样迭代次数达到Nb时，获得的样本分布收敛到了目标分布。

4 数值仿真分析

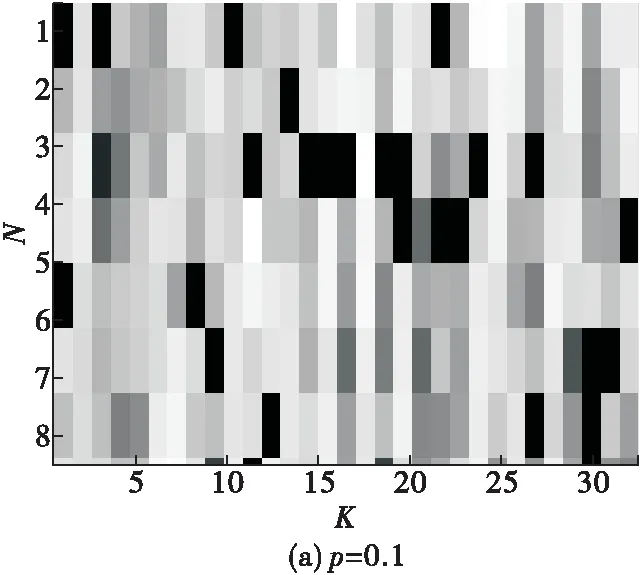
图1 存在样本丢失的参考数据(N=8,K=32)

4.1 Gibbs抽样收敛性能分析

对于Gibbs抽样算法，首先要确定协方差矩阵序列R(n)在什么时候开始处于收敛状态，即式(19)中Nb的取值。为此本文采用势尺度(Potential Scale, PS)的概念[25]进行数值分析。依据指定的先验分布参数v0和R0，利用式(15)随机生成一个初始值R(0)，利用Gibbs抽样算法，可以得到一个抽样矩阵序列R(n)，n=1,2,…,L。选择序列中每个矩阵的第m行第n列的元素进行分析，其可以构成一个标量序列φ(n)。将这个序列定义为一个长度L的列矢量φ。将这个过程重复M次，由此可以得到M个长度为L的序列，φ1,φ2,…,φM。分别计算每个序列的均值、方差和所有序列的均值：

(20)

再计算序列间(Between-Sequence)方差B和序列内(Within-Sequence)方差W：

(21)

那么势尺度定义为：

(22)

序列的收敛性主要分析势尺度因子与1的距离，越靠近1说明序列越接近目标分布。

图2给出了势尺度与迭代次数之间的关系，这里选择v0=N+1，R0=IN，即单位矩阵。独立运行次数M=500后进行平均。可以看出，采用Gibbs抽样方法获得的马尔科夫序列最终都会收敛到目标分布，但收敛速度与参数K和丢失样本占比p有关。K值相同时，丢失样本越多，收敛的速度越慢。丢失样本占比p相同时，K越大，收敛速度越慢。

图2 Gibbs抽样算法收敛性能分析

4.2 检测性能对比分析

将AMF作为检测器结构，指定虚警概率为10-3，利用计算机仿真获得判决门限。分析不同的信噪比条件下的检测性能。信噪比SNR定义为：

SNR=|α|2vHM-1v

(23)

作为对比分析，将匹配滤波器MF作为检测性能的上限，即假定杂波协方差矩阵已知。还可以对存在样本缺失的参考数据zk进行线性插值，将插值后的数据用于计算样本协方差矩阵，并代入式(2)中，得到的检测器标记为LI-AMF。

而对于MCMC-AMF检测器，其先验分布参数设置为v0=N+1，R0=IN，这种参数设置表示对协方差矩阵的先验信息较少。另外一种设置为v0=N+8，R0(m,n)=0.8|m-n|ej2π(-0.15)(m-n)，这种参数设置表示对协方差矩阵有一定的先验信息，但先验均值与实际的M取值存在少许差异，v0的值取得更大一些，表示对该先验信息的把握程度更高一些。由此得到的检测器标注为MCMC-AMF(Info)。

图3给出了p=0.1时的检测性能，分别考虑K=12和32。

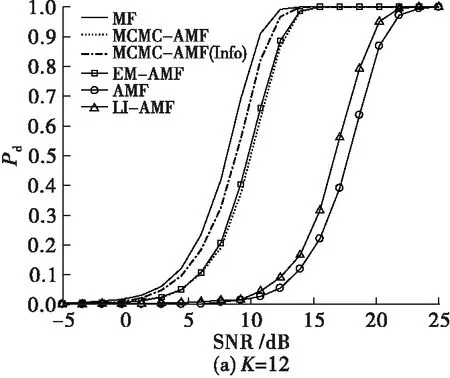
图3 检测性能(p=0.1)

首先可以看出，MF的检测性能可以作为所有的检测性能的上限，而AMF的检测性能可以作为下限。这是因为参考数据中存在数据缺失，直接影响了检测性能。通过对缺失数据的插值，LI-AMF的检测性能相对AMF有了略微的提高，但是由于这种插值方法忽略了信号本身的统计特性，对检测性能的提升是非常有限的。本文提出了MCMC-AMF和EM-AMF具有较好的检测性能，且性能相当。这是因为这两种方法都没有使用协方差矩阵的先验信息，如果使用先验信息，MCMC-AMF(Info)的检测性能可以得到进一步的提高。这种提高程度在K较小的情况下更为明显，这是因为参考数据数量的增加可以弥补先验信息的缺失。

进一步将数据缺失比例因子设置p=0.3，检测性能见图4。

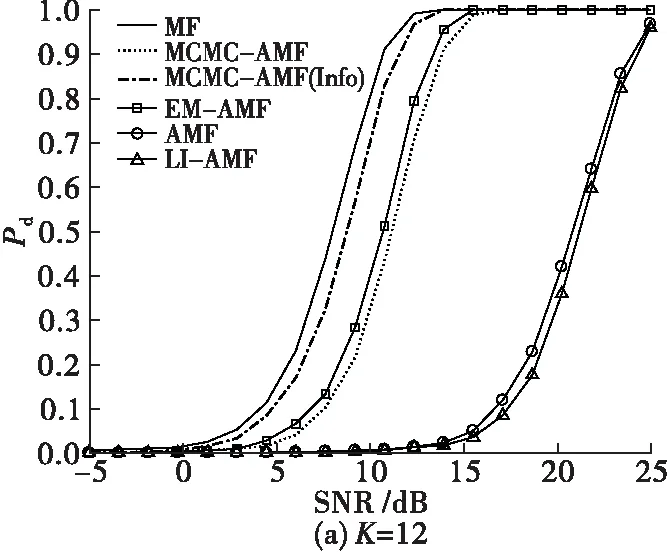
图4 检测性能(p=0.3)

此时参考数据中数据丢失的个数增加，直接从参考数据中获取杂波协方差矩阵的信息进一步降低，因此此时的AMF和LI-AMF的检测性能会进一步降低。MCMC-AMF和EM-AMF的检测性能也会受到影响，K=12时，与图3(a)对比出现一定程度的下降，但下降程度不太明显。而对于K=32时，检测性能受到p的影响较小，这还是因为参考数据的增加在一定程度上可以弥补数据样本丢失导致的信息损耗。同样，利用先验信息，MCMC-AMF(Info)的检测性能可以得到进一步的提高。

5 结语

在复杂电磁环境中，各种可能的干扰会导致雷达接收数据中个别样本丢失，如果不加以处理，或仅仅是简单的插值处理，检测性能往往会受到严重的影响。本文提出了基于EM算法和MCMC仿真的2种杂波协方差矩阵估计方法，如果关于协方差矩阵的先验信息较少，采用EM算法和采用MCMC仿真方法得到的检测性能是相当的。如果可以采用协方差矩阵的部分先验信息，即便先验信息不够准确，仍然可以有效提升检测性能。