热压罐成型过程中框架式模具温度场模拟与分析
2020-03-26安鲁陵花蕾蕾岳烜德匡海华
熊 蓉 安鲁陵 花蕾蕾 岳烜德 匡海华
(1 南京航空航天大学机电学院,南京 210016)
(2 高性能电磁窗航空科技重点实验室,济南 250000)
文 摘 为了研究复合材料构件成型模具温度场,本文以某型飞机壁板的热压罐固化工艺为例,通过模型简化,利用FLUENT 等仿真软件建立模具温度场的数值模拟模型,并将模拟数据与实验数据进行对比。结果表明二者平均相对误差为7.4%。此外通过仿真模拟一组以支撑板厚度为变量的实例,两组以U、V 两个方向的支撑板厚度为变量的对照组,通过判断模具型板表面温度方差大小,研究了支撑板厚度对模具温度场分布的影响规律。结果表明,模具温度场的均匀性随着支撑板厚度的增加而逐渐降低,其中U 向支撑板厚度的变化对温度场均匀性的影响比V向大。
0 引言
复合材料的比强度和比模量大、疲劳寿命长,这些优点使其在航空航天等众多领域有逐渐取代传统金属材料的趋势[1]。
热压罐成型工艺是目前最常用的整体成型复合材料构件技术[2]。热压罐中的复合材料构件在固化过程中,成型模具温度场的不均匀性会导致其产生固化梯度[3],从而引起残余应力和变形,成型的构件可能会出现气泡等的质量问题[4]。因此研究复合材料构件成型模具温度场具有重要意义。
在国内外各种对模具温度场模拟的研究中,G.N. Xie 等[5]考虑了强制对流现象等因素后建立了模具温度场的仿真模型,并引入了两个无量纲因素来评价模具温度分布的均匀性。王永贵等[6]研究了热压罐成型工艺过程中的热量传递路径等,通过对比实验和仿真数据,得到了框架式模具的温度场分布特点。白光辉等[7]建立了某真实复合材料加筋壁板的框架式模具温度场的精化模拟模型,最终结果表明模拟精度能够达到10%。
国内外的学者对成型模具结构的改进也做了很多的研究。J.L.Gniatczyk 等[8]提出采用“蛋盒式”框架结构可以提高模具的导热性。C. N. Michael 等[9]研究了空气热通量方向和“蛋盒式”框架结构模具对传热系数的影响,最后建立了传热系数的精确预测模型。张旭生等[10]采用CFD 方法对3 种风道不同的框架式模具进行了研究,研究结果显示T型风道对于改善温度均匀性的效果最好。林家冠等[11]提出在型板背面的通风孔处安置排风扇可以打散原有的漩涡,提高传热效率,有利于型板表面的温度均匀性。
本文以某型飞机壁板的热压罐固化工艺为例,建立数值模型分析模具温度场的分布,采用温度方差作为温度均匀性的判断参数,进而对模具支撑结构进行改进研究。
1 数值模拟
FLUENT是功能强大的CFD软件,它包含的物理模型和数值计算方法多样,计算精度和效率高。因此本研究采用其作为模拟模具温度场的工具。
1.1 基本控制方程
1.1.1 流体区域
热压罐内的流体流动和传热现象均受质量、动量和能量守恒定律的支配,在进行仿真时需将这些定律作为数值模拟的基本控制方程。在笛卡尔坐标系中,这些方程表示如下[4]。
(1)质量守恒方程
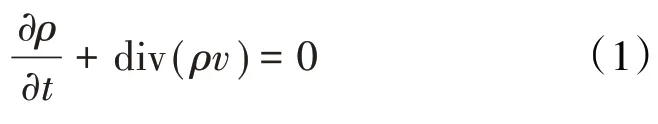
(2)动量守恒方程
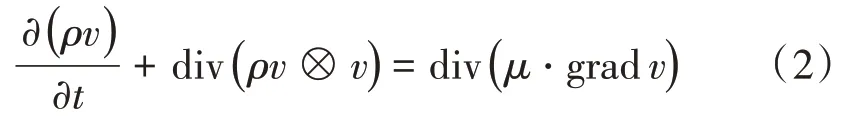
式中,ρ是流体密度,μ是动力黏度,p是流体压力,v是流体速度,S是广义源项。
(3)能量守恒方程
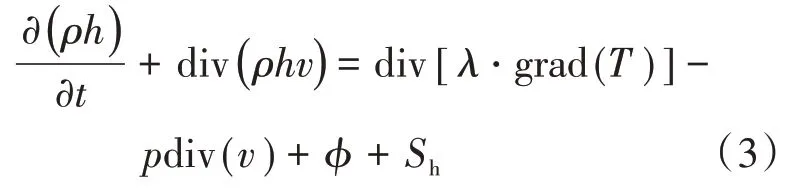
式中,h=h(p,T),λ是流体热导率,φ是由于粘性作用机械能转换为热能的部分,Sh是内部热源。
(4)状态方程

1.1.2 固体区域
能量守恒方程可以写成:
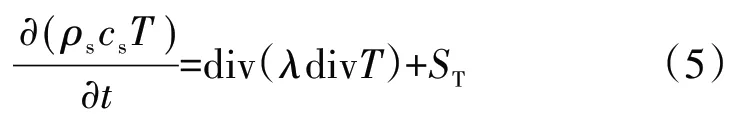
式中,ρs是固体密度,cs是固体比热容,T是固体温度,ST是固体内部热源项。
1.2 模型简化与网格划分
采用的框架式模具的几何模型如图1所示,尺寸为2 040 mm×1 140 mm×500 mm,材料为Q235。型板厚度为12 mm,表面为光滑双曲面。底部为7×3 的厚度为10 mm 的支撑板,板上采用散热孔和通风孔,加强空气流动。参照实际研究对象,根据热压罐内腔将其简化为一个Φ3 m×6 m的圆柱体。
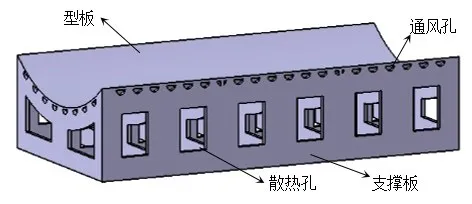
图1 成型模具简化结构Fig.1 Simplified structure of the forming mold
在进行仿真之前需要进行网格划分,因模具结构较为复杂,因此采用ICEM 进行非结构化网格的划分,在数据变化剧烈的区域进行加密,其他区域采用尺寸较大的网格,最终结果如图2所示。

图2 网格划分结果Fig.2 Meshing results
1.3 湍流模型与边界条件
热压罐中的热交换方式以强迫对流换热为主,在建立有限元模型的过程中,需要考虑流体流动状态。根据传热学理论,流体流动类型可通过雷诺数Re的大小进行判断:
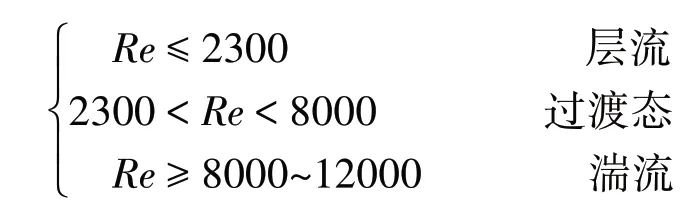
雷诺数的表达式如下:

式中,L为管道直径,u为流体流速,ρ为流体密度,μ为动力黏度。
表1列出了用于计算流体雷诺数的参数值。

表1 流体状态判断参数值Tab.1 Parameter value for fluid state judgment
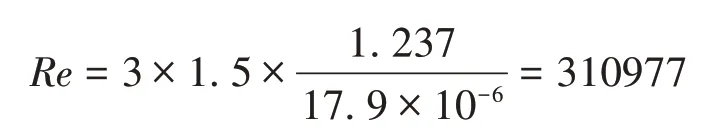
由计算得到的雷诺数可判定罐内空气流动状态为湍流。目前最广泛应用于实际的湍流数值分析方法是将三维非稳态Navier-Stokes 方程变化为时间平均方程,应用该方法后方程的个数少于变量个数,需要同时添加湍流模型。湍流模型分为应力模型和涡粘模型,涡粘模型下又有零方程模型、单方程模型[12-13]和两方程模型[14-15],两方程模型下有标准K-e模型等。由于雷诺数较高且标准K-e 模型的精度和效率表现得较为均衡[16],因此采用标准K-e模型。
按照热压罐的操作工艺设定边界条件如下。
(1)将圆柱体(热压罐)的一端面设置为速度入口,风速为1.5 m/s,水力直径为3 m,湍流强度为5%。利用FLUENT 的UDF 功能编写子程序,针对复合材料,设置固化工艺温度曲线如图3 所示,整个过程经历30 240 s结束。
(2)另一端面设置为压力出口,压力为静态压力,大小为内腔的工作压力。
(3)壁面设置为WALL。

图3 固化工艺温度曲线Fig.3 Curing temperature curve
1.4 模拟结果
图4为在不同的升温、保温和降温阶段的温度云图。由图4可见,型板表面的温度呈明显的阶梯状分布,温度从迎风端到背风端逐渐减小。经过分析,产生这种现象的原因是:(1)强迫对流换热是热压罐内主要的热交换方式,当空气流经模具的型板表面时,靠近表面的气体会形成温度边界层。由于气体的粘性作用,边界层的速度沿着空气的流动方向逐渐减小,厚度随之增加[17]。由于热阻随着边界层厚度的增加而增大,沿着流向,热阻逐渐变大,导致型板表面的温度呈阶梯状分布;(2)由于迎风端的支撑板对空气的阻碍作用,背风端的支撑板对型板的传热效率较为低下,导致背风端温度较低。
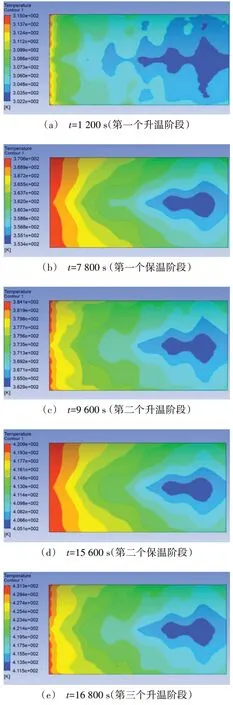
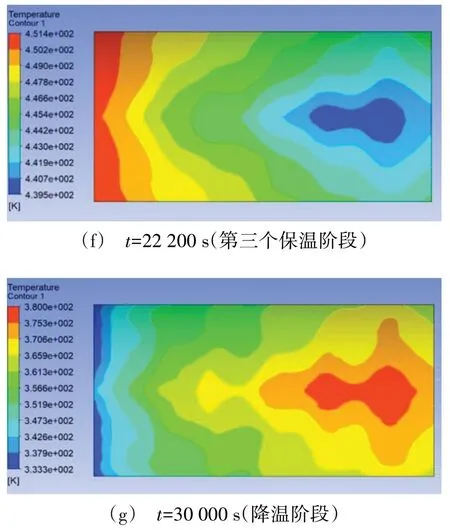
图4 不同阶段的温度云图Fig.4 Temperature map of different stages
2 验证实验与对比分析
2.1 验证实验
实验装置如图5所示,实验所用的热压罐和模具均与仿真时相同。实验过程中,空气流速为1.5 m/s,空气温度随时间变化的规律同前述的固化工艺温度曲线一致。在型板表面布置12个热电偶采集实验数据,热电偶的分布位置如图6和图7所示。12个热电偶每隔120 s 同时采集各个点的温度数据,直至30 240 s固化过程结束。

图5 验证实验模具及热压罐Fig.5 Verification test mold and autoclave

图6 型板表面热电偶布置位置Fig.6 Placement of thermocouples on the surface of the plate
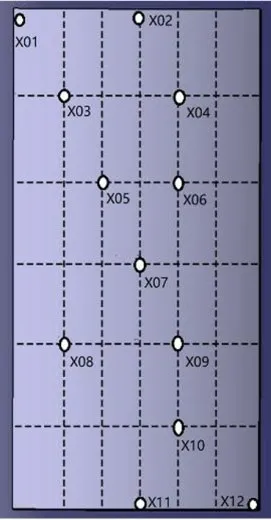
图7 型板表面热电偶布置位置Fig.7 Placement of thermocouples on the surface of the plate
2.2 结果对比分析
由于12 个热电偶采集的温度变化数据量大,为便于对比并同时考虑到流体流动方向等因素,因此选取斜对角线的5 个热电偶(X01,X05,X07,X09,X12)逐一进行仿真温度与实验温度的对比分析,如图8、图9所示。
从图8、图9 可知,实验数据与仿真数据趋势大体一致,由于对热压罐等的模型进行了简化,仿真时设定的热压罐端面边界条件和标准K-e 模型均与实际情况存在一定的差别,导致了误差。
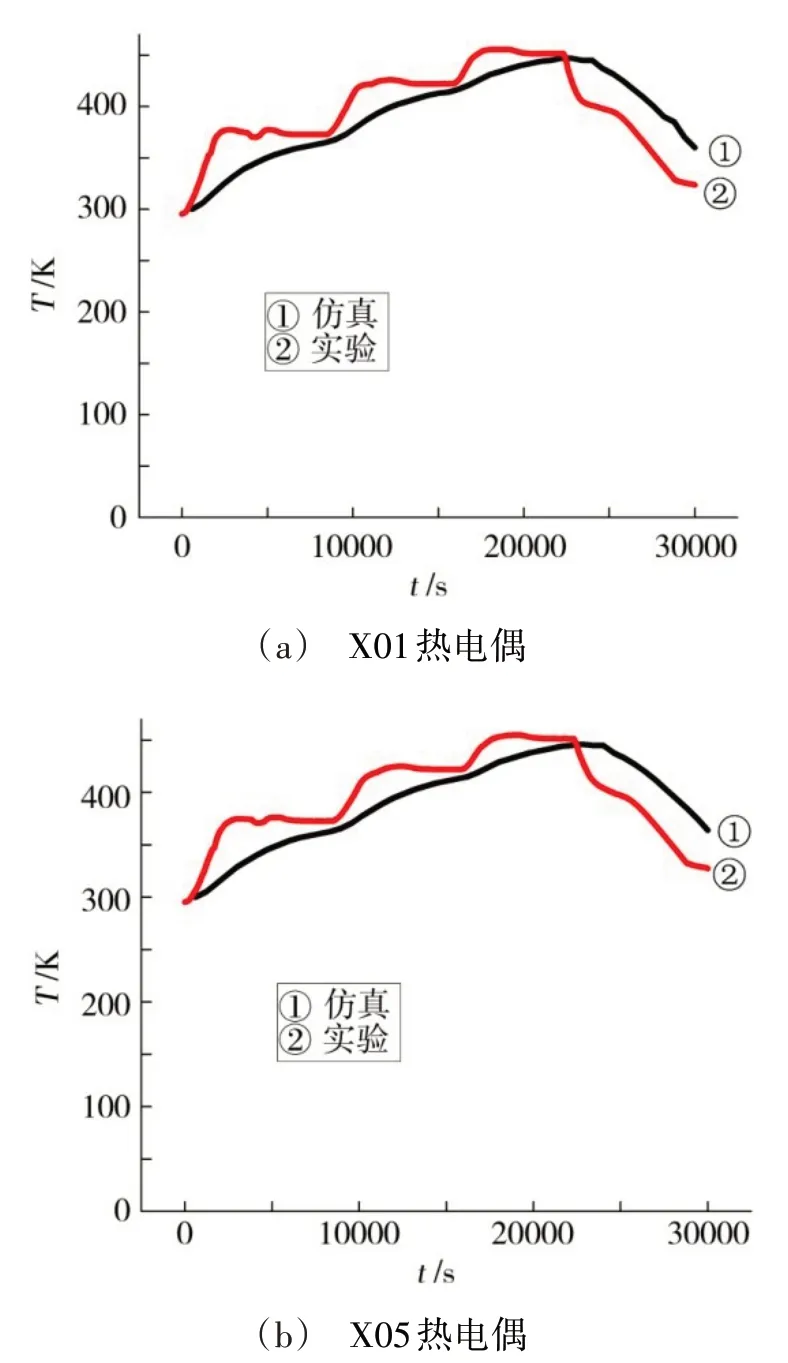
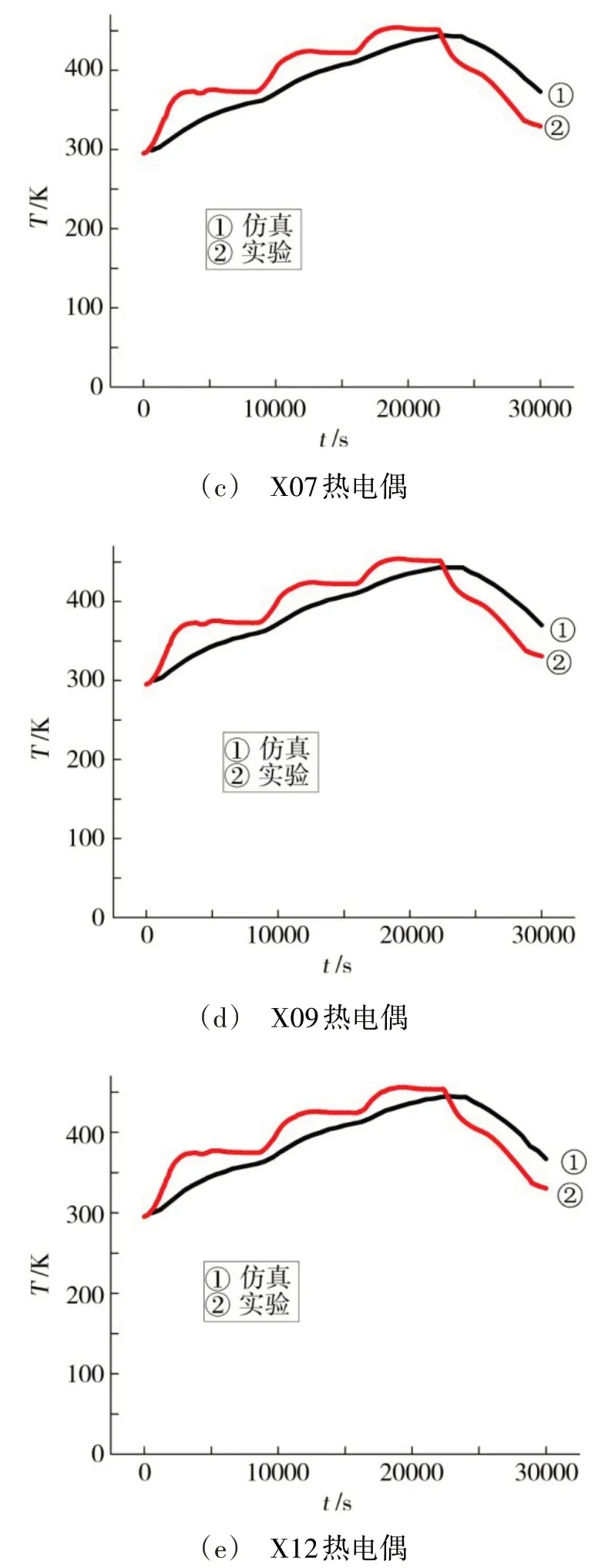
图8 仿真温度与实验温度的逐一对比Fig.8 Comparison of simulated temperature and experimental temperature data
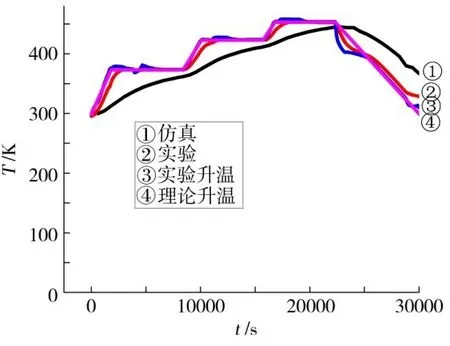
图9 仿真温度和实验温度的平均与升温对比Fig.9 Simulated temperature vs experimental temperature
5 个热电偶的实验平均温度与仿真平均温度的最大差值出现在2 400 s 左右,最大相对误差为12.3%,而平均相对误差为7.4%,在实际工程中是可接受的误差范围。因此,建立的热压罐成型工艺中框架式模具温度场的数值模型能够为真实构件的模具温度场分析提供参考。
3 模具支撑板厚度对模具温度场的影响
框架式模具的支撑结构具有U向和V向支撑板、通风孔和散热孔四个特征,其中U向与空气的流动方向垂直,V向与空气的流动方向平行。支撑板用来给型板提供支撑,防止变形,但支撑板的存在会阻碍热压罐中空气的流动,不利于型板下表面和空气的热对流,导致型板表面温度场的不均匀。
3.1 支撑板厚度对模具温度场分布的影响
为了研究支撑板厚度对于型板表面温度均匀性的影响,保持其余的模具设计参数和工艺参数不变,选取5组厚度,分别为4、6、8、10和12 mm。另外为节约时间,便于分析结果,在进行网格划分时对模具进行适当的简化:去除支撑板上的通风孔,并取前述固化工艺温度曲线中的前两个升温阶段和保温阶段作为固化工艺温度曲线。
大多数研究中对模具型板表面温度均匀性的判断参数均采用最大温差,但最大温差只能反映温度数据中两个极端值的大小情况,容易受个别特殊值的影响,而方差引入了更多的数据,能更好地反映数据的波动大小,方差越大,数据波动越大,因此本文选择温度方差作为判断参数。
在FLUENT 中完成温度场仿真后,利用CFDPOST 进行后处理,对型板表面上均匀选取的50 000个点的温度数据进行方差的计算。
通过对5组不同支撑板厚度的模具进行模拟,得到了如图10所示的不同支撑板厚度下的模具型板表面温度方差随时间的变化曲线,如图11 所示的不同支撑板厚度下的型板表面温度平均方差。
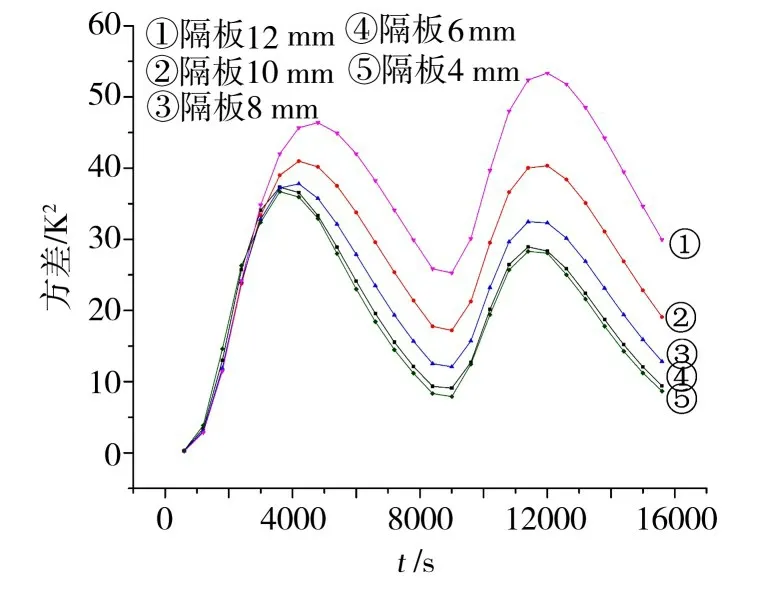
图10 不同支撑板厚度下的模具型板表面温度方差随时间的变化Fig.10 Variation of surface temperature variance of mold plate with time under different support plate thicknesses with time
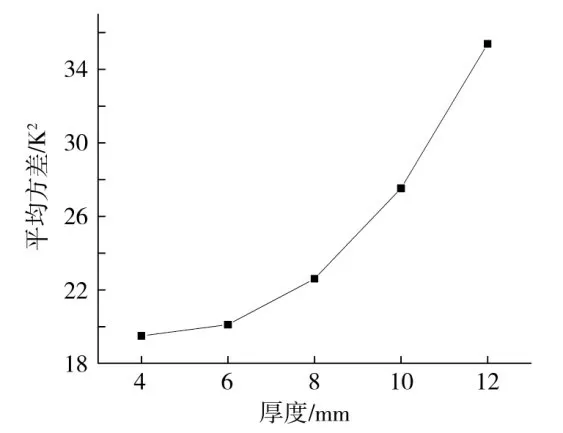
图11 不同支撑板厚度下的平均方差Fig.11 Average variance under different support plate thicknesses
从图10可知,在升温阶段,模具型板表面温度均匀性差,进入保温阶段后,温度方差的值逐渐降低,温度均匀性逐渐变好,随着下一个升温开始,温度方差值开始升高,均匀性降低。
由图10、图11 可见,随着支撑板厚度的增加,型板表面的方差逐渐增大,温度场的均匀性逐渐降低,因此设计框架式模具时,应在保证刚度的前提下,尽量减小支撑板的厚度,提高换热效率,增强型板表面的温度均匀性。
3.2 不同方向支撑板厚度的变化对改善温度均匀性的影响
两个不同方向支撑板的热交换方式不同,其中U向支撑板为射流冲击换热,V向支撑板为外掠平板换热。为了研究两个方向的支撑板厚度分别对型板表面温度均匀性的影响大小,设置两组对照实验进行研究,实验结果如表2和图12所示。
由图12可见U向支撑板厚度的变化对改善框架式模具型板表面温度场均匀性的影响比V向支撑板大。因此设计框架式模具时,应尽量减小支撑板的厚度,并且可以通过适当增大V向支撑板的厚度来保证模具的刚度要求。
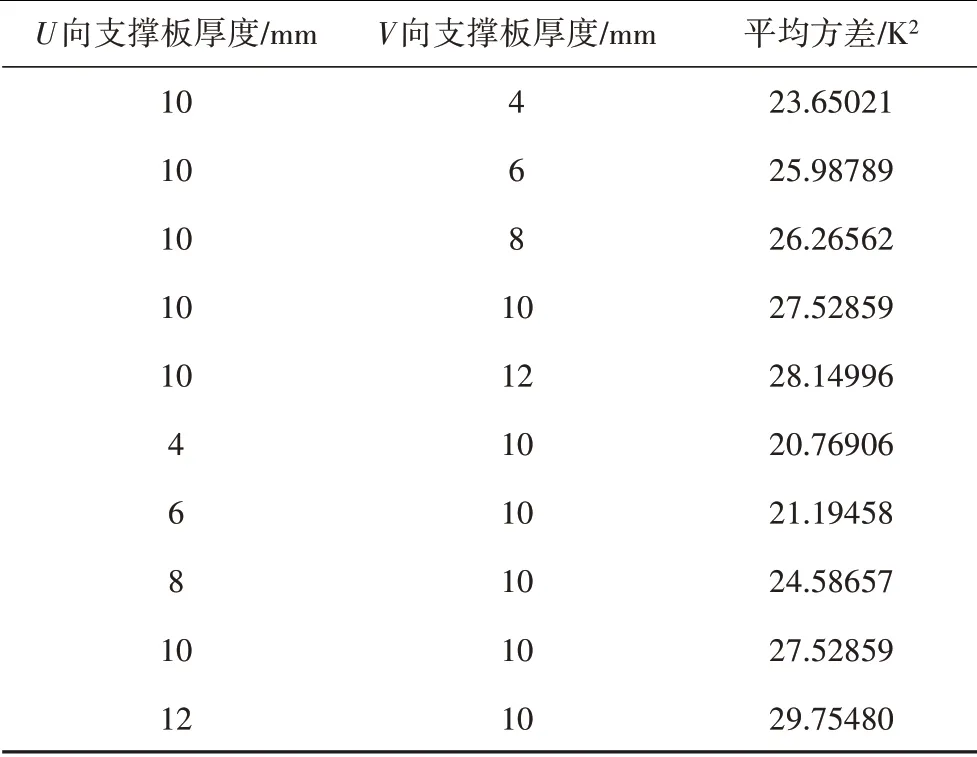
表2 设置的对照组Tab.2 Control group
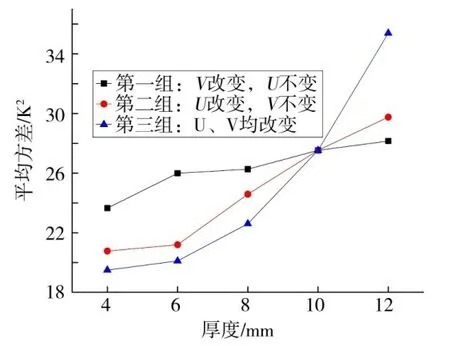
图12 不同方向支撑板厚度下的型板表面温度平均方差Fig.12 Mean square variance of surface temperature of the slab at different thicknesses of the support plate
4 结论
(1)以某型飞机蒙皮的热压罐固化为例建立了模具温度场的数值模型,将仿真数据与实验数据进行对比,平均相对误差为7.4%,在实际工程中是可接受的误差范围。因此建立的模具温度场仿真模型能够为真实构件的模具温度场分析提供参考。
(2)研究了支撑板厚度的变化和不同方向支撑板厚度的变化对于模具温度场分布的影响规律。结果表明,模具温度场的均匀性随着支撑板厚度的增加而逐渐降低,其中U向支撑板厚度的变化对温度场均匀性的影响比V向大。
