因子von Neumann代数上的非线性斜Jordan三重可导映射

宁 彤, 张建华

(陕西师范大学 数学与信息科学学院, 西安 710119)

0 引 言

设A是一个*-代数. 对A,B∈A, 称[A,B]*=AB-BA*为斜Lie积, 称A·B=AB+BA*为斜Jordan积. 近年来, 关于这两种积的研究得到广泛关注[1-10]. 设A和B是两个因子von Neumann代数,φ: A → B是一个双射(不必可加或线性), Li等[1]证明了对任意的A,B∈A, 有φ(A·B)=φ(A)·φ(B)当且仅当φ是一个*-环同构.

设φ: A → A是一个映射(不必可加或线性). 如果对任意的A,B∈A, 有φ(A·B)=φ(A)·B+A·φ(B), 则称φ是A上的非线性斜Jordan可导映射. 如果φ是可加的, 并且满足对任意的A∈A, 有φ(A*)=φ(A)*, 则称φ是可加*-导子. Zhang[2]证明了因子von Neumann代数上的每个非线性斜Jordan可导映射都是可加*-导子. 如果对任意的A,B,C∈A, 有

φ(A◇ξB◇ξC)=φ(A)◇ξB◇ξC+A◇ξφ(B)◇ξC+A◇ξB◇ξφ(C),

其中A◇ξB=AB+ξBA*, 则称φ是一个非线性ξ-Jordan三重*-导子. 显然, 当ξ=-1和ξ=1时,ξ-Jordan三重*-导子分别为*-Lie三重导子和*-Jordan三重导子. Li等[3]证明了在因子von Neumann代数上的每个非线性斜Lie三重导子都是可加*-导子. 本文考虑因子von Neumann代数上的非线性斜Jordan三重可导映射.

设H是一个复Hibert空间, B(H)是H上的所有有界线性算子全体, A⊆B(H)是一个von Neumann代数. 称A为一个因子是指其中心为I. 因子von Neumann代数A一定是素代数, 即A,B∈A且AAB=0蕴含A=0或B=0.

1 主要结果

定理1设A是复Hilbert空间上的因子von Neumann代数. 如果映射φ: A → A满足对任意的A,B,C∈A, 有

φ(A·B·C)=φ(A)·B·C+A·φ(B)·C+A·B·φ(C),

则φ是一个可加*-导子.

引理1[1]设A是一个因子von Neumann代数,A∈A. 如果对任意的B∈A, 有AB+BA*=0, 则A∈iI(i是虚数单位).

引理2[2]设A是一个因子von Neumann 代数,P∈A是一个非平凡投影且A∈A. 如果对任意的B∈PA(I-P), 有AB+BA*=0, 则存在μ∈, 使得

引理3设A是一个因子von Neumann代数,φ: A → A是一个非线性斜Jordan三重可导映射, 则下列结论成立：

1)φ(0)=0;

2)φ(iI)⊆iI;

3)φ(I)⊆I;

4) 存在α∈, 使得φ(P)*=φ(P)+αP.

证明: 1)φ(0)=φ(0·0·0)=φ(0)·0·0+0·φ(0)·0+0·0·φ(0)=0.

2) 设T∈A,λ∈, 由结论1), 有

0=φ(0)=φ(iλI·T·iλI)=φ(iλI)·T·iλI=iλφ(iλI)(T+T*)+iλ(T+T*)φ(iλI)*.

(1)

由式(1)可知, 对任意T∈A有φ(iλI)T+Tφ(iλI)*=0, 因此由引理1知, 对任意λ∈有φ(iλI)∈iI, 即φ(iI)⊆iI.

3) 设T∈A,λ∈, 由结论1), 有

由式(2)可知, 对任意T∈A有Tφ(λI)=φ(λI)T, 因此对任意的λ∈有φ(λI)∈I, 即φ(I)⊆I.

由式(3)可知,

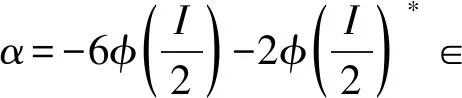
下面设A是一个因子von Neumann代数,φ: A → A是一个非线性斜Jordan三重可导映射,P1∈A为一个固定非平凡投影,P2=I-P1, Aij=PiAPj,i,j=1,2.

令U=P1φ(P1)P2-P2φ(P1)P1. 由引理3中4)可得U*=-U. 定义映射Δ: A→A为Δ(A)=φ(A)-[A,U]. 直接验证可知,Δ是一个非线性斜Jordan三重可导映射.

引理4φ是可加的.

断言1对任意的A12∈A12,B21∈A21, 有φ(A12+B21)=φ(A12)+φ(B21).

证明： 设T=φ(A12+B21)-φ(A12)-φ(B21). 由φ(0)=0及

(P2-P1)·I·A12=(P2-P1)·I·B21=0,

可得

另一方面, 有

于是

(P2-P1)·I·T=0.

(4)

对式(4)两边分别同乘P1,P2, 则P1TP1=P2TP2=0.

由A12·P1·I=0和φ(0)=0, 可得

另一方面, 有

Δ((A12+B21)·P1·I)=Δ(A12+B21)·P1·I+(A12+B21)·Δ(P1)·I+(A12+B21)·P1·Δ(I).

于是

T·P1·I=0.

(5)

对式(5)左乘P2、 右乘P1, 有P2TP1=0. 类似可证P1TP2=0. 所以φ(A12+B21)=φ(A12)+φ(B21).

断言2对任意的Aij∈Aij(i,j=1,2), 有:

1)φ(A11+A12+A21)=φ(A11)+φ(A12)+φ(A21);

2)φ(A12+A21+A22)=φ(A12)+φ(A21)+φ(A22).

证明： 设T=φ(A11+A12+A21)-φ(A11)-φ(A12)-φ(A21). 由P2·I·A11=0,φ(0)=0及断言1, 可得

另一方面, 有

于是

P2·I·T=0.

(6)

对式(6)左乘P1、 右乘P2, 左乘P2、 右乘P1, 左乘P2、 右乘P2, 则P1TP2=P2TP1=P2TP2=0.

由(P2-P1)·I·A12=(P2-P1)·I·A21=0 以及φ(0)=0, 可得

另一方面, 有

于是

(P2-P1)·I·T=0.

(7)

对式(7)两边左右同乘P1, 则P1TP1=0. 所以φ(A11+A12+A21)=φ(A11)+φ(A12)+φ(A21).

类似地, 可得2)也成立.

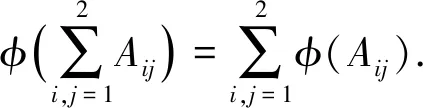
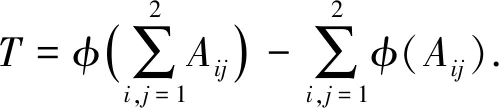
另一方面, 有

于是

P1·I·T=0.

(8)

对式(8)左乘P1、 右乘P1, 左乘P1、 右乘P2, 左乘P2、 右乘P1, 则P1TP1=P1TP2=P2TP1=0. 类似地, 可证P2TP2=0.

断言4对任意的Ajk,Bjk∈Ajk, 1≤j≠k≤2, 有φ(Ajk+Bjk)=φ(Ajk)+φ(Bjk).

另一方面, 有

结合式(9),(10)可知,φ(Ajk+Bjk)=φ(Ajk)+φ(Bjk).

断言5对任意的Ajj,Bjj∈Ajj(j=1,2), 有φ(Ajj+Bjj)=φ(Ajj)+φ(Bjj).

证明： 设T=φ(Ajj+Bjj)-φ(Ajj)-φ(Bjj). 由断言2中1),φ(0)=0以及Pk·I·Ajj=Pk·I·Bjj=0, 可得

另一方面, 有

于是

Pk·I·T=0.

(11)

对式(11)左乘Pj、 右乘Pk, 左乘Pk、 右乘Pj, 左乘Pk、 右乘Pk, 则PjTPk=PkTPj=PkTPk=0.

设Cjk∈Ajk(1≤j≠k≤2), 则由断言4, 有

另一方面, 有

于是Pj·T·Cjk=0. 从而由A的素性知PjTPj=0. 证毕.

由断言3～断言5, 对任意的A,B∈A, 有

即φ是可加的. 引理4成立.

引理5对任意的A12∈A12,A21∈A21, 有

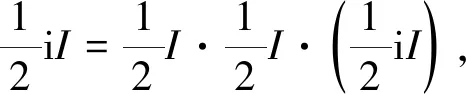
可得

因此α1=0, 从而

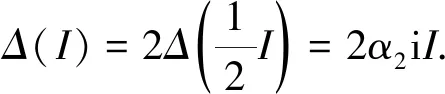
(12)

由式(12)以及2A12=I·P1·A12, 对任意的A12∈A12, 可得

因此有

Δ(A12)=Δ(P1)A12+A12Δ(P1)*+P1Δ(A12)+Δ(A12)P1.

(13)

对式(13)左乘P1、 右乘P2, 得

P1Δ(P1)A12+A12Δ(P1)*P2=0.

因而对任意的A12∈A12, 有

(P1Δ(P1)P1+P2Δ(P1)P2)A12+A12(P1Δ(P1)P1+P2Δ(P1)P2)*=0.

由引理2, 得

根据Δ的定义, 有

另一方面, 由0=P1·P2·I和引理3, 可得

P1Δ(P2)+Δ(P2)P1=0.

(14)

由式(13)可得Δ(A12)=P1Δ(A12)+Δ(A12)P1, 即有

Δ(A12)=P1Δ(A12)P2+P2Δ(A12)P1.

由式(14)可得P1Δ(P2)P1=P1Δ(P2)P2=P2Δ(P2)P1=0.

对任意的A21∈A21, 有

可得

Δ(A21)=Δ(P2)A21+A21Δ(P2)+P2Δ(A21)+Δ(A21)P2.

(15)

对式(15)左乘P2、 右乘P1, 对任意的A21∈A21, 得P2Δ(P2)A21=0. 因而P2Δ(P2)P2=0, 即Δ(P2)=0. 从而由式(15)可得

Δ(A21)=P2Δ(A21)+Δ(A21)P2.

于是,

Δ(A21)=P1Δ(A21)P2+P2Δ(A21)P1.

证毕.

引理6Δ(Aij)⊆Aij(i,j=1,2).

证明: 设Aii∈Aii. 由0=I·Pj·Aii(1≤i≠j≤2)和引理5, 可得

0=Δ(I·Pj·Aii)=2(PjΔ(Aii)+Δ(Aii)Pj),

从而

PiΔ(Aii)Pj=PjΔ(Aii)Pi=PjΔ(Aii)Pj=0.

因此Δ(Aii)⊆Aii.

设Aij∈Aij,Aji∈Aji(1≤i≠j≤2). 由Δ(AijAji)∈Aii和引理5, 可知

于是对任意的Aij∈Aij,Aji∈Aji, 有AjiΔ(Aij)*Pj=0. 从而由A的素性,PjΔ(Aij)Pi=0. 即Δ(Aij)⊆Aij. 证毕.

下面证明定理1. 由引理3, 存在λ∈使得Δ(iI)=iλI. 根据Δ的可加性, 有

4Δ(iP1)=Δ(I·P1·(iI))=I·P1·Δ(iI)=4iλP1.

于是Δ(iP1)=iλP1.

设A∈A使得S=P1AP2≠0, 由引理6,Δ(S)∈A12, 有

2Δ(iS)=Δ(I·(iP1)·S)=I·Δ(iP1)·S+I·(iP1)·Δ(S)=2iλS+2iΔ(S),

从而Δ(iS)=iλS+iΔ(S). 另一方面, 有

-2Δ(S)=Δ(I·(iP1)·(iS))=I·Δ(iP1)·(iS)+I·(iP1)·Δ(iS)=-4λS-2Δ(S),

从而4λS=0. 因此有λ=0, 即Δ(iI)=0.

设T=T*∈A, 则

4Δ(T)=Δ(T·I·I)=2Δ(T)+2Δ(T)*.

因此Δ(T)=Δ(T)*. 由

4Δ(iT)=Δ(I·T·(iI))=2iΔ(T)+2iΔ(T)*=4iΔ(T),

即Δ(iT)=iΔ(T).

设A=B+iC, 其中B=B*,C=C*, 则对任意的A∈A, 有

Δ(A*)=Δ(B-iC)=Δ(B)-Δ(iC)=Δ(B)-iΔ(C)=Δ(A)*.

对任意的A,B∈A, 可得

因此,

Δ(AB+BA*)=Δ(A)B+AΔ(B)+Δ(B)A*+BΔ(A)*.

(16)

另一方面, 对任意的A,B∈A, 根据式(16), 有

将式(16)与式(17)相加, 得

Δ(AB)=Δ(A)B+AΔ(B).

因此,Δ是可加的*-导子. 定理1证毕.

作为定理1的应用以及文献[11]的结果, 可得如下推论：

推论1设H是无限维的复Hilbert空间,φ: B(H) → B(H)是非线性斜Jordan三重可导映射, 则存在T∈B(H)且T+T*=0, 使得对任意的A∈B(H), 有φ(A)=[A,T].