网络入侵中的模糊区域判断算法

黄 熙 岱

(广东海洋大学 数学与计算机学院, 广东 湛江 524088)

网络入侵作为影响网络用户系统信息安全[1]的首要因素, 不仅可导致网络信息泄露, 甚至可导致网络用户严重的生命、 财产损失. 因此, 有效检测网络入侵行为, 准确、 高效地判断网络入侵中的模糊区域, 是网络入侵检测[2]领域内亟待解决的问题.

目前, 对网络入侵中的模糊区域判断算法的研究已有许多成果. 文献[3]提出了一种融合FAST(features from accelerated segment test)特征选择与自适应二进制量子引力搜索支持向量机的网络入侵判断算法, 该算法首先过滤掉原始特征集中的冗余特征, 得到候选特征子集, 再利用二进制量子引力搜索算法对候选特征子集与支持向量机(SVM)分类器参数进行优化, 通过量子位离散交叉操作摆脱种群进化停滞时的局部极值, 最后采用动态自适应调整策略平衡算法搜索能力, 但算法未考虑网络入侵中的模糊区域, 判断效率较差； 文献[4]提出了一种基于层次属性约减模型的网络入侵中模糊区域判断算法, 该模型采用双层进化思想, 结合粗糙集和遗传算法进行属性约减, 对数据进行预处理并分层划分形成决策规则集, 将层次评价知识库的进化数据传入种群空间, 在种群空间利用粗糙集和遗传算法进行进化和约减, 得到各层的优选属性集, 设计出层次分类器, 但未考虑算法的自适应及容错性, 具有判断效率和稳定性较差的缺点； 文献[5]提出了一种基于非平稳数据流下的网络入侵中的模糊区域判断算法, 利用蚁群算法选择网络入侵数据特征子集, 并消除其中冗余特征, 通过计算增益, 确定自己特征权重, 利用Bayes分类器对各特征权重进行分类, 计算出非平稳数据流下网络入侵中的模糊区域判断类别后验概率值, 最后利用辨别函数, 完成对非平稳数据流下网络入侵中模糊区域的判断, 但未考虑判断结果中的警报洪流现象, 忽视了其中的异常警报, 导致判断准确性较差.

针对上述问题, 本文提出一种基于多层逻辑结构的网络入侵中模糊区域判断算法. 首先采用基于多层逻辑结构的模糊区域判断算法, 进行输入、 量化输入、 迭代确认、 对量化输出结果反模糊化处理的操作; 再通过警报合成算法得到最优模糊区域判定结果, 以实现高效、 稳定地对网络入侵中模糊区域进行判断, 为网络信息安全发展提供一种新模式.

1 算法设计

高效检测网络入侵行为, 并准确判断网络入侵中的模糊区域, 是保证网络安全发展的前提. 而当前网络入侵中的模糊区域判定方法, 未考虑算法的自适应及容错性, 使判断效率较低, 且稳定性较差. 为解决上述问题, 本文提出一种网络入侵中的模糊区域判断算法, 基于多层逻辑结构, 进行精准的模糊区域判断, 最后通过警报合成算法将较多雷同警报合成为一条警报, 使警报洪流的规模下降, 最终得到最佳模糊区域判断结果. 本文算法流程如图1所示.

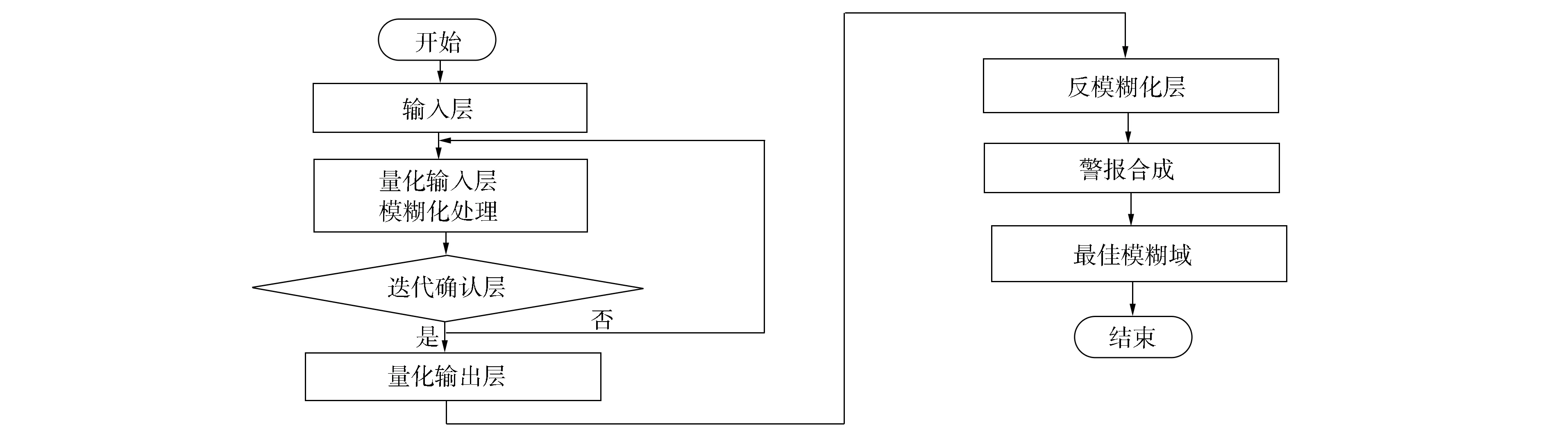
图1 算法流程

根据本文算法的基本流程, 进行具体的模糊区域判断操作, 再由警报合成获取最优的模糊区域判定结果, 以防止网络入侵行为的发生, 保证用户信息安全.

1.1 基于多层逻辑结构的模糊区域判断

针对网络入侵中的模糊区域, 其判断算法不仅要有较强的知识表述和模糊推理能力, 还应具有一定的自适应能力及并行容错处理[6]能力, 所以本文在判断网络入侵中的模糊区域时, 采用基于多层逻辑结构的模糊区域判断算法, 该算法基于自适应及容错性, 将模糊化层与信息输入层相结合, 充分发挥各自的优势, 互补不足, 实现准确、 高效地网络入侵模糊区域判断.

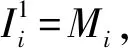
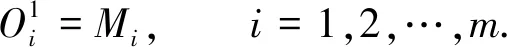
(1)

对算法第一层的输入判断结束后, 该层输出进入算法的第二层. 算法的第二层即量化输入层, 该层的主要作用是模糊化处理[7]待判断的网络入侵行为数据变量, 并确定其模糊化关联变量隶属度δk[8], 确定的依据是网络入侵检测数据与正常值的差. 用r表示不同输入网络变量包含的模糊区间个数, 则算法第二层中包含L=x×r个数据, 第二层内Mi的模糊项相对的判断单位序号可用k描述, 用xk表示x个判断单位的序号, 则该层的输入和输出分别为

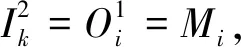
(2)

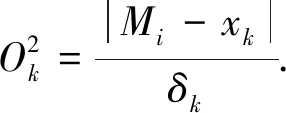
(3)

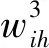
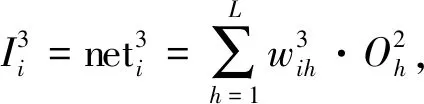
(4)

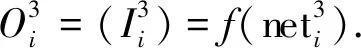
(5)

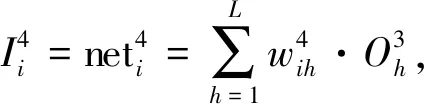
(6)

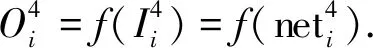
(7)

算法的第五层为反模糊化层, 该层的主要功能是反模糊化处理判断结论内的模糊变量集, 即模糊区域[11], 该层的输出为

(8)

其中m表示模糊化阈值. 在算法的迭代确认层和网络变量量化值的输出层中, 所使用的激励函数[12]均为S型函数

对整个算法进行训练即可准确判断出网络入侵中的模糊区域.

1.2 警报合成算法

根据多层逻辑结构的模糊区域判断算法输出层的警报情形可实现网络入侵模糊区域的有效判断, 但其在特定环境中有较高几率形成较多雷同的警报, 该情形被定义为警报洪流[13]. 通常警报洪流内的警报雷同, 在较短的时间域中形成大量雷同警报并无实际意义, 为使警报洪流的规模下降或防止其形成, 在上述获取的模糊区域判断结果基础上, 采用警报合成算法将较多雷同警报合成为一条警报, 得到最佳模糊区域判断结果.

用β={pa,ma,mc,ti,tw,ac}、T和A分别描述合成警报基、 合成警报基形成的集合及邻近时间域中孤立警报形成的孤立警报集[14], 其中,pa,ma,mc,ti,tw,ac分别为警报原型、 合成警报、 合成数量、 合成时间间隔窗口、 已等待时间和合成警报窗口值.

假设所有的β∈T, 当β.tw≥β.ti或β.mc≥β.ac时,β的合成工作被停止, 返回至β.ma； 当β.tw≥β.ti时, 去除T内的β； 当β.mc≥β.ac时, 对合成数窗口及合成时间窗口实施调整, 再次进行合成:

β.ac=β.ac×2,

(9)

β.ti=β.ti×2,

(10)

其中,β.ac和β.ti分别表示警报洪流规模和时间长度的预测值. 在β.mc≥β.ac的条件下, 警报洪流规模的预测值低于真实规模, 为使预测值与真实环境一致, 需调节预测值.

对新警报alert进行处理的过程为： 假设由β∈T导致ALERT_SIM(β.pa,alert)是真实的, 则alert能与β.pa实施合成; 反之, 如果含有警报p,p∈A, 导致ALERT_SIMB(p,alert)是真实的, 则需构建新的警报基[15]β′, 过程为

β′={p,alert,1,(alert.DetectTime-p.DetectTime)×(1+k),0,z},

(11)

其中k和z分别表示常系数和合成警报数初始值, 通常情形下k=0.1,z=2. 在T内添加β′, 假设alert不仅无法合成且无法构建新的合成警报基, 则将alert添加到A内, 在A内警报的数量超过10的条件下, 去除A内时间最久的警报, 并回到alert, 停止合成工作, 获取最佳模糊区域判断结果.

2 实验分析

2.1 实验环境数据集

实验为测试本文提出的网络入侵中模糊区域判断算法的性能优势, 将Window98, MATLAB7.0的语言编程环境作为实验测试平台, 分别采用本文算法和基于层次属性约减模型的网络入侵中模糊区域判断算法对UCI(https://archive.ics.uci.edu/ml/index.php), Kaggle(https://www.kaggle.com/datasets), AnalyticsVidhya(https://datahack.analyticsvidhya.com/contest/all/)和Quandl(https://www.quandl.com/)数据集实施网络入侵模糊区域判断. 实验数据集中各含有3 000条信息, 其中正常信息为2 400条, 网络入侵信息与模糊入侵信息共600条, 实验数据集信息列于表1.

表1 实验数据集的数据种类信息

2.2 检测率和误报率结果分析

在评判不同方法的判断性能时, 以检测率和误报率为评判标准, 其中误报率为错误警报数量与测试集内总信息数量的比值, 检测率为入侵行为的警报数量与入侵行为总量的比值. 本文算法(算法1)和基于层次属性约减模型的网络入侵中模糊区域判断算法(算法2)的判断结果分别如图2～图5所示.

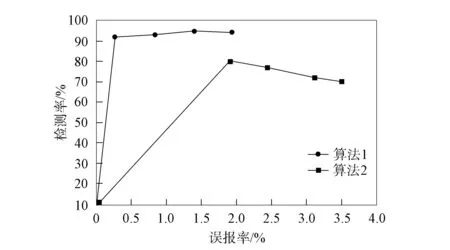
图2 两种算法对测试集1的判断结果

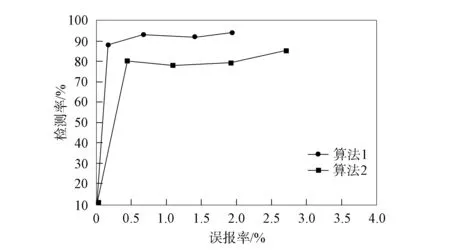
图3 两种算法对测试集2的判断结果

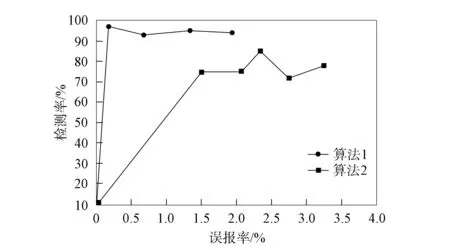
图4 两种算法对测试集3的判断结果

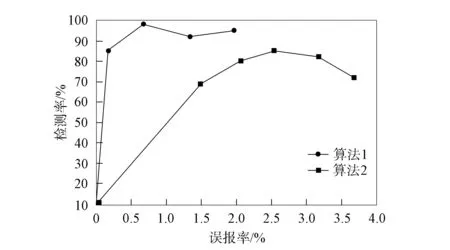
图5 两种算法对测试集4的判断结果

为了更清晰地体现对比不同测试集中不同算法的判断结果, 对图2～图5不同算法的判断结果进行汇总, 结果列于表2. 由图2～图5和表2可见: 在不同的测试集中, 基于层次属性约减模型的网络入侵中模糊区域判断算法的平均检测率变化范围为75.53%～80.03%, 平均误报率变化范围为1.66%～2.83%, 检测总体数据的检测率和误报率的平均值分别为78.33%和2.36%； 本文算法的平均检测率变化范围为91.74%～94.50%, 平均误报率变化范围为0.78%～1.13%, 检测总体数据的检测率和误报率的平均值分别为93.13%和0.97%. 实验结果表明, 使用本文算法判断网络中的模糊区域优越性显著[16].

表2 不同算法判断结果对比

2.3 运算时间结果分析

为验证本文算法在运算时间上的优势, 统计采用本文算法、 基于层次属性约减模型的网络入侵中模糊区域判断算法和基于非平稳数据流下的网络入侵中的模糊区域判断算法对上述实验中的4个测试集进行判断耗费的时间, 结果列于表3.

表3 不同算法的运算时间(s)对比

由表3可见: 使用本文算法判断测试集内网络入侵中的模糊区域时, 所需时间明显低于其他两种算法, 本文算法所需的最长时间为10.79 s, 最短时间为9.25 s, 平均时间为10.13 s； 基于层次属性约减模型的网络入侵中模糊区域判断算法所需的最长时间为16.59 s, 最短时间为11.89 s, 平均时间为14.14 s； 基于非平稳数据流下的网络入侵中模糊区域判断算法所需的最长时间为17.36 s, 最短时间为12.04 s, 平均时间为14.82 s. 实验结果表明, 使用本文算法判断网络入侵中的模糊区域时间优势明显[17].

2.4 内存占用率结果分析

为测试本文算法的内存占用率, 对比分析本文算法、 基于层次属性约减模型的网络入侵中模糊区域判断算法和基于非平稳数据流算法对不同大小测试集中的网络入侵模糊区域进行判断时的内存占用率, 结果列于表4. 由表4可见: 随着测试集大小的不断增加, 3种算法的内存占用率均有不同程度的提升, 当测试集大小为100 MB时, 本文算法的内存占用率为9.83%, 而基于层次属性约减模型的网络入侵中模糊区域判断算法和基于非平稳数据流下的网络入侵中模糊区域判断算法的内存占用率分别为14.59%和12.90%； 当测试集大小为2 100 MB时, 本文算法的内存占用率为10.37%, 而基于层次属性约减模型的网络入侵中模糊区域判断算法和基于非平稳数据流下的网络入侵中模糊区域判断算法的内存占用率分别为22.31%和24.51%, 因此, 本文算法的内存占用率明显低于其他两种算法. 实验结果表明, 使用本文算法判断网络入侵中的模糊区域时内存占用率较低[18].

表4 不同算法的内存占用率(%)对比

2.5 警报合成结果分析

为测试本文算法的警报合成效果, 将 24 h的时间视为一个单独的采样点, 分别采用本文算法和基于层次属性约减模型的网络入侵中模糊区域判断算法判断网络入侵中的模糊区域, 对比10个不重叠的采样点中不同算法的警报合成, 结果分别列于表5和表6.

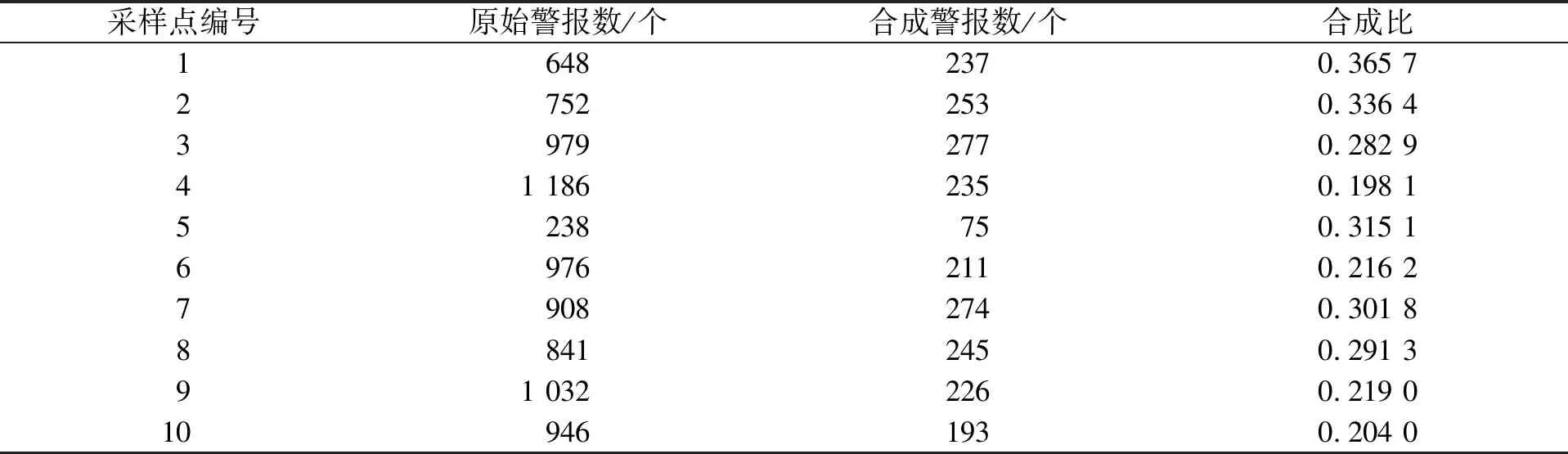
表5 本文算法的警报合成

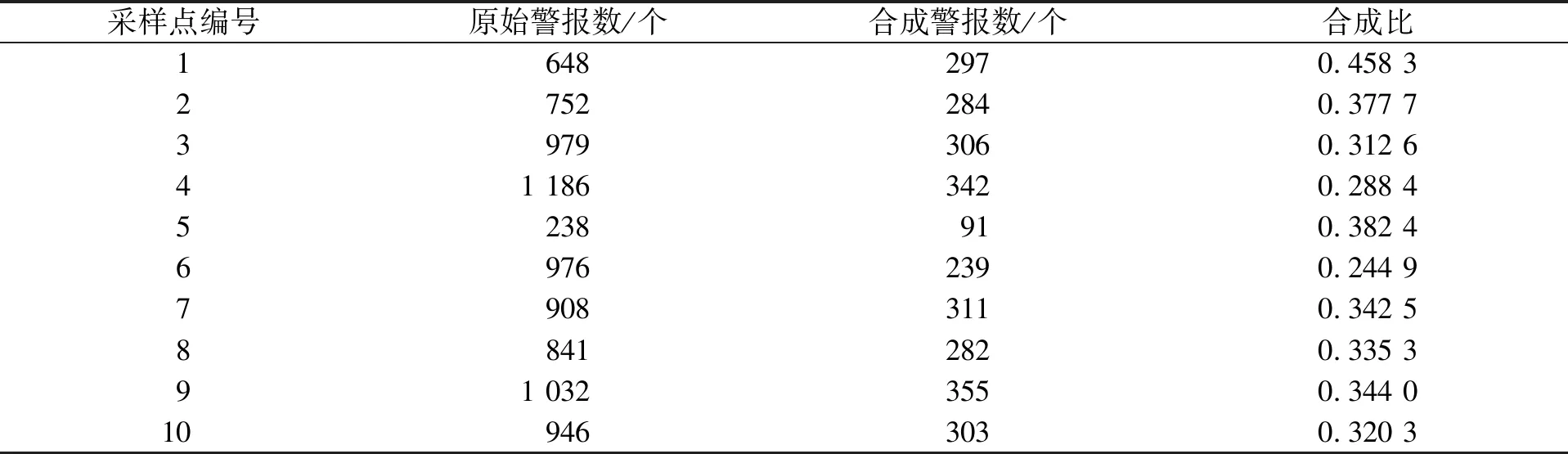
表6 基于层次属性约减模型的网络入侵中模糊区域判断算法的警报合成

由表5和表6可见: 在10个采样点中, 本文算法的警报合成比最高为0.365 7, 最低为0.198 1, 合成比总数为2.730 5； 基于层次属性约减模型的网络入侵中模糊区域判断算法的警报合成比最高为0.485 3, 最低为0.244 9, 合成比总数为3.406 4； 基于层次属性约减模型的网络入侵中模糊区域判断算法的合成比总数高于本文算法0.675 9. 因此, 在网络入侵中的模糊区域判断中本文算法的警报合成性能较好.

2.6 运行结果准确度结果分析

为验证本文算法的稳定性, 分别使用本文算法、 基于层次属性约减模型的网络入侵中模糊区域判断算法和基于非平稳数据流下的网络入侵中模糊区域判断算法进行100次网络入侵中模糊区域的判断实验, 对比不同算法的准确度, 结果列于表7.

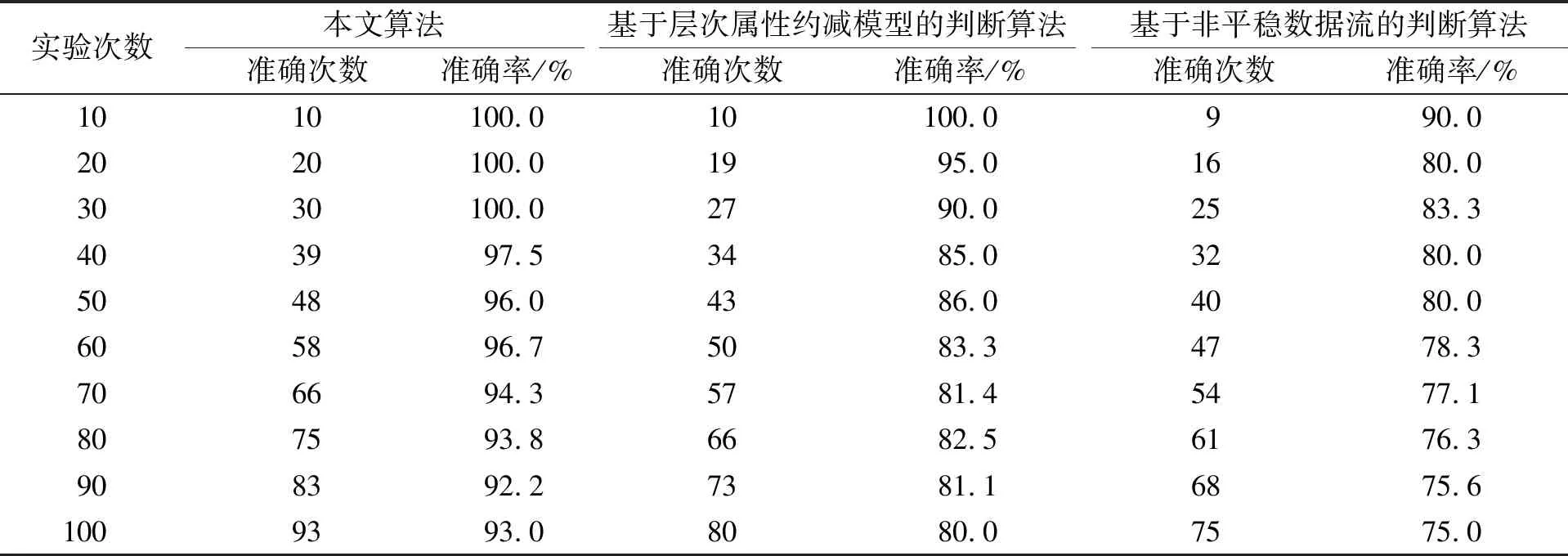
表7 不同算法的运行结果准确度对比

由表7可见, 采用3种不同算法判断网络入侵中模糊区域时, 当实验次数逐步增加, 3种算法的准确率都随之逐步降低. 但相比于其他两种算法, 本文算法的准确率下降较平缓. 当100次判断实验结束后, 本文算法的准确率仍保持在93%以上, 而基于层次属性约减模型的网络入侵中模糊区域判断算法和基于非平稳数据流下的网络入侵中模糊区域判断算法的准确率分别为80%和75%. 实验结果表明, 使用本文算法判断网络入侵中的模糊区域时稳定性较高.

综上所述, 本文提出了一种基于多层逻辑结构的网络入侵中模糊区域判断算法. 首先采用基于多层逻辑结构的模糊区域判断算法获取网络入侵中模糊区域的判断结果； 然后基于判断结果, 通过警报合成算法降低雷同警报数量, 防止警报洪流的形成或降低警报洪流的规模, 实现网络入侵中模糊区域的准确判断. 实验结果表明, 与基于层次属性约减模型的判断算法相比, 本文算法的检测率平均值上升14.8%, 误报率平均值降低1.39%, 对于网络入侵模糊区域的警报合成比总数降低0.675 9, 准确率保持在93%以上. 本文算法检测总体数据的检测率和误报率的平均值分别为93.13%和0.97%, 实验结果表明, 使用本文算法能准确地判断网络入侵中的模糊区域.