连续曲线梁桥在多车荷载作用下的动力响应

陈水生, 罗 浩, 桂水荣

(华东交通大学 土木建筑学院, 江西 南昌 330013)

近年来,曲线梁桥被广泛应用于高速公路的跨河互通、大跨桥梁的桥头引道和大型立体交叉中.相较于直线梁桥而言,曲线梁桥的曲率因素使曲线梁桥存在弯扭耦合效应,结构的受力分析变得更复杂.目前,国内外对曲线梁桥静力分析理论和计算方法的研究较多[1],使曲线梁桥的力学理论得到较好完善,但对公路曲线梁桥车桥耦合振动的研究较少.以往研究成果表明:车辆模型的选用对车桥耦合振动响应结果产生很大的影响[2].S. S.LAW等[3]采用7自由度的双轴三维车辆模型,将车辆荷载模拟成一列具有一定间距的活动荷载,分析了变截面梁结构在车辆荷载作用下的动力响应.HUANG D. Z.等[4-5]采用11自由度的车辆模型,通过有限元方法建立桥梁模型,研究了多片I型梁桥和曲线箱梁桥在多车荷载作用下的动力响应.M. R. AWALL等[6]通过ANSYS软件模拟三维车桥模型,研究了桥梁顶部横向支撑对I型曲线桥动力响应的影响,并认为曲率对自然频率、模态和竖向位移有重要影响.李忠献等[7]采用基于剪力柔性梁格法建立曲线箱梁的梁格模型和7自由度空间车辆模型,分析了桥梁冲击系数的影响因素.黄晓敏等[8]基于剪力柔性梁格理论,提出适用于曲线桥动力分析的三梁式桥梁模型,研究了多车荷载等因素对混凝土曲线梁桥的车桥耦合振动的影响.

已有的研究成果主要集中于单车荷载作用下的车-曲线梁桥耦合作用[9]和多车荷载作用下钢箱梁曲线梁桥[10]的冲击系数的研究,而对混凝土连续曲线薄壁箱梁桥的研究较少.笔者假定车辆荷载由一组固定间距的同种类型车辆组成,考虑阻尼比和桥面平整度的影响,研究混凝土连续曲线箱梁桥在多车荷载共同作用下挠度冲击系数的变化规律,为混凝土连续曲线梁桥的设计、养护、加固维修和今后的进一步研究提供参考.

1 车桥耦合振动分析模型

1.1 车辆模型

笔者以三轴自卸卡车作为研究对象,根据汽车的结构特性,将车辆模型简化为由车体、车轴、轮胎和弹簧式悬架支撑系统组成的体系.该车模型有16自由度,包括车体竖向和横向振动、纵向点头及侧翻振动,其中悬架支撑系统和轮胎均模拟为线弹性弹簧和阻尼器,且质量集中在车轴上,车身质量集中在车体重心上.三维车辆模型如图1所示.车辆动力特性参数参照文献[11].分析过程中,假定车辆沿着平行于桥轴线行驶,且车辆模型中每一个集中质量所受离心力均水平作用于各自的质心处.

根据D′Alembert原理,建立的车辆运动方程为

(1)

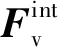
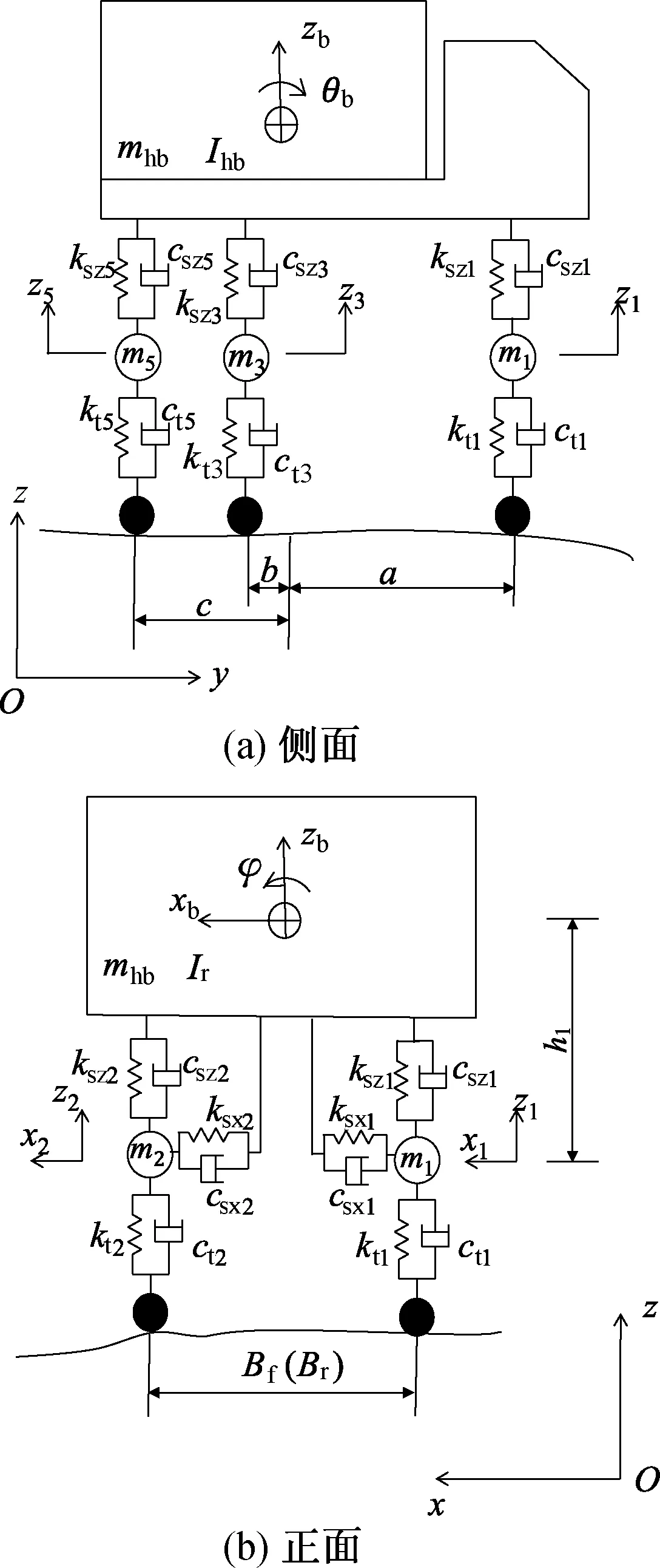
图1 车辆计算模型简图

1.2 桥梁模型

采用有限元方法分析,运动方程为

(2)

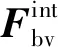
采用模态叠加法,通过广义坐标离散建模,取r阶模态,式(2)可以转换成模态方程,即

(3)

1.3 模拟桥面平整度

一般情况,将桥面平整度视为一个平稳的随机过程,可用功率谱密度函数来描述[12].通过傅里叶变换,根据此谱密度函数，采用三角级数叠加法，模拟得到桥面平整度函数.桥面平整度的样本表达公式为

(4)

式中:Aj为每段频率对应的平整度幅值;x为车辆行驶方向位移;nmid,j为每段空间频率的中值;θj为均匀分布在[0, 2π]上相互独立的随机变量;m为空间频率的划分段数.

1.4 车桥耦合模型

假定车辆在桥面行驶过程中,车轮与桥面始终保持接触不脱离,且考虑桥面平整度的影响,可得到第i个车轮与桥梁之间的相互作用力,即

(5)

(6)

(7)

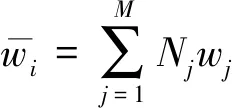
利用车轮与桥面接触点间的相互作用力与位移协调条件,联立式(1),(3)及(5),可得车桥耦合振动时变方程:

(8)

式中:M(t),C(t)和K(t)为广义矩阵,随车辆系统在桥上位置的移动而变化;F(x,t)为广义荷载列阵(包括离心力和超高分力);δ为桥梁模态广义坐标与车辆系统运动自由度组成的列阵,即δ=[q1q2…qrz1x1z2x2…z6x6zbxbθbφ]T.求解该时变系统方程时,笔者采用Runger-Kutta数值算法求解[13].

1.5 数值算法和程序设计

基于通用有限元软件ANSYS和MATLAB平台,先由ANSYS生成桥梁的有限元模型,得到桥梁各阶频率和相应的振动模态,然后采用Runge-Kutta数值算法,通过MATLAB语言编制相关程序,对式(8)进行求解,并综合考虑桥面平整度及其速度项.求解流程图如图2所示.

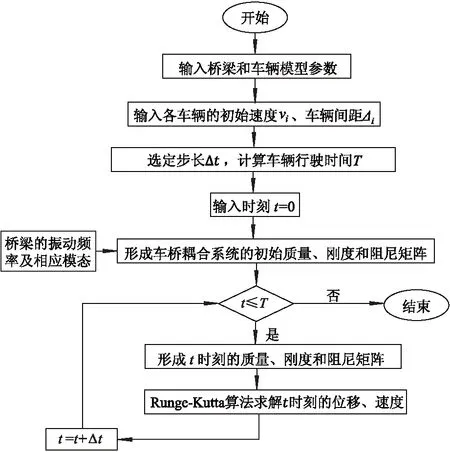
图2 车桥耦合振动响应求解流程图

2 实例分析

2.1 工程简介及建立桥梁模型

2.1.1工程概况

位于新余市长青南路立交A匝道的普通钢筋混凝土连续曲线箱梁桥[14],跨径为4×20 m.主梁为轴线半径53.0 m、宽8.0 m及高1.3 m的单箱单室曲形箱梁.顶板厚度为 22 cm,腹板厚度为45 cm,底板厚度为20 cm.

图3为主梁跨中截面示意图.桥面铺装为4 cm厚改进型中粒式沥青混凝土+6 cm厚改进型粗粒式沥青混凝土+3层FYT改进型防水层+8 cm 厚C40防水混凝土.

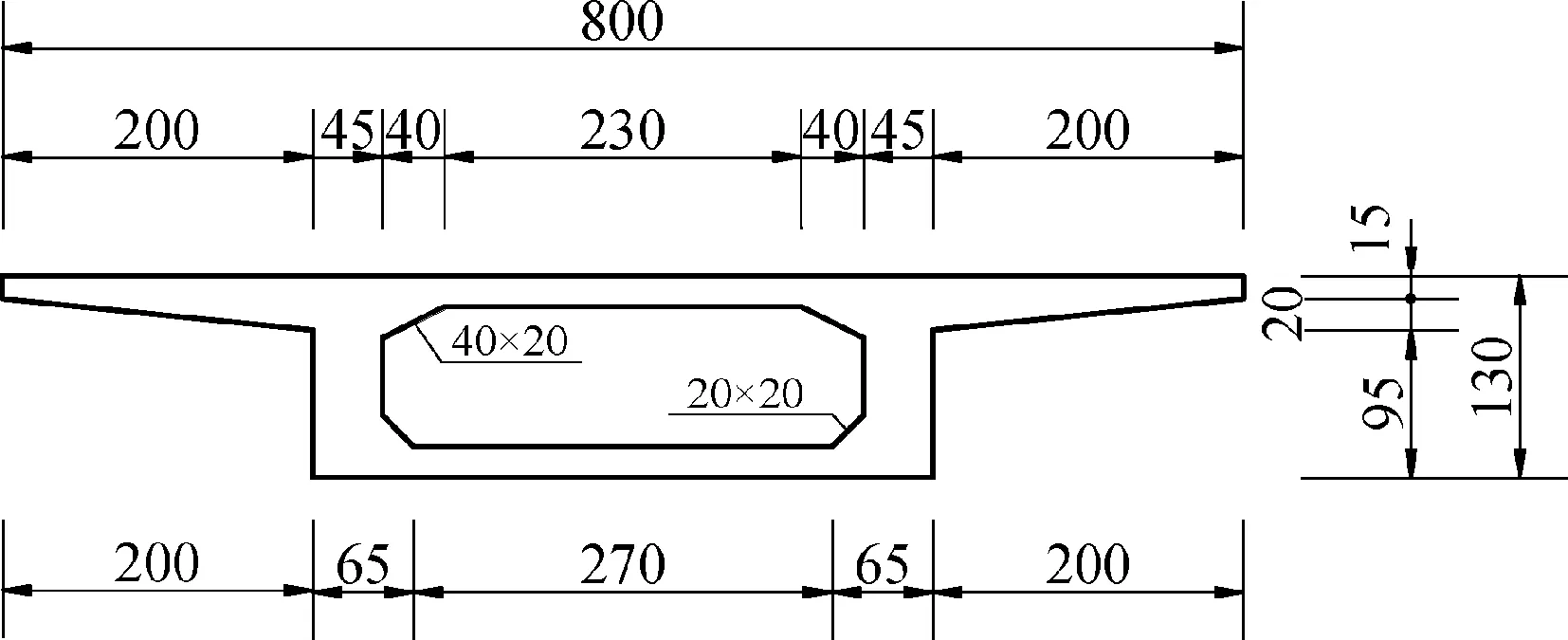
图3 主梁跨中截面示意图(单位:cm)

2.1.2建立有限元模型

对于曲线形箱梁桥而言,因梁截面主轴和作用荷载通常不在同一个平面内,所以其振动属于空间问题,需要选用空间单元对结构进行离散.为了较完整地考虑翘曲和扭转效应的影响,对桥面铺装采用shell43单元,对曲线梁采用solid45单元[6].对纵向每0.5 m为1个单元进行划分.根据主梁截面的变化,对截面横向进行灵活划分,根据截面等效刚度考虑截面钢筋,取主梁材料弹性模量为34.5 GPa,密度为2 600 kg·m-3,泊松比为0.167.对正中间墩采用三向固结,对内侧墩采用竖向和横向固定,对端部墩竖向固定和扭转进行约束.曲线梁桥有限元模型如图4所示.

图4 曲线梁桥有限元模型

2.2 曲线梁桥动力响应分析

2.2.1横向加载车辆数量的影响

为便于发现横向加载车辆数量对主梁动力响应的影响规律,对其他影响因素进行简化处理.车辆荷载靠外侧偏心行驶,车速为4～50 m·s-1,并以2 m·s-1递增.桥面平整度等级为A级,桥梁阻尼比为0.02.车辆的加载工况分别为单车道偏载(Case l)、横向双排车偏载 (Case 2)及横向双排对称 (Case 3),其中车辆偏载均为靠曲线外侧偏载,每排纵向车辆数量为1辆.横向加载车辆布置情况如图5所示,图中右侧为曲线外侧,左侧为曲线内侧.

图5 横向加载车辆布置情况

表1为横向加载车辆数量对跨中挠度最大冲击系数的影响.由表1中3种不同荷载工况下车桥耦合振动分析结果可知,随着横向加载车辆数量的变化,主梁的竖向挠度最大冲击系数变化较小.

表1 横向加载车辆数量对跨中 挠度最大冲击系数的影响

图6为横向加载车辆数量对跨中挠度冲击系数的影响.由图6可知:3种工况下,主梁跨中挠度冲击系数的变化规律基本一致,即随着横向加载车辆数量的变化,冲击系数变化很小,所受影响甚微;3种工况下,当车速为38 m·s-1时,主梁冲击系数均达到最大,且三者之间最大差值为3.77%.

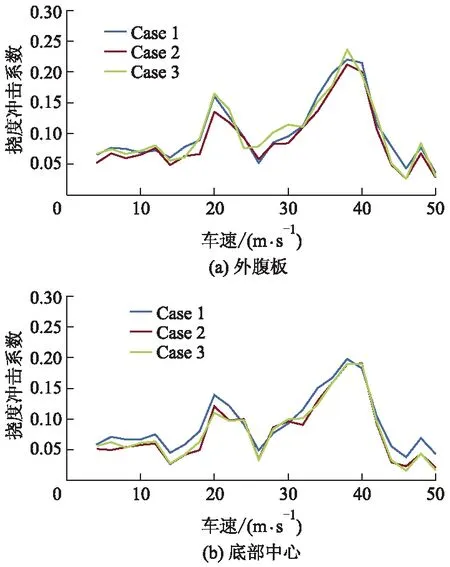
图6 横向加载车辆数量对跨中挠度冲击系数的影响

由图6还可知，随着车速增大,冲击系数呈无规则地波动变化.因此,设计过程中,应采用设计车速范围内的最大冲击系数来计算汽车荷载的效应.此外,当车速为4～50 m·s-1时,同一工况、相同车速下,跨中截面外腹板冲击系数大于底部中心,最大差值为17.8%,最小差值为2.70%.因此,选取冲击系数时,建议选用外腹板处冲击系数进行设计.

2.2.2纵向加载车辆数量的影响

选取横向布置为2.2.1节中的单车偏载 (Case1)工况,纵向车辆数量分别取1辆(VNl)、2辆(VN2)和3辆(VN3).车辆间距d=5 m.车速为4～50 m·s-1,并以2 m·s-1的速度递增.具体横向和纵向车辆荷载布置如图7,8所示.桥面状况为A级.桥梁仍选用2.1.1节所述桥型,车辆靠外侧偏心行驶,偏心距为2.1 m.

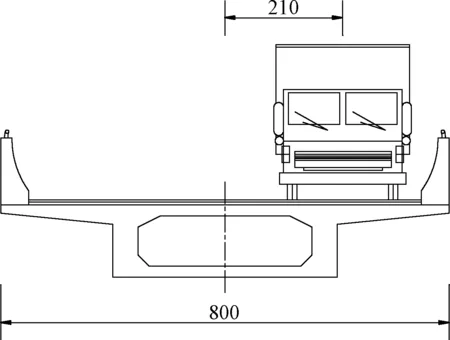
图7 横向车辆荷载布置示意图(单位:cm)

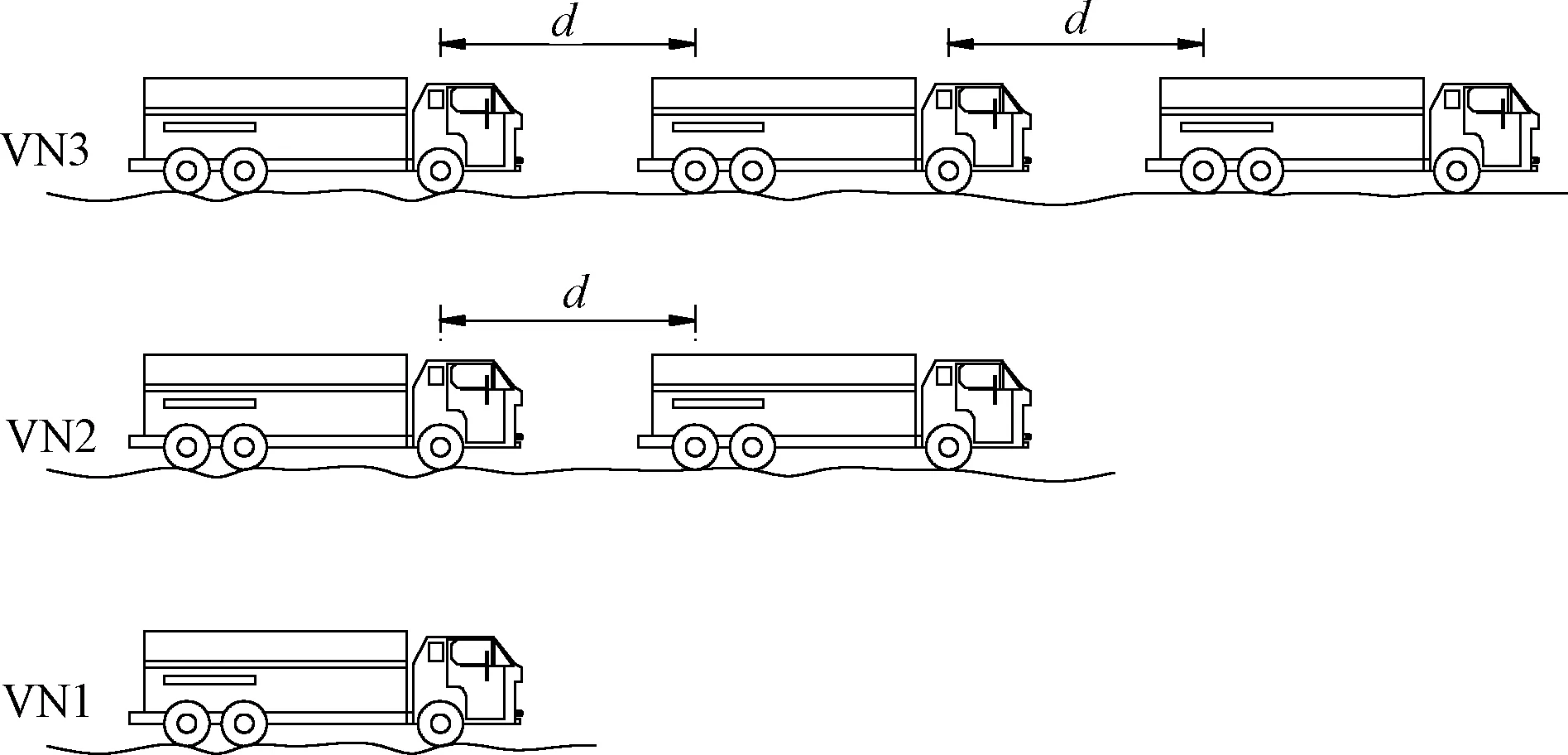
图8 纵向多车布置示意图

表2为纵向加载车辆数量对跨中挠度最大冲击系数的影响.由表2可知:纵向加载车辆数量对主梁的最大挠度冲击系数有很大影响,主梁跨中挠度最大冲击系数会随着加载车辆数量的增多而显著降低.同时,为便于分析纵向车辆数量的影响,以1辆车工况下的最大冲击系数为基准,对各工况进行对比分析.从而可知,纵向车辆数量为2辆和3辆时,外腹板处最大冲击系数分别降低至1辆车时的0.855倍和0.745倍,底部中心处分别降至1辆车时的0.919倍和0.874倍,这表明纵向车辆数量对主梁外腹板处最大冲击系数的影响更大.

表2 纵向加载车辆数量对跨中 挠度最大冲击系数的影响

图9为纵向加载车辆数量对跨中挠度冲击系数的影响.由图9可知:当车辆间距一定、车速为4～22 m·s-1时,冲击系数在单车工况下最大,且随加载车辆数量增多而显著减小,表明该因素对该桥冲击效应具有重要影响;当车辆间距一定、车速为24～50 m·s-1时,纵向车辆分别为2辆和3辆工况下,主梁冲击系数有围绕单车工况下冲击系数曲线上下波动的趋势;当车速为24～28 m·s-1和42～44 m·s-1时,2辆车作用下冲击系数最大;当车速为28～32 m·s-1和46～50 m·s-1时,3辆车作用下冲击系数最大;其他车速情况下,单车作用下冲击系数均为最大.此外,相同纵向车辆数量下的车速与冲击系数关系曲线基本相似,外腹板与底部中心处冲击系数的峰值车速也基本一致.

图9 纵向加载车辆数量对跨中挠度冲击系数的影响

2.2.3纵向车辆间距的影响

选取纵向为3辆车,根据文献[15],车辆间距d分别取为5,10,15和20 m.当车速为4～50 m·s-1时,对各间距下的最大冲击系数和最大挠度值进行比较.桥面状况为A级,桥梁模型和车辆偏心布置同第2.2.2节所述.

表3为车辆间距对跨中最大挠度冲击系数和最大挠度值的影响.由表3可知:随车辆间距增大,主梁跨中挠度最大冲击系数先增大后减小,而最大挠度值先减小后增大.可见,虽然冲击系数表面上是增大的,但将最大挠度和最大冲击系数结合起来看,实际上车辆间距小时的挠度较大些,表明冲击系数的增大趋势不会对结构的设计造成影响,因此该因素可以不考虑.

表3 车辆间距对跨中最大挠度冲击系数和最大挠度的影响

2.2.4桥面平整度的影响

为研究桥面平整度对梁桥动力响应的影响,车辆选取2.2.1节中单车偏载(Case 1)布置形式,车速为4～50 m·s-1,以2 m·s-1递增,匀速行驶在光滑、A级、B级和C级桥面上,分析桥面平整度对该梁桥挠度冲击系数的影响.单车荷载下不同路况的主梁跨中挠度冲击系数曲线如图10所示.由图10可知:冲击系数会随着桥面平整度等级的降低而显著增大,说明桥面平整度对单车荷载下主梁的冲击效应具有重要影响,因此在后期运营中应注意加强桥面的保养和维修.当车速为20 m·s-1时,冲击系数达到第1个峰值;当车速为36 m·s-1时,冲击系数达到第2个峰值;当车速达到44 m·s-1以上时,桥面平整度对主梁冲击系数的影响较小,主要因为车速较大时,系统所受离心力增大,导致主梁的竖向挠度受扭矩的影响大于桥面平整度.

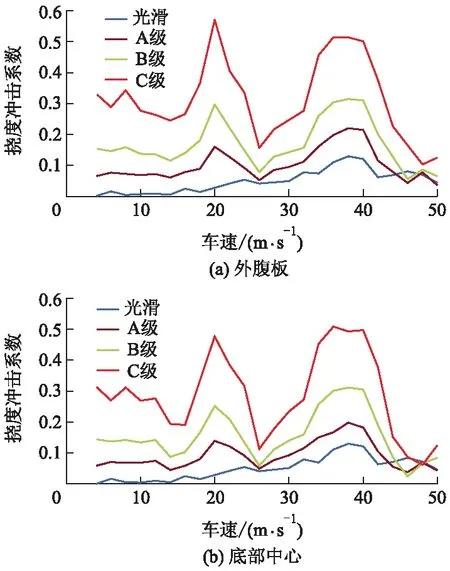
图10 不同路况下跨中挠度冲击系数与车速关系曲线

此外,为研究主梁在多车荷载作用下桥面平整度对该桥动力响应的影响,车辆选取2.2.1节中单车偏载、横向双排车偏载和横向双排车对称及2.2.2节中纵向两车、三车加载形式,以20 m·s-1的速度匀速行驶在桥面等级为光滑、A级、B级和C级桥面上,分析5种工况下桥面平整度对挠度冲击系数的影响.

图11为不同路况下跨中挠度冲击系数与路面等级关系曲线.由图11可知:桥面状况越差,冲击系数越大,说明桥面平整度对主梁在多车荷载作用时动力响应的影响同样显著.当车速为20 m·s-1时,单车工况下的冲击系数与横向双车工况下变化规律相同,数值相近,且均大于纵向两车、三车工况下冲击系数.此外,随桥面状况变差,前3种工况下冲击系数增长趋势大于后2种,即主梁在前3种工况下的动力响应对桥面平整度变化更敏感,这也说明在设计时,按单车荷载作用下冲击系数计算汽车荷载效应是较为安全的.

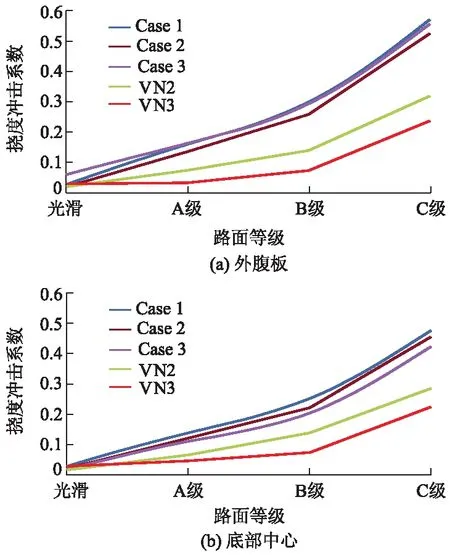
图11 不同路况跨中挠度冲击系数与路面等级关系曲线

3 结 论

1) 横向加载车辆数量对主梁挠度冲击系数的影响很小，对跨中截面外腹板动力响应的影响更大,建议取用外腹板处冲击系数进行设计.

2) 车速是冲击系数的重要影响因素之一,但冲击系数并不是随车速单调增加或减小,设计时,应采用设计车速范围内最大的冲击系数来计算汽车荷载的效应.

3) 纵向加载车辆数量对桥梁动力响应有很大影响.当车辆间距一定,车速在22 m·s-1以下时,桥梁挠度冲击系数在单车工况下最大,且随加载车辆数量增多而显著减小.此外,与底部中心处挠度最大冲击系数相比,纵向车辆数量对主梁外腹板的影响更大.

4) 虽然纵向车辆间距的变化对结构最大挠度冲击系数和最大挠度有一定影响,但将两者结合起来分析时,车辆间距小时的结构挠度更大,该因素对冲击系数的选取影响较小.

5) 随着桥面状况变差,主梁在单车和横向双车工况下的动力响应对桥面平整度变化较纵向两车、三车工况更为敏感.