基于不同湍流模型的挡板绕流数值模拟

王军锋, 许浩洁

(江苏大学 能源与动力工程学院, 江苏 镇江 212013)

挡板绕流[1]广泛存在于高炉炼铁[2]、流体换热、旋风除尘及湿法脱硫等工业领域,其流体流动状态发生改变的同时常伴有剪切、分离、回流等现象,其中涡旋的产生可在一定程度上强化化学反应、传热传质及多相混合,对过程强化有着重要影响.湍流作为一种以混沌性质变化为特征的流动,流动过程试验研究难度大且成本高,其流场中大小不同的非定常涡结构间的相互作用形成了极其复杂的流动状态,至今仍难以用确切的物理模型进行描述.

随着计算流体力学(CFD)技术的快速发展,数值模拟已逐渐发展成为低成本、高效率的湍流预测方法,工程应用广泛.常用的数值模拟方法主要有直接数值模拟(DNS)、大涡模拟(LES)及雷诺时均(RANS)方法等,其中湍流的非定常、多尺度等特性使得DNS的湍流计算代价巨大,且在有限的计算条件下,难以实现对工程中复杂湍流的预测,而在Navier-Stokes方程的求解中,湍流模型的引入可大幅降低计算量.LES的处理方式是对大尺度涡进行直接模拟,对小尺度涡采用湍流模型描述,计算难度得到一定改善.而RANS则完全通过模型求解,最大限度减少了计算量,已成为主要的工程数值计算方法.其基本思想是将Navier-Stokes方程对时间进行平均,从而将非定常湍流问题转化为定常问题.目前,湍流模型虽然种类多样,但仍然缺乏普适性模型.对于这一问题,许多学者[3-5]已对不同湍流模型在流化床、旋风分离器、轴流泵及离心泵等众多工业应用中的适用性进行了对比分析,得到了不同湍流模型的适用范围.由此可见,对于不同流动环境下湍流模型的合理选取是提高湍流预测准确性与可靠性的重要保障.

近年来,针对圆柱、方形等规则形状钝体绕流数值模拟中的湍流模型适用性问题,许多学者[6-8]进行了大量的研究.而对于挡板绕流,多集中于不同挡板结构参数下流体流动及对流换热的变化规律的研究[9-10],较少涉及不同湍流模型对流动过程预测结果的对比研究,尤其当绕流挡板为不规则异形结构时.因此,笔者基于所设计的抛光粉尘湿法除尘系统[11],选用4种典型雷诺时均(RANS)湍流模型:标准(Standard)κ-ε、重整规划群(RNG)κ-ε、剪切应力传输(SST)κ-ω以及雷诺应力(RSM)模型,对弓形绕流结构诱导产生的涡旋区域内的涡旋结构、压力分布及速度分布等关键参数进行数值模拟对比研究,并进行试验验证,进而分析不同湍流模型对于该绕流流动过程的适用性.

1 数学模型及控制方程

1.1 Standard κ-ε模型

Standardκ-ε模型广泛应用于各类工程流体计算中,其为半经验公式,且只适用于充分发展的湍流,主要通过求解湍动能κ方程和湍流耗散率ε方程来封闭N-S方程组求解流场,其方程如下:

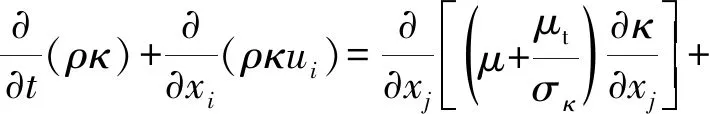
(1)

(2)

式中:ρ为流体密度;ui为流体平均速度;μ为流体黏度系数;σκ,σε分别为κ,ε的湍流普朗特数;Gκ为由于平均速度梯度而产生的湍流动能;Gb为由于浮力而产生的湍流动能;YM为可压缩流中脉动膨胀引起的总耗散率的变化;C1ε=1.44;C2ε=1.92;μt为湍流动力黏性系数,其表达式为

(3)

式中:Cμ=0.09.

1.2 RNG κ-ε模型

为提高计算模型适应性,V. YAKHOT等[12]于1986年在Standardκ-ε模型的基础上提出RNGκ-ε模型,该模型考虑了涡流对湍流的影响,提高了对旋流流动的预测精度.同时RNG理论还为该模型中湍流Prandtl数提供了解析公式,而非经验常数.其湍动能κ及耗散率ε方程如下:

(4)

(5)

式中:ακ,αε分别为κ,ε的有效普朗特数的倒数;μeff为有效黏性系数,μeff=μ+μt;Rε为新增项,以适应应变率和流线曲率变化的迅速流动.

与Standardκ-ε模型最大的区别在于耗散方程中的新增项Rε,使得RNG模型对快速应变和流线曲率的响应更加敏感.Rε的表达式为

(6)

式中:η为量纲一的应变或平均流时间尺度与湍流时间尺度之比;η0为η在剪切流中的典型值,η0=4.38;β=0.012.

式(5)可进一步改写为

(7)

式中:

(8)

式(7)-(8)中常数项C1ε,C2ε与Cμ由RNG理论给出,其值分别为C1ε=1.42,C2ε=1.68和Cμ=0.084 5.

1.3 SST κ-ω模型

在κ-ω模型中,ω被定义为特定耗散率,其中由F. R. MENTER[13]提出的SSTκ-ω模型描述了湍流黏度定义中的湍流剪切应力的传递,并结合使用了κ-ε和κ-ω,即对近壁区采用Standardκ-ε而对充分发展的远壁区域选用Standardκ-ω,从而提高了其在广泛自由流中的精确度和可靠性,尤其是在近壁区绕流和旋流方面.其湍动能κ及耗散率ω的方程如下:

(9)

(10)

式中:Γκ和Γω分别为κ和ω的有效扩散率;Yκ和Yω分别为κ和ω因湍流引起的耗散;Gκ,Gω分别为κ,ω引起的湍流动能;Dω为交叉扩散率.

(11)

(12)

式中:μt1为修正后的湍流黏性系数,其表达式为

(13)

式中:α*为抑制湍流黏度系数;S为应变率幅度;F2为湍流普朗特数的融合项；α1为常数.

1.4 RSM模型

RSM模型是一种精细的RANS 湍流模型,摒弃了各向同性的涡黏性假设,通过附加雷诺应力输运方程和耗散率方程来封闭N-S方程.典型的线性Pressure-Strain模型的控制方程如下:

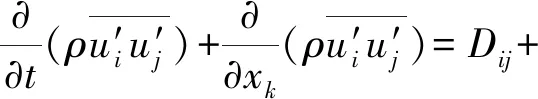
(14)

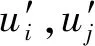
(15)

(16)

(17)

(18)

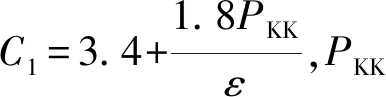
2 物理模型及网格划分

2.1 物理模型

选取设计的带有挡板结构的湿法除尘系统建立物理模型,该新型湿法除尘系统的结构示意图如图1所示.

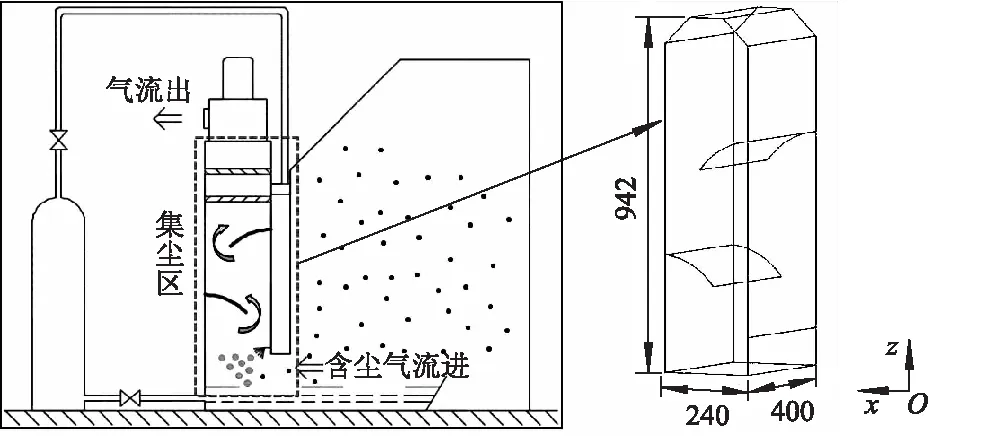
图1 除尘系统结构示意图(单位:mm)

系统运行时,含尘气流在风送流场作用下从底侧边进入集尘区,向上依次流经两块交替设置的弓形挡板,进而在装置内产生复杂的湍流流动.为了对比不同模型对该气相湍流预测的差异性,选取带有挡板结构的集尘区作为计算区域.由于集尘区沿图示y方向具有延伸性,即垂直于y方向的不同截面具有相同的截面形状,计算中发现其三维数值计算结果中不同y值处截面的流动参数差异性较小,且与二维数值模拟结果吻合较好.因此为了提高计算效率,选择集尘区在Oxz平面投影的二维结构进行不同湍流模型的数值模拟.

数值模拟过程中,流体定义为不可压缩空气,选用稳态SIMPLE算法,设置入口为速度入口边界,出口边界选用压力出口以减少回流的产生,设定来流湍流强度为5%,水力直径为0.1 m.壁面及弓形挡板板设置为无滑移固壁,且所有湍流模型近壁区均采用标准壁面函数进行修正.

2.2 网格划分

计算区域结构化网格划分如图2所示,其中集尘区总高H=942 mm,宽D=240 mm,进、出口宽度L1=L2=100 mm,安放角(即弓形挡板弦与所在壁面夹角)θ=60°,挡板弦长L3=165 mm,半径R=200 mm.图中选取的特征位置1与位置2对应的纵坐标分别为y=0.40 m及y=0.75 m.利用ICEM对该二维计算区域进行结构化四边形网格的划分,后在Fluent中进行数值计算.为提升计算精度,对壁面及挡板板附近区域进行了局部加密,全局网格质量Quality指标在0.93以上.选取位置1处的速度值分别对4种模型进行网格无关性验证,如图3所示.

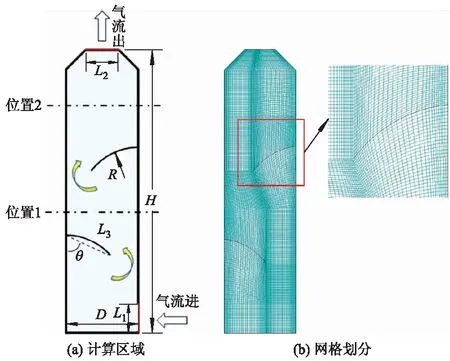
图2 计算区域结构化网格划分

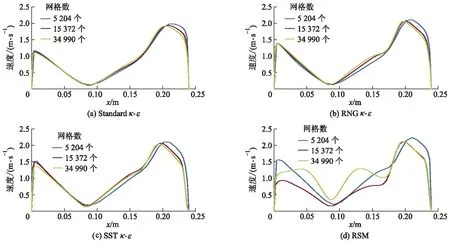
图3 网格无关性验证

从图3a-c可以看出:Standardκ-ε，RNGκ-ε及SSTκ-ω3种模型下速度值变化趋势相同,且随着网格数增加达到15 372个后,进一步增加网格数,速度变化增量均小于5%.从图3d可以看出:RSM模型对网格疏密表现较为敏感,具体表现为随着网格数量的不断改变,速度值变化明显,当网格数量增加至34 990 个时,速度波动最为剧烈,且出现多个速度极值.综合考虑计算精度与计算速率,确定计算网格数为15 372 个.

3 试验装置及方法

3.1 试验方案

为了获得集尘区内的真实流动特征以验证不同湍流模型预测结果的差异性,搭建了试验装置,如图4所示.试验装置主要包括连续激光、相机、风机及烟雾发生器.所选高浓度烟雾粒径为1～2 μm,对气相流场跟随性较好，且具有良好的反光性,故可近似通过烟雾流线表征气相流场流线.集尘区模型由透明亚克力板制成,并设定烟雾从风机入口给入,通过相机捕捉获得由连续激光所照亮的片光平面内的烟气流动情况.

选用微型手持转轮风速仪(见图5)对待测中心平面上的纵、横向速度分量进行测量.当转轮平面与x方向垂直时所测速度值为横向速度;当转轮平面与竖直方向垂直时所测即为纵向速度分量.

图4 试验装置图

图5 手持转轮风速仪

3.2 误差分析

涉及的测量值主要包括可视化涡旋结构及待测平面涡旋内的纵、横向速度分量.为了获得更接近于真实值的最佳测量结果,首先对比拍摄不同y值处截面的烟雾流动情况,发现其具有相似的流动特性,综合考虑烟雾反光效果及避免近壁区效应,最终确定连续激光拍摄平面为靠近相机一侧y方向长度的1/3处.

为保证测量的统一性,选择对连续激光照射平面进行涡内速度测量,由于转轮风速仪本身为侵入式测量仪器,对流场存在一定的干扰,系统误差难以避免.为了减少测量的偶然误差,通过对相同条件下的多次测量值取算数平均值.

4 模拟结果及分析

4.1 涡旋结构对比

4种湍流模型预测的气相流线及试验结果如图6所示.

图6 不同湍流模型预测的气相流线及试验结果

从图6可以看出:4种模型均能较好地预测集尘区内的气相流动特征,即从底部进入的气流,在挡板板后方诱导产生了2个尺度较大的涡旋,并根据涡旋产生位置，初步将其分为上部涡旋和下部涡旋,同时还可发现，在入口上方区域及挡板下方附壁区形成了多个小尺度涡.在第2块挡板与出口间区域的涡旋结构预测中,4种湍流模型表现出一定的差异性.Standardκ-ε,RNGκ-ε模型下,涡旋发展充分,整体性较好,且作用范围较大,较好地充满装置内部;SSTκ-ω则与RSM表现出一致性,涡旋数量增加,主要表现为在靠近第2块挡板区域出现了与主涡旋度方向相反的附壁涡.试验过程中拍摄获得的烟雾流动情况如图6e所示,与模拟结果对比发现,Standardκ-ε,RNGκ-ε模型对涡旋结构预测结果较其他2种模型与试验值更为接近.

4.2 压力分布对比

增设挡板后,装置内气相流动状态发生改变的同时,压力分布也出现明显变化.4种模型对不同入口风速工况下进出口压降的预测结果如图7所示.

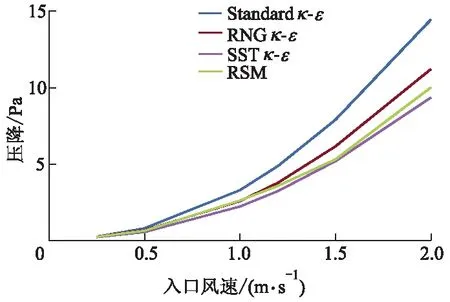
图7 不同模型对应的进出口压降情况

从图7可以看出:进出口压降均随着入口风速的增大不断增加,其中Standardκ-ε的压降明显大于其他3种模型,在入口风速为2.0 m·s-1时,其与SSTκ-ω预测结果偏差高达34.6%.在设备实际较优工况下(即入口风速为1.0～1.5 m·s-1),RNGκ-ε,RSM及SSTκ-ω3种湍流模型的预测结果较为接近;当入口风速为1.0 m·s-1时,RNGκ-ε与RSM模型的模拟数值仅相差1.5%;当入口风速为1.5 m·s-1时,SSTκ-ω与RSM模型的压降预测值偏差也只有2.3%.4种模型对于进出口压降的预测值由大到小顺序为Standardκ-ε,RNGκ-ε, RSM, SSTκ-ω.

为进一步分析不同模型对挡板附近压力分布预测的差异性,对比了位置1处的总压变化,对比结果如图8所示.

图8 位置1处的总压变化曲线

从图8可以看出:4种模型的预测结果均表现出相同的变化趋势,即在涡旋中心和快速流道区域分别出现压力极小值和极大值,在该区域内,流体流经挡板时,由于流道迅速收缩变窄,流体被挤压,在装置右侧(x约为0.20 m)产生向上运动的快速流道,流体总压升高,且在同一水平面达到极大值;流经挡板后,流道迅速扩张,挡板附近流体的动能消耗使得近壁区流体产生停滞及倒流,而快速流道区域流体仍继续向前流动,从而在挡板后方形成了流体的旋转运动,亦即涡旋;涡旋内部不断的有机械能向摩擦热的转换,进而使得涡旋区的压力下降,形成压力回流区,且在涡旋中心位置(x约为0.09 m)处出现压力的极小值.不同模型的预测差异则主要表现为极小值,从大到小的顺序为Standardκ-ε, RSM, RNGκ-ε, SSTκ-ω.而Standardκ-ε模型预测所得极大值产生位置相较于其他3种模型,则更靠近壁面.

4.3 速度分布对比

速度分布是表征涡旋特性的重要参数,位置1和位置2处不同湍流模型下的纵向速度对比曲线如图9所示,试验值为通过风速仪对实物模型进行测定获得.涡旋纵向速度模拟和试验值分布整体呈现由外圈向中心呈逐渐递减趋势,位置1和位置2分别对应2个不同的涡旋结构.对比两涡快速流道区域速度分布情况可以发现:下涡的快速流道宽度值较大,且纵向速度极大值较小;上涡快速流道较窄,由于流量一定,从而导致其速度极值高于下涡.

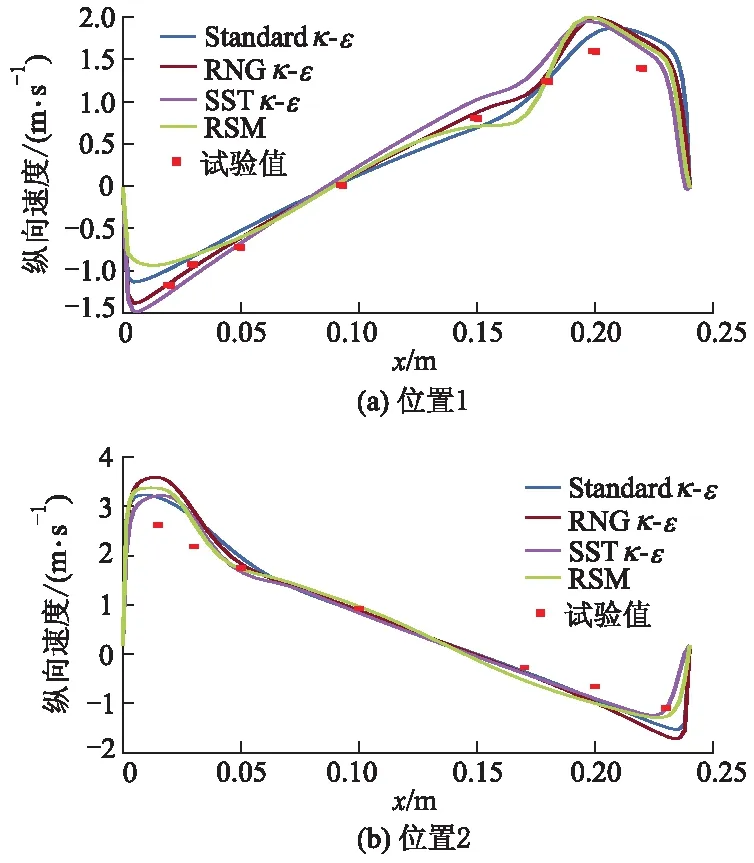
图9 不同位置处纵向速度的变化曲线

从图9a可以看出:纵向速度为0 m·s-1时,不同模型的预测值与试验值均吻合较好,在x=0.9 m附近,在快速流道区域,RNGκ-ε，SSTκ-ω及RSM 3种模型预测结果较为接近,且其速度极值位置点与试验的一致,Standardκ-ε模型模拟的极值位置点则更偏向壁面,与实际情况略有误差;在下涡的纵向速度预测中,RNGκ-ε的预测值与试验值整体吻合较好,在快速流道区域,数值模拟数值均大于试验值,可初步归结于选取壁面函数近似计算及近壁区网格密度不够.从图9b可以看出:在两侧近壁区,试验值与SSTκ-ω预测结果最为接近,初步判断原因为与κ-ε模型在近壁区采用标准壁面函数不同,κ-ω模型则是依赖于网格参数y+;在涡旋内部,4种模型预测结果均吻合较好.

横向速度主要受涡旋结构影响,下涡在第1块挡板的剪切和第2块挡板的导流作用下,涡旋沿顺时针方向产生了一定程度的倾斜,从而在位置1处产生了横向速度分量.位置1处不同湍流模型对横向速度的预测结果如图10所示.由于位置1 在涡旋中心偏上方,所以其横向速度大部分为沿x负方向,其绝对值大小呈先增加后减小的趋势.对比不同模型的模拟结果,可以发现SSTκ-ω模型预测值与试验值吻合较好.

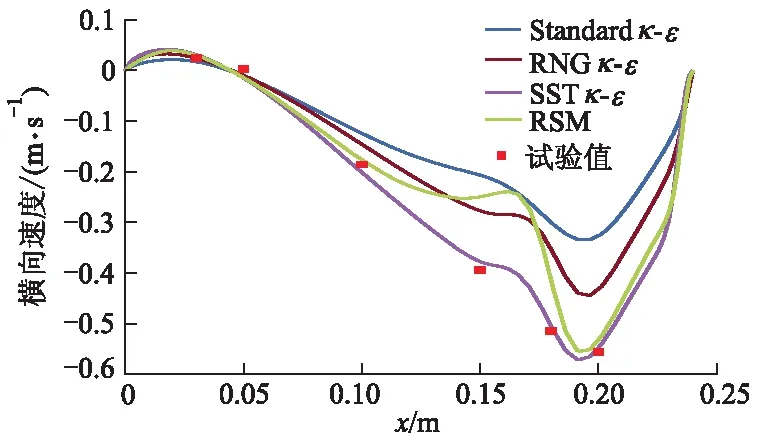
图10 位置1处横向速度变化曲线

5 结 论

1) RSM模型计算结果受网格密度影响较大,对网格精度要求高,计算量大,难以广泛应用于工程计算中.

2) Standardκ-ε和RNGκ-ε模型较SSTκ-ω和RSM模型更准确地预测了挡板诱导产生的涡旋结构.对于进出口压降数值模拟,4种湍流模型的预测值从大到小顺序为Standardκ-ε, RNGκ-ε,RSM, SSTκ-ω,其中Standardκ-ε的预测值与其他3种模型的预测值偏差较大,最大偏差值高达34.6%;且基于Standardκ-ε模型的模拟结果中,极大值产生位置较其他3种模型更靠近壁面.

3) 在涡内速度分布预测中,其纵向速度的RNGκ-ε模型的预测结果与试验值吻合较好;在涡旋外圈(即近壁区),不同模型的数值模拟值均大于测量值;在横向速度预测中,SSTκ-ω模型展现了较大优势,与测量值吻合程度明显高于其他3种模型.