层次分析法在A*中的运用
2020-03-24聂宸菡
聂宸菡
(北京建筑大学 测绘与城市空间信息学院,北京100044)
当发生油气管道发生事故时,将不可避免地会对社会、环境等造成损害。建立应急救援系统是减少造成损害的有效方法,其中紧迫性是最显着的特征。当救援物资要求以最短时间到达事故现场时,决策者必须选择最佳路径,因此有人提出了启发式搜索算法: A*算法[1]。层次分析法(AHP)是由Saaty 开发的一种多标准决策(MCDM)技术,用于复杂的决策问题。 它采用多层次的层次结构,最终目标和实现这一目标的替代方案。AHP 不仅可以帮助决策者制定正确的决策,而且可以帮助他们找到最适合他们需求的解决方案以及他们对问题的理解[2]。在本文中,我们使用AHP 方法分析和比较影响最佳路线选择的四个阻抗因子,并给出每个因子的权重(优先级)。 然后,我们为研究区域的道路网络中的每个路段分配了权重值,通过使用该权重值而不是经典算法的距离权重值来改变经典A*算法。
1 A*算法
A*算法属于一种最经典的启发式搜索算法之一,是建立在Dijkstra 和BFS 算法基础上的,也属于遍历搜索算法,但因为采用了启发式方法来估计地图上任意点到目标点的代价, 从而可以智能地评估每个相关节点,只按照最可能最正确的方向去搜索,而忽略其他不相关的节点或者背离目标节点的方向。A*算法引入了当前节点n 的启发函数f(n),当前节点n 的启发函数定义为:
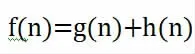
其中g(n)是从起点到当前节点n 的实际费用的量度,h(n)是从当前节点n 到终点的最小费用的估计。
经典的A*算法中f 函数的构造为距离权重为主,而在实际寻找最佳路径中,大多数使用距离作为权重来解决最佳路径问题,在紧急情况下选出最佳路径,必须考虑其他因素。分析这些元素所占比重,将用到层次分析法,下节将介绍层次分析法的步骤。
2 层次分析法
2.1 建立层次结构模型
首先,构建层次结构模型。模型中有三个级别:
(1)最高级别是引发的问题,称为目标级别。
(2)中间层是来自分解的复杂问题的元素,称为准则级别。
(3)最低级别是问题的度量和方案,称为方案级别。
在本文中,通过调查实时交通状况来选择阻抗因素。在我们的方法中,我们选择了影响最佳路径选择的四个阻抗因子:道路质量、交通流量、交通状况、天气。
2.2 成对比较
在层次分析法过程中,在确定各层次各因素之间的权重时,如果只是定性的结果,则常常不容易被别人接受,因此两两相互比较,对此时采用相对尺度,以尽可能减少性质不同的诸因素相互比较的困难,以提高准确度。(如表1 所示)。

表1 元素之间的相对重要性
2.3 建立比较矩阵
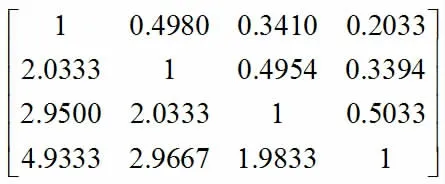
在进行两两比较后,输出的为一个比较矩阵,它包含了每对因素的比率,比较矩阵是nxn 矩阵,n 为因素数量。比较矩阵A为:

为了更接近实际状况,在上述所建立的比较矩阵中,每个元素采用三角模糊数构造的比较矩阵A 和道路数据调查分析出最小值和最大值取值,因此最终模糊比较矩阵Af为:
2.4 归一化、计算权重
通过使用几何平均方法对前一步骤的比较矩阵进行归一化来计算每个因素的总权重。如下等式:

其中aij是比较矩阵Af的元素值。
在计算归一化的比较矩阵之后,可以如下等式所示计算总权重向量。
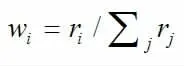
2.5 一致性检验
层次分析法的最后一步是计算成对比较矩阵的检验系数。检验系数(C.R.)是根据人为判断和感知衡量比较矩阵的一致性。如果C.R.<0.1 ,则认为该比较矩阵通过一致性检验,否则就不具有满意一致性。检验系数可以计算为:

λ 为比矩阵的最大特征值,用最大特征值对应的特征向量作为被比较因素对上层某因素影响程度的权向量。CI 越大,不一致越严重。由此可得比较矩阵最大特征值λ=4.0263,C.I.=0.0088,C.R.=0.0097。根据结果,当C.R. <0.10 时,比较矩阵的一致性是可以接受的,否则应该修改比较矩阵。所以Af是可以接受的,对应于A 的最大特征值的单位特征向量为:
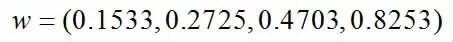
因此得出影响程度的大小顺序为:交通状况、交通流量、道路质量和天气状况。
2.6 权重的运用
在通过一致性检验后,计算出阻抗因素权重向量,将使用此权重向量计算出每条路线的总权重,把总权重代替经典A*算法中权重因子[4]。但由于各个阻抗因素的测量单位不一致,因此需要对阻抗因素进行归一化。为了更接近实际情况,每个阻抗因素需根据实际情况采用不同的方式进行归一化,如天气因素所占比重低,说明在进行归一化时需最小化来选择最佳路径。交通状况因素所占比重高,说明在进行归一化时需最大化来选择最佳路径。对于那些需要最大化的因素,归一化公式如下:
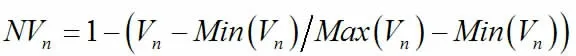
最小化所采取的的归一化公式:
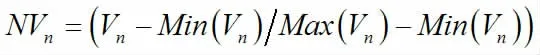
最终道路权重为:

3 实验与分析
本文利用改进的A*算法对交通网络图进行加权搜索。测试的地图,包括周边城市区域,来自于地理信息系统。搜索结果如下所示:

表2 结果对比
我们改进了经典的A*算法,将其权重因子替换为层次分析法法中的总权重因子。此外,我们还对改进后的算法进行了测试,并与经典的A*算法进行了比较。结果表明,该方法比经典的A*算法更有效。
