一种交叉与变异操作互斥的自适应遗传算法

张军

（华北电力大学，北京102206）

遗传算法是由美国密歇根大学的John H. Holland 教授及其学生于1975 年提出的，由于其具有高效，实用，鲁棒性强等特点，在机器学习，模式识别，控制科学等领域得到广泛的应用。目前大量的实践，研究表明，经典的遗传算法存在着局部搜索能力差，早熟等缺点，不能保证算法最终收敛，大量的文献[1][2]对遗传算法提出了一系列的改进，主要集中在操作算子方面。本文将算法中的交叉和变异操作设置为互斥关系，且将交叉概率设定为一个随着种群分布动态变化，通过仿真对比实验对结论进行分析。

1 遗传算法操作算子

1.1 选择算子

1.2 交叉算子

在种群进行选择操作后，将其分为A,B 两个部分：

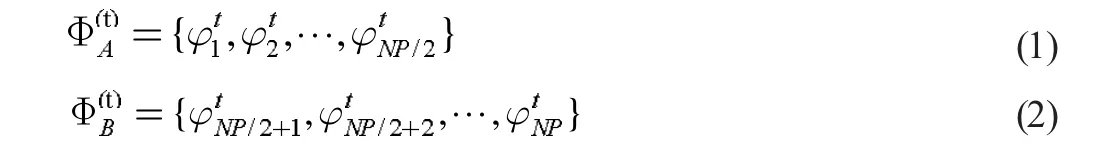
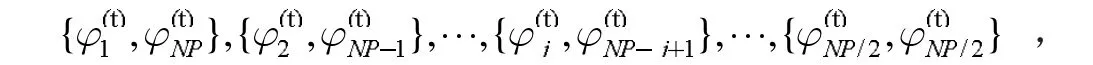
配对好的种群由NP/2 对个体组成。在进行交叉操作之前，需要先生成交叉概率pc：

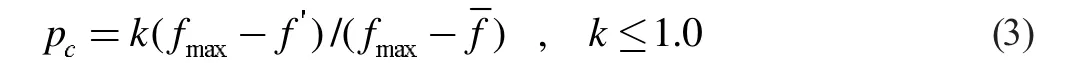
其中：f 是种群中适应度值最优的个体，f' 是配对的两个种群中适应度较大的个体，f 是种群的平均适应度值。

对于A 组中的个体实施：

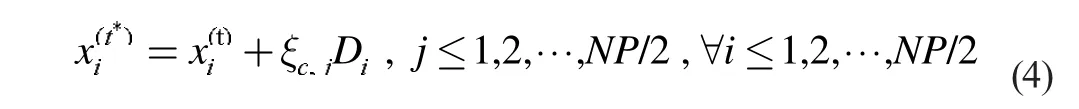
对于B 组中的个体实施:

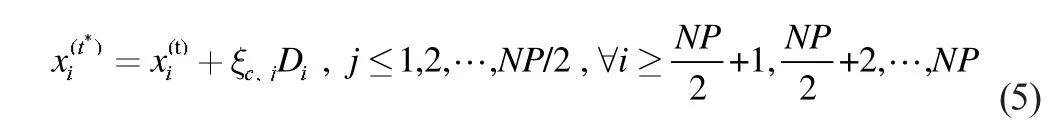
其中：

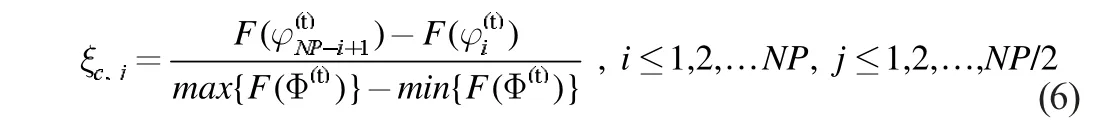
(b)Di为基于杂交配对组获取的优化方向信息，按照如下规则计算：

1.3 变异算子

本算法中变异算子与交叉算子为互斥关系，算法的寻优则有交叉操作完成，局部寻优由变异操作完成，显著强化算法的收敛能力。变异操作主要按照如下的形式完成：

(a)对A 组中的个体实施：

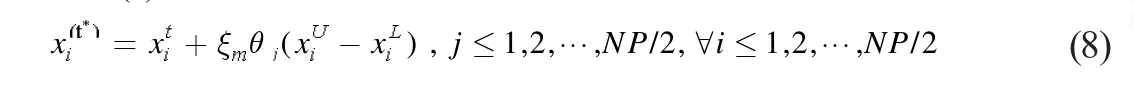
(b)对B 组中的个体实施：

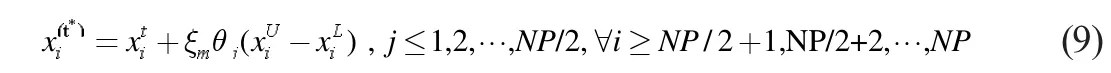
其中：

1.4 算法流程图（图1）

2 算法仿真

本文的仿真选取经典的Schaffer 测试函数：

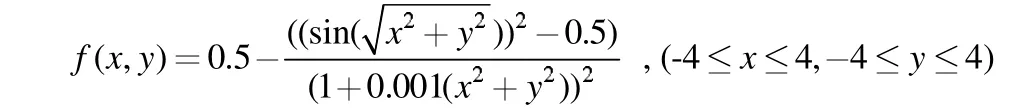
通过多次对算法进行仿真，结果如图2-3 所示。

3 仿真结果分析

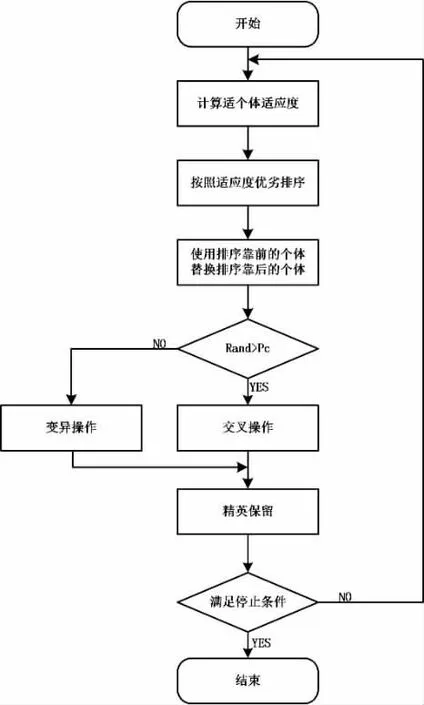
图1 算法流程图

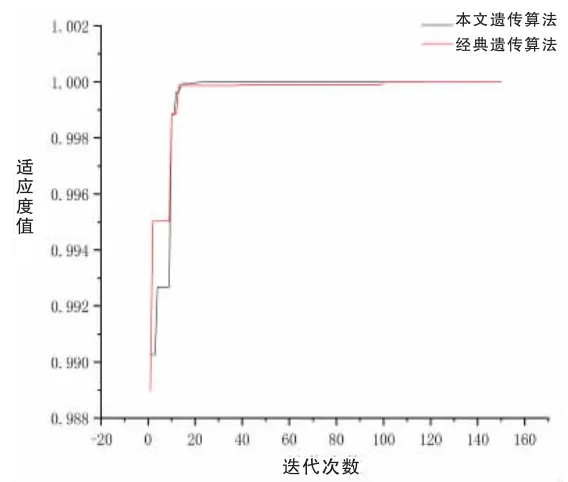
图2 适应度曲线

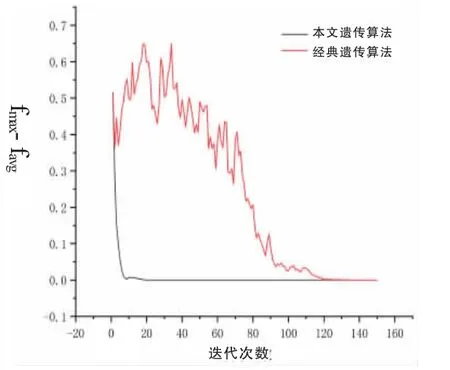
图3 种群一致性曲线

结束语

本文通过对改进的遗传算法和经典的遗传算法进行仿真与对比分析，证明了通过调整算法框架和改进操作算子，能够对算法的寻优能力进行较大的提升，获得更好的性能。