离心率——经久不衰的高考热点

王勇 龚俊峰

摘 要：离心率是历年高考的热点内容，涉及巧求离心率的值、界定离心率的范围、探究离心率的最值、借用离心率交汇整合等，本文结合典型例题予以分类导析，旨在探索题型规律，揭示解题方法.

关键词：离心率;经久不衰;高考热点

离心率是圆锥曲线中的一个重要元素，它的变化会直接导致曲线形状甚至类型的变化，同时它还是圆锥曲线统一定义中的三要素之一近年来，涉及离心率的问题频频出现在高考试题和各省市高考模拟试题中，且题型不断翻新，显示出旺盛的生命力！解决有关离心率的问题，除了要求对离心率的概念、几何意义深刻领会外，还常常要用到其它有关知识，因而，涉及离心率的问题不仅具有很强的综合性，而且其解法极富灵活性下面给出八道例题并予以分类解析，供参考.

1 巧求离心率的值

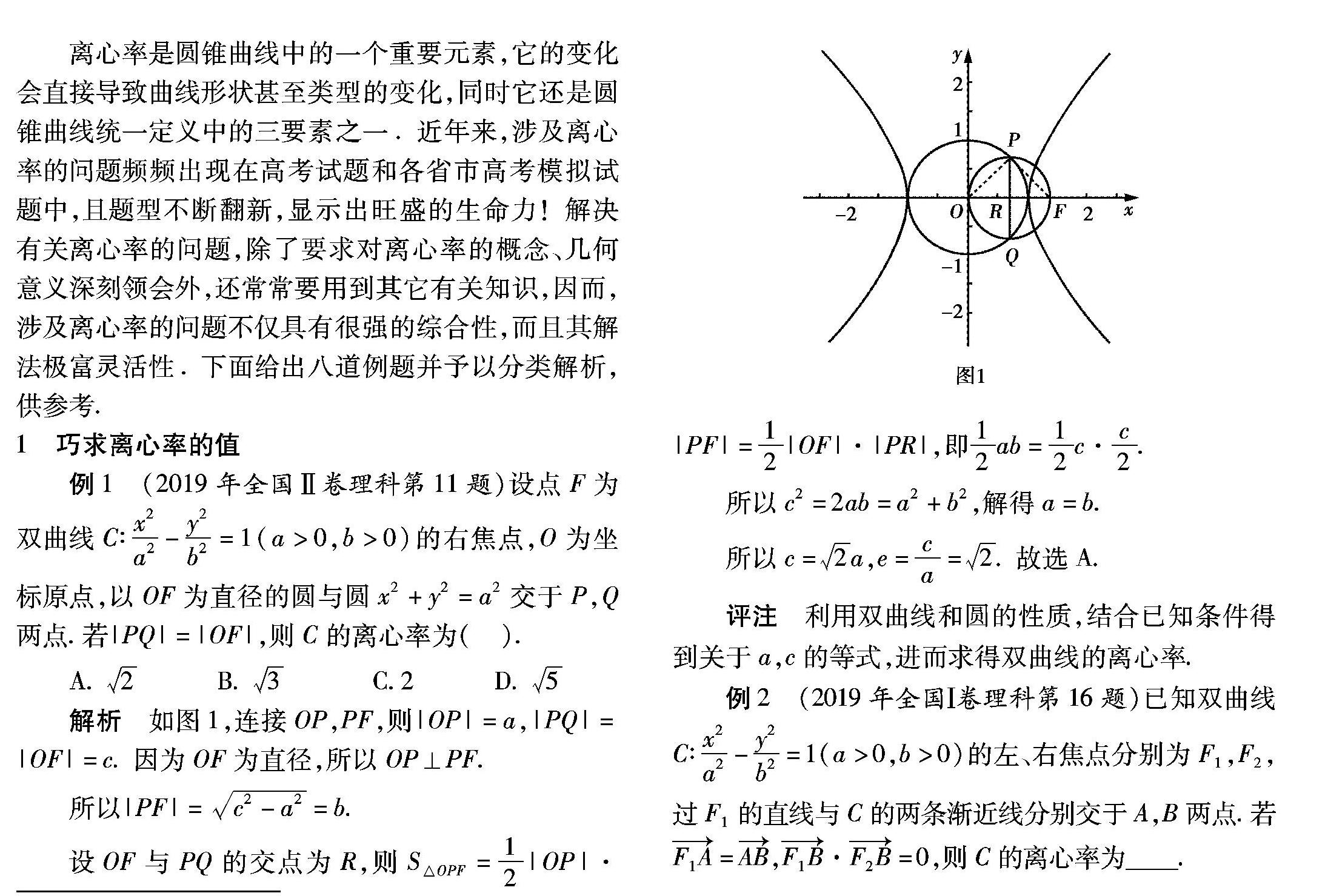
例1 （2019年全国Ⅱ卷理科第11题）设点F为双曲线C∶x2a2-y2b2=1（a>0，b>0）的右焦点，O为坐标原点，以OF为直径的圆与圆x2+y2=a2交于P，Q两点.若|PQ|=|OF|，则C的离心率为（ ）.

A 2 B 3C2 D 5

解析 如图1，连接OP，PF，则|OP|=a，|PQ|=|OF|=c因为OF为直径，所以OP⊥PF.

所以|PF|=c2-a2=b.

设OF与PQ的交点为R，则

S△OPF=12|OP|·|PF|=12|OF|·|PR|，即12ab=12c·c2

所以c2=2ab=a2+b2，解得a=b.

所以c=2a，e=ca=2故选A.

评注 利用双曲线和圆的性质，结合已知条件得到关于a，c的等式，进而求得双曲线的离心率.

例2 （2019年全国Ⅰ卷理科第16题）已知双曲线C∶x2a2-y2b2=1（a>0，b>0）的左、右焦点分别为F1，F2，过F1的直线与C的两条渐近线分别交于A，B两点.若F1A=AB，F1B·F2B=0，则C的离心率为.

解法1 如图2，因为F1B·F2B=0，所以F1B⊥F2B.

在Rt△F1BF2中，|OB|=|OF2|.

所以∠OBF2=∠OF2B.

又因为F1A=AB，所以A为F1B的中点.

所以OA//F2B所以∠F1OA=∠OF2B.

因为∠F1OA=∠BOF2，所以∠OBF2=∠OF2B=∠BOF2.

所以△OBF2为等边三角形.

由F2（c，0）可得Bc2，3c2.

因为点B在直线y=bax上，所以3c2=ba·c2.

所以ba=3.

所以e=1+b2a2=1+32=2.

解法2 如图2，因为F1B·F2B=0，所以F1B⊥F2B.

所以|OF1|=|OB|.

所以∠BF1O=∠F1BO.

所以∠BOF2=2∠BF1O.

因为F1A=AB，所以点A为F1B的中点.

又点O为F1F2的中点，所以OA//BF2.

所以F1B⊥OA.

因为直线OA，OB为双曲线C的两条渐近线，

所以tan∠BF1O=ab，tan∠BOF2=ba.

因为tan∠BOF2=tan（2∠BF1O），

所以ba=2×ab1-ab2.

所以b2=3a2.

所以c2-a2=3a2，即2a=c，

所以雙曲线的离心率e=ca=2.

评注 破解本题的关键是细审题、画草图、会转化，可以转化为证明△OBF2为正

三角形，从而得出点B的坐标，再代入点B所在直线的方程求解（如解法1）;

也可以往角转化，再利用二倍角的正切公式求解（如解法2），后续只需认真运算即可轻松获解.

2 界定离心率的范围

例3 （2019年青岛市模拟题）已知直线l∶y=kx与椭圆C∶x2a2+y2b2=1（a>b>0）交于A，B两点，F为椭圆C的左焦点，且AF·BF=0，若∠ABF∈0，π12，则椭圆C的离心率e的取值范围为（ ）.

A0， 22 B0， 63

C 22， 63D 63，1

解析 如图3，设椭圆C的右焦点为F′，连接AF′，BF′.

因为AF·BF=0，所以AF⊥BF.

又直线l∶y=kx过原点O，所以根据椭圆的对称性知点A，B关于原点对称，所以四边形AFBF′是矩形.

所以AB=FF′=2c（其中c=a2-b2）.

在Rt△AFB中，设∠ABF=θ，则AF=ABsinθ=2csinθ，BF=ABcosθ=2ccosθ.

又根据椭圆的定义知AF+AF′=AF+BF=2a.

所以2csinθ+2ccosθ=2a.

所以离心率e=ca=1sinθ+cosθ=1 2sin（θ+π4）.

又θ∈0，π12，所以π4<θ+π4≤π3.

所以 22

所以 63≤1 2sin（θ+π4）<1，即e∈ 63，1

故选D.

评注 本题在几何构图的基础上引入角变量，将所给问题转化为三角函数的值域问题，求解时必须注意自变量θ的取值范围.

例4 （2019年福州市质检题）已知双曲线x2a2-y2b2=1（a>0，b>0），A1，A2是实轴端点，F是右焦点，B（0，b）是虚轴端点，若在线段BF上（不含端点）存在不同的两点Pi（i=1，2），使得△PiA1A2（i=1，2）构成以A1A2为斜边的直角三角形，则双曲线的离心率e的取值范围是（ ）.A 2，+∞.

A2，+∞ B 5+12，+∞

C1， 5+12 D 2， 5+12

解析 易得直线BF的方程为bx+cy-bc=0.

由于在线段BF上（不含端点）存在不同的两点Pi（i=1，2），使得△PiA1A2（i=1，2）构成以A1A2为斜边的直角三角形，说明以A1A2为直径的圆C与线段BF（不含端点）有两个不同的交点.

画图易知，首先要满足a 2，另外还要满足原点到直线BF的距离小于圆C的半径a，即bc b2+c2

整理，得b4

亦即e2-e-1<0，注意到e> 2，解得 2

评注 本题将几何条件转译为代数不等式求解，考查了转化与化归思想求解本题极易漏掉a

3 探寻离心率的最值

例5 （2019年保定市模拟题）已知圆O1的圆心为（2，0），半径为4;圆O2∶x2+y2=r2（0e2），则2e1+3e2的最小值为.

A5+2 64B32C 2 D38

解析 依题意，圆O1的方程为（x-2）2+y2=16，设动圆M的半径为R.

（1）当动圆与两定圆都内切时，如图4所示，则MO1=4-R，MO2=R-r所以MO1+MO2=4-r.

此时，点M的轨迹为以O1，O2为焦点的椭圆，且2a=4-r，2c=O1O2=2，故其离心率为24-r.

（2）当动圆与两定圆分别内切、外切时，如图5所示，则MO1=4-R，MO2=R+r所以MO1+MO2=4+r.

此时，点M的轨迹为以O1，O2为焦点的椭圆，且2a′=4+r，2c′=O1O2=2，故其离心率为24+r.

注意到e1>e2，所以e1=24-r，e2=24+r

因为1e1+1e2=4，

故2e1+3e2=14（2e1+3e2）（1e1+1e2）=14（5+2e1e2+3e2e1）≥5+2 64，当且仅当 2e1=3e2时等号成立.

所以2e1+3e2min=5+2 64.故选A.

评注 本题考查动点轨迹的求法、基本不等式的应用分析得出1e1+1e2=4并利用常数代换法是求解问题的关键本题考查数形结合思想、分类讨论思想和运算求解能力.

例6 （2014年湖北卷理科第9题）已知F1，F2是椭圆和双曲线的公共焦点，点P是它们的一个公共点，且∠F1PF2=π3，则椭圆和双曲线的离心率的倒数之和的最大值为（ ）.

A4 33 B2 33 C3 D2

解法1 利用椭圆、双曲线的定义和几何性质求解.

设PF1=r1，PF2=r2r1>r2，F1F2=2c，椭圆长半轴长为a1，双曲线实半轴长为a2，椭圆、双曲线的离心率分别为e1，e2，由2c2=r21+r22-2r1r2cosπ3，得4c2=r21+r22-r1r2.

由r1+r2=2a1，r1-r2=2a2，解得r1=a1+a2，r2=a1-a2

所以1e1+1e2=a1+a2c=r1c.

令m=r21c2=4r21r21+r22-r1r2=41+r2r12-r2r1=4r2r1-122+34，

当r2r1=12时，mmax=163，所以r1cmax=4 33.

即1e1+1e2的最大值为4 33故选A.

解法2 利用椭圆、双曲线的定义和几何性质，柯西不等式求解.

设PF1=r1，PF2=r2，F1F2=2c，椭圆长半轴长为a1，双曲线实半轴长为a2，椭圆、双曲线的离心率分别为e1，e2.

依题意得2c2=r21+r22-2r1r2cosπ3，①

在椭圆中，①式化简得4c2=4a21-3r1r2.

所以3r1r24c2=1e21-1②

在双曲线中，①式化简得4c2=4a22+r1r2.

所以r1r24c2=-1e22+1 ③

联立②③得1e21+3e22=4.

由柯西不等式得

1+13 1e21+3e22 ≥1×1e1+1 3× 3e22.

解得1e1+1e2≤4 33，当且仅当e1= 33，e2=3时等号成立，所以1e1+1e2的最大值为4 33故选A.

评注 本题综合考查椭圆、双曲线的定义，离心率，余弦定理，二次函数，柯西不等式等由余弦定理得到2c2=r21+r22-2r1r2cosπ3，考查函数与方程的思想;再利用椭圆、双曲线的定义得到4c2=4a21-3r1r2，4c2=4a22+r1r2，考查转化与化归的思想;由二次函数或柯西不等式求离心率的倒数之和的最大值，考查运算求解能力、推理论证能力本题难度较大，充当着“小题把关”的重要角色.

4 借用离心率交汇整合

例7 （2019年湖南师大附中模拟题）在等腰梯形ABCD中，AB//CD，且AB=2，

AD=1，CD=2x，其中x∈0，1，以A，B为焦点且过点D的双曲线的离心率为e1，以C，D为焦点且过点A的椭圆的离心率为e2，若对任意x∈0，1，不等式t

A 3 B 5 C2 D 2

解析 在等腰梯形中易求得DB=AC=4x+1.如图6，设双曲线的实半轴长为a1，则2a1=DB-AD=4x+1-1如图7，设椭圆的长半轴长为a2，则2a2=AD+AC=4x+1+1.

所以e1+e2=1a1+xa2=2 1+4x-1+2x1+ 1+4x

= 1+4x+12x+2x1+ 1+4x.

令m=fx= 1+4x+12x=12 1x2+4x+1x，则fx在0，1上单调递减，所以m>f1= 5+12.

又函數gm=m+1m在 5+12，+∞上单调递增，所以gm>g 5+12= 5+12+2 5+1=5，即e1+e2> 5.

若对任意x∈0，1，不等式t

评注 本题考查双曲线和椭圆的定义及几何性质、函数的单调性、不等式恒成立问题等根据双曲线和椭圆的定义结合离心率公式得到表达式，利用函数的单调性及不等式恒成立原理求得t≤ 5，进而求出t的最大值.

例8 （2019年石家庄市模拟题）如图8所示，一个圆柱形乒乓球筒，高为20厘米，底面半径为2厘米球筒的上底和下底分别粘有一个乒乓球，乒乓球与球筒底面及侧面均相切（球筒和乒乓球厚度均忽略不计）一个平面与两个乒乓球均相切，且此平面截球筒边缘所得的图形为一个椭圆，则该椭圆的离心率为（ ）.

A 154 B15

C2 65 D14

解析 如图9，设上、下两个乒乓球的球心分别为O1，O2，椭圆与球筒边缘的交点分别为E，F，椭圆与两个乒乓球的切点分别为A，B，由题可知，O1O2=16，O1A=2.

过点E作EM⊥O1O2于点M，则EM=O1A=2.

易知△EMO≌△O1AO.

则EO=O1O=8.

所以EF=16.即椭圆的长轴长2a=16，a=8.

椭圆的短轴长为圆柱的底面直径，即2b=4，b=2.所以c=a2-b2=2 15.

故该椭圆的离心率e=ca= 154故选A.

评注 本题将立体几何和解析几何有机交汇在一起，立意新颖在图形的引领下，充分利用平面几何知识和离心率的计算公式而获解本题难度较大，有较好的区分和选拔功能，对考生空间想象能力、转化与化归能力要求较高.

参考文献：

[1]杜志建全国各省市高考冲刺优秀模拟试卷汇编[M].乌鲁木齐：新疆青少年出版社，2019.

[2]杜志建2020新编高考题库[M].延吉：延边教育出版社，2019.

[3]薛金星2019年全国及各省市高考试题全解[M].西安：陕西人民教育出版社，2019.

（收稿日期：2019-08-30）