窄基角钢输电塔风振系数研究

罗正帮, 肖俊俊, 谭谨林, 张 壮, 王梦博, 牛忠荣

(1.安徽华电工程咨询设计有限公司,安徽 合肥 230022; 2.合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

0 引 言

随着我国城镇化进程的加快,城镇规划区及城市郊区的线路走廊日趋紧张,常规输电塔由于占地较大,难以满足城镇狭窄走廊输电线路要求。因此,占地面积小,且适用于110 kV以上高压输电的窄基角钢塔得到了广泛的运用。而该类窄基输电塔不但塔高较高且根开比一般输电塔小,属于高柔结构,受风荷载作用影响明显,对该类结构进行风荷载作用下的结构动力响应分析是十分重要的。

在输电塔的抗风设计中,风振系数βz是计算风荷载的重要参数。依据现有规范《架空输电线路杆塔结构设计技术规定》(DLT 5154—2012)[1]规定,在计算塔架风荷载时,当塔高不超过60 m时,风振系数统一取值;当塔高超过60 m时,风振系数可依照《建筑结构荷载规范》(GB 50019—2012)[2]从下到上进行分段计算。文献[1]只适用于根开比为4～6的塔架,文献[2]只适用于外形和质量连续变化的结构,但窄基角钢输电线塔显然不满足上述要求。为此,文献[3-5]分别采用时域和频域分析方法进行了输电塔等空间钢结构的风振系数计算,模拟了等效静力风载荷。但是,这2种方法需要计算的数据较多,且时域法的计算过程复杂,耗时长,不利于工程实践。因此,获得一种简单的方法以确定输电塔结构的风振系数,解决窄基塔的设计难点十分必要。

本文以中国华东电网某输电线路上4座不同型号的窄基角钢输电塔为研究对象,通过利用谐波合成法模拟输电塔的风荷载,进行了不同输电塔的动力时程分析,依据风振响应计算结果对输电塔风振系数进行了计算,并与依据随机振动理论、文献[1-2]计算得到的风振系数结果进行了对比。在此基础上,通过拟合提出了窄基角钢输电塔风振系数的简化计算公式,为类似窄基角钢输电塔的设计提供参考。

1 有限元模型及动力特性分析

1.1 工程简况

本文研究对象为中国华东电网某110 kV输电线路上4座典型的窄基角钢输电塔,包括1座直线塔、1座耐张塔及某110 kV+35 kV+10 kV混压输电线路上的1座直线塔和1座耐张塔,前2座塔为双回路窄基塔,塔高、根开比分别为46.4 m、15.5与38.2 m、12.7,后2座塔为六回路窄基塔,塔高、根开比分别为68.4 m、19.5与53.8 m、15.4,各塔详细参数见表1所列。4座窄基塔主材及横担均采用Q345角钢,斜材及其他辅材采用Q235角钢,塔身不同高度处钢材截面尺寸不一,4根塔柱为结构主要受力构件,各段构件采用端部螺栓连接,塔架与基础固接,4座窄基塔的立面图如图1所示。

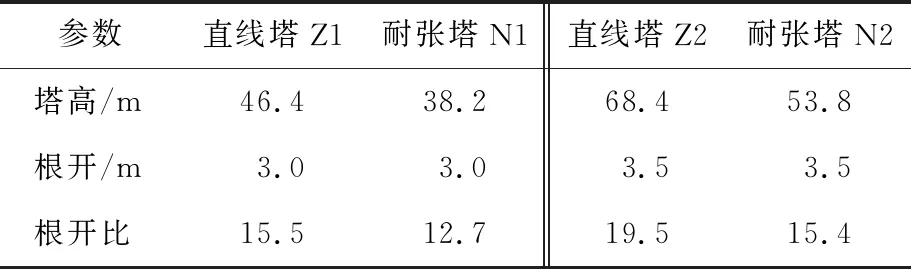
表1 4个窄基塔基本参数

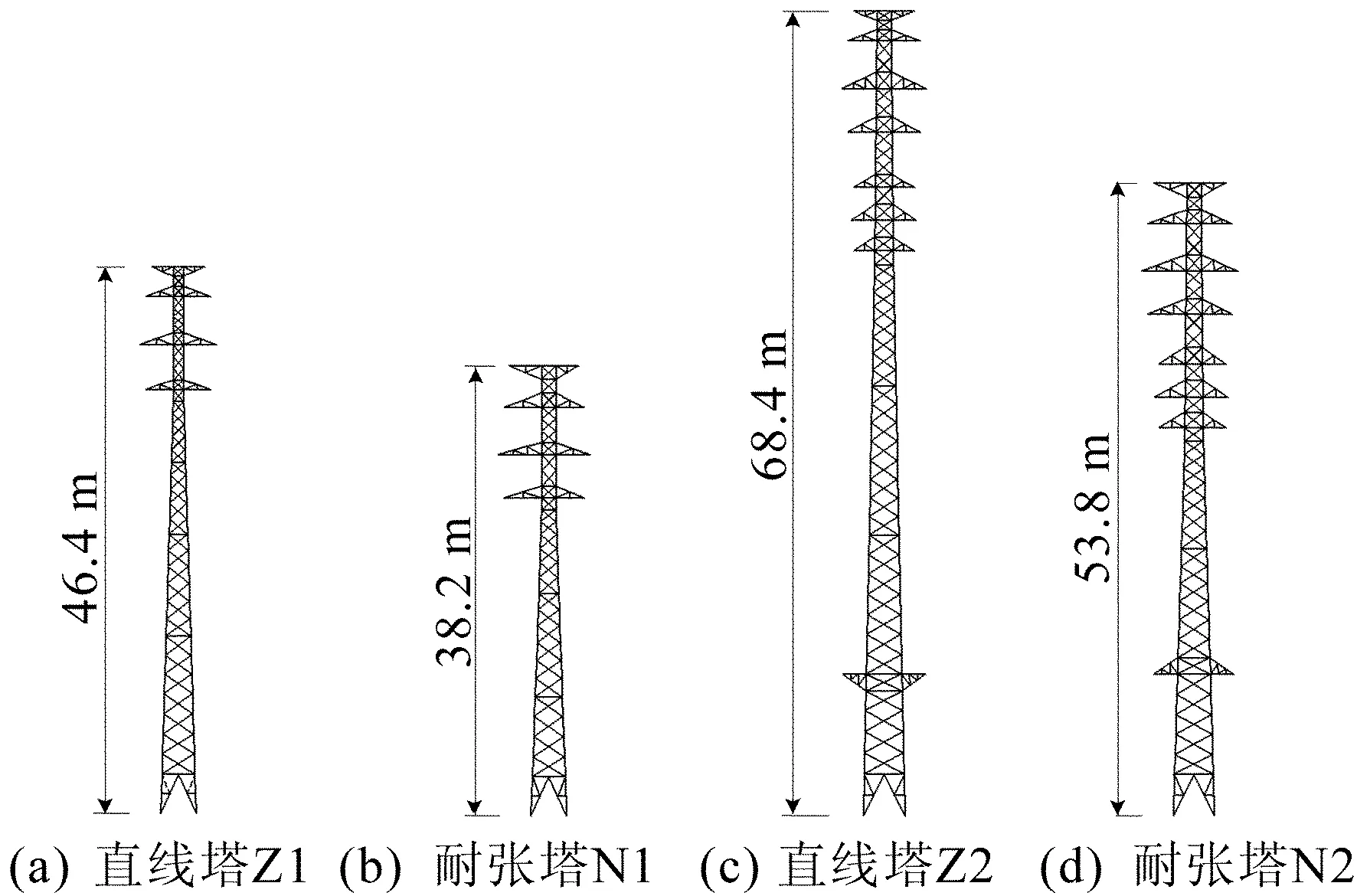
图1 窄基塔立面图

1.2 动力特性分析

考虑到角钢塔结点采用多个螺栓连接方式,对窄基角钢塔建立合理的力学模型,依据已有研究结果,进行杆塔结构的整体动力响应分析可采用梁-杆混合模型[6]。塔身主材、横担材及横隔材采用梁单元模拟,斜材以及辅材采用空间杆单元模拟,每根杆件作为一个单元[7]。约束窄基塔支座位移,采用Block Lanczos法进行模态分析。各窄基角钢塔模型的前6阶自振频率及振型结果见表2所列。由表2可知,窄基角钢塔高度越高,结构越柔,其固有频率越小。

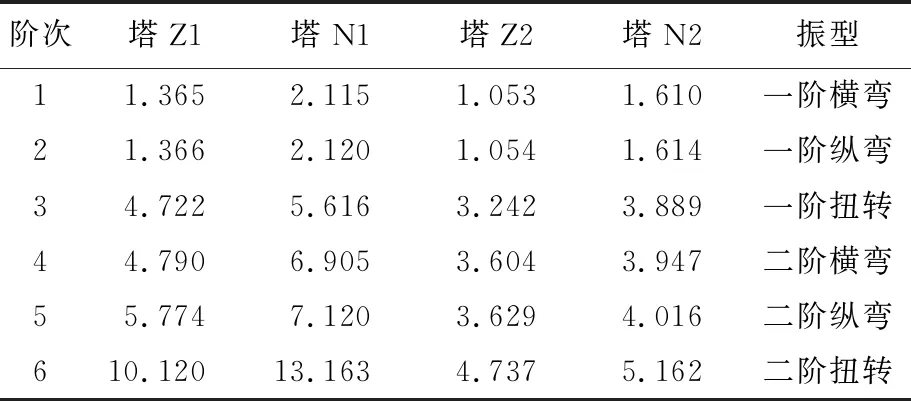
表2 结构前6阶自振频率及振型

2 风振系数计算方法

2.1 规范取值

文献[1]中规定对于杆塔本身,当全高不超过 60 m 时,风振系数可以采用同一值,具体取值见表3所列。

表3 杆塔风荷载调整系数

注:中间值按插入法计算;对自立式杆塔,表中数值适用于高度与根开之比为4～6。

文献[2]规定的风振系数计算公式为:

(1)

其中，g为峰值因子,取2.5;I10为10 m高度名义湍流强度,对应A、B、C和D类地面粗糙度,分别取0.12、0.14、0.23、0.39;R为脉动风荷载的共振分量因子;Bz为脉动风荷载的背景分量因子。

2.2 随机振动理论

脉动风是一种典型的随机荷载,由它引起的结构顺风向振动自然也是一种随机振动过程,因此结构顺风向风振响应分析可基于结构随机振动理论进行。在脉动风荷载Pd(z)作用下,结构的风振系数被定义为总风力P(z)与静风力Ps(z)的比值,则风振系数βz可表示为[8]：

(2)

实际工程中,对于类似悬臂结构常简化为多质点体系,考虑第一阶振型的影响。于是在只考虑第一振型的情况下,结构z高度处第k点由脉动风引起的等效惯性力Pdk为:

我国竹资源丰富，据初步统计有39属500多种，重点分布在长江以南的14个省区的丘陵山地，因而分布在黄河以北地区的为数不多的竹林资源就显得更珍贵。以河南省为例，参考河南农学院园林系竹子研究所发表的《河南竹类植物图志》[1]，河南省有70多个县产竹，毛竹、桂竹、乌哺鸡竹、淡竹、斑竹等都是河南省面积较大、分布较广、品质较优的乡土竹种。与南方相比，北方地区对竹林的研究和利用水平都较低，保护并发展北方地区竹林资源具有重要的生态价值、社会价值和经济价值。

(3)

其中，Mk为k点质量;ω1为结构第一阶固有频率;y1k为基于随机振动理论k点位移响应。

平均风引起的风荷载Psk的表达式为:

Psk=μsμzw0Ak

(4)

其中，μs为体型系数;w0为基本风压;Ak为k点受风面积。

2.3 时程分析法

本文采用Davenport[9]风谱作为模拟的目标谱,运用谐波合成法进行风速时程模拟,模拟获得的68.4 m塔高处的脉动风速时程曲线如图2所示。利用模拟获得的风速时程，计算作用于结构的风荷载，其计算公式为:

(5)

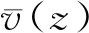
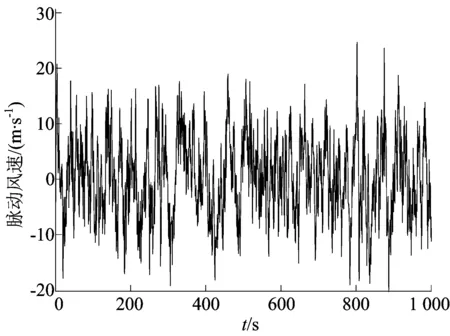
图2 68.4 m高度处的脉动风速时程

采用有限元法对各输电塔进行风振响应分析,根据其风振响应时程分析结果,采用风振系数进行计算，公式如下:

(6)

3 风振系数计算结果及简化计算

3.1 计算结果分析

本文采用动力时程分析方法、随机振动理论及相关规范计算得到的各输电塔风振系数计算结果分别见表4～表7所列,如图3～图6所示。

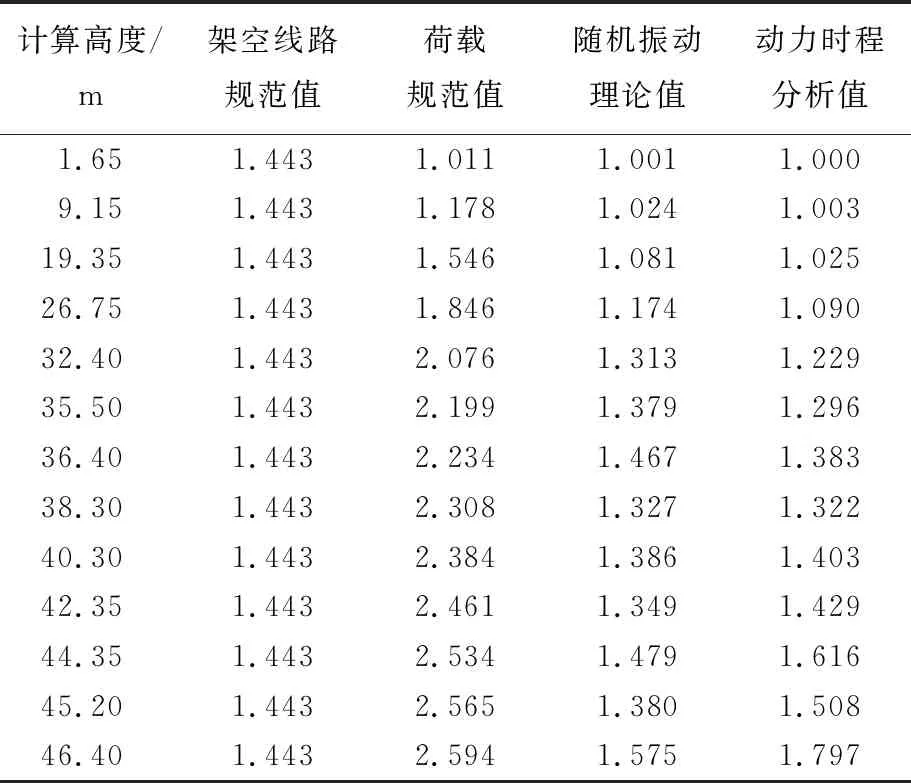
表4 直线塔Z1风振系数βz

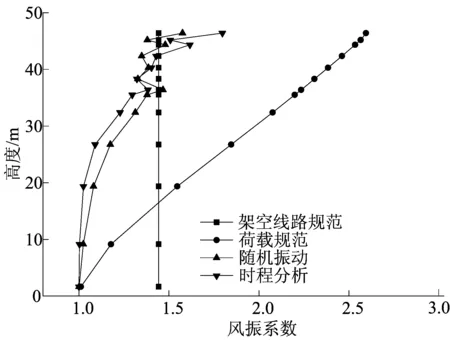
图3 直线塔Z1风振系数对比

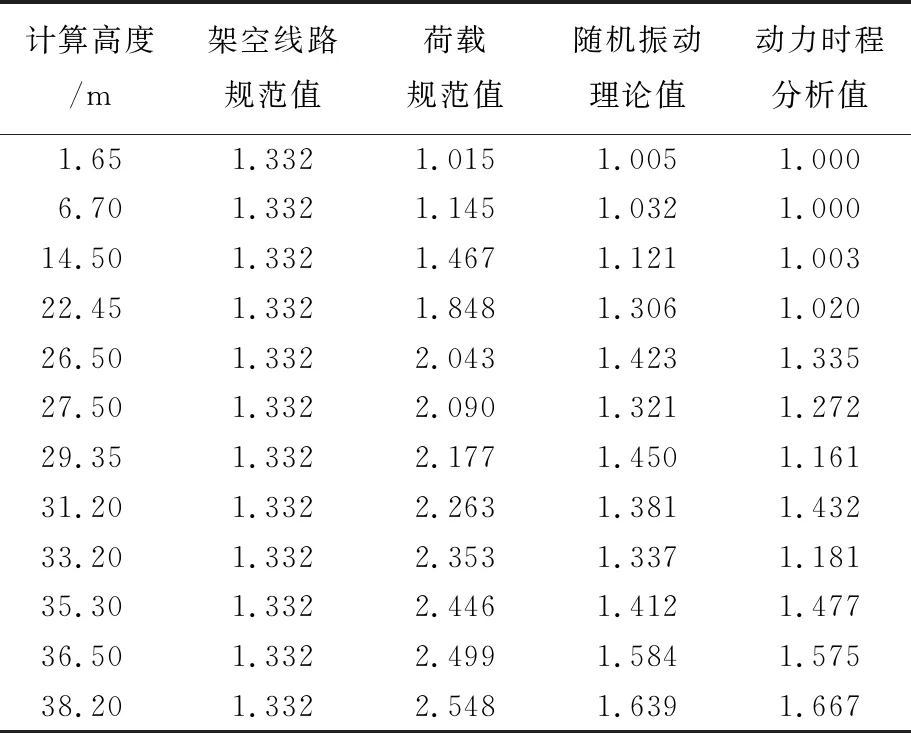
表5 耐张塔N1风振系数βz

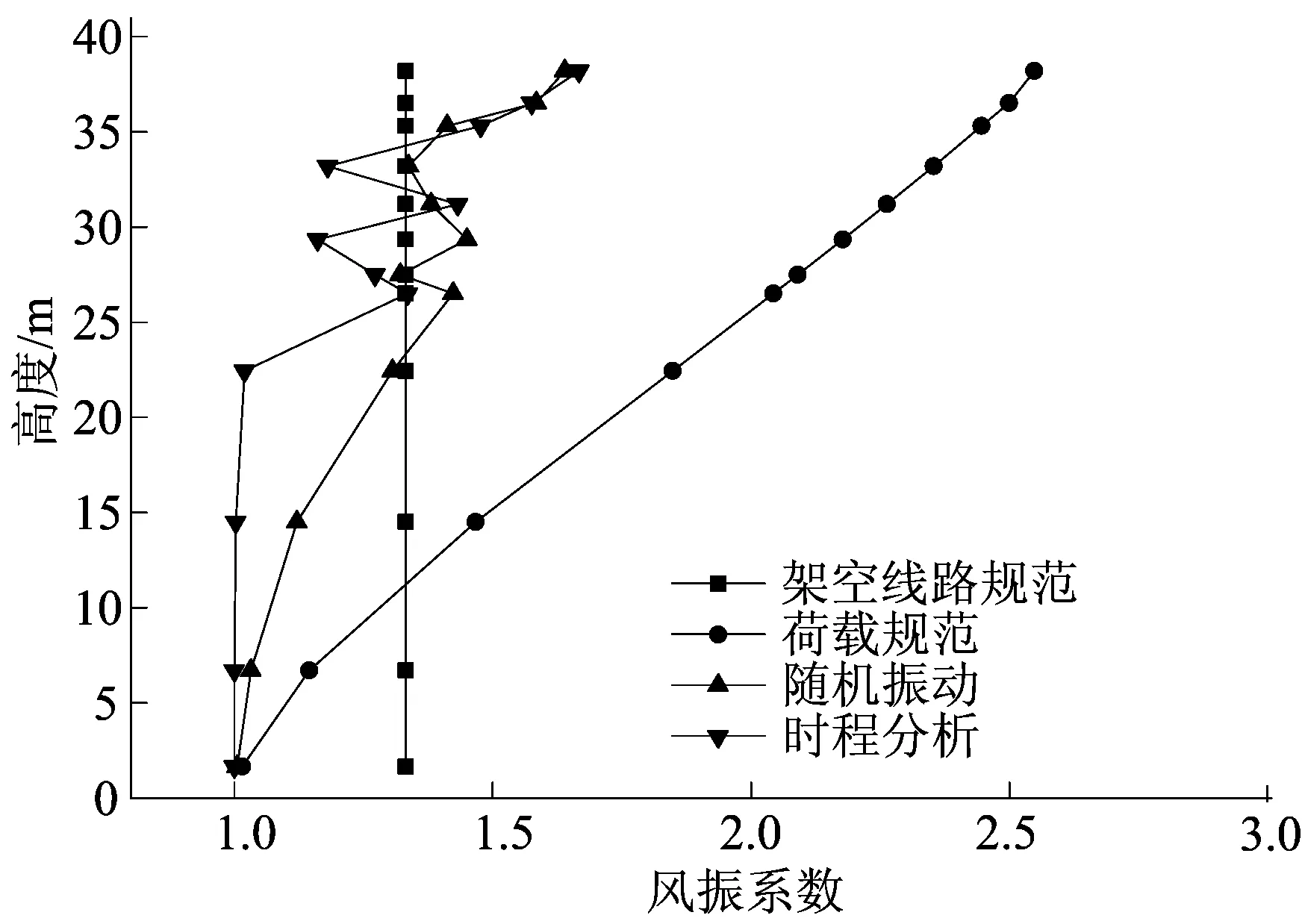
图4 耐张塔N1风振系数对比

由计算结果可知,对窄基塔来说,风振系数的变化是离散的,总体上来说风振系数随高度的增加而增大,从时程分析的计算结果可知，在横担处输电塔风振系数值会发生突变,这是由于横担的存在导致了其受风面积突变造成的。时程分析计算结果与随机振动理论的计算结果较为接近,而规范取值与之相比却有较大差别,其中架空线路规范取值结果在塔身下部取值偏大,在塔身上部不能反映塔身截面的变化。而荷载规范仅适用于外形、质量、刚度沿高度连续变化的高耸结构,对于输电塔这类格构式柔性塔架而言,风振系数计算结果明显偏大而不合理。同时,通过对不同类型窄基角钢塔的计算结果进行对比发现,由于耐张塔相比于直线塔而言其受力特性更为复杂,因此直线塔的风振系数计算值要明显大于耐张塔。以上分析结果表明,现有设计规范对风振系数取值的规则不适用于该类根开较小且外形变化较大的窄基角钢输电塔,这对窄基角钢塔的抗风设计有不利影响。因此,对于窄基角钢塔的设计分析应进行单独规定,且直线塔与耐张塔的风振系数取值应有所区别。

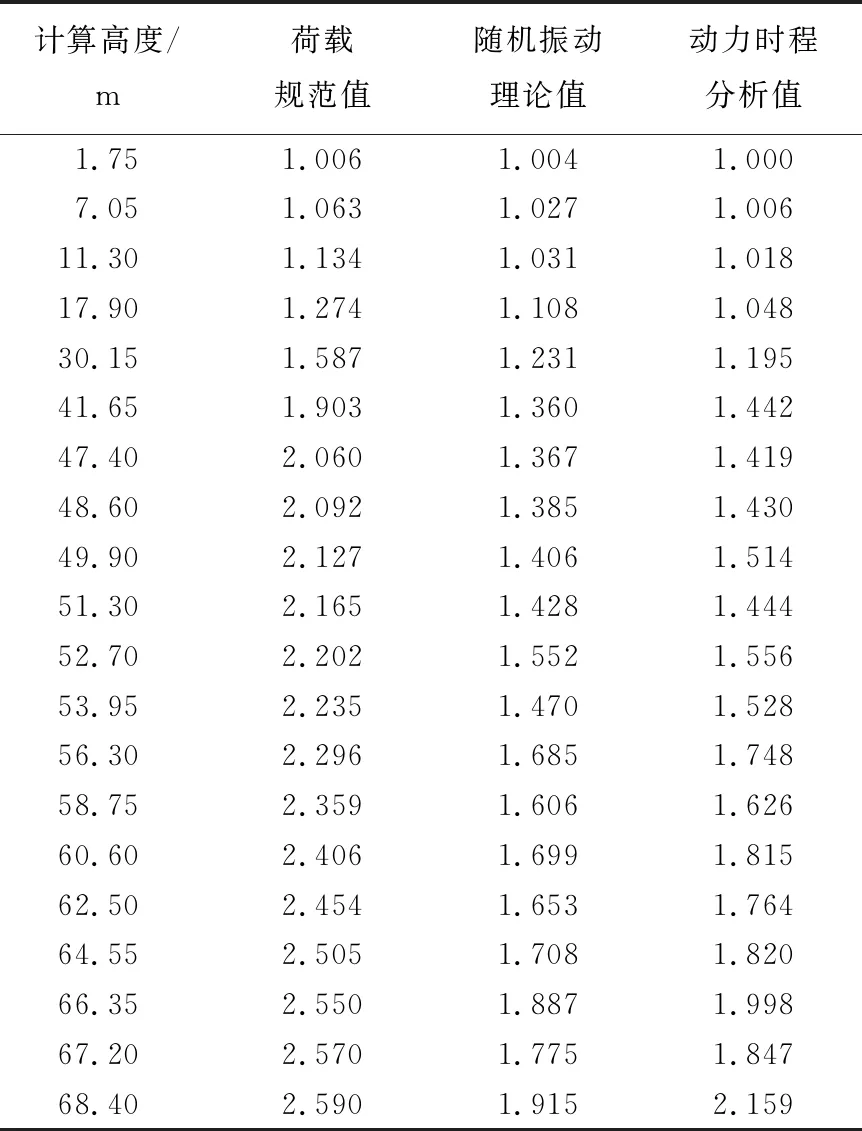
表6 直线塔Z2风振系数βz

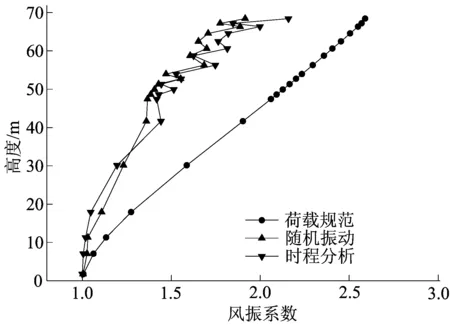
图5 直线塔Z2风振系数对比

表7耐张塔N2风振系数βz

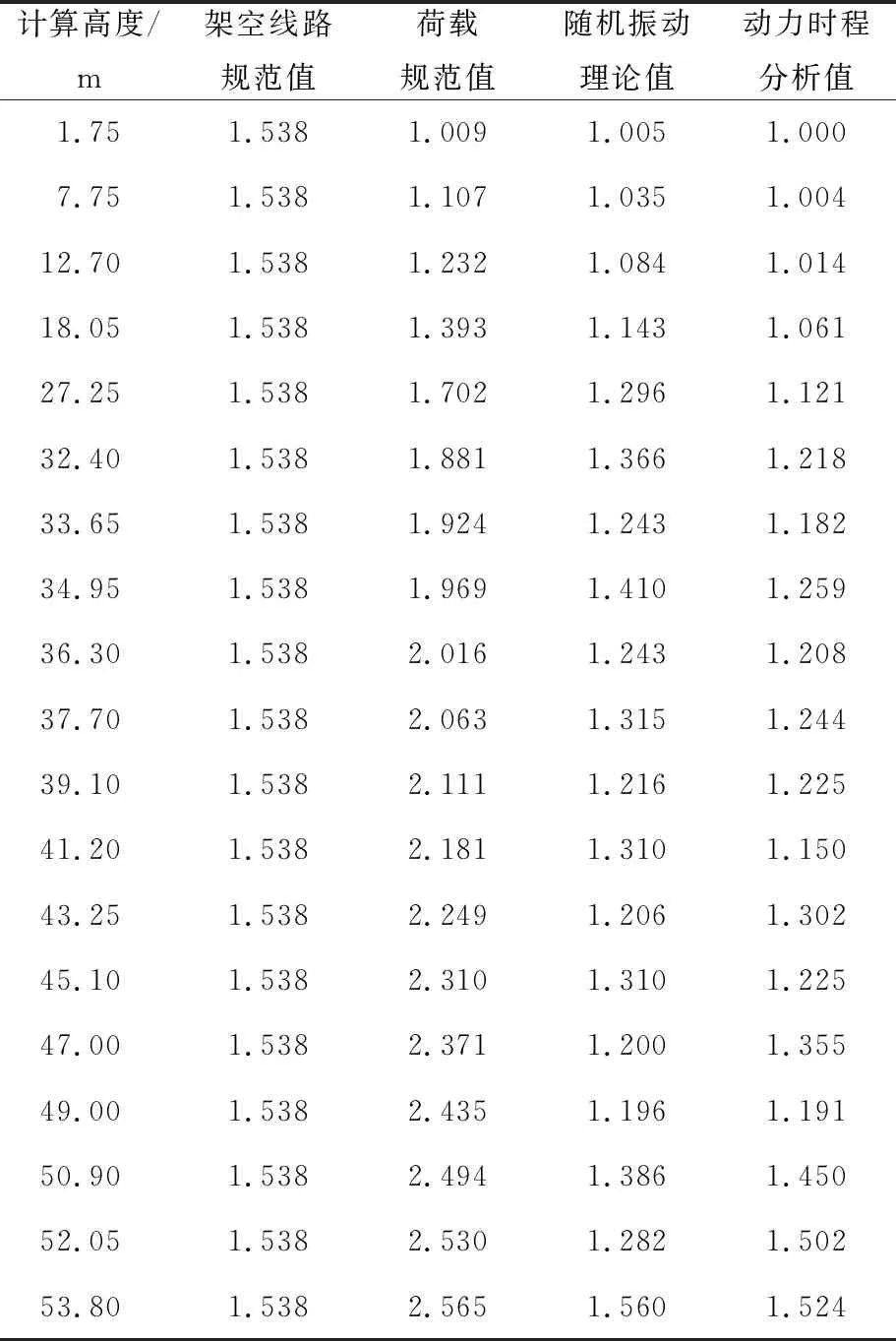
计算高度/m架空线路规范值荷载规范值随机振动理论值动力时程分析值1.751.5381.0091.0051.0007.751.5381.1071.0351.00412.701.5381.2321.0841.01418.051.5381.3931.1431.06127.251.5381.7021.2961.12132.401.5381.8811.3661.21833.651.5381.9241.2431.18234.951.5381.9691.4101.25936.301.5382.0161.2431.20837.701.5382.0631.3151.24439.101.5382.1111.2161.22541.201.5382.1811.3101.15043.251.5382.2491.2061.30245.101.5382.3101.3101.22547.001.5382.3711.2001.35549.001.5382.4351.1961.19150.901.5382.4941.3861.45052.051.5382.5301.2821.50253.801.5382.5651.5601.524

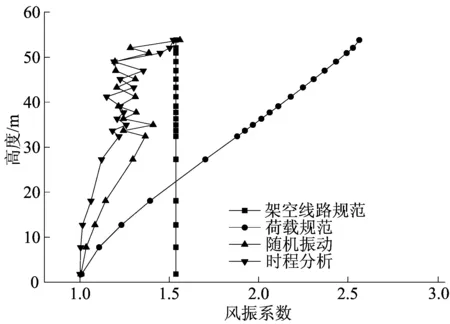
图6 耐张塔N2风振系数对比

3.2 简化计算公式

对窄基角钢塔,考虑到设计规范的不适用性及动力时程分析过程的复杂性,对窄基角钢塔的风振系数进行简化计算为工程实践提供方便显得尤为重要。根据时程分析方法计算得到的风振系数,在文献[10]研究基础上除考虑风振系数随高度变化外，同时考虑到窄基塔自身特征和截面突变对计算结果的影响。本文研究提出了窄基角钢塔风振系数分段拟合多项式方程,并通过数据拟合得到了直线型及耐张型窄基塔风振系数的简化计算公式。

(1) 直线型窄基角钢塔风振系数简化公式为:

(7)

(2) 耐张型窄基角钢塔风振系数简化公式:

(8)

其中，z为塔段中心高度;h为塔总高;B(z)为z高度处塔段迎风面宽度;B0为输电塔根开。

由(7)式、(8)式可知,窄基塔风振系数简化计算只与输电塔总高、各段中心高度、根开以及各段迎风面宽度有关,从而简化了输电塔风振系数的计算结果,便于角钢塔工程设计的应用。

为验证简化计算公式的可靠性,将时程分析的风振系数计算结果与简化计算公式结果进行了对比,如图7、图8所示。

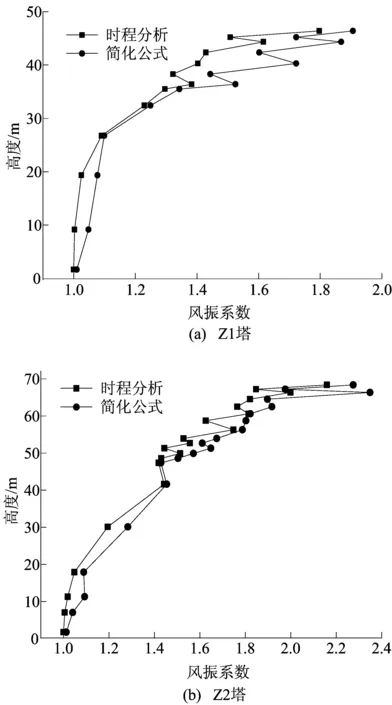
图7 直线塔简化计算公式与时程分析风振系数结果对比

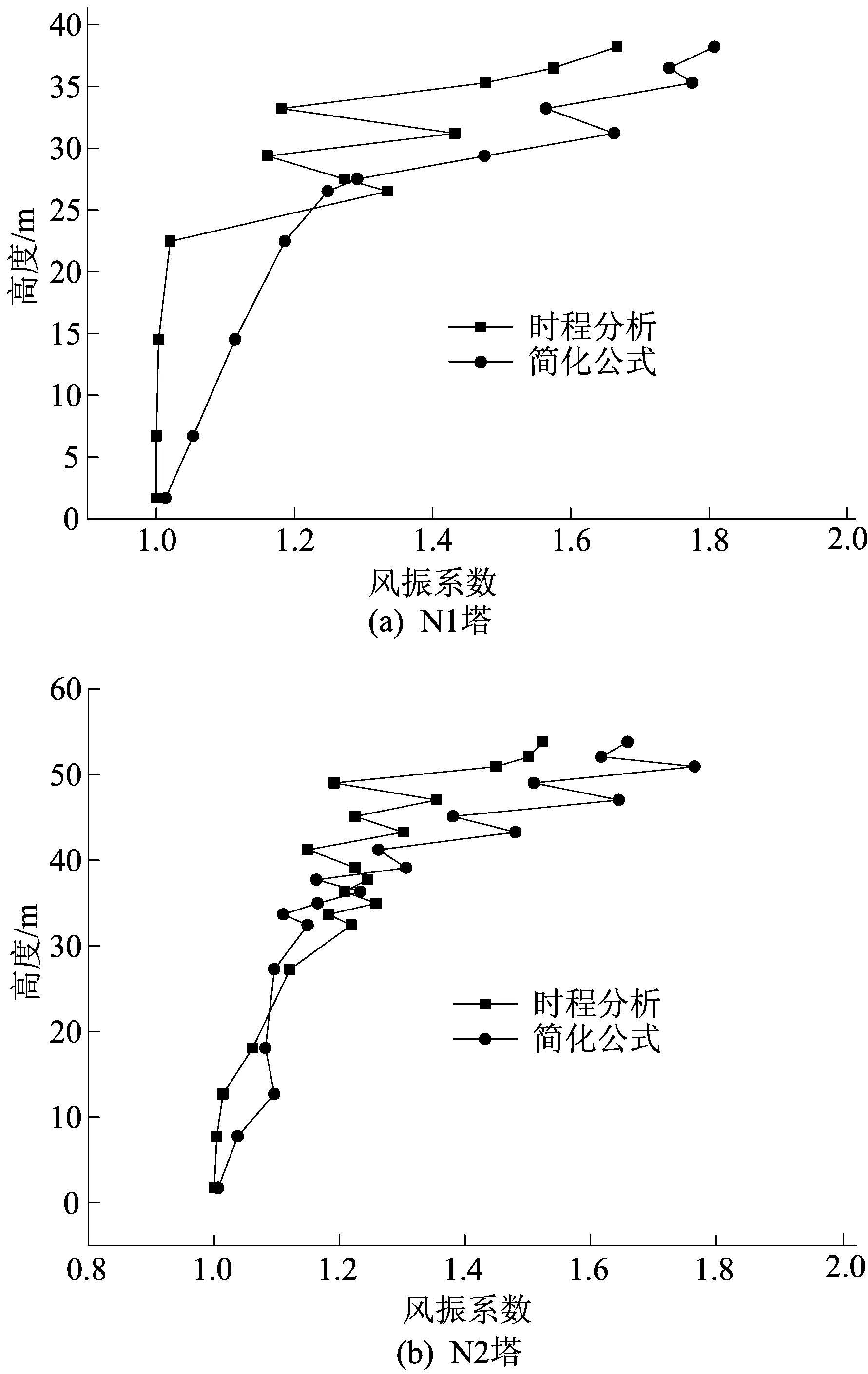
图8 耐张塔简化计算公式与时程分析风振系数结果对比

由图7、图8可知,本文建立的简化计算公式的结果与时程分析所得计算结果吻合度较高,能较好地反映出塔身截面变化对风振系数的影响,同时也具有一定的安全余度,可满足实际工程窄基塔设计分析的需要。

4 结 论

本文针对窄基角钢塔结构设计时的风振系数取值进行了研究,基于谐波合成法对窄基角钢塔进行了动力时程分析,对计算结果进行了分析与讨论,并建立了窄基角钢塔风振系数的简化计算公式，得到如下结论:

(1) 窄基角钢塔风振系数的取值与结果高度成正相关,在横担处由于截面形式的变化而产生突变。数值计算结果与现行规范的风振系数取值结果相差较大,规范取值不适用于该类根开较小的新型窄基角钢塔。

(2) 直线型与耐张型窄基塔由于受力形式的不同,风振系数计算值差异较大,在设计时应进行区别处理,分别进行风振系数的取值计算。

(3) 文中通过数据拟合所建立的不同类型窄基角钢塔风振系数简化计算公式与时程分析的计算结果吻合度较高,能较好地反映出塔段截面变化对风振系数造成的影响,且有一定的安全余度,因此该简化计算公式可满足窄基角钢塔的设计需要。