基于工况识别的PHEB能量管理策略研究
2020-03-23尹安东张黎明
尹安东, 张黎明
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
插电式混合动力客车(plug-in hybrid electric bus,PHEB)具有纯电行驶能力,且续航里程不受限制,是传统燃油客车向纯电动客车过渡的一种方案。PHEB具有内燃机和动力电池2个动力源,良好的能量管理策略能够实现需求功率在不同动力源之间的合理分配和动力系统各部件之间的协调控制,从而达到节能减排的目的。能量管理策略作为PHEB的核心技术之一,对整车的动力性、经济性和排放性具有重要影响[1]。
目前对PHEB能量管理策略可分为基于规则的控制策略和基于优化的控制策略两大类[2]。基于规则的控制策略,文献[3]根据不同荷电状态(state of charge,SOC)范围将PHEB的工作模式分为3种,每种工作模式对应不同的控制规则,通过不同工作模式的组合以减少燃油消耗,但无法保证能耗最优,且规则的制定依赖于设计人员经验;基于优化的控制策略,文献[4]提出了一种将全局优化与瞬时优化算法相结合的控制策略,能实时应用,但要求预先知道行驶工况。文献[5]、文献[6]分别用粒子群优化(particle swarm optimization, PSO)算法、动态规划(dynamic programming,DP)算法对基于规则的控制策略进行优化以降低等效燃油消耗量,但没有考虑行驶工况的影响。
本文提出一种基于工况识别的能量管理策略。首先针对合肥市混合交通的特点运用主成分分析(principal component analysis,PCA)和模糊C均值聚类法构建代表性行驶工况;然后基于学习向量量化(learning vector quantization,LVQ)神经网络进行工况识别,根据识别结果确定工作模式,并利用改进的DP算法进行PHEB能量管理控制优化;最后以某款PHEB为研究对象进行仿真验证。
1 代表性城市工况的构建
1.1 短行程及其特征参数获取
汽车的行驶工况可用速度-时间历程描述,可为整车动力系统参数匹配、控制规则制定和能量消耗检测提供参考依据。选取经过胜利路等5条代表性路线的10条公交运行线路,借助OSE-Ⅱ速度传感器和AM-2006S汽车性能综合测试仪等试验设备,连续两周对选取的公交线路进行行驶数据采集和处理,提取出392组短行程。为准确描述每个短行程,根据文献[7-9]选取14个特征参数,见表1所列。

表1 短行程特征参数
1.2 短行程的主成分分析
PCA是把多个变量转为少数互不相关的综合变量(主成分)的过程,这些主成分通常为原始变量的线性组合,能反映原始数据的大部分信息。具体分析步骤如下:
(1) 构建短行程样本观测矩阵X,其中xi,j表示第i(i=1,2,…,392)个短行程对应的的第j(j=1,2,…,14)个特征参数的值。
(2) 为避免特征参数单位差异带来的影响,对观测矩阵X进行标准化处理,使得每列的均值为0,标准差为1,得到标准化矩阵Y,即
(1)
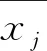
(3) 计算标准化矩阵Y相关系数矩阵R,即
(2)
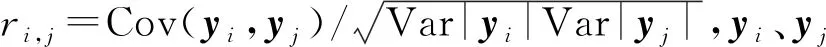
(4) 求解主成分,需要进行变换,即
(3)
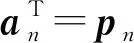
(5) 提取主成分。第n个主成分fn的方差与所有主成分方差和的比值称为该主成分的贡献率,表示该主成分所包含原始信息的多少,前j个主成分的贡献率之和称为前j个主成分的累计贡献率(按方差从大到小排列),通常取累计贡献率超过80%的主成分来代替原始变量。主成分的方差和贡献率见表2所列。由表2可知,前3个方差大于1的主成分累计贡献率为83.165%,可以很好地替代原先的14个特征参数进行分析。
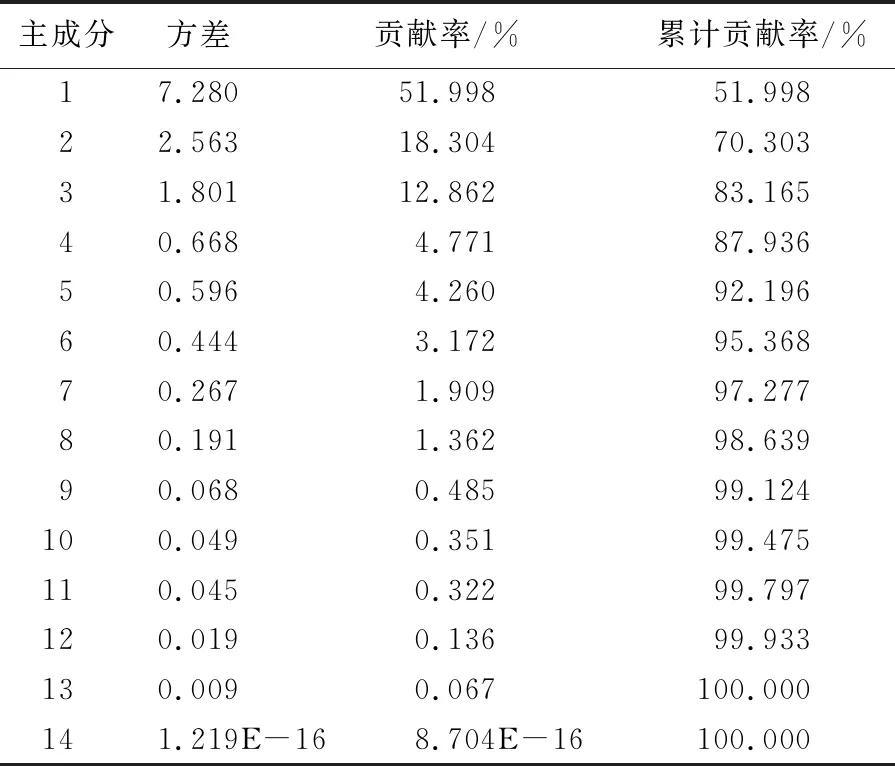
表2 主成分的方差和贡献率
1.3 模糊C均值聚类分析
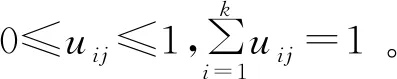
(4)
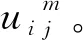
(1) 确定分类个数n,幂指数m>1和初始隶属度矩阵U(0)=(uij(0)),通常取[0,1]上的随机数来确定,令U(h)表示第h步迭代的隶属度矩阵。
(2) 计算第h步的聚类中心C(h),即
(5)
其中,i=1,2,…,k;j=1,2,…,n。
(3) 修正隶属度矩阵U(h),计算第h步的目标函数J(h),即
(6)
(7)
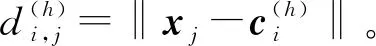
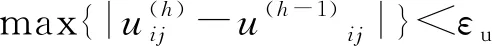
经上述步骤迭代对主成分得分矩阵的前3列进行聚类,可以求得最终的聚类中心C和隶属度矩阵U。将短行程数据分为3类,按时间比例挑选出距离聚类中心最近的短行程构建代表性城市工况,如图1所示。将构建的代表性工况的部分特征参数与总的实验数据的特征参数比较验证,误差均小于10%,且误差均值为4.86%,构建的代表性工况能较好地反映原始数据的信息。

图1 合肥市代表性城市工况
2 LVQ神经网络工况识别
LVQ神经网络能够对复杂和非线性的对象进行高效识别,结合监督学习与竞争学习算法,由输入层、竞争层和线性输出层3层构成[10]。LVQ神经网络结构如图2所示。

图2 LVQ神经网络结构
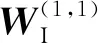
结合PCA结果,取vmin、vmr、da、Pi作为神经网络的输入,50 s为识别周期[11-12],竞争层通过选择最佳神经元和对权系数矩阵进行自适应更新对输入向量进行分类,线性输出层3个神经元代表3种不同的道路工况,识别结果如图3所示。
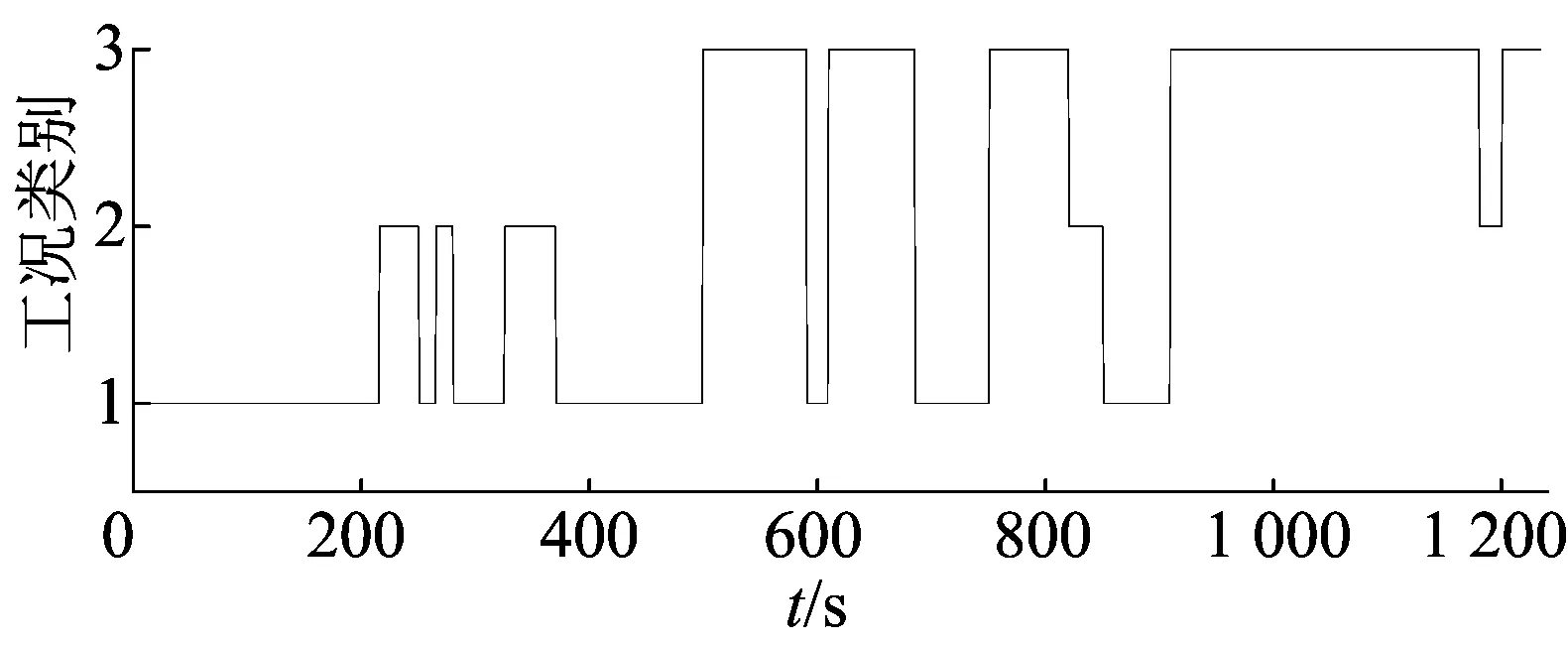
图3 工况识别结果
3 基于工况识别的能量管理策略
3.1 PHEB结构与基本参数
以某款双轴并联式PHEB为研究对象,其发动机和电机输出的动力通过转矩耦合器后输入变速机构,通过后桥进行驱动。整车及主要部件基本参数见表3所列。
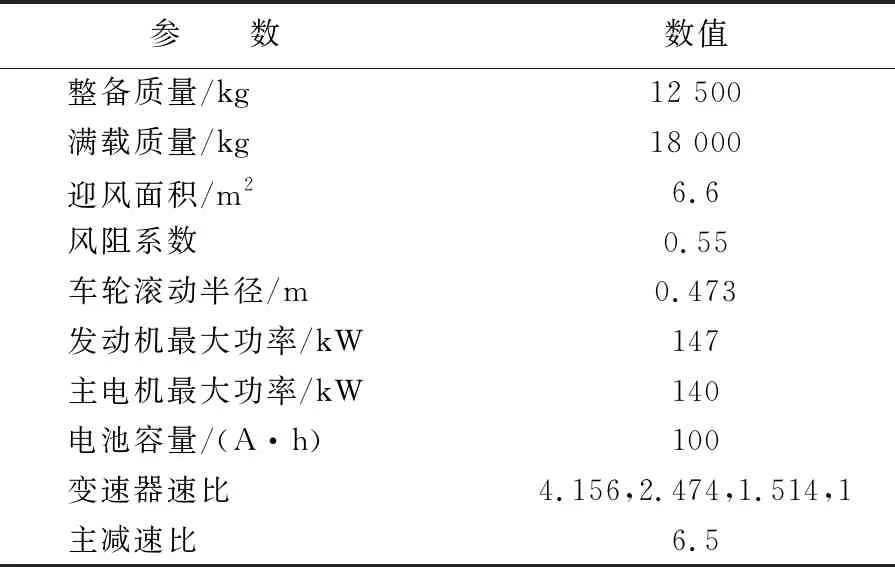
表3 PHEB整车及主要部件参数
3.2 PHEB能量管理策略制定
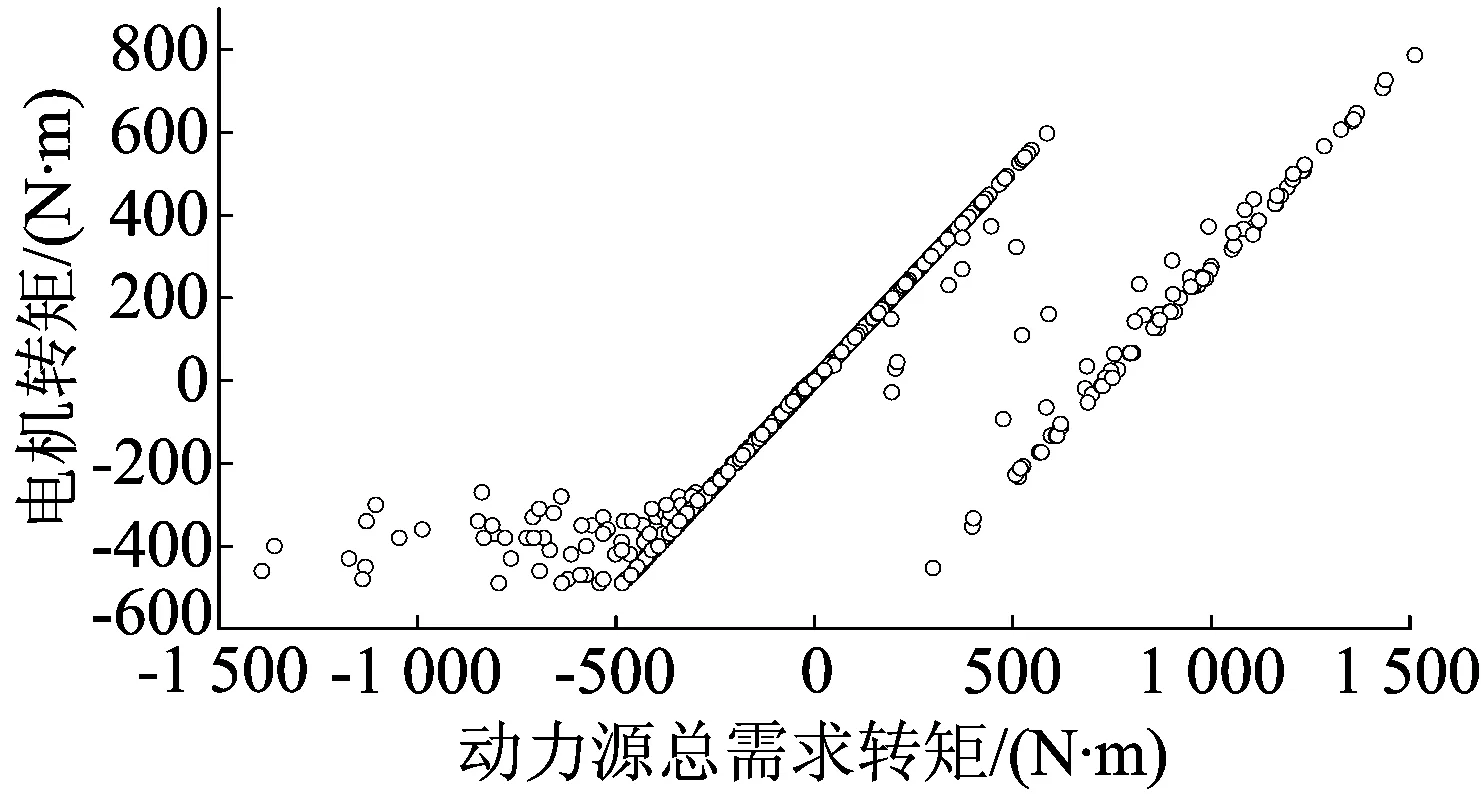
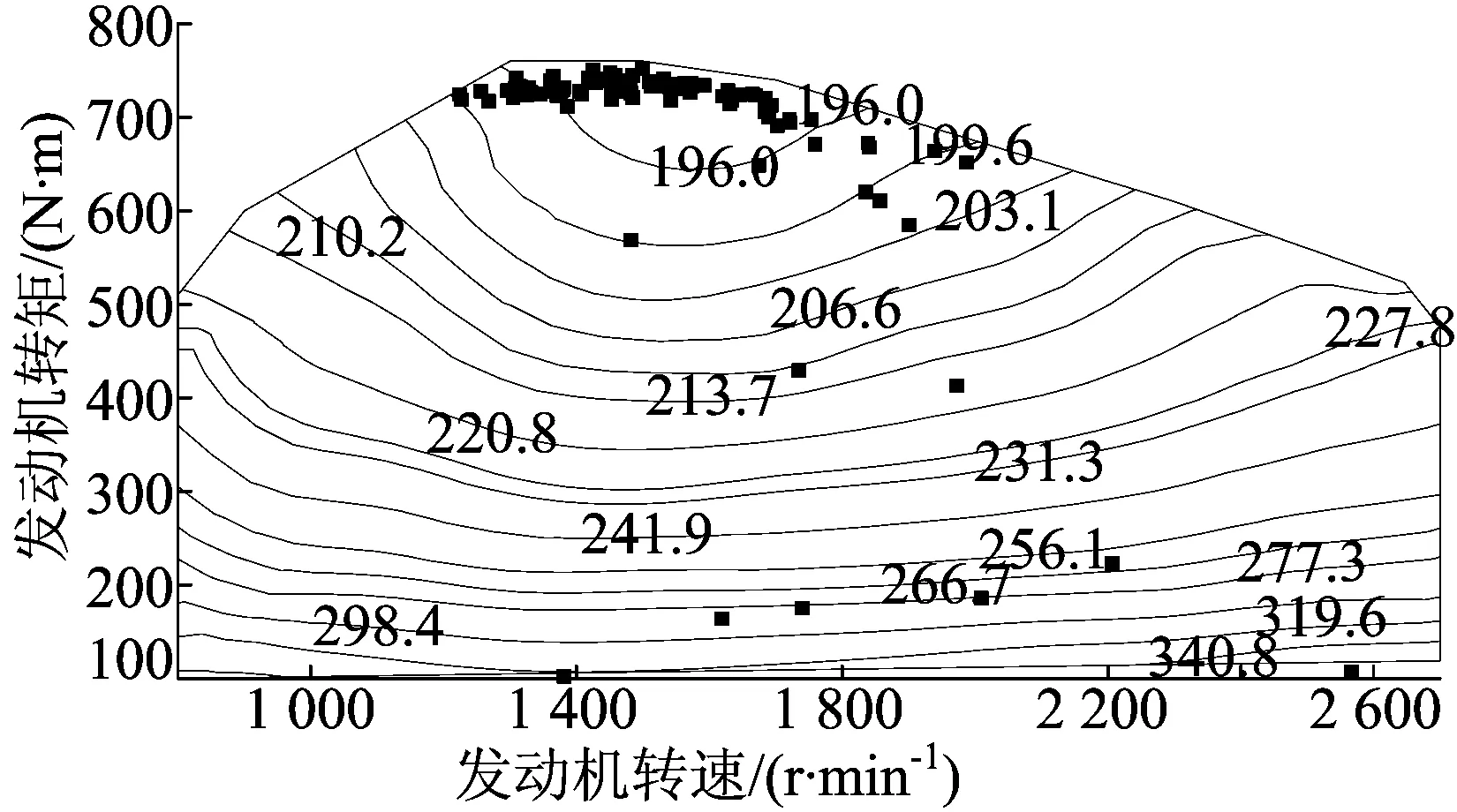
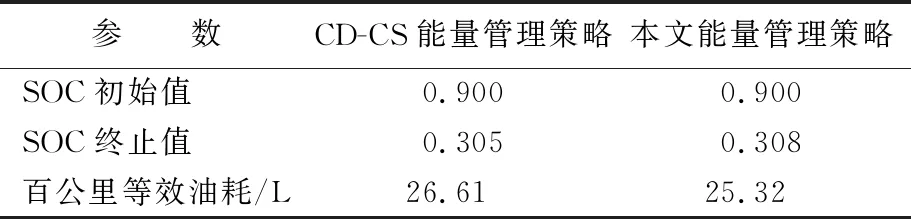
PHEB配备大容量电池,电机可以单独驱动车辆,因此可结合工况识别结果与SOC值确定整车动力系统所处的工作模式,制定能量管理策略如图4所示。工作模式有:① 纯电动(electric vehicle, EV)模式。此时SOC>0.8,整车需求功率由蓄电池供给电机单独提供,由于SOC较高且充电效率低,为保护电池,不进行能量回收。② 电量消耗(charge depletion, CD)模式。此时0.3 图4 基于工况识别的能量管理策略 鉴于PHEB在每个工作模式下所采用的能量管理策略是逻辑门限值控制策略,无法保证能耗最优,因此本文采用 DP算法求得离线全局最优解,提炼出全局最优能量分配规则,对逻辑门限值控制策略进行优化,以取得更好的燃油经济性。 DP算法是将多阶段决策问题转化为一系列单阶段问题逐个求解的最优化控制方法[13-14]。若行驶工况已知,车轮所需转矩Tw由电机输出转矩Tm和发动机输出转矩Te通过动力耦合机构联合提供。三者的转矩、转速关系为: Tw=ηTR(i)(Te+ρTm) (8) (9) 其中,ηT为传动系总效率;ρ为电机与发动机速比;R(i)为第i挡与主减速器的速比乘积;ωe、ωm、ωw分别为发动机、电机、车轮转速。 将构建的工况以1 s为间隔分为N个阶段,以电机转矩Tm、挡位ig为系统控制变量u(K),蓄电池荷电状态SOC为系统状态变量x(K),并对Tm、SOC离散化,得状态传递函数为: (10) 其中,I(K+1)为第K+1阶段的电池电流;η为充放电效率。同时,蓄电池SOC、发动机和电机的转速、转矩需满足下列约束条件: SOCmin≤SOC(K)≤SOCmax, ωe-min≤ωe(K)≤ωe-max, Te-min(ωe)≤Te(K)≤Te-max(ωe), ωm-min≤ωm(K)≤ωm-max, Tm-min(ωm)≤Tm(K)≤Tm-max(ωm) (11) 定义阶段代价函数VK为燃油消耗量Qfuel(K),第K阶段的目标函数JK,N定义为从第K阶段到第N阶段的代价函数之和,即 (12) 则最优目标函数fK为目标函数JK,N的最小值。 离散动态规划由多层循环嵌套构成,其计算负担与问题时间呈线性关系,与状态变量和控制变量离散点成指数关系[15]。PHEB能量管理策略的制定要充分利用电能,SOC变化范围较大,导致计算时间较长。因DP算法的SOC初始值已知,但终止值需要通过正向搜索求得,在20个代表性城市工况循环下,可将一个工况求解得到的终止SOC值作为下一个工况的初始SOC进行运算,并根据终止SOC值调整下一循环工况的SOC变化范围。设该行驶工况循环n次,则第m个循环的SOC变化区间大小为: (13) SOCm-ΔSOCm≤ΔSOCm′≤SOCm (14) 通过改进后的DP算法求得需求转矩与电机转矩关系、发动机工作点分布分别如图5、图6所示。 由图5可以得出动力源总需求转矩Treq与电机输出转矩Tm、发动机输出转矩Te的关系为: (15) 由图6可以看出,发动机工作点大部分处于燃油消耗率低的区间。 图5 动力源总需求转矩与电机输出转矩关系 图6 改进DP算法中发动机工作点分布 基于AMESim和Simulink软件分别建立整车物理模型和能量管理策略,如图7所示。 根据DP算法对原有能量管理控制规则进行改进,取蓄电池初始SOC值为0.9,目标终止值为0.3,在20个代表性城市工况循环下,分别对本文能量管理策略和CD-CS控制策略进行仿真比较。两者的SOC变化、发动机工作点分布情况分别如图8、图9所示,等效油耗见表4所列。 图7 PHEB整车与能量管理策略 图8 SOC变化曲线 图9 发动机工作点分布 表4百公里燃油经济性比较 参 数CD-CS能量管理策略本文能量管理策略 SOC初始值0.9000.900SOC终止值0.3050.308百公里等效油耗/L26.6125.32 由图8可知,本文基于工况识别的能量管理策略SOC降低速度较慢,直到运行至第14个循环工况时才降到0.3附近,之后一直处于电量维持阶段;而CD-CS控制策略运行至第6个循环工况时SOC值就降低到0.3附近,之后处于电量维持阶段。由图9可知,本文能量管理策略将发动机工作点更加集中在低燃油消耗率区域。由表4可知,2种能量管理策略虽然都能充分利用电池电能,但本文能量管理策略能够根据工况识别的结果匹配相应的工作模式,其等效百公里燃油经济性[16]比CD-CS能量管理策略提升了5.2%。 本文针对合肥市混合交通的特点,基于PCA和模糊C均值聚类法构建出代表性城市行驶工况;利用LVQ神经网络进行工况识别,根据识别结果确定整车能量管理工作模式;基于DP算法进行能量管理策略优化;最后在AMESim和Simulink联合仿真平台上基于实例进行了仿真验证。仿真结果表明,与CD-CS控制策略相比,本文提出的基于工况识别的能量管理策略燃油经济性有较大提升。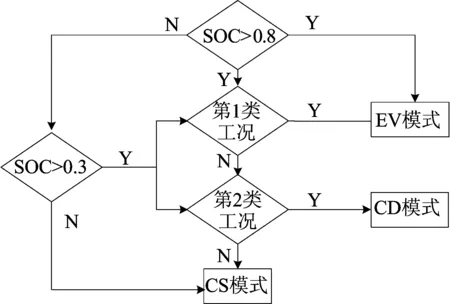
4 基于DP算法的控制策略优化
4.1 DP算法
4.2 DP算法改进
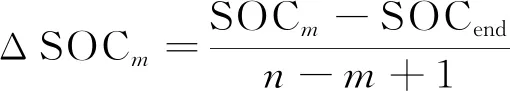

5 仿真结果与分析



6 结 论
