12 bit 100 MS/s Flash-SAR混合型模数转换器的设计与实现

张 章, 吴 宵, 解光军

(合肥工业大学 电子科学与应用物理学院,安徽 合肥 230601)

随着集成电路互补金属氧化物半导体(complementary metal-oxide-semiconductor, CMOS)工艺的快速发展,逐次逼近型模数转换器(successive approximation register analog-to-digital converter,SAR ADC)运用了较多的数字模块,从而能更受益于半导体工艺发展所带来的进步。SAR ADC因其结构简单、面积较小、功耗较低等优点受到广泛的研究和运用。传统结构的NbitSAR ADC[1]完成1次转换需要进行N次比较,每次比较又受到电容型数模转换器(digital-to-analog converter,DAC)的时间建立和逻辑控制电路传输延时的限制,因此传统结构的缺点限制了SAR ADC 向高速、高精度发展的趋势。对于以SAR ADC为基础的高性能混合型ADC,已经有一些研究成果,如文献[2]提出的 Pipeline-SAR 混合型ADC、文献[3]提出的基于SAR结构的时间交织ADC、文献[4]提出的Flash-SAR 混合型ADC。其中,Pipeline-SAR 混合型 ADC 能有效提高传统 SAR ADC 的速度,但是流水线(pipeline)ADC中的高性能运算放大器的设计使系统趋于复杂化,不能达到低功耗的要求;时间交织型 SAR ADC 虽然有效提升了整个电路系统的速度,但通道间存在的时间失调严重影响ADC的整体性能,需要设计相应的校准电路来校准误差,额外增添了功耗;快闪型-逐次逼近混合型模数转换器(flash successive approximation register analog-to-digital converter,Flash-SAR ADC)是一种集Flash ADC[5]和SAR ADC两者优点的新型结构ADC,可以使ADC整体速度、面积、功耗以及精度等性能达到更好的折中,因而得到广泛的研究。

1 Flash-SAR ADC的结构和工作原理

1.1 Flash-SAR ADC 电路结构

传统型SAR ADC只有当电容阵列DAC上的电压建立达到要求时,才能触发比较器进行比较。在电容阵列DAC中高位电容大小是剩余低位电容值的总和,因此在转换过程中建立时间最长。为了减少转换过程中的时间,可以将Flash-SAR ADC中高位的几个电容进行并行转换,从而减少转换时间。

本文设计的Flash-SAR 混合型ADC的电路架构如图1所示,其结构主要包括第1级Flash ADC、第2级SAR ADC以及相应的数字校准电路。

图1中,DEC表示开关切换控制;B1～B11表示切换开关;D0～D11表示不同电容值的电容；CLK1表示控制Flash ADC进行粗量化的时钟信号;CLK2表示控制SAR ADC进行细量化的时钟信号。

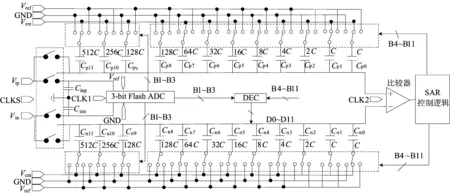
图1 Flash-SAR ADC的电路结构图

第1级Flash ADC包含3 bit Flash以及数字编码电路。其中，Vip为差分正相模拟输入电压；Vin为差分反相模拟输入电压；CLKS表示采样时钟信号；Vref为参考电压；GND表示连接地信号；Vcm为共模输入电压。

第2级SAR ADC包含DAC电容阵列,高、低位底极板电容电平切换控制模块以及实现比较功能的比较器,其中电容阵列中C表示单位电容值,其他电容值依次是单位电容的偶数倍。

该混合型ADC在开始阶段,利用Flash ADC并行快速转换的优点对输入的前3 bit信号进行粗量化,并得到前3 bit对应的数字输出码;然后使用第2级的SAR ADC对余下的10 bit进行细量化处理,最后求出整个混合型ADC的12 bit数字输出码。

传统结构SAR ADC与Flash-SAR混合型ADC的流程对比如图2所示。图2中,1st、2nd、3rd、4th、5th分别表示第1级～第5级;Comp表示比较器;Set表示复位信号,低电平有效。从图2可以看出,Flash-SAR混合型ADC可以减少SAR在1个转换周期内原来需要多次进行转换的次数,因此SAR ADC的转换速率得到了有效提高。在电路设计中通过加入1 bit冗余位可以校准出一定的失调电压,因此当第1级Flash ADC中比较器的失调电压低于这个失调电压的限度,第2级中的数字校正电路都可以对出现误差的结果进行校准,不会对ADC的整体性能造成影响。

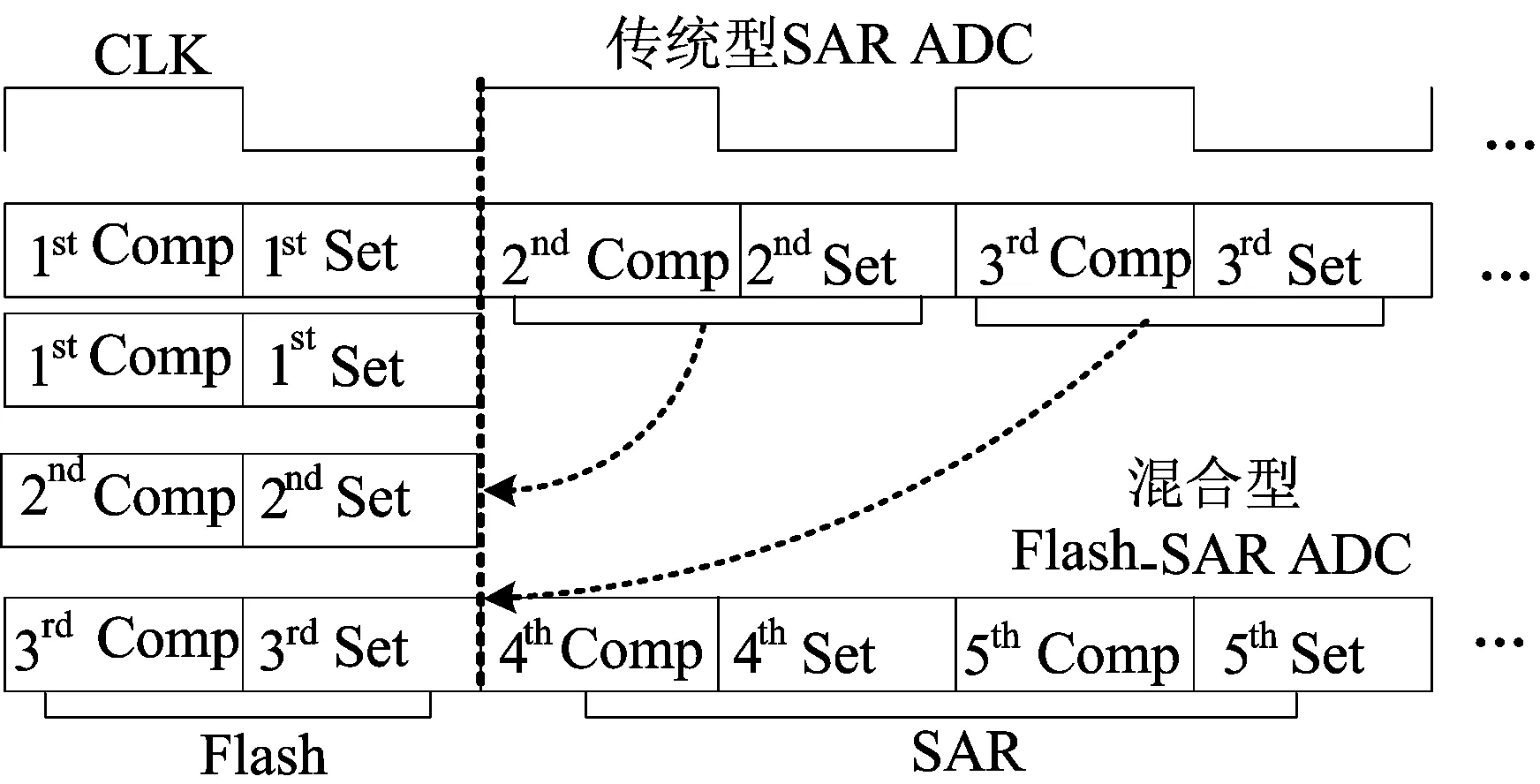
图2 传统SAR ADC与Flash-SAR混合型ADC流程对比

1.2 Flash-SAR ADC 工作原理

Flash-SAR ADC时序如图3所示。

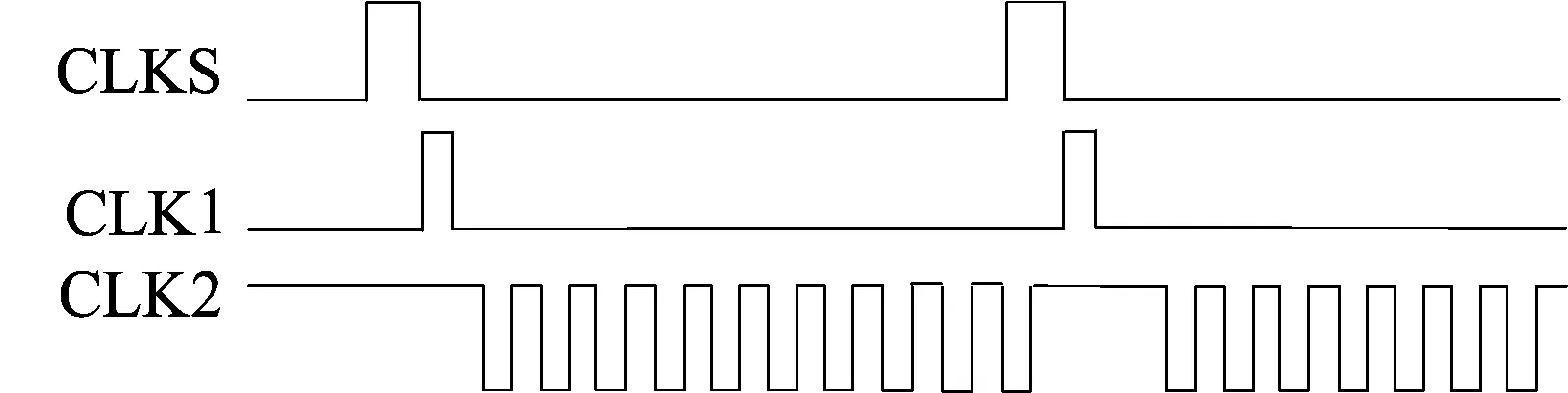
图3 Flash-SAR ADC 时序图

(1) 当CLKS置于高电平,Flash ADC、SAR ADC同步采样输入的模拟信号,采样后的信号在采样电容顶极板上以电荷量的形式储存。

(2) 当第1阶段采样结束时,采样时钟CLKS变为低电平,这时粗量化控制时钟CLK1置于高电平,然后对存储在Flash ADC顶极板上的电压作粗量化处理，量化处理后的数字输出码再利用高位电容跳过与复用(higher capacitor skipped or reused,HCSR)[6]算法控制电容阵列底极板的切换方式。粗量化处理完成后,CLK1、CLK2分别被置于低电平、高电平,这时SAR ADC对保存在顶极板上的电压作细量化处理。

(3) 细量化处理完成后,再根据所得的数字码通过HCSR算法控制下一位电容阵列底极板的电平切换。

2 电容阵列DAC单位电容的选取

在电路设计时,为使ADC的精度不受采样电路热噪声的影响,ADC的量化噪声必须远大于采样电路总的热噪声。Nbit ADC的量化噪声可表示为:

(1)

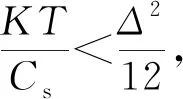
(2)

其中,Δ为ADC理想步长,大小为1LSB;Cs为单位采样电容;K为玻尔兹曼常数;T为温度;VFS为ADC输入信号幅值。LSB表示最低有效位(least significant bit)。

针对本文设计的12 bit 100 MS/s混合型ADC,将相应参数代入(2)式,当VFS=1.75 V时,计算求出Cs至少为27 fF。

在12 bit的SAR ADC中,Cs相对来说电容值比较小,其原因是电容阵列型DAC的总电容值很大,因此对于中等精度SAR ADC,限制单位电容值大小的主要影响因素不是噪声而是电容的失配[7]。

本文中,因为SAR ADC在进行细量化时对电容的匹配度要求严格,所以电路设计过程主要考虑SAR ADC中电容失配的问题并给出分析,最后求出单位电容值。具体的推导如下:

假设C1=Cu+ε1,Ci=2i-2Cu+εi(i=2,3,…,N-1),其中εi为第i位理想(ideal)与实际(real)电容值的差值;Cu为DAC中单位电容。若电容之间均满足正态分布,则第i位电容的方差为:

(3)

其中,i=2,3,…,N-1;σu为Cu的标准差。设SAR ADC的输入信号为Y,其大小为:

(4)

其中,bi为0、1/2、1各项对应代表DAC电容阵列底极板的GND、Vref、Vcm。

Nbit电容型DAC的模拟输出为:

(5)

SAR ADC中积分非线性(integral nonlinearity,INL)和差分非线性(differential nonlinearity,DNL)的计算公式分别为:

(6)

DNL(Y)=INL(Y)-INL(Y-1)

(7)

将 (7) 式带入(6) 式可得:

(8)

(9)

当在满量的1/2时INL(Y)取得最大值,即Y=2N-1,通过(9) 式求得方差为:

INLmax=INL(2N-1)=

(10)

则得到σINL的表达式为:

(11)

在实际运用时达到好的良率需要满足如下条件:

3σINL<0.5LSB

(12)

通过电路的工艺说明,能够查阅到σu和电容值的失配系数AC,两者关系式为:

(13)

联立(11)～(13) 式可求得在线性度[8]要求下,电容阵列Cu的最小值为:

(14)

3 HCSR开关策略

本文采用HCSR开关策略,通过Flash ADC作粗量化处理所得到的量化结果决定SAR ADC中电容阵列的工作方式。通过对合并电容开关(merged capacitor switching,MCS)[7]策略进行改进,把连接在恒定Vcm端的电容也采用开关切换,从而对LSB进行判断。与文献[7]MCS开关切换策略相比,本文采用的开关策略在电容阵列中使用的电容数量减少了1/2,使整个电路的功耗和面积大大降低。

HCSR算法原理如图4所示。图4中,C6=C5=2C,C4=C3=C2=C1=C。

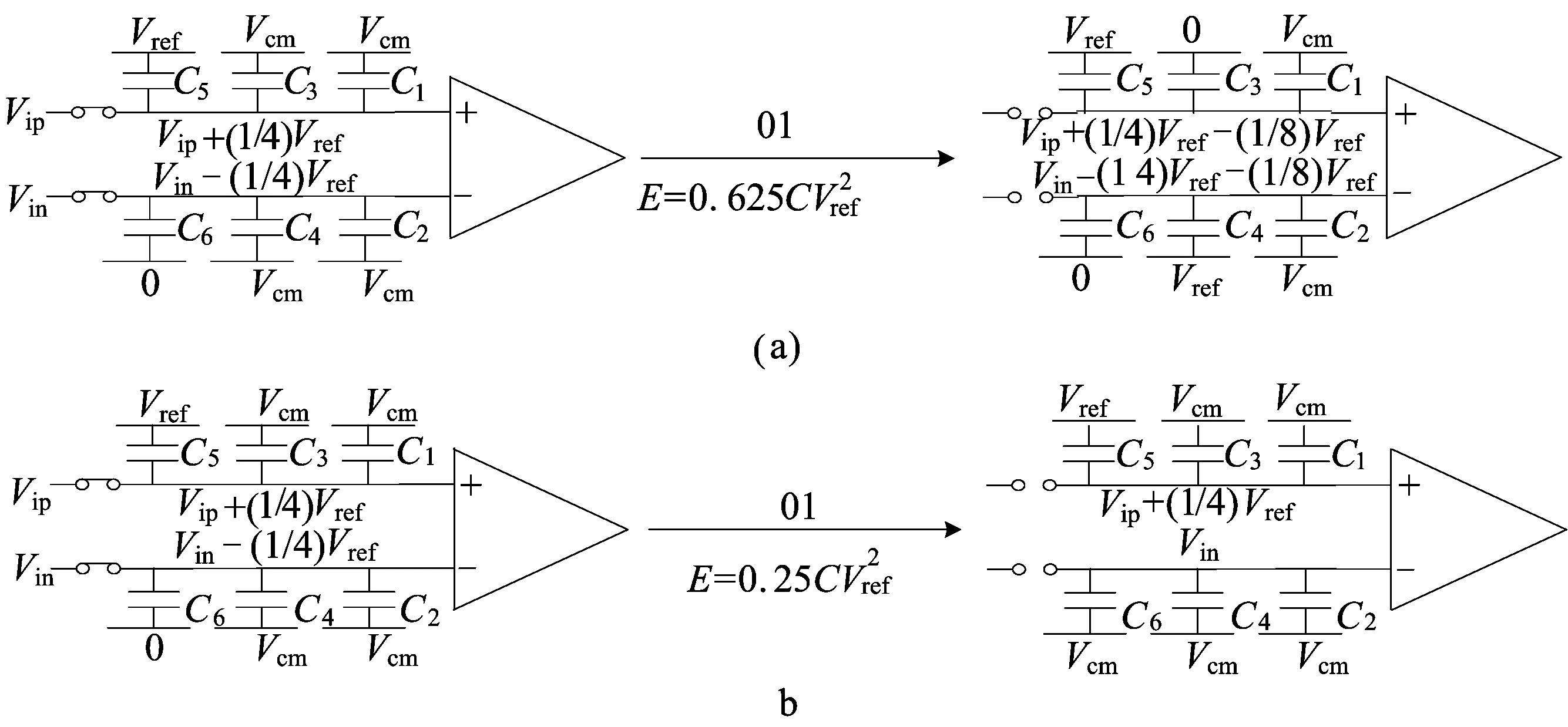
图4 HCSR算法原理

开关切换功耗如图5所示。图5中,Csw为切换开关后充电达到Vref时的电容;Cnsw为开关未切换保持状态不变时的电容;CT为电容阵列的总电容。

从图5可以看出电容进行充放电的过程,其采用传统二进制的搜索方式。当开关进行切换,Csw的底极板从GND充电到Vref后所消耗的能量为:

(15)

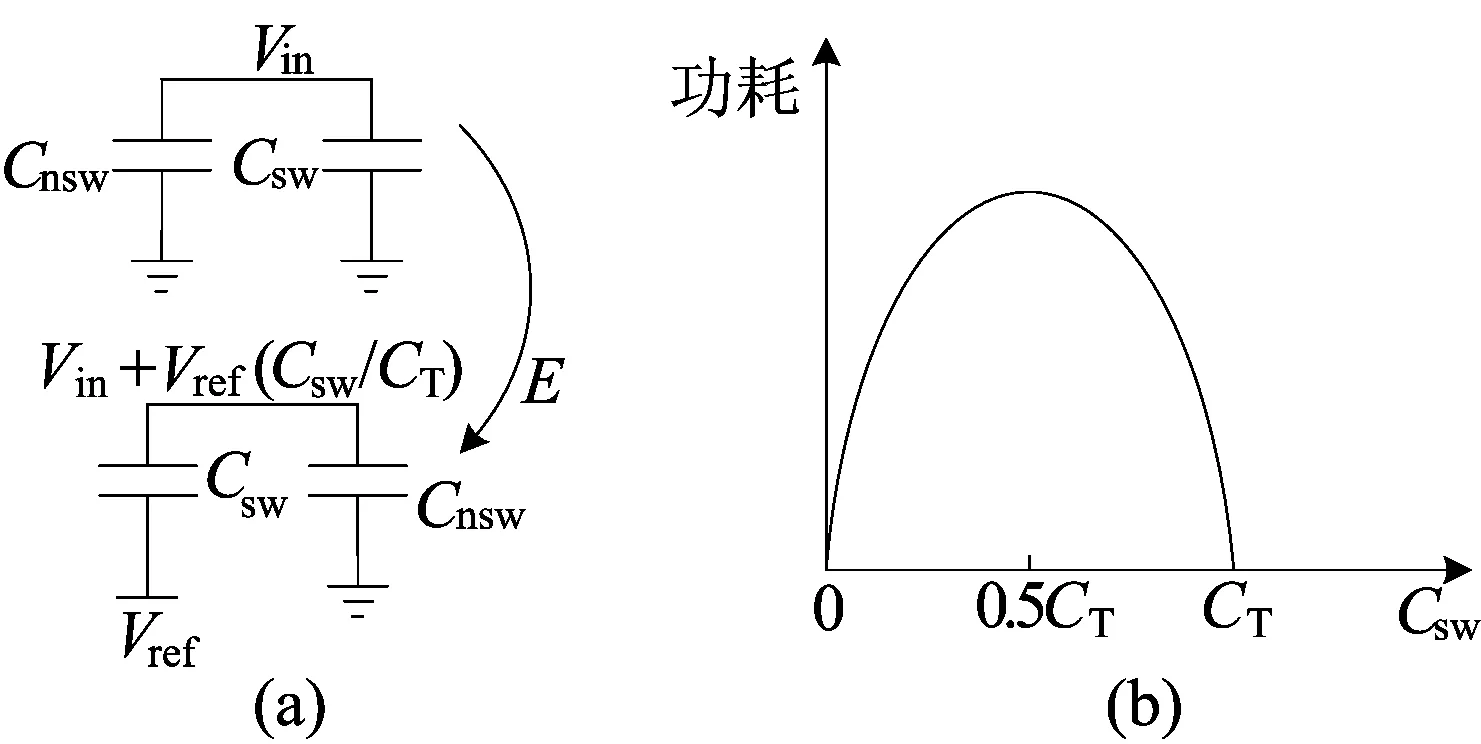
图5 开关切换功耗

在上述传统型开关切换中每个电容都需要进行充放电,这样会增大能量消耗,ADC不能实现低功耗。本文设计的 ADC,电容阵列不需要每次都对高位电容充放电。这是由于Flash ADC中已经对采样的输入信号高几位通过并行的方式进行了粗量化,最后根据粗量化的结果判断采样差分信号差值的大小关系:若两者之差较大,则电容阵列对电荷重分配时要对高位电容充放电;若得到的差值较小,则高位电容不需要进行充放电,保持原来状态即可。

4 SAR ADC带冗余位校准算法

基准参考电压可以量化为相应位的输出码,不带冗余位的二进制搜索算法如图6所示。

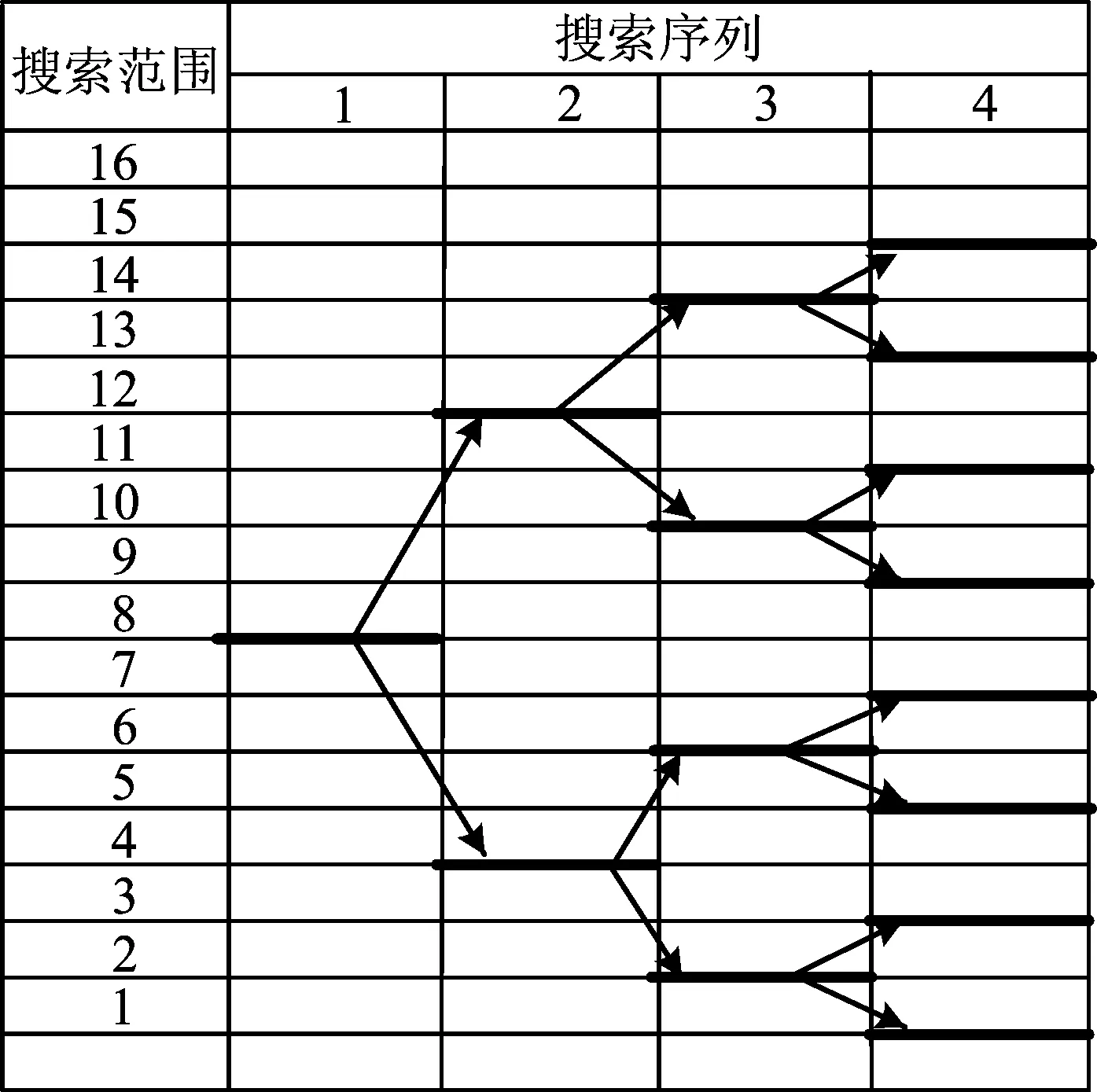
图6 不带冗余位的二进制搜索算法

采用二进制搜索算法[9]的SAR ADC,在比较过程中,如果比较器的判断出现错误,那么会影响正确数字码的输出。图6中给出了对应数字码的搜索范围和序列。由图6可知,在每个转换周期过程中二进制搜索范围是彼此独立、不会产生任何交叠的,若在搜索过程中某个搜索被遗漏,则此次量化环节不会再出现。由于传统二进制搜索算法没有出现重叠的现象,某位数字码出现误判断时,不能被校准正确,因此其不具备纠错功能。

若同一转换周期中搜索范围出现重叠现象,可能被漏搜索的范围能够被重新查找,则可以重新生成正确的数字输出码。为了出现重叠的搜索范围,整个ADC转换的周期至少要比原来多2个子ADC的转换周期,虽然多几个周期,但该算法拥有强大的纠错能力,并增强了整个电路系统的鲁棒性。下面通过实例进行说明。

例1 4 bit 4-step ADC。采用传统二进制搜索算法的搜索范围和序列如图7所示。由图7可知,仅需要4个时钟周期就可以得到完整的数字码,其中S=[8,4,2,1]称作8421码编码方式，是一种二进制转化为十进制的编码方法；S(j)(j=1,2,3,4)表示对应期的数字码。

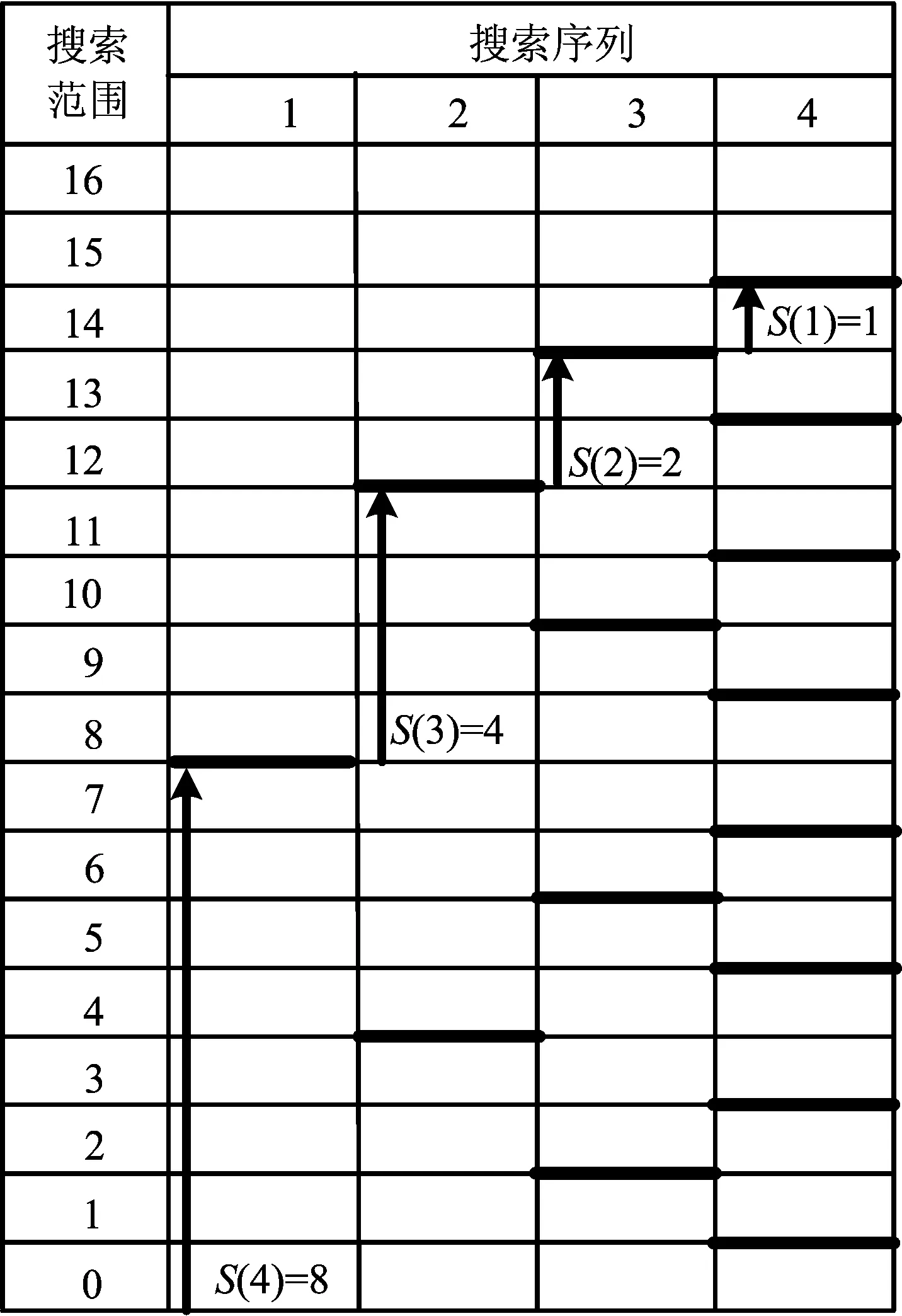
图7 4 bit 4-step ADC采用传统二进制搜索算法搜索情形

例2 4 bit 6-step ADC。采用子二进制搜索算法[9]的搜索范围和序列如图8所示。由图8 可知,要实现与例1相同位数的ADC,需要6个周期进行转换,其中S=[8,2,2,1,1,1]。

在上述2个实例中,S各自相加后的值都为15,该结果证明2种算法都能够完成各位数字码的量化。Nbit ADC经过M次转换的输出码为:

b([0]-1)

(16)

其中,Dout为二进制最后的数字输出;b[j]为第j位的数字输出;M为整个ADC的转换周期。例2结果表明,在原来SAR ADC中额外增加2个冗余位,可有效提高整个ADC的容错性。

例3 4 bit SAR ADC带冗余位的数字误差校准。SAR ADC带冗余位的数字误差校准如图9所示,Error表示出现错误。

图9中,左图为理想的4 bit SAR ADC实例,整个转换过程是完全正确的;中图中,当比较器出现误判时,电路中DAC所产生的基准电压出现错误,并且在第1个转换周期出现错误;右图中,ADC在第2个转换阶段出现错误,由于比较器产生错误的判断,DAC进行开关切换后所分配的基准电压出现错误[10]。

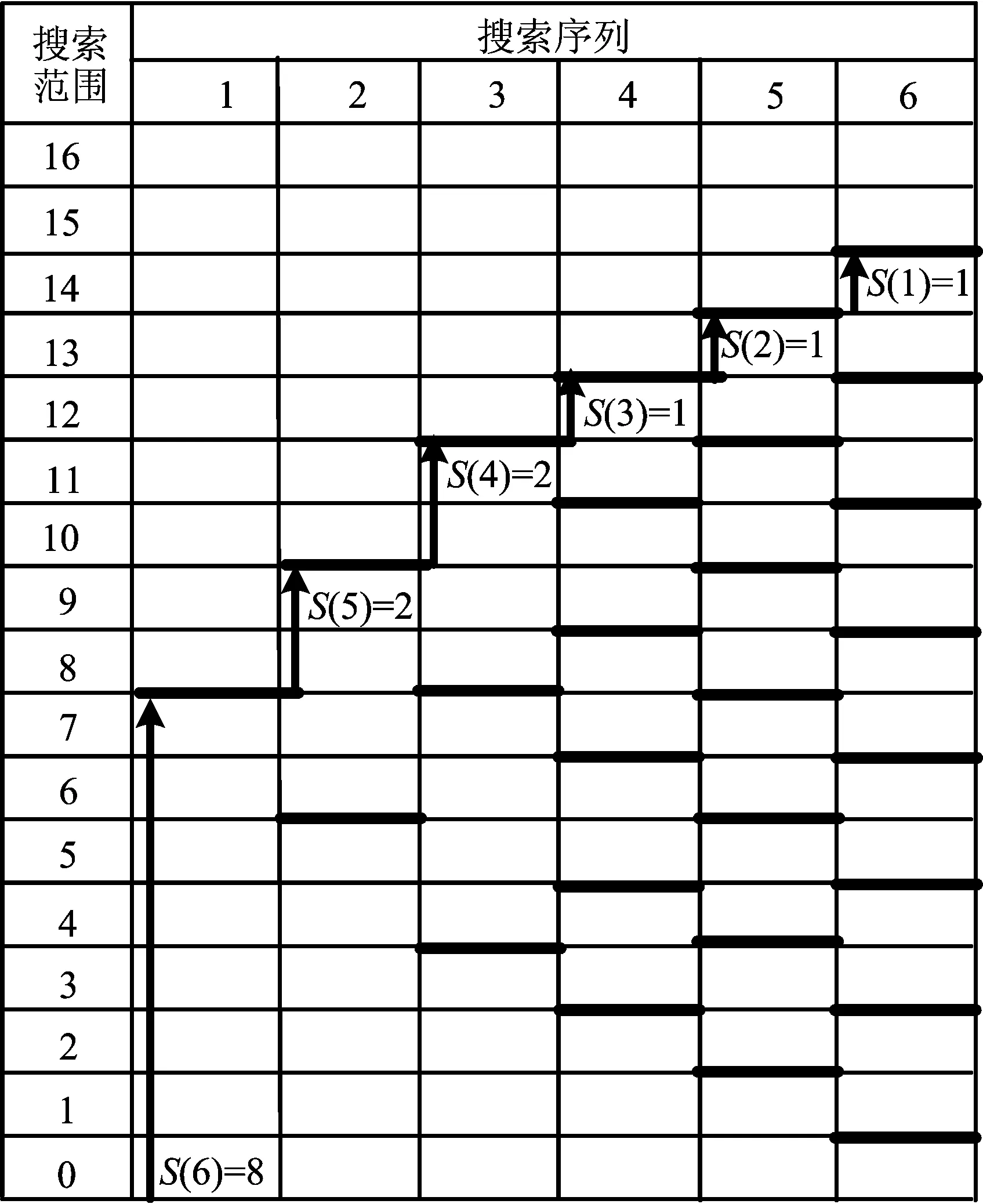
图8 4 bit 6-step ADC采用子二进制搜索算法搜索情形

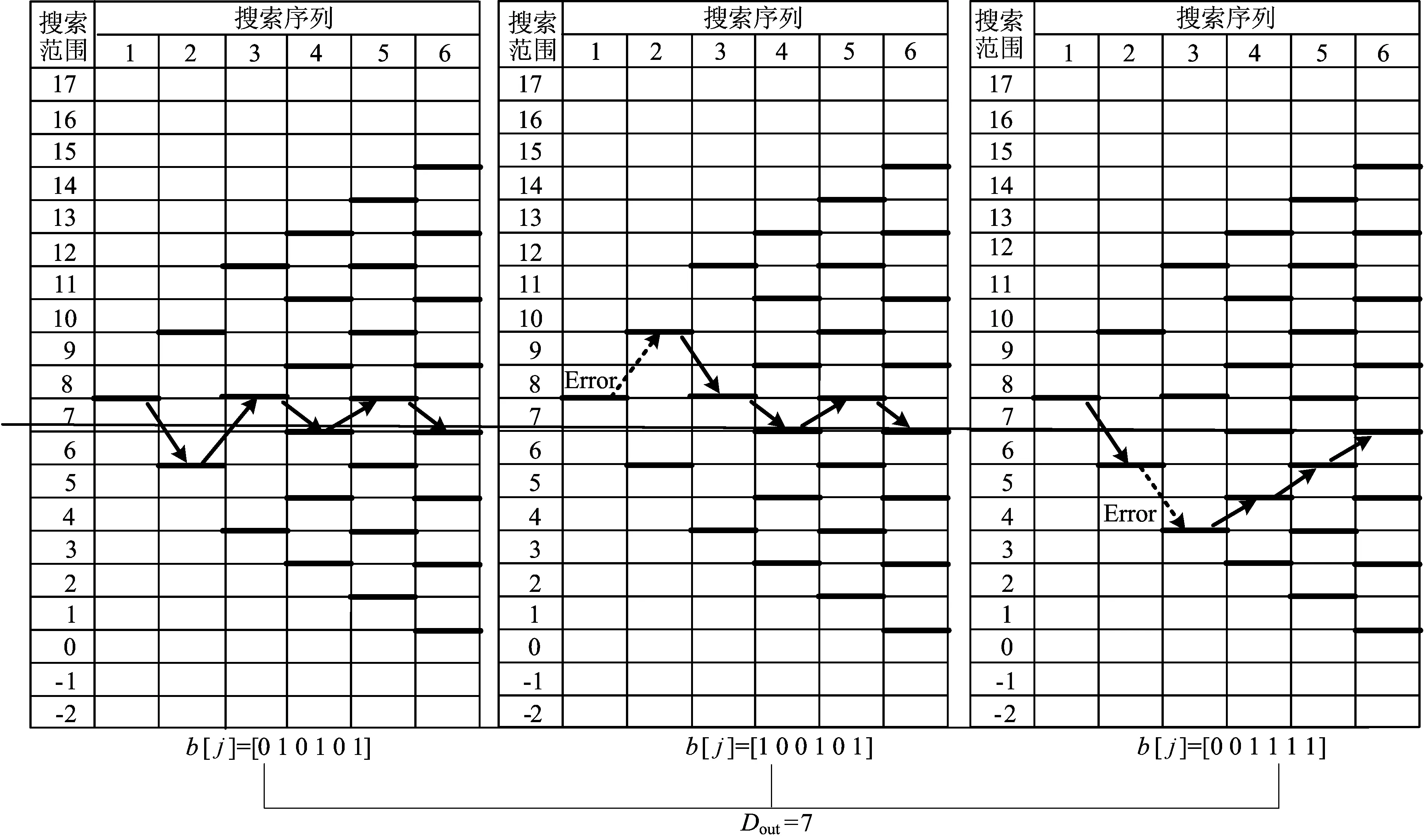
图9 4 bit SAR ADC带冗余位的数字误差校准

当模拟输入信号Vin=7.2 V,采用上述子二进制搜索算法时,得到3个序列为[0,1,0,1,0,1]、[1,0,0,1,0,1]、[0,0,1,1,1,1],3个数字序列对应的十进制数字输出经过(16)式计算后得到相同的Dout=7。3个序列的计算过程如下:

[0,1,0,1,0,1]→8+(2·0-1)×2+

(2·1-1)×2+(2·0-1)×1+

(2·1-1)×1+(2·0-1)×1+

(1-1)=7;

[1,0,0,1,0,1]→8+(2·0-1)×2+

(2·1-1)×2+(2·0-1)×1+

(2·1-1)×1+(2·0-1)×1+

(1-1)=7;

[0,0,1,1,1,1]→8+(2·0-1)×2+

(2·1-1)×2+(2·0-1)×1+

(2·1-1)×1+(2·0-1)×1+

(1-1)=7。

其中,序列[1,0,0,1,0,1]、[0,0,1,1,1,1]是在比较器出现误判断情形下产生的,运用校准算法后,它们的数字输出为Dout=7,和比较器正确运行下输出的结果一样。

上述推导和分析表明,带冗余位的校准算法能够准确地校准转换中出现的错误。

5 电路仿真结果及分析

本文用SMIC 0.18 μm CMOS混合信号工艺设计了一款12 bit 100 MS/s Flash-SAR混合型ADC。所设计的ADC采用“3+10”的2级流水线结构,最后通过冗余位数字校准电路得到12 bit的量化精度。

电路仿真低频时的频谱如图10所示,接近Nyquist高频时的频谱如图11所示,不同输入频率下的SFDR、SNDR变化如图12所示。图10～图12中,SNDR表示信号-失真噪声比(signal-to-noise and distortion ratio);SNR表示信噪比(signal-to-noise ratio);THD表示总谐波失真(total harmonic distortion);SFDR表示无杂散波动态范围(spurious-free dynamic range);ENOB表示有效位(effective number of bits)。

由图10可知,当采样低频时,ADC的ENOB为 11.130,SNR为 68.800 dB,THD为-89.845 dB,SFDR为97.706 dB。由图11可知,当采样频率为100 MHz,输入信号频率为接近Nyquist频率时, ADC的ENOB为 10.990,SNR为 67.973 dB,THD为-87.313 dB,SFDR为95.381 dB。

由图 12可知,在低频输入时, SFDR 较高;而在高频输入时,SFDR 较低;在整个 Nyquist 频率范围内 SNDR的变化相对较小,这是由于不论输入信号的频率大小,限制 ADC 性能的主要因素是量化噪声以及热噪声。

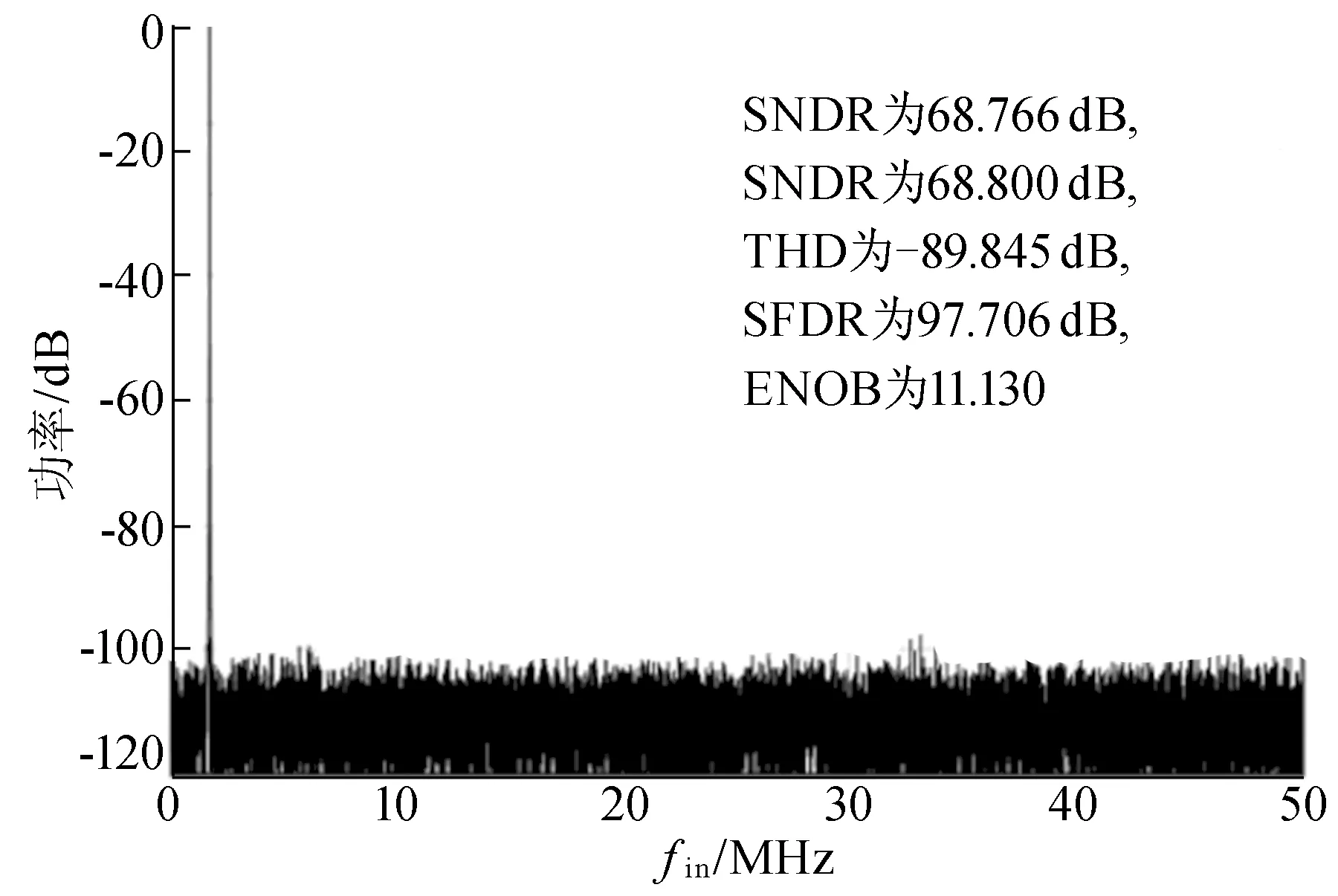
图10 低频时的频谱图

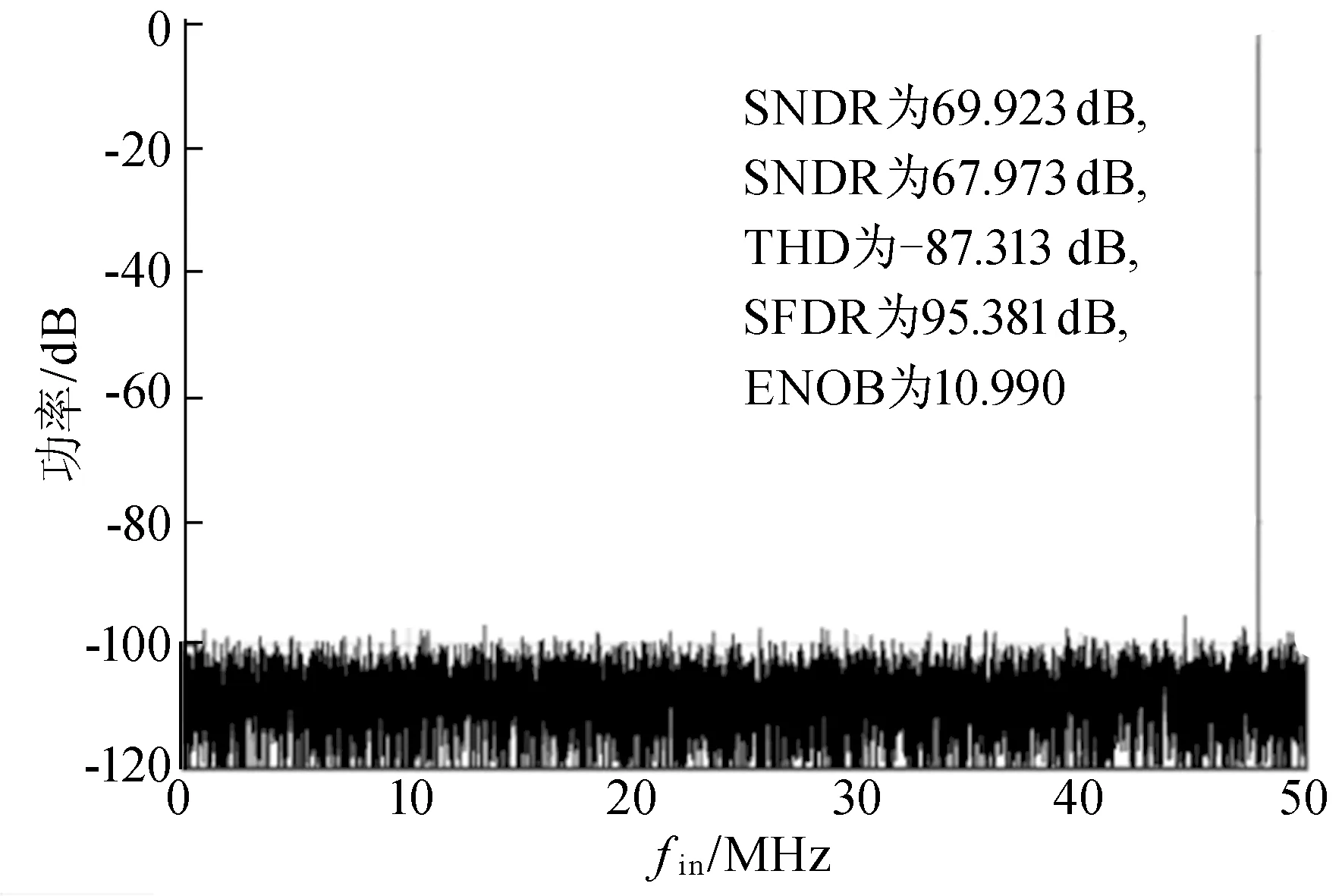
图11 接近Nyquist高频时的频谱图

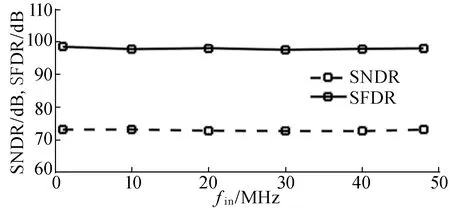
图12 不同输入频率下的SFDR、SNDR变化曲线

本文设计与文献[2,4]设计的ADC性能对比见表1所列。

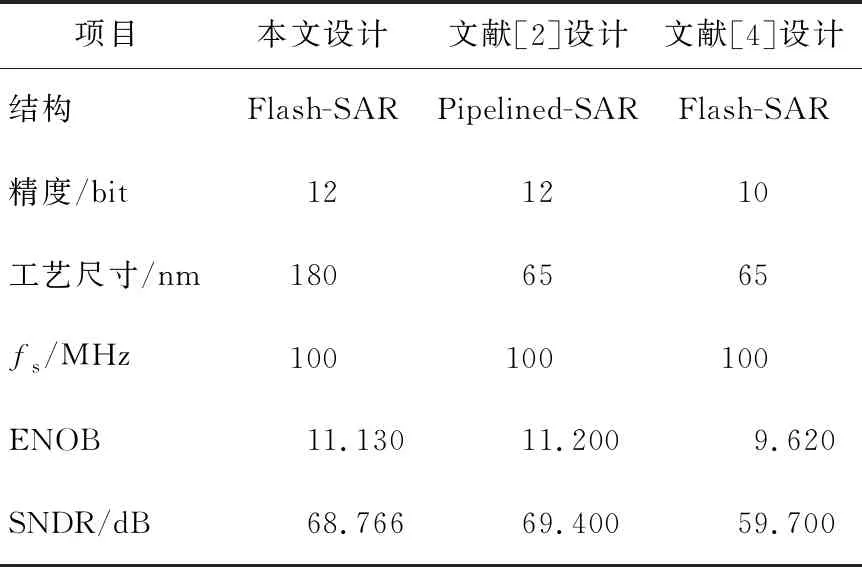
表1 ADC的性能对比

由表1可知,虽然文献[2,4]设计的ADC具有工艺方面的优势,但本文采用SAR ADC带冗余位校准算法后,所设计的混合型ADC的动态性能得到有效提升。

6 结 论

本文在 SMIC 0.18 μm CMOS 工艺下,设计了一款12 bit 100 MS/s Flash-SAR混合型模数转换器,提出了一种SAR ADC 带冗余位数字校准算法,从理论上分析了该校准算法的合理性与有效性,最后的仿真结果也证实了该校准算法的可行性。