下肢康复机器人足底力分布测量装置的研究

黄长建, 赵鹏鹏, 王 勇

(合肥工业大学 机械工程学院,安徽 合肥 230009)

随着老龄化的加剧,脑卒中、颅脑损伤等疾病造成的功能障碍越来越多[1-4],下肢功能障碍对患者生活质量的影响也越来越大。下肢康复训练作为机器人技术与康复医学结合的产物，具有比传统人工医疗师辅助训练更省力、更便捷等优点[5-7]。足底力分布反映了人足部结构以及全身的生物力学功能,是重要的生物力学信息,可用于评定内外翻、足底痛等,对下肢疾病的诊断、康复评定有重要的研究意义。目前,足底力主要的测量装置基本属于独立测评,很少将足底力测量与下肢康复机器人联合使用。足底压力测量主要使用装置包括测力鞋垫、测力板、测力台[8-9]。测力鞋垫是通过在鞋垫底部布置多个传感元件来测量力的分布,但存在传感元件易损坏以及价格昂贵等缺点;测力板和测力台是通过布置力传感器来测量力的分布,但这是一种外在的检测方法,不能实时地监控人的康复情况。

本文设计了可测量足底力分布情况的测量装置,提出了一种通过弹性梁应变来测量足部压力分布情况的测量方法,并且利用有限元仿真来验证该方法的准确性。装置与下肢康复器结合使用,能测量足底力的分布,精度高、使用寿命长,并且能实时监控人的康复情况。

1 足底压力检测装置

足底压力检测装置与下肢康复器联合使用,用装置代替下肢康复器的脚踏板,测量人在使用康复器时的足底力分布,实时地反映人的康复情况。

1.1 检测原理

参考文献[10],足底力分布可以划分为第一跖骨头、第二跖骨头、第三到第五跖骨头、第一趾骨头、第三到第五趾骨头以及足跟等部位。

考虑到实际人体足部趾骨部位在底板外侧,结合压力主要分布区域的情况,选取4个主要测量点,它们分布在第一跖骨头、第二跖骨头、第三到第五跖骨头区域、足跟区域,且这4个区域已经能满足对内外翻等疾病的诊断。其中,第一跖骨头距足跟末端的距离≈足长×72%;第五跖骨头距足跟末端的距离≈足长×64%;足跟距足跟末端的距离≈足长×13%[11];第一跖骨头距脚最左侧距离≈足宽×17%;第二跖骨头距脚最左侧距离≈足宽×52%;第五跖骨头距脚最左侧距离≈足宽×91%;足跟距脚最左侧距离≈足宽×68%。经过查找和对比国家标准中各种型号鞋码所代表的脚宽与脚长以及多个人的足底力分布情况,可以得到4个受力区域的距离关系,进而确定4个测量点的对应位置,如图1所示,不同鞋码对应的距离数据见表1所列。

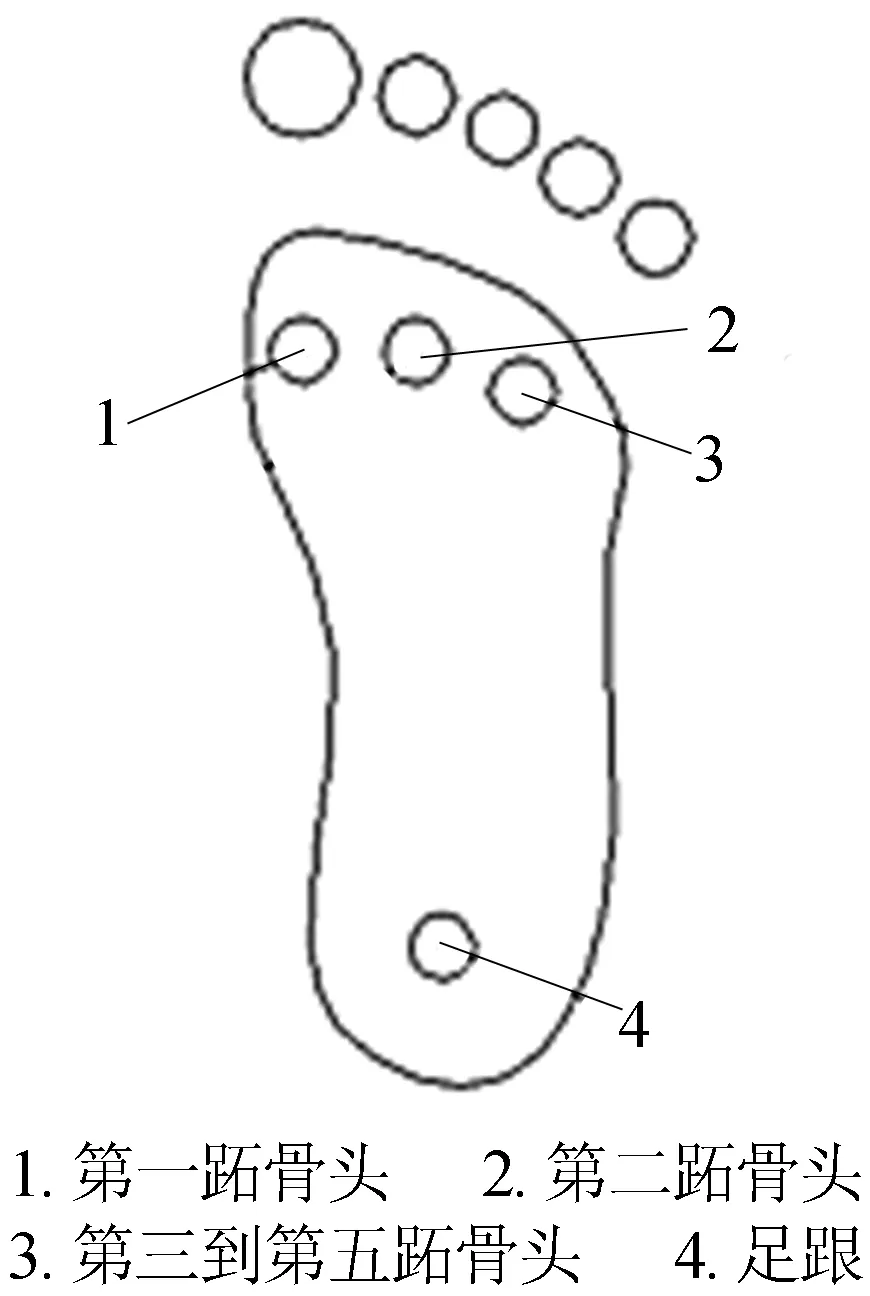
图1 4个测量点的分布位置

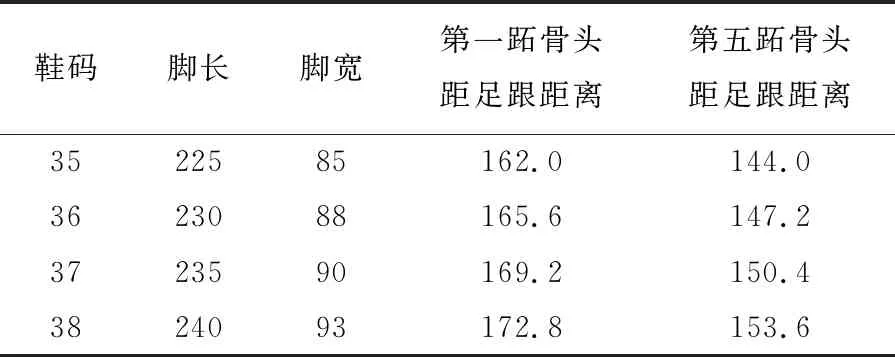
表1 不同鞋码对应的距离mm

下面用38码脚的尺寸进行阐述,确定好在底板上对应的每个相应测量点的位置,以F1、F2、F3、F4代表垂直加载在底板上的力。在各测量点上分别施加力,力的大小均为25、50、100 N,获得对应弹性梁1、梁2、梁3、梁5上的应变,分别为ε1、ε2、ε3、ε4。

加载力在测量点1，获得各施加力与弹性梁输出应变的关系,如图2所示，同理可得弹性梁输出应变与不同测量点的施加力都成正比关系。由悬臂梁应变公式可知应变与力成正比,图2证明了有限元仿真结果真实准确。

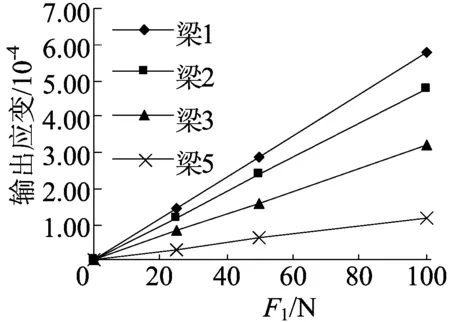
图2 F1对各梁应变的影响

患者在使用下肢康复机器人进行康复训练时,其足部踩在底板上,随底板在电机的转动下运动,然后通过传感器采集相关数据，进而分析运动过程中4个测量点垂直于脚踏方向的力的情况,即可知足底压力分布[12-13]。

1.2 建立装置模型

通过将人足底主要受力区域进行划分,足底装置模型成功建立，足底模型组成部分主要包括弹性梁、底板和支撑。

考虑到各跖骨位置比较接近，不适合在脚底布置多个横梁。为满足测量要求,装置采用悬臂梁。悬臂梁加工简单、重量轻,且能满足测量要求。

为了确定各梁的具体位置,依次对各测量点单独施加100 N的力,得到底板及底板边界的应变情况。通过路径绘制边界的应变图,便于确定最大应变位置，即梁的位置。对测量点1加载力时的应变云图和边界如图3所示。对各测量点加载力时的应变曲线如图4所示。图3中,路径为A到B即1到2；图4中，横轴表示底板边界各点距左侧顶点A的路径距离,纵轴表示路径输出的等效应变的大小。

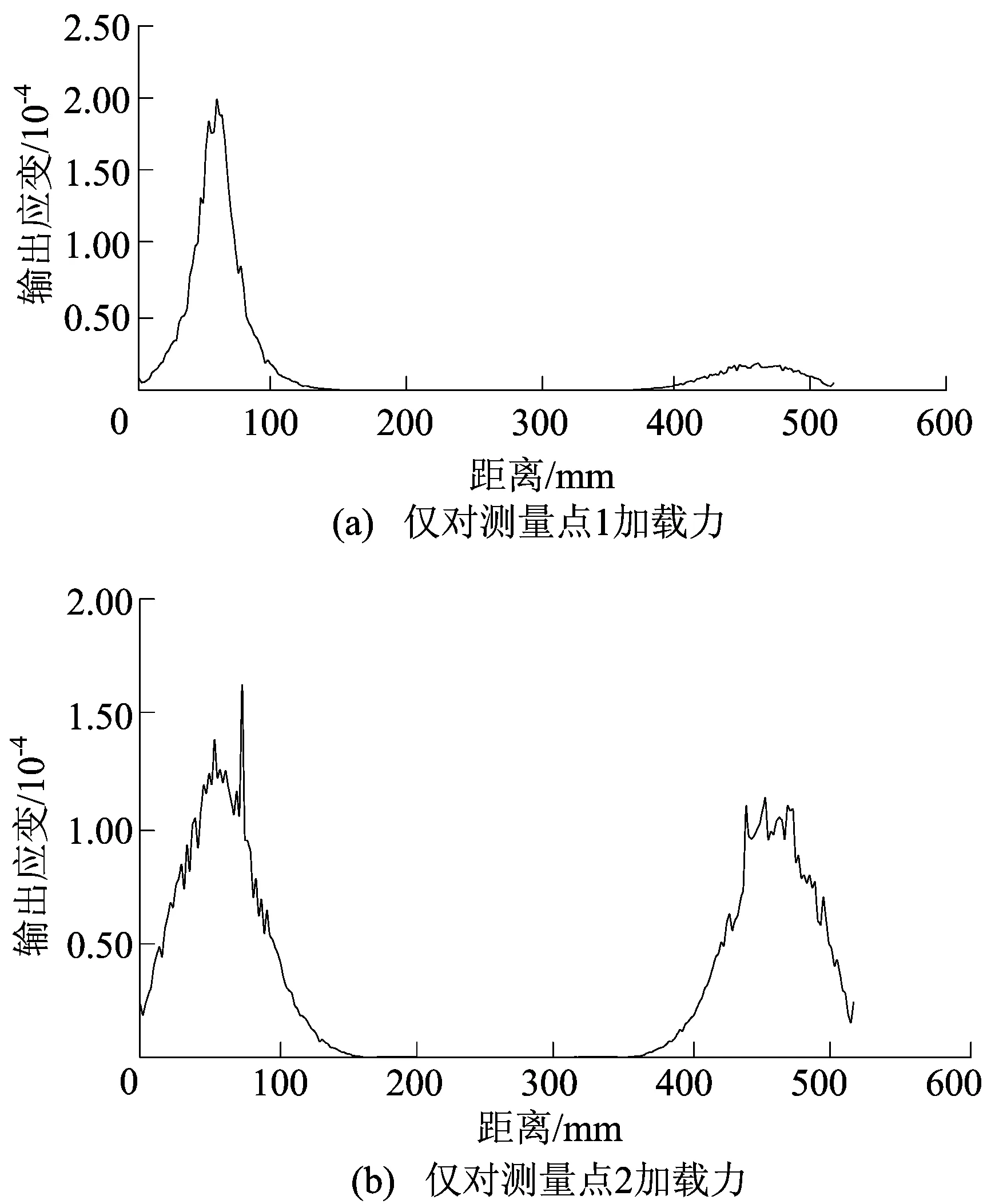
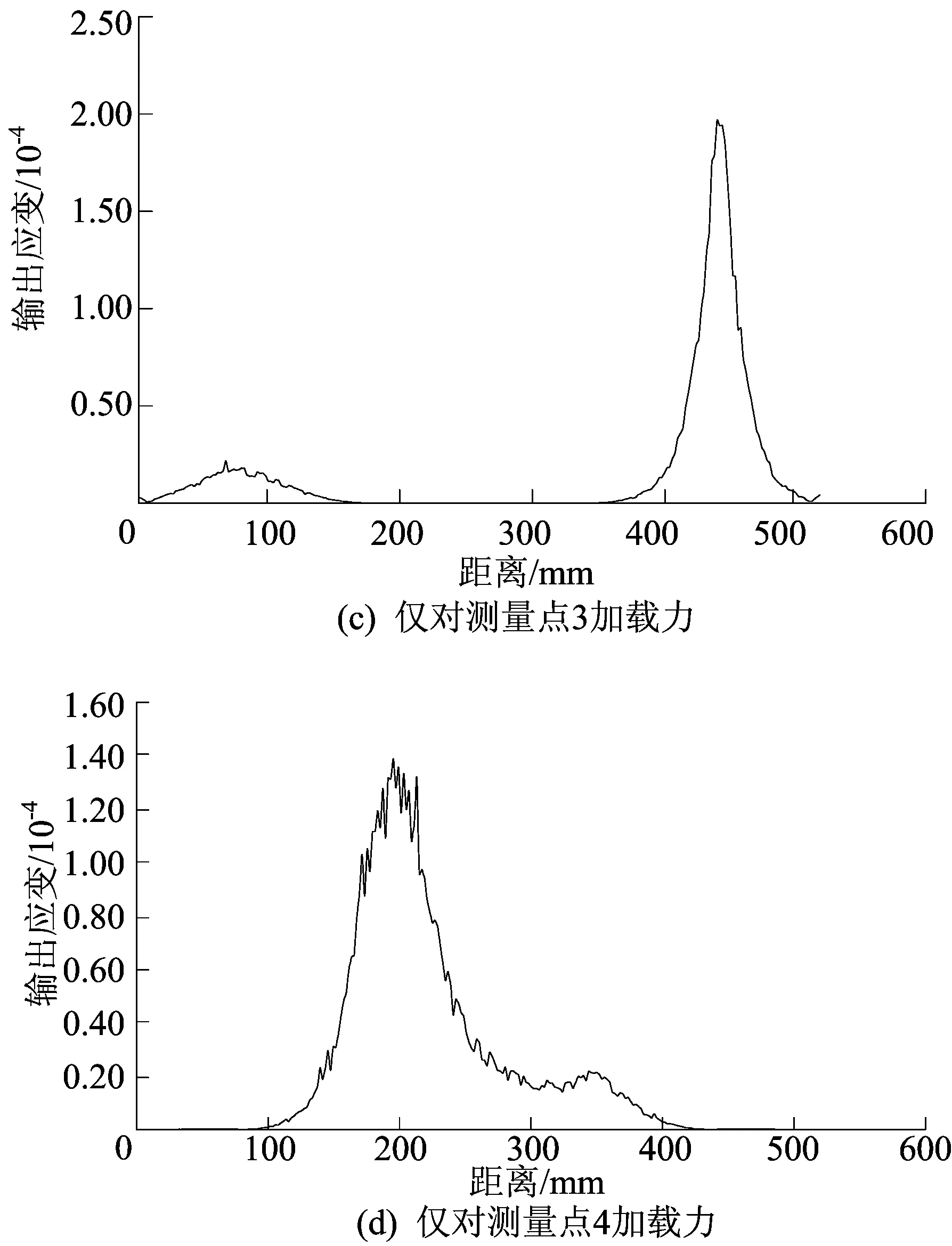
图4 对各测量点加载力时的应变曲线

由图4可以看出在每个测量点加载力时边界的应变变化趋势,为使应变能更好地反映加载力的情况,初步把各梁设置在应变最大处,再对梁的位置进行优化。

本文取38码的尺寸为例进行分析,结合实际情况找到并确定底板上的4个主要测量点的对应位置,并初步设置梁的分布位置。

具体设置的测量点与梁的对应情况为：测量点1由弹性梁1反映；测量点2由弹性梁2反映；测量点3由弹性梁5反映；足跟测量点由弹性梁3和弹性梁4反映,也就是在测量点4的两侧分布对应梁。

对装置模型进行有限元仿真分析使用的材料属性为铝合金LY12,其密度ρ=2.78 g/cm3,屈服强度σs=325 MPa,弹性模量E=71 GPa。

为使加载力能够被各个梁结构精确地测量,对梁结构即长、宽、高进行优化。在底板上对各测量点加载力,经过有限元仿真分析,根据实际情况且以应变尽量大为原则,得到弹性梁的尺寸大小和底板厚度。取梁1、梁2、梁3、梁5尺寸为长9 mm、宽8 mm、高2.8 mm,梁4尺寸为长9 mm、宽5 mm、高2.8 mm。

通过理论分析和机构优化最终确定弹性梁的分布位置及尺寸大小,确定优化后的数学模型,结果如图5所示。

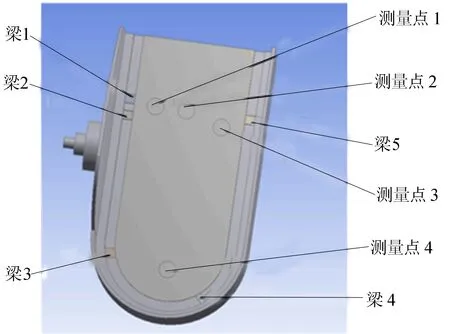
图5 改进后的脚踏模型

1.3 仿真分析

分别施加100 N的力在底板4个测量点上,对底板模型进行仿真分析，得到的应力分布云图如图6所示。

图6 对测量点1加载力的应力分布云图

从图6可以看出,施加力到测量点1时,模型的应力主要分布在弹性梁1、梁2、梁5上;同理可得,施加力到测量点2时,应力主要分布在弹性梁1、梁2、梁3、梁5上;施加力到测量点3时,应力主要分布在弹性梁1、梁2、梁3、梁5上;施加力到测量点4时,应力主要分布在弹性梁1、梁2、梁3、梁4上,与前面几个测量点加载力相比,梁1、梁2上分布的应力较小。由上述分析可知,足前掌的3个测量点的力对梁1、梁2、梁5影响较大,对梁3、梁4影响较大的是足跟作用力。由仿真分析可知,对每个测量点加载力时,应变都集中在各个梁上,证明了装置设计的有效性。

2 足底压力检测方法

2.1 数学模型

根据梁应变与测量点加载力的线性关系构建数学模型C4×4F4×1=ε4×1,ε为输出应变矩阵，F为加载力矩阵，C为常数矩阵,即

(1)

通过施加大量不同大小的力于各测量点,获得对应弹性梁输出的应变,再由(1)式获得各系数。为使常数矩阵更好,采用正交试验对各梁位置进行优化。

由于在矩阵的求解中系数矩阵的条件数对求解影响很大(条件数越小，求解越准确；条件数过大,矩阵就变成病态矩阵),以梁初始位置为起点,规定向底板前端为正,向底板后端为负,变动幅度为梁1与梁2间距的1/2,取每个因素的水平数为3。试验指标为矩阵的条件数cond(C,2)。正交试验水平见表2所列。

表2是一个4因素3水平的试验,选用L9(34)型正交表,正交试验结果见表3所列。

表2 正交试验水平 mm

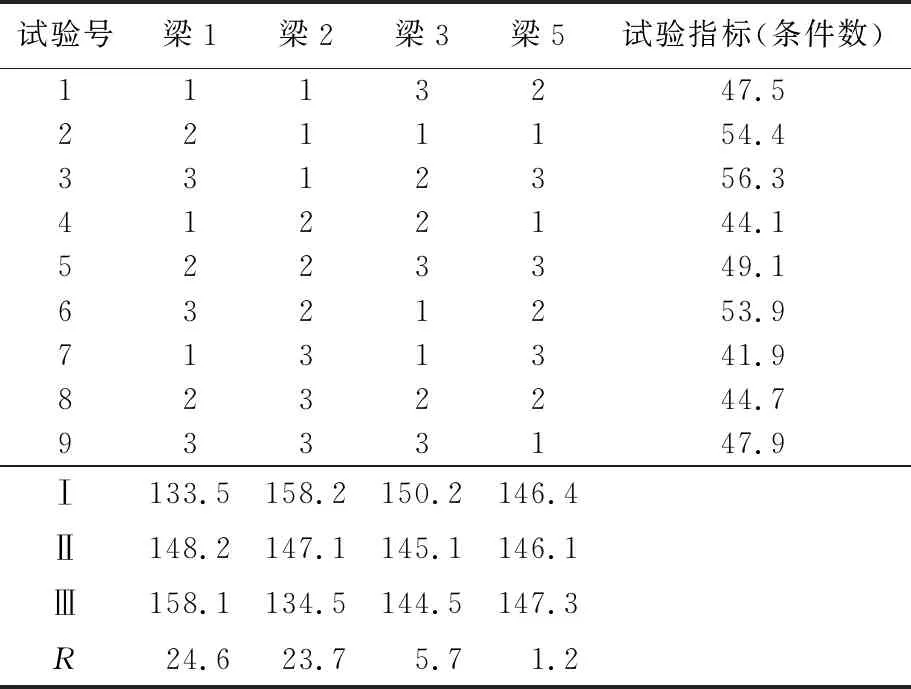
表3 正交试验结果

从表3可以看出,梁1和梁2对试验指标影响较大；而在7号试验各梁的组合水平时，试验指标即条件数最小,此时为最优解,各梁的优化位置确定。

以矩阵的条件数cond(C,2)为试验指标，计算得到梁的最优位置,通过矩阵求解得到最优矩阵,矩阵C4×4结果为:

实际对足底压力测量时,在图3中弹性梁1、梁2、梁3、梁5的上、下两面对称粘贴应变片。由于试验过程中存在非线性误差,为消除该误差,构建惠斯通半桥电路。通过采集系统得到输出信号并经过相应处理获得对应弹性梁上的输出应变ε,根据(1)式计算获得各测量点的受力大小。为了方便分析评价,保留经过相应处理得到的足底压力分布信息,以便反映相关的生物信息。对于不同的脚码,区域位置和常数矩阵有相应的变化,设计采用一个脚码对应一个装置的原则。

2.2 仿真验证

施加5组不同大小的力在各测量点上,经过仿真分析可以获得各个弹性梁上输出应变ε的情况,结合(1)式和常数矩阵C4×4计算得到应变ε′,并将仿真值ε与计算值ε′进行比较,对比结果见表4所列。其中力的单位为N,下文同。

从建立的数学模型可以获得在使用装置时足底各受力点的受力情况F′,将有限元仿真分析得到的仿真值F与计算得到的计算值F′进行比较,结果见表5所列。

表4 应变的仿真值和计算值

表5 加载力的仿真值和计算值

从表4、表5可以看出,经计算得到的应变与仿真得到的应变误差小于0.1%;经计算得到的力与仿真得到的力的误差为0.074%～2.5%。

3 试 验

在各梁上对应贴好应变片后,选择恰当的电阻,根据惠斯通半桥电路的连接方法,合理连接4个惠斯通半桥回路,结果如图7所示。

图7 应变片粘贴与桥路搭建后的装置

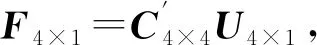
(2)

为提高数学模型的计算精度,对其进行优化,使加载力与通过计算的加载力误差最小,建立目标函数。Fi=ai1U1+bi2U2+ci3U3+di4U4,其中i=1,2,3,4，目标函数如下所示:

(3)

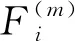
(4)

在各测量点上施加15组不同的力,记录各组力的大小,将其作为理论加载力F理论=[F1F2F3F4]T。把每组对应的4个桥路的输出电压代入数学模型F4×1=C4×4U4×1中计算力的大小,得到试验值F试验=[F1F2F3F4]T。将F理论与F试验进行比较,结果见表6所列。

由表6可知,利用优化后的数学模型和试验测得的输出电压求解获得的力与实际过程中加载力的大小存在误差,误差范围为±0.1%～±7.30%。分析误差存在的原因有梁上应变片粘贴的质量、结构加工的精度、砝码的精度以及半桥桥路本身就有一些温漂环境干扰等。

在误差可以接受的情况下,数学模型基本能够得到足底力大小的分布情况,同时也证明了本文测量装置和方法的可靠性和准确性。

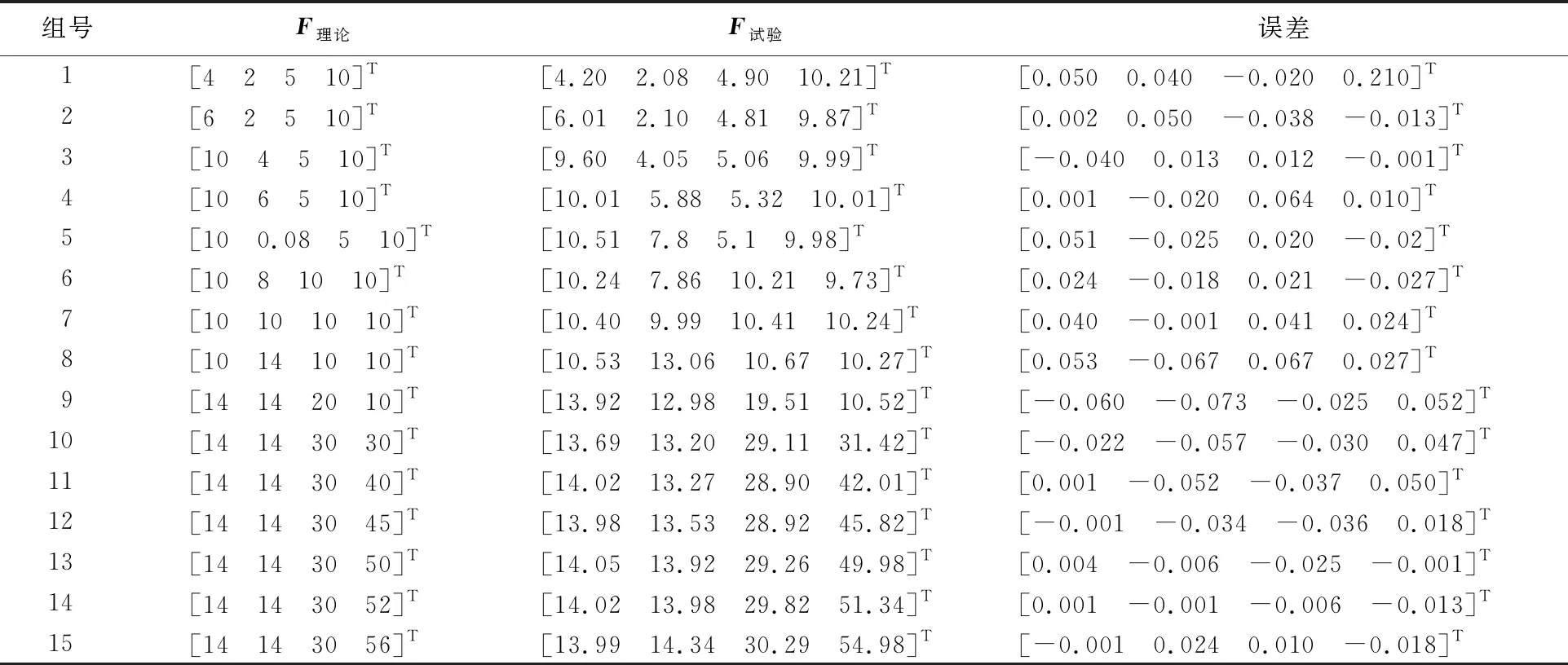
表6 计算所得力与试验加载力及其误差

5 结 论

本文分析了足底力分布情况,设计了测量足底压力的装置；经过理论分析得到并验证了各弹性梁上应变与力的关系,建立了数学模型C4×4F4×1=ε4×1；对检测装置输出的信号进行了相关采集与处理。试验结果精度较高,证明了本文方法和装置的可靠性与准确性。该装置与下肢康复机器人结合使用,可以实时得到训练过程中足底力的分布情况,具有一定的实用价值和研究意义。