基于广义Bézier方法的车灯轮廓设计

刘 植, 王楚涵, 陈晓彦, 邢 燕

(合肥工业大学 数学学院,安徽 合肥 230601)

0 引 言

汽车的车灯设计直接决定了汽车的整体“气质”,圆形的车灯显“呆萌”,柳叶形和三角形的车灯显“狂野”。20世纪30年代,汽车车灯形状主流为圆形,20世纪80年代起,汽车车灯形状开始与整个车身的造型相协调,出现了矩形、椭圆、菱形等各种风格。汽车车灯形状的多样化,使车灯从一辆汽车的基本配置,变成了一个更加能够体现个性化的因素。因此,汽车车灯形状的设计会直接影响汽车的销售及品牌效应,个性化的需求需要产生足够多的设计样本以供设计师参考。

20世纪60年代后期,法国雷诺(Renault)汽车公司的工程师皮埃尔·贝塞尔(Pierre Bézier)结合数学方法描绘出了Bézier曲线。该方法首先建立曲线的特征多边形,通过修改控制顶点的位置改变曲线的收敛方向,可以达到快速获得多种设计形状的目的,具有极强的直观性和便利性。与传统手绘方法相比,虽然Bézier方法已经极大提高了设计师的工作效率,但在光滑连接问题和细节调整方面仍有不足。为了改善此问题,众多研究者利用Bézier曲线的几何不变性提出一系列基于带参数多项式的曲线优化设计方法。

文献[1]用三次Q-Bézier曲线描述了汽车车灯造型轮廓;文献[2]用四次带参Bézier曲线统一描述了汽车前脸各造型设计元素轮廓;文献[3]讨论了一类双参数三次Bézier曲线的形状;文献[4]提出基于四次带参广义Bézier曲面的汽车造型设计方法;文献[5]提出一种加权Lupasq-Bézier曲线,和传统方法相比,在相同控制点下的逼近性有一定程度提升;文献[6]提出带有多个形状参数的扩展Bézier类曲面及其连续性条件;文献[7]提出带2个形状参数的同次Bézier曲线;文献[8]研究了一类基于三次拟Bézier方法的汽车车灯轮廓设计,该方法描述形状的调配函数是4个线性无关的三次多项式函数,对图形的张力表示和流畅性均有所加强,其不足之处在于,G2连续时和已有方法存在同样的弊端——确定控制顶点时需要求解大型方程组,计算量大,不利于设计后期细节的调整,且难以满足整体C2连续性要求。

本文在已有设计方法基础上,提出了汽车车灯形状设计的一种新算法。首先,结合四次广义Bézier曲线定义及性质,研究分析了曲线的参数连续条件;然后,讨论了控制点以及参数的改变对车灯形状的影响;最后给出几种设计实例。本文算法通过调整控制顶点的位置和修改形状参数的取值来获得车灯形状设计的多种方案,该算法可以应用于汽车造型设计中的其他造型元素,拓展性较强。

1 四次广义Bézier曲线

定义1[9]给定1组控制顶点{D0,D1,…,D4},记

r(t)=r(t;λ,μ)=

则称r(t)为带形状参数λ、μ(λ,μ∈(-3,1])的四次广义Bézier曲线,简称四次广义Bézier曲线,其中调配函数为:

特别地,当形状参数λ、μ均取1时,四次广义Bézier曲线即是四次Bézier曲线。可以验证上述调配函数具备线性无关性,且等价于四次Bernstein基函数,因此四次广义Bézier曲线是建立在四次Bézier曲线基础上的推广。对于给定的控制顶点,要得到不同形状的曲线只需要相应调节控制参数的值。

由调配函数的形式可以看出:

(1) 参数λ的值仅与b0,4(t;λ,μ)、b1,4(t;λ,μ)有关。λ越大,b0,4(t;λ,μ)越小,而b1,4(t;λ,μ)越大,此时生成的曲线更加靠近控制点D1。

(2) 参数μ的值仅与b3,4(t;λ,μ)、b4,4(t;λ,μ)有关。μ越大,b3,4(t;λ,μ)越大,而b4,4(t;λ,μ)越小,此时生成的曲线更加靠近控制点D3。

形状参数不同取值对四次广义Bézier曲线形状的实际影响如图1所示。

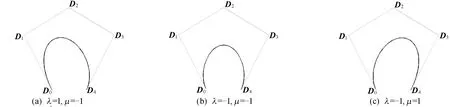
图1 λ、μ取不同值时图形不同偏向情形

定理1记di=Di-Di-1,则四次广义Bézier曲线在端点处满足:

(1)r(0)=D0,r(1)=D4。

(2)r′(0)=(λ+3)d1,r′(1)=(μ+3)d4,即四次广义Bézier曲线插值首、末端点,且与首、末控制边相切。

(3)r″(0)=6[2d2-(λ+1)d1],

r″(1)=6[(μ+1)d4-2d3]。

2 汽车车灯形状曲线的设计

车灯轮廓曲线可看作在一定光滑性条件下的封闭曲线,因此可以把汽车车灯形状设计问题归类为在一定连续条件下四次广义Bézier闭样条曲线的构造问题。具体步骤如下:① 根据车灯形状设计的要求描绘车灯形状草图,也就是依次连接控制顶点获得控制多边形;② 根据算法选取每段曲线的控制顶点和形状参数,以便在控制多边形凸包内得到满足一定光滑性要求的闭样条曲线;③ 车灯设计要体现强烈的个性特点,并且要和整部车的风格相符合,从而表现出汽车潜在的品牌效应。通过以上设计步骤,绘制的车灯形状线条往往比较粗糙,需要进一步调整形状参数数值或控制顶点坐标,以达到车灯形状曲线的整体或者局部修正。这样多次调整和修改后,得到的满足设计初衷和需求的四次广义Bézier闭样条曲线即车灯形状曲线。

在实际设计中,要保证插值样条曲线间的光滑过渡,就需要考虑曲线光滑过渡的连续性。采用已有各种设计方法在绘制C1连续的轮廓曲线时快捷灵活,但对C2连续的情形,已有方法涉及得相对较少。为了说明本文方法的可行性,以下主要讨论C2连续的车灯形状曲线交互设计。

基于四次广义Bézier方法的形状可调C2连续汽车车灯轮廓设计步骤如下:

(1) 根据设计需求,选取车灯轮廓控制顶点Dj(j=0,1,…,n),其中Dn=D0,Dn+1=D1,绘制车灯轮廓闭多边形{D0,D1,…,Dn}。

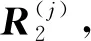
(3) 取形状参数λj、μj,需满足-1≤λj≤1和-1≤μj≤1。

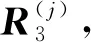
其中,λn+1=λ1。

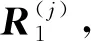
其中,μ0=μn。

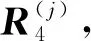
国内生产总值从0.37万亿元增长到82.7万亿元，国家财政收入从0.11万亿元增长到17万亿元，城镇化率从17.92%增长到58.52%……

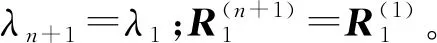
(8) 生成C2连续四次广义Bézier闭样条车灯轮廓曲线,即

为了生成车灯轮廓闭多边形{D0,D1，…,Dn}保形的闭样条曲线,同时为了简化设计过程,上述步骤将形状参数λj、μj限制在闭区间[-1,1]上。上述方法设计的车灯轮廓曲线的形状调控简单易行,对于给定的初始车灯轮廓闭多边形{D0,D1,…,Dn},生成的车灯轮廓曲线形状交互控制方法如下:

(1) 通过改变形状参数的取值调整曲线的形状。形状参数的取值决定了其生成曲线的局部形状特征,如前所述,形状参数λj、μj(j=0,1,…,n)在定义范围内取值越大,生成曲线越靠近相应控制顶点。

调整控制顶点与调整形状参数相结合,相辅相成可以绘制出形状更加丰富的车灯形状曲线。每段曲线的控制点由初始轮廓控制点直接计算生成,计算方便简洁。

3 造型设计实例

为了适应现代汽车造型设计的丰富多样和满足人们不一而足的审美需求,设计师们需要一种便于操作、快速有效的程序化设计方法,并且要满足后期修改有充分的自由度。本文方法可以生成满足一定光滑性要求的车灯轮廓曲线,且容易实现轮廓曲线的整体与局部形状修改。

为实现闭样条曲线修改的目的,本文主要强调改变每段四次广义Bézier曲线首、末控制顶点或切点的位置,也就是修改切点位置参数ωj的取值以及形状参数λj、μj(j=0,1,…,n)的取值来实现形状控制。

四次广义Bézier样条轮廓曲线及其不同调整方式的效果如图2所示。图2a所示为车灯形状设计的第1次草图,对应参数ωj=0.15,λj=μj=0(j=0,1,…,n);图2b～图2e所示为调整λ、μ值后得到的效果图。

比较图2a和图2b可知,相同条件下,λ增大,曲线更接近P点、Q点,远离S点,下凹明显。

比较图2b和图2c可知,相同条件下,μ减小,曲线更接近S点,远离P点、Q点,较平滑。

比较图2a和图2d可知,相同条件下,μ增大,曲线更接近Q点、S点,远离P点,棱角明显。

比较图2d和图2e可知,相同条件下,λ减小,曲线远离P点、Q点,更接近S点,线条较直。

比较图2c和图2d可知,相同条件下,λ减小,曲线远离P点、S点,更接近Q点,棱角明显。

对相同控制点,固定λj=μj=0取值,调整ωj取值为0.35、0.50、0.65后的曲线如图3所示。

比较图2a和图3可知,相同条件下,ω增大,曲线越来越接近Q点,线条也趋近平滑饱满。图3c的曲线更加饱满,图2a的曲线更具有流线型特点,可分别适用于不同的车型。

综上所述,若要极大提高弧度感 ——“饱满”的车灯形状,则可通过增大ω值实现;若只是让车灯线条稍微圆润一些,则可通过增大λ或者减小μ,实现局部微调而不影响车灯整体风格。由于消费者审美具有多样性,本文算法能实现通过修改1个参数值迅速获得多种风格设计图,相比于传统通过修改控制节点坐标的方法,不仅极大地节省了人力,还能提供更多的设计灵感。

将生成的样条曲线投影到汽车表面上,最后通过对引擎盖板、前裙板、前翼子板这3块曲面进行修剪可以获得车灯的轮廓造型。对于设计师而言,由于只需要在一个二维平面上对轮廓曲线进行编辑和修改,以满足不同的产品需求,比在三维空间中调节曲线曲面要方便很多。

采用本文算法对汽车车窗、车前盖进行设计,同样可以通过调整参数取值和控制顶点改变设计形状。对相同的控制点,相同的参数λj=μj=0,车窗设计如图4所示,车前盖设计如图5所示。

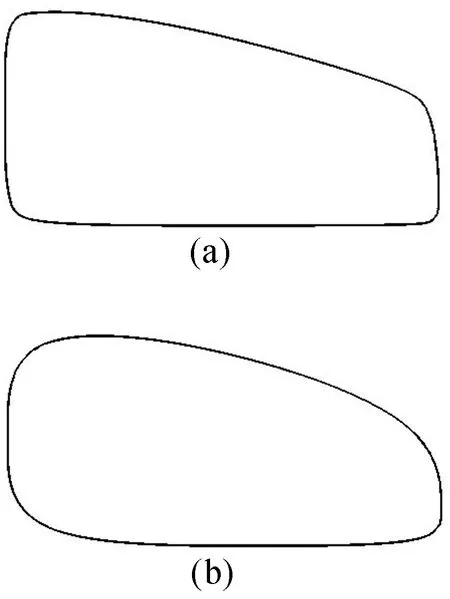
图4 车窗设计效果

图4a、图5a中ωj取值为0.1、0.5、0.1、0.5、0.1、0.5、0.1、0.5,图4b、图5b中ωj取值均为0.5。

图5 车前盖设计效果

4 结 论

与传统的绘制与调整方法相比,本文通过调整四次广义带参Bézier曲线中控制顶点的位置和形状参数,可以迅速获得不同的线条形状,从而得到大量不同风格的汽车车灯造型。该方法同样适用于汽车车身其余部分的绘制,如车窗、前盖的设计等,具有较强的扩展性;与已有同类方法相比,车灯曲线每个点依赖于初始控制点,逼近性效果更理想,在此基础上,可以实现更好的细节修改,从而尽量减少对其余已完成形状设计的影响。