基于行驶特征预测的HEV在线控制策略研究

张冰战, 蒋 通, 李开放

(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)

混合动力汽车(hybrid electric vehicle，HEV)由于其节能、低排放等优点引起了汽车产业的极大关注,已成为目前新能源汽车研发领域的热点之一[1]。

为了能够充分发挥混合动力汽车的节油潜力、协调动力源间的动力分配,高效合理的控制策略成为了目前国内外混合动力汽车研究的核心之一[2]。为此,相关学者进行了大量研究。文献[3]采用学习向量量化(learning vector quantization,LVQ)神经网络识别工况,结合动态规划(dynamic programming,DP)的结果,提取不同工况下的功率均衡控制规则对整车进行控制;文献[4]应用遗传算法优化后的K均值聚类分析对行驶工况进行识别,结合等效燃油最小能量管理策略(equivalent consumption minimization strategies,ECMS)实现各个工况下的发动机和电机功率的实时优化分配;文献[5]采用模糊识别算法进行行驶工况的在线识别,并根据最小等效油耗控制算法和电池电量平衡控制方法调用相应的最优控制参数,实现了发动机和电池功率的实时优化计算。从以上研究可以看出,研究人员在开发控制策略时均希望通过考虑行驶工况来改善车辆的燃油经济性。因此如何有效识别车辆的行驶工况成为制定合理混合动力汽车控制策略的关键。

本文在已有研究的基础上,综合考虑行驶工况和行驶模式2类行驶特征对车辆燃油经济性的影响,构建了行驶特征的预测模型。以某HEV为研究对象,研究了DP算法下的全局最优控制策略,在此基础上结合车辆行驶特征的预测,解决了全局最优控制策略的在线应用问题。

1 标准行驶工况的选取

在HEV方面,国际上研究人员通常借鉴美国环保局提供的11种典型(faclity specific,FS)行驶工况[6],分别为高速(Freeway)6种、高速匝道(Freeway-Ramp)、本地(Local)、主干道(Arterial)3种。根据便利性(facility)和服务性(level of service)将Freeway工况分为6种子工况,分别为A、B、C、D、E、F,其中A代表最好的驾驶环境,F代表最差的驾驶环境;类似地,Arterial工况被分为3种子工况,分别为AB、CD、EF。本文同样以此11种工况作为标准,且为方便描述,将它们依次记作A、B、C、D、E、F、Ramp、Local、AB、CD、EF工况。

2 基于DP算法的最优控制策略

2.1 DP算法模型

HEV的控制本质上是一个在一定约束条件下油耗与排放的最优控制问题[7]。在行驶工况已知的前提下,车轮需求转矩和传动系统需求转速是确定的，因此选取系统状态变量和控制变量为:

x(k)=SOC(k)

(1)

u(k)=(Tm(k),R(k))

(2)

其中,x(k)为系统k阶段状态变量;u(k)为系统k阶段控制变量;SOC(k)为系统k阶段电池SOC;Tm(k)为k阶段的电机转矩;R(k)为系统k阶段的传动比。状态变量传递函数为:

(3)

其中,I(k+1)为系统k+1阶段的电流;C为电池的容量。本文所研究的全局最优控制策略以燃油消耗最小为目的,不考虑其排放。因此定义阶段代价函数如下:

L(x(k),u(k))=Qfuel(k)

(4)

其中,Qfuel(k)为系统k阶段的油耗。

为保证良好的驾驶性能,在代价函数中加入了换挡约束。附加代价函数Ls(k)为:

Ls(k)=|shift(k)|

(5)

其中,shift(k)可取1、-1、0,分别代表升挡、降挡、保持原挡。k阶段目标函数为:

(6)

其中,λ为正的加权益子,需要经过大量的试验反复调整。最优目标函数和边界约束条件分别为:

fk=min(Jk,N)

(7)

(8)

根据最优目标函数,DP算法在其边界约束条件下进行离线最优轨迹的求解。

2.2 标准工况的离线最优轨迹求解

2.2.1HEV结构及主要参数

本文的研究对象为某单轴并联式HEV,其动力系统结构如图1所示。其中发动机与电机同轴相连,离合器闭合时,发动机与电机转速相同。整车及零部件主要参数见表1所列。

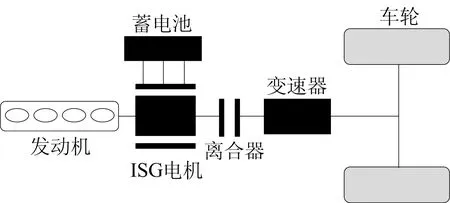
图1 HEV动力系统结构

表1HEV整车及零部件参数

部件参数数值整备质量/kg800迎风面积/m21.9整车风阻系数0.25滚动半径/m0.275传动系统传动比11.106 6,5.617 5,3.231 0,2.760 6,2.270 1 排量/L1.0峰值功率/kW50发动机峰值功率时转速/(r·min-1)5 700峰值转矩/(N·m)89.5峰值转矩时转速/(r·min-1)4 800电机峰值转矩/(N·m)46.5峰值功率/kW49电池容量/(A·h)6.0标称电压/V144

2.2.2 标准工况离线最优轨迹

根据整车及部件参数和DP算法原理,通过Matlab编程实现其离线最优轨迹的求解。在Matlab/Simulink中搭建了全局最优控制器“DP-Strategy”,如图2所示。将此控制器嵌入ADVISOR整车模型中进行联合仿真,为了充分考察HEV的燃油经济性,设定仿真时电池SOC始末值均为0.7。

分别对11种FS标准工况应用DP算法求解离线全局最优控制变量序列,为下文搭建的在线控制策略做准备。标准工况Arterial CD仿真结果及各标准工况的油耗如图3所示。在图3d中,1为基于规则的电机辅助控制策略;2为全局最优控制策略。

图2 DP-Strategy控制器Simulink模型

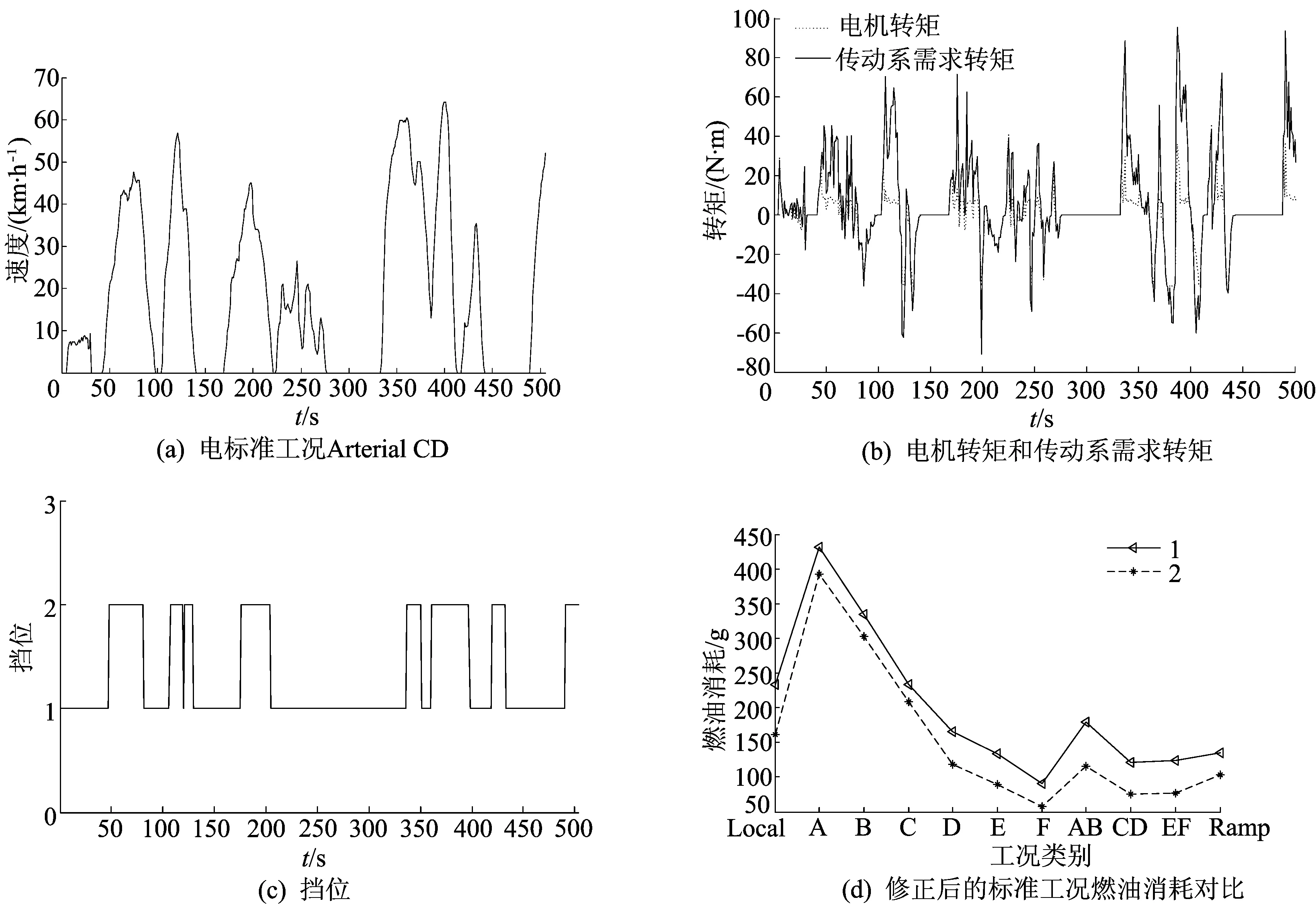
图3 标准工况Arterial CD仿真结果及各标准工况油耗

结合图3a的车速可以看出，图3b、图3c比较符合工况的需求。由图3d可知,相比于基于规则的电机辅助控制策略,应用本文所设计的全局最优控制策略车辆燃油经济性均有不同程度的提高,其中提高幅度最大为38.0%(工况CD),最小为9.0%(工况A)。这说明基于DP算法的全局最优控制策略通用性良好,且在各标准工况下车辆燃油经济性均得到了提高,可以作为在线控制策略研究的基础。

3 行驶特征预测模型

3.1 行驶工况预测模型

3.1.1 行驶工况特征参数的选取

本文假设未来1～2 min内车辆行驶工况不发生变化[8],以上述11种标准行驶工况为标准数据库,为了能对各种工况类别进行准确地预测,经过研究[9-10],本文选取的工况特征参数见表2所列。表2中，速度单位为km/h，加速度单位为m/s2，下文同。

表2 工况特征参数

3.1.2 行驶工况预测模型

文献[8]发现,若选取的工况采样时间太小,则可能无法正确包含循环工况的特征信息;而若选取的采样时间太大,则在实时控制时计算量太大。当特征参数采样时间长度接近或超过3 min时能够较好地反映当前行驶工况[11],因此本文选择ΔT为150 s,并且可以叠加[12],预测时间为1 s。

本文采用运算方便、实用性较强的Euclid贴近度进行行驶工况的预测,将与当前工况最为类似的标准工况作为未来一段时间的行驶工况类别。设Si(i=1,2,…,11)为标准数据库中的样本，M为待识别的样本即车辆实际行驶工况,则Si与M之间的Euclid 贴近度σ(为了消除各特征参数的量纲、数量大小以及变化幅度对贴近度比较的影响,利用min-max标准化函数对原始数据进行标准化)表示为：

(9)

其中,n为循环工况特征参数数量。

根据 Euclid 贴近度公式计算出的Si与M两者之间的贴近度,若存在σ(Si,M)=max{σ(S1,M),σ(S2,M),…,σ(S11,M)},则认为M的工况类别属于标准工况Si。

3.2 行驶模式预测模型

3.2.1 行驶模式分类

行驶模式是驾驶员对短期内道路环境的一种反映,是汽车的一种重要状态。在一个较长的行驶工况中,根据具体的时段、天气等差异,短时间工况内会呈现不同的运动特征。本文将行驶模式定义为5个类型[13],见表3所列。

表3 行驶模式类型

3.2.2 BP神经网络

反向传播(back propagation,BP)神经网络是一种误差逆向传播算法训练的前馈神经网络,具有任意复杂的模式分类和优良的多维函数映射能力,目前被广泛使用。本文采用的3层BP神经网络结构示意图如图4所示。其中,I表示网络的输入层,H表示隐含层,O表示网络的输出层;X为网络的输入,Y为网络的输出。

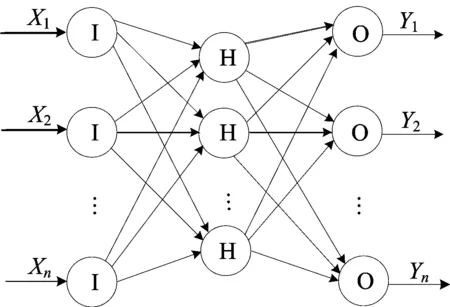
图4 BP神经网络结构

3.2.3 行驶模式预测模型设计

针对11种标准工况,根据文献[14],选取了6个特征参数用来描述[t-ΔTDT,t]内车辆的运动特征,分别为该时间段内的平均车速、最大车速、最小车速、平均加速度、t-ΔTDT时刻的车速及t时刻的车速。将此6个特征参数作为模型的输入,以相应的行驶模式类型作为输出。另外,本文对行驶模式的类型进行二进制编码[15]。

为了确定最佳的ΔTDT值,本文采用试凑法对ΔTDT进行了试验,试验结果如图5所示。其中,网络的测试工况数据有11种:① UDDS;② HWFET;③ US06;④ SC03;⑤ LA92;⑥ IM240⑦ Rep05;⑧ NY City;⑨ HL07;⑩ Unif01;Arb02。

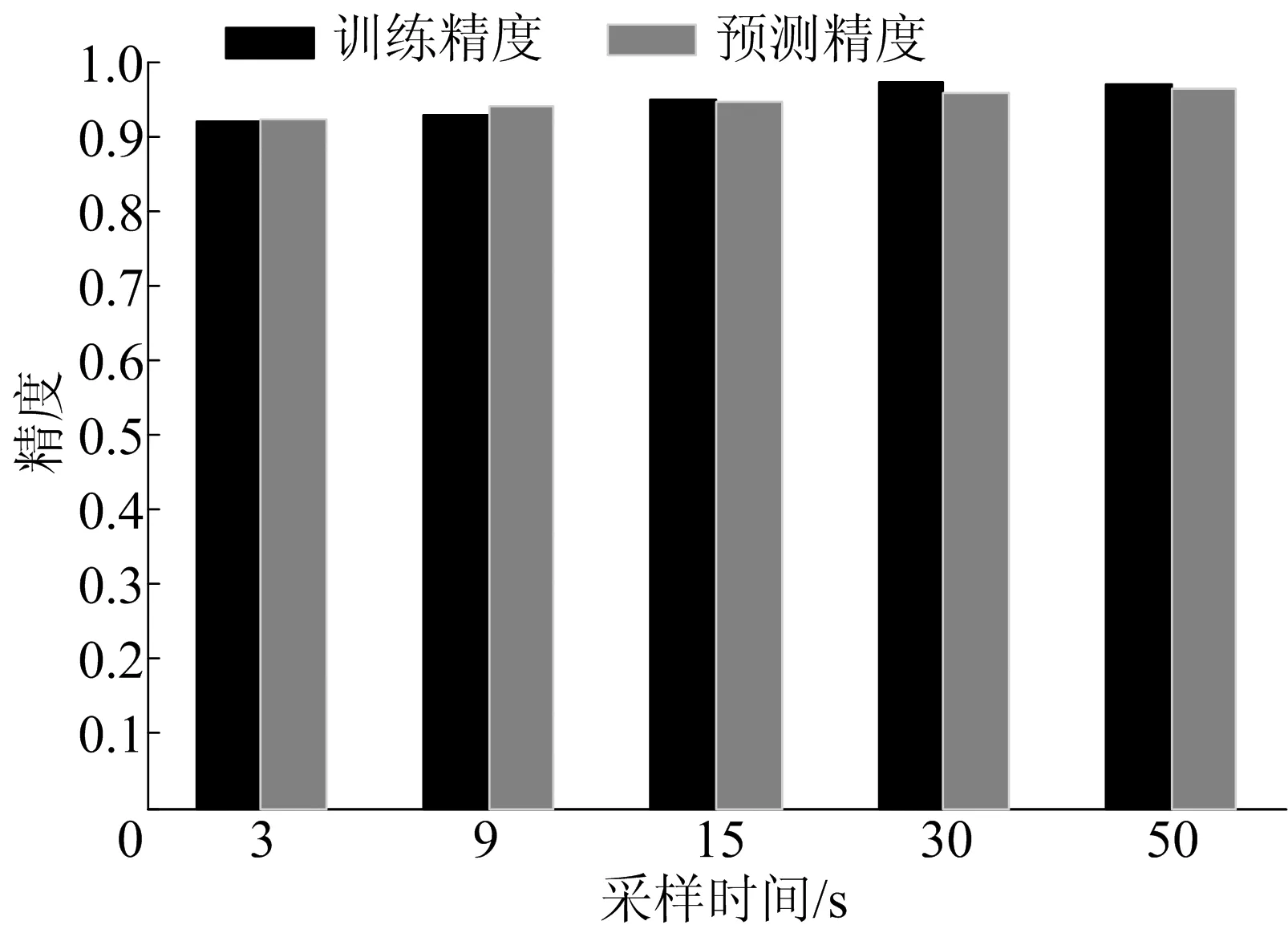
图5 不同采样时间窗口的精度

综合考虑不同时间窗口下训练精度和测试精度结果,最终选取最佳采样时间ΔTDT=9 s。

4 综合在线控制策略

4.1 离线最优轨迹的在线应用控制模型

本文对电机转矩和传动系统传动比进行在线控制模型的设计。采用BP神经网络方法,分别对11种标准工况下离线最优轨迹进行拟合,以期达到离线最优策略的控制效果。本文设计的基于BP神经网络的在线控制模型示意图如图6所示。

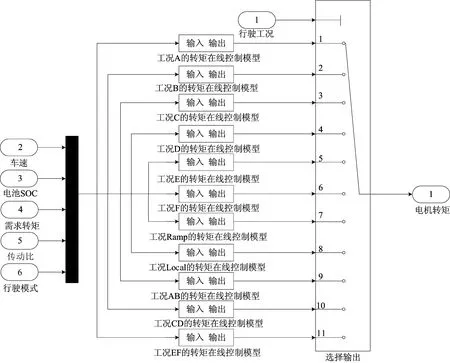
(a) 电机转矩在线控制模型

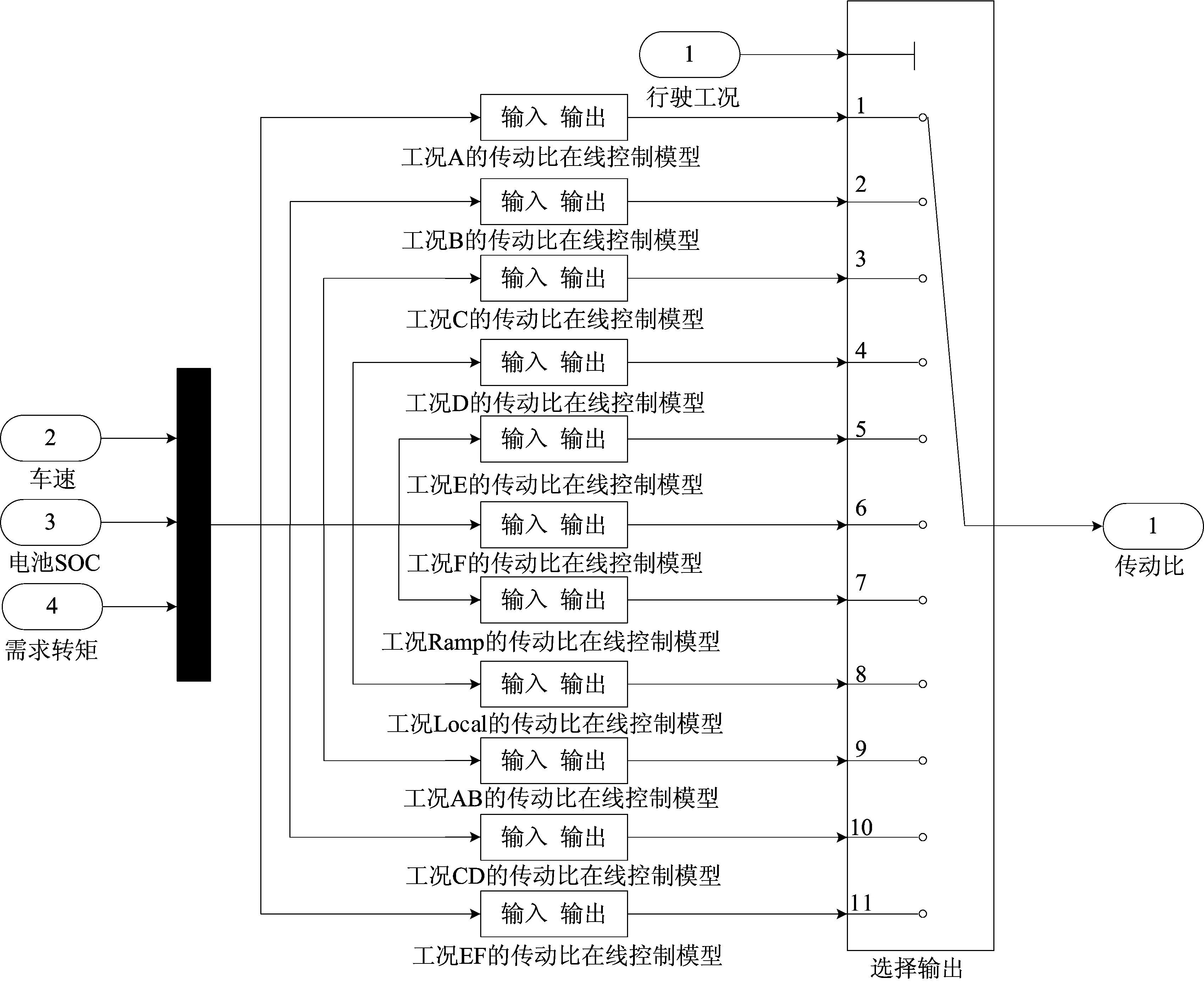
(b) 传动比在线控制模型图6 在线控制模型

其中,电机转矩在线控制模型的输入为行驶工况、车速、电池SOC、需求转矩、行驶模式和传动比;传动比在线控制模型的输入为行驶工况、车速、电池SOC和需求转矩。

4.2 基于离线最优轨迹的综合在线控制策略

将建立的行驶特征预测模型与电机转矩、传动比在线控制模型相结合,设计了基于行驶特征预测及离线最优轨迹的综合在线能量管理策略,以实现在汽车实际行驶中对动力系统能量的实时优化分配。本文在线控制策略示意图如图7所示。

在线控制策略下,当车辆开始运行时，工况类别预测模型会预测下一阶段的工况类别,行驶模式预测模型会预测短期内的行驶模式,从而触发相应行驶状态下的电机在线控制模型和传动比在线控制模型,进而实时地合理分配发动机与电机之间的动力,满足驾驶需求、提高能量利用率,从而降低油耗。

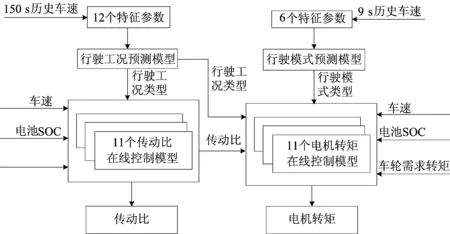
图7 在线控制策略示意图

5 仿真及结果分析

将本文设计的Simulink综合在线控制策略模型嵌入到ADVISOR整车模型中,采用构造的组合车辆行驶工况(NEDC+HWFET+UDDS+LA92)进行控制策略的合理性检验,仿真结果如图8所示。因为仿真测试工况的时间较长,在整个测试工况下行驶模式和传动比变化较多,所以只给出了部分测试工况的行驶模式和传动比分配图,如图8c、图8d;图8f中,在线策略指本文设计的综合在线控制策略,电机辅助指基于规则的电机辅助控制策略。

从图8a可以看出,制定的综合在线控制策略进行仿真时,工况跟随状况良好。

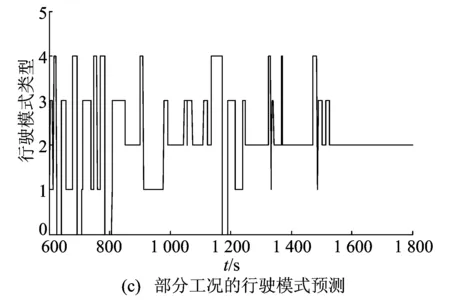
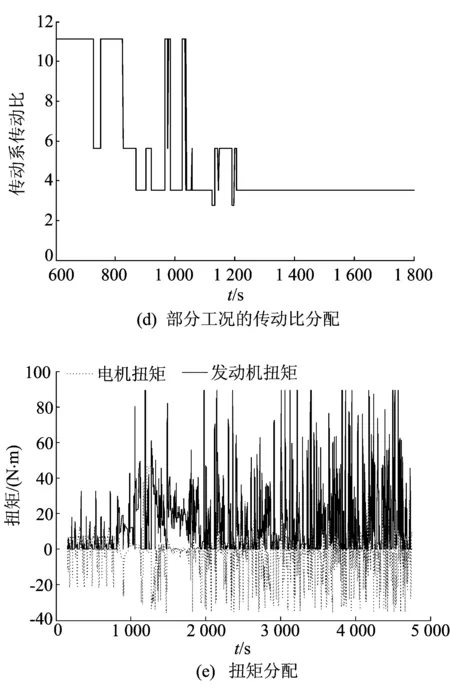
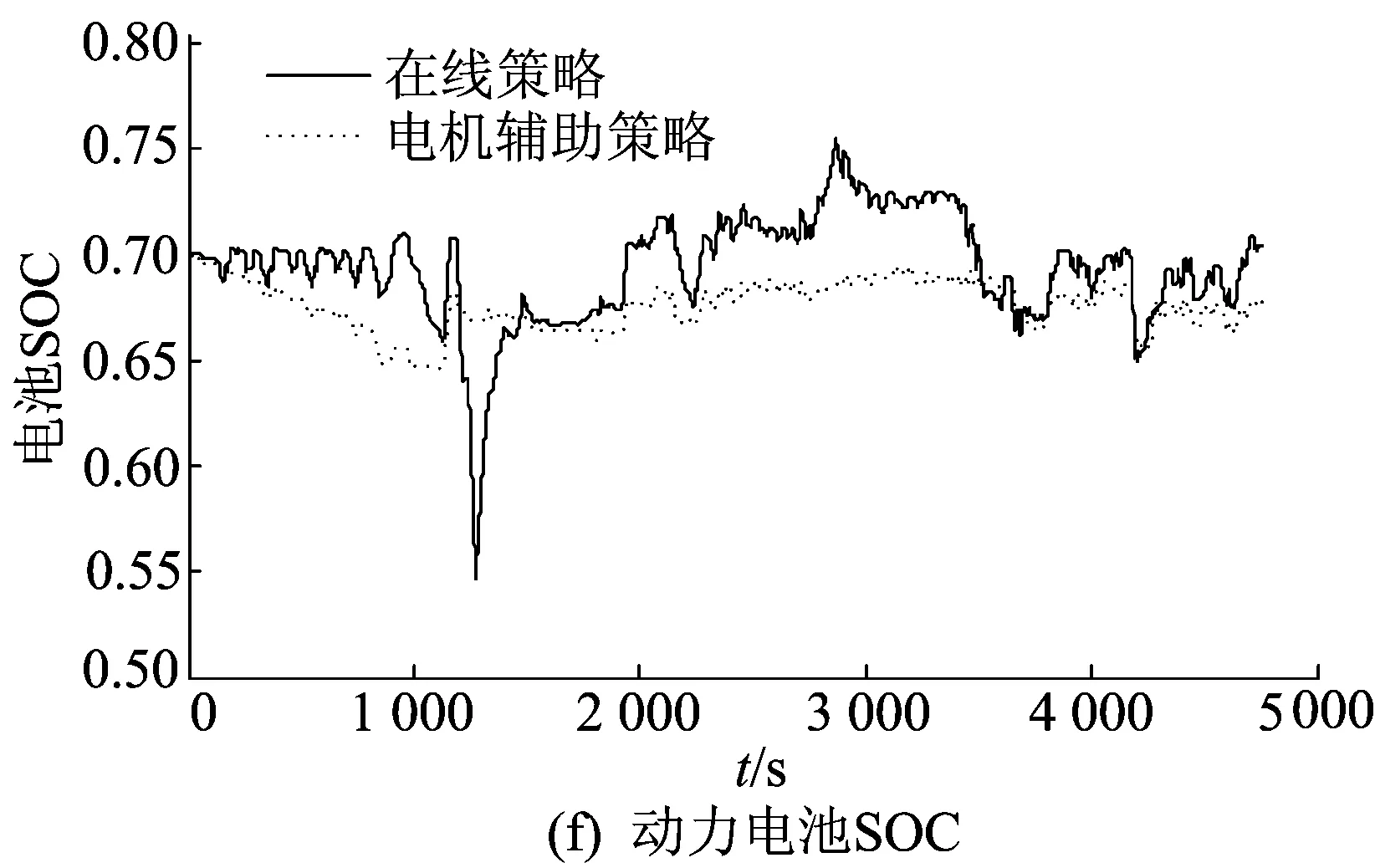
图8仿真结果

由图8b～图8d可知,制定的行驶工况预测方法、行驶模式预测结果和传动比的分配均较合理,达到了预期效果。

由图8e可知,本文控制策略的需求转矩分配较合理，在拥堵工况和城市工况(3 000～3 500 s)电机能主动回收能量;在郊区工况和高速路工况(1 500 ～ 1 800 s)车辆能更好地协调电机和发动机之间的转矩分配,充分发挥了电机的辅助驱动作用。

从图8f可以看出,在1 300 s附近电池SOC曲线迅速下降,这是由于此时车辆急加速,其需求功率突然增大,电机立即开始工作,而后发动机迅速启动并工作于其最大转矩附近,为车辆提供动力的同时也给蓄电池充电,从而电池SOC开始回升;另外,电池SOC末值回到0.70,相比于基于规则的电机辅助控制策略 SOC末值的0.68,更接近动态规划的结果,说明本文所设计的策略电池电量保持能力更好。

对于选用的组合测试工况,2种控制策略的仿真初始SOC值均为0.70,基于规则的电机辅助控制策略油耗为每百公里3.40 L,SOC末值为0.68;而在线控制策略油耗为每百公里3.20 L,SOC末值为0.70。电池SOC通过插值拟合修正之后[16],2种策略的油耗分别为每百公里3.46、3.20 L,油耗下降了7.51%。

综上所述,采用本文在线控制策略能够根据行驶特征的变化,实时地调整HEV各动力源的扭矩分配,同时在保证电池荷电状态平衡的基础上,使发动机工作在高效率区,从而达到降低汽车燃油消耗的目的。

6 结 论

本文基于DP理论研究了全局最优控制策略;根据车辆行驶特征对HEV燃油经济性的影响,提出了HEV行驶特征预测方法;将车辆的行驶特征预测与全局最优控制策略相结合,以整车燃油经济性为目标,同时兼顾电池SOC平衡,实现了全局最优策略的在线应用;最后在Matlab/Simulink平台上进行策略验证,证实了本文制定的在线控制策略在保证电池SOC平衡和燃油经济性方面都有较优的表现。

后续的研究工作是将控制策略应用于实车道路试验中，根据试验结果控制策略进行改进。