基于DSP的数控机床在机测量系统测量误差实时建模预测

杨洪涛, 顾嘉辉, 江 磊, 庞勇军, 李 莉

(安徽理工大学 机械工程学院,安徽 淮南 232001)

0 引 言

数控机床在机测量系统的测量主要是依靠机床本体和测头实现的,其中机床XY工作台的定位误差是影响测量精度的关键来源之一,其受测量坐标位置、运动速度、各部件的装配精度、摩擦磨损等因素的影响。近年来不少学者对XY工作台定位误差建模补偿方法开展研究,常用的误差建模方法有最小二乘法、多体系统理论、齐次坐标变换法、正交多项式等[1-4]。但通过上述方法建模必须利用误差预测软件实现补偿,存在误差影响因素考虑不足、误差预测模型复杂、补偿实时性差的问题。数字信号处理器(digital signal processor,DSP)是一款能利用硬件实现复杂算法运算的微处理器,片上整合了多种外设,具有强大的控制能力和运算能力,多应用于处理速度和精度要求高的领域。国内外学者经常将复杂算法植入DSP中,实现对物理量的实时检测和误差补偿。文献[5]将反向传播 (back propagation,BP)神经网络植入DSP用于旋转机械在线故障诊断;文献[6]将模糊PID算法植入DSP中,实现了伺服电机速度的实时补偿。

为了提高数控机床在机测量系统的测量误差补偿效果,本文提出一种利用遗传算法(genetic algorithm,GA)优化BP神经网络并考虑坐标位置、运动速度的机床XY工作台定位误差建模方法,利用DSP硬件系统实现误差的精确预测补偿。

1 XY工作台定位误差分析与建模

数控机床在机测量系统由数控机床本体和测头组成,两者的误差都会影响测量系统的测量精度,其中XY工作台的定位误差是影响机床误差的主要来源,而且受到运动坐标位置、运动速度等影响,变化规律复杂,因此本文主要开展XY工作台的定位误差实时补偿。

1.1 XY工作台的定位误差分析

数控机床XY工作台结构如图1所示,由工作台面、伺服电机、联轴器、滚珠丝杠、光栅、导轨和支撑轴承构成。

由伺服电机通过联轴器带动滚珠丝杆旋转,从而带动丝杠螺母副和工作台面做直线运动,通过光栅测量显示其运动位置。XY工作台运动定位误差主要来源于导轨系统几何误差、滚珠丝杠的螺距误差以及光栅测量系统的零位与示值误差。这些误差受到工作台运动坐标和速度的影响,变化规律复杂,存在相关性,难以建立白化模型,因此本文采用GA算法优化的BP神经网络对其定位误差建模。

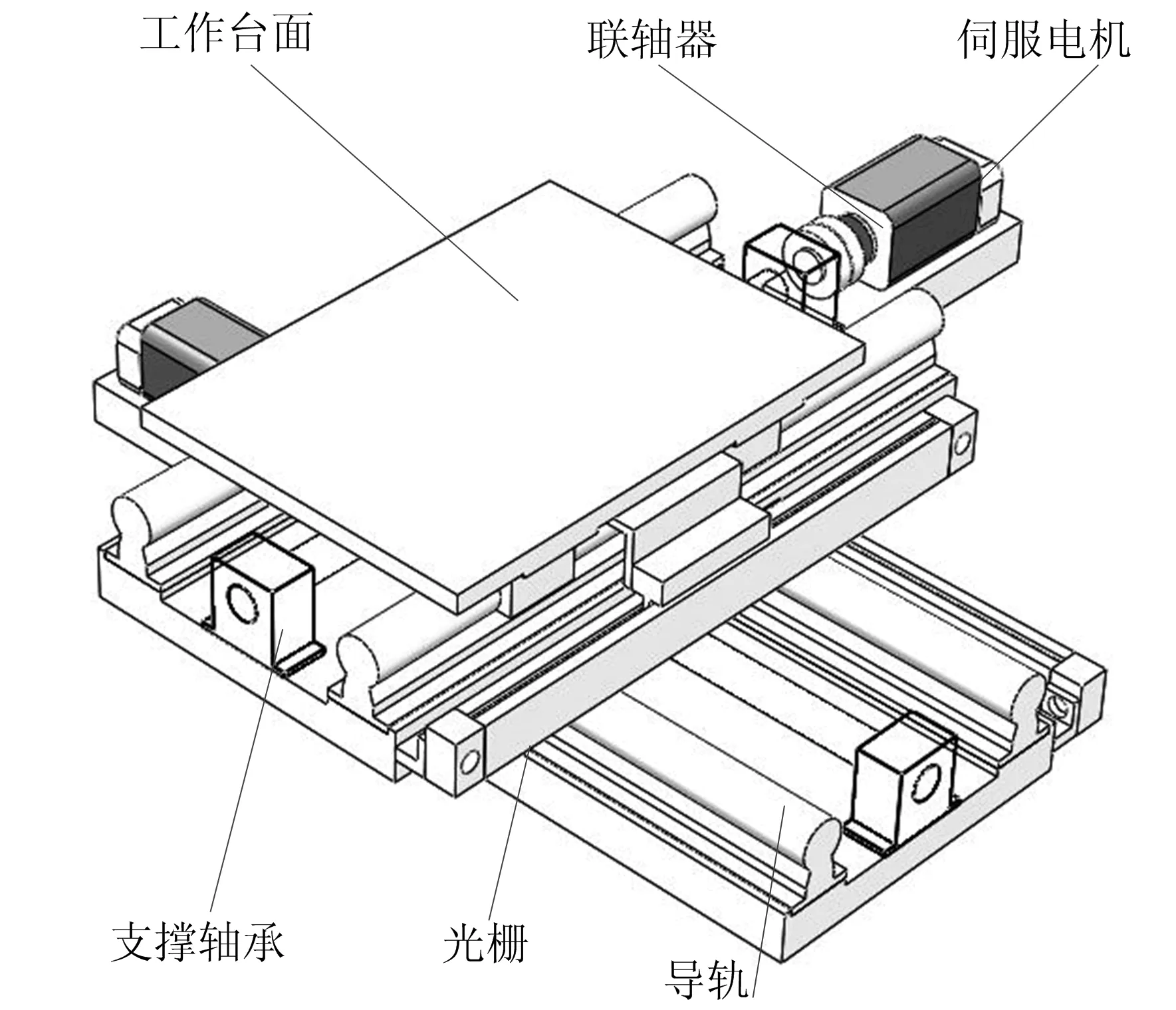
图1 数控机床XY工作台

1.2 定位误差建模

将不同p值代入神经网络模型,经过多次比较建模效果,得到p取6时残差平方和最小,即预测精度最高,因此建立GA-BP神经网络结构为2-6-1,如图2所示。

利用GA算法优化的BP神经网络算法流程如图3所示。

首先建立BP神经网络拓扑结构,输入相关参数(定位位置、运动速度等),对数据预处理后产生初始种群,经过选择、交叉、变异等GA算法操作获得最优的权值和阈值,最后根据最优权值和阈值获得最优的BP神经网络结构[7-8]。

图2 GA-BP神经网络拓扑结构>

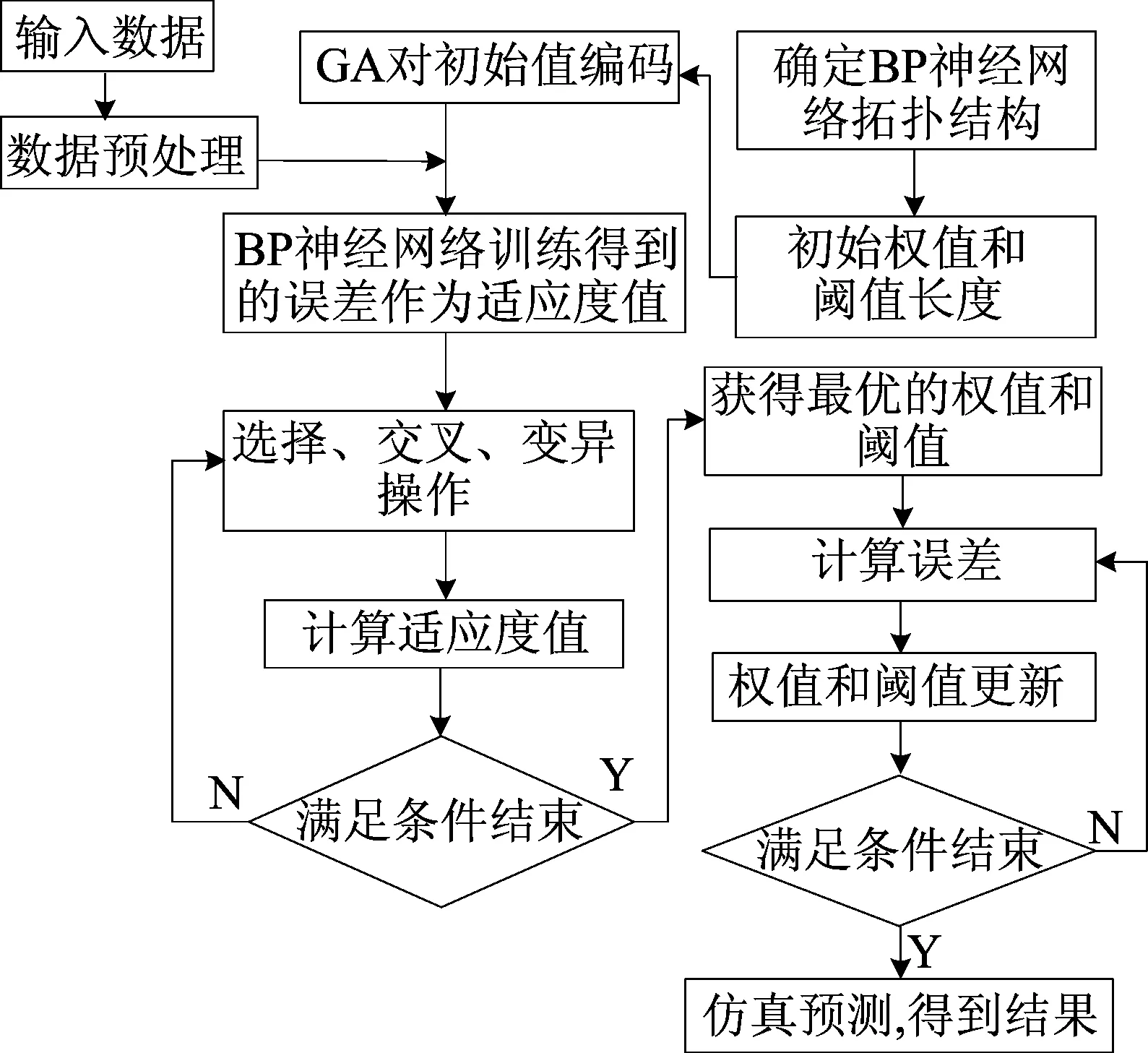
图3 GA-BP神经网络算法流程

2 定位误差建模预测系统硬件设计

为了提高数控机床在机测量系统定位误差预测补偿的实时性和精度,本文选择型号为TMS320F28335DSP芯片进行设计XY工作台定位误差的建模预测系统。

2.1 系统工作原理及硬件组成

本文采用的TMS320F28335 DSP是一款支持高性能集成外设的32位微控制器,主频达到150 MHz,片上集成了ADC、PWM、SCI、CAN、MCBSP、I2C等多种常用外设,适用于实时控制应用[9]。

本文定位误差建模预测补偿系统由数控系统进给轴反馈装置、DSP建模预测系统和数控系统控制器组成,如图4所示,其中电源电路、复位电路、时钟电路、JTAG电路构成了DSP的最小系统。定位误差预测补偿采用反馈中断式补偿方法,将DSP模块预测的误差嵌入到数控机床伺服系统的光栅位置反馈环节实现补偿[10]。通过DSP与机床数控系统通信,获取位置坐标、速度信号,输入应用DSP的定位误差建模预测系统,将预测得到的定位误差转换为补偿的脉冲信号添加到伺服系统的反馈环中实现补偿。

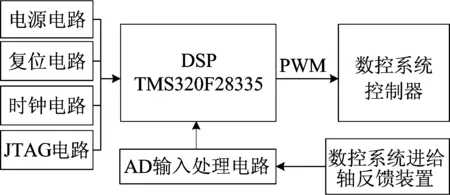
图4 定位误差预测补偿系统硬件组成

3 定位误差建模预测系统软件设计

首先利用Matlab建立GA-BP模型,获得优化后的权值和阈值,然后移植到DSP中进行建模、预测,能大大提高预测速度。

3.1 Matlab建模

本文建立的BP神经网络采用3层网络结构,隐含层和输出层的传递函数分别采用tansig、purelin,训练函数选用trainlm,具体参数设置为训练次数2 000次、学习速率0.1、训练目标0.001;利用GA算法优化BP神经网络定位误差预测模型初始权值和阈值时,GA算法的的参数设置为种群规模80、遗传代数50、交叉概率0.8、变异概率0.05。由此在Matlab中建立GA-BP模型。

3.2 DSP实现GA-BP神经网络

将Matlab中建立的GA-BP模型进行训练,得到优化的权值和阈值,并在DSP中建模,其流程如图5所示。

首先将输入数据初始化(归一化);其次根据公式建立GA-BP模型,将初始化的数据代入模型预测;最后将预测数据处理(反归一化)后输出。整个程序所涉及的数学描述如下。

由GA-BP神经网络的网络结构可知,输入层到隐含层的函数为:

(1)

隐含层到输出层的函数为:

purelin(n)=n

(2)

因此输出层输出为:

y=purelin[w2tansig(w1x+b1)+b2]

(3)

其中,w1、w2分别为输入层到隐含层以及隐含层到输出层的权值;b1、b2分别为输入层到隐含层以及隐含层到输出层的阈值;x为输入变量;y为输出值。

神经网络运算时涉及到归一化问题,因此需要建立归一化函数和反归一化函数,tansig(n)函数的值域为(-1,1),建立归一化函数如下:

(4)

其中,t为原值,为归一化值;amax为数据最大值;amin为数据最小值。

反归一化函数为:

(5)

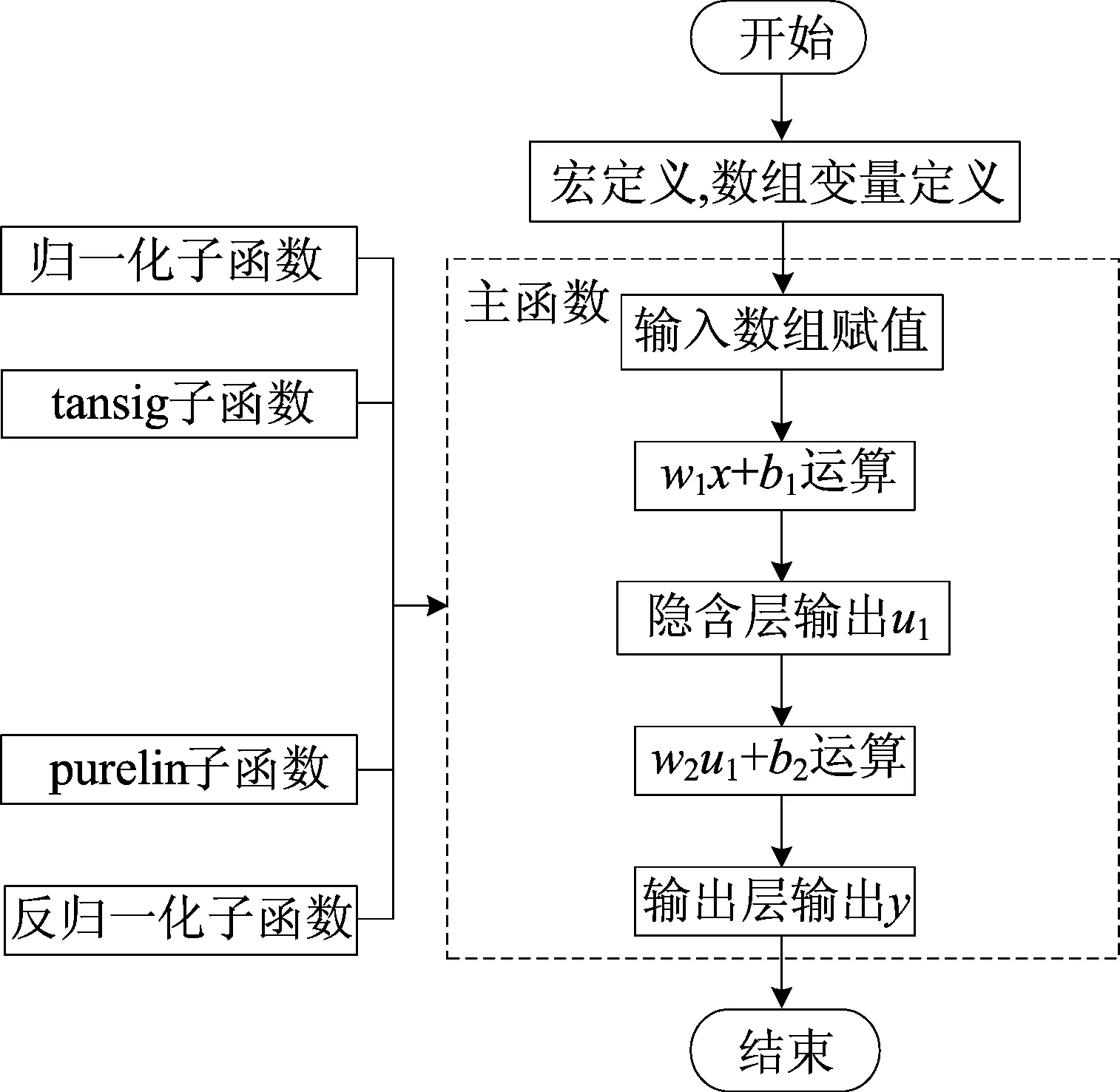
图5 DSP程序流程

4 实验验证

4.1 实验装置与实验方案设计

本文设计的实验装置如图6a所示,该装置由XY工作台、数控装置、激光干涉仪组成。由数控装置控制工作台运动速度,利用激光干涉仪采集XY工作台在X方向运动的定位误差。工作台运动速度分别设置为1.0、1.5、2.0、2.5、3.0、4.0、6.0、8.0 mm/s,其行程为0～150 mm。激光干涉仪每隔5 mm采集1次定位误差数据,在相同运动速度、位置下重复采集3组,求平均值,共得到248个数据,如图6b所示。从图6b可以看出,工作台在不同空间位置、运动速度下的定位误差不同,变化规律复杂。

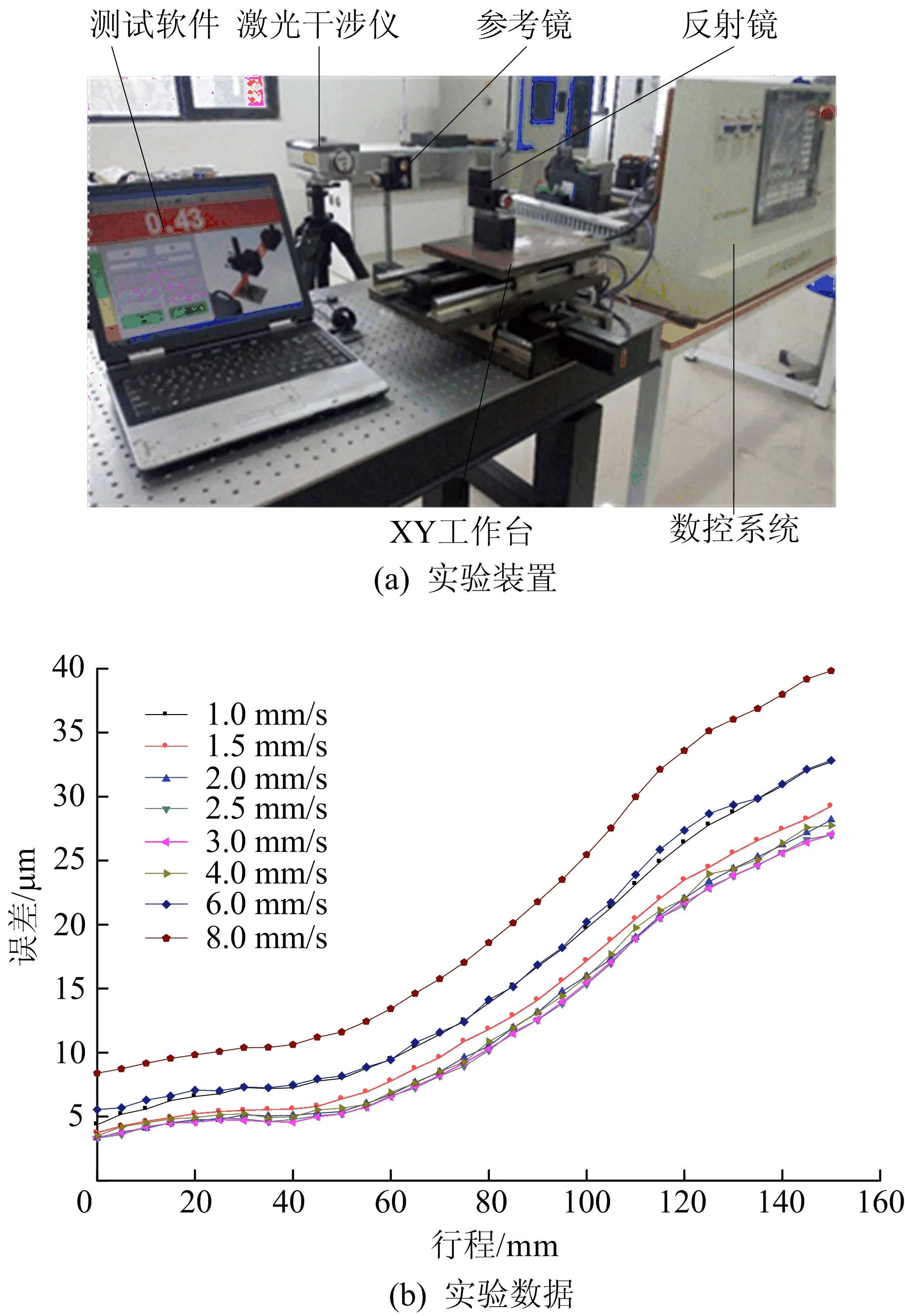
图6 实验装置与实验数据

4.2 BP和GA-BP神经网络预测对比

本文分别利用GA-BP神经网络模型和BP神经网络模型进行定位误差建模,比较两者的建模预测精度。将速度6 mm/s、位置0～150 mm的定位误差数据预留为验证数据,在其他7种运动速度下的工作台全行程定位误差数据作为训练数据。把训练数据代入2种神经网络中训练,分别建立基于BP神经网络和GA-BP神经网络的定位误差预测模型。将速度和位置坐标输入到所建立的预测模型,预测得到的工作台定位误差、激光干涉仪测量得到的实际定位误差、建模预测误差如图7所示。从图7可以看出,GA-BP神经网络建模预测模型的预测精度更高。

为了比较利用Matlab和DSP建立的预测系统的实时性和预测精度,分别利用2种预测系统进行工作台定位误差的预测比较。将权值和阈值训练优化后的GA-BP神经网络分别利用Matlab和DSP进行运行,比较其预测时间和数据残差。利用Matlab软件运行的优化权值和阈值后的GA-BP神经网络,预测31个误差所需时间为249 μs;而利用DSP建立的预测系统预测每个误差时间为29.6 μs,预测31个误差所需时间为914.1 μs。利用DSP建立的预测系统预测每个定位误差残差分布为-0.688 190～0.512 744 μm(图7b)。虽然Matlab的预测时间略优于DSP，但Matlab适用于电脑端算法模拟，实现后期补偿还需添加外围软硬件，且实现方式繁琐；而DSP集成多种片内外设，可扩展性强，且预测时间可以满足数控机床在机测量系统定位误差补偿的要求。

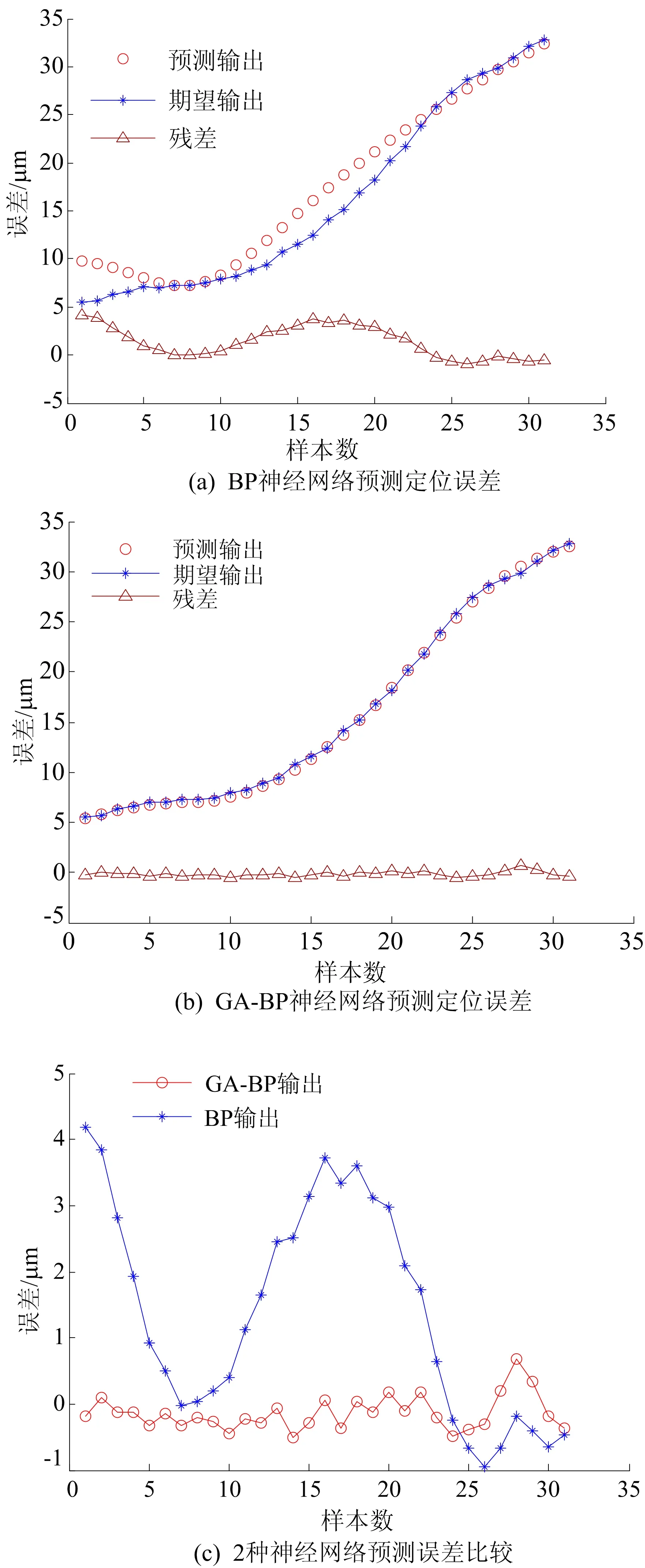
图7 GA-BP与BP神经网络预测定位误差的比较

5 结 论

(1) 本文分析了数控机床在机测量系统XY工作台定位误差的影响因素及特点,通过GA-BP神经网络方法建立了XY工作台定位误差预测模型。

(2) 设计了基于DSP的XY工作台定位误差建模预测补偿系统,介绍了其硬件组成和软件工作流程。

(3) 对设计的基于DSP的XY工作台定位误差建模预测补偿系统进行实验验证与比较。由实验结果可知,相比于BP神经网络建立的误差预测模型,利用GA-BP神经网络建立的定位误差预测模型预测精度更高、鲁棒性更好。利用DSP硬件系统预测每个误差运行时间为29.6 μs,残差分布为-0.688 190～0.512 744 μm,可以用于数控机床在机测量系统其他组成部分和综合测量误差的实时补偿以及误差补偿器的实现。