大规模MIMO系统中基于梯度投影的混合波束赋形算法

李民政， 王 浩

(1.桂林电子科技大学 计算机与信息安全学院，广西 桂林 541004; 2.上海电机学院 电子信息学院，上海 201306)

混合波束赋形结合模拟波束赋形和基带数字波束赋形，能够减少完全数字波束赋形所需的射频链数量[1]，并尽可能地接近完全数字波束赋形的频谱效率性能。因此，混合波束赋形在毫米波大规模多输入多输出通信系统中引起了广泛关注[2]。文献[3]考虑了具有正交频分复用的宽带系统下的混合波束赋形设计，将频率选择性信道的模拟波束赋形设计转换为平坦衰落信道的模拟波束赋形设计。文献[4]采用基于坐标下降的交替最小化算法获得混合的数字和模拟波束赋形，并证明在低分辨率移相器下能获得最优的性能。在多用户信道模型下，文献[5]采用一种分层码本训练方法来设计混合波束赋形，然而码本的大小总是随着天线的数量线性地甚至指数地增加，造成模拟波束的搜索是复杂的。文献[6]提出了一种新的迭代算法，在干扰信道中用干扰对齐方案来最大化频谱效率，但迭代收敛速度慢。文献[7]研究了基于最小均方误差标准下多用户毫米波通信系统的混合模拟和数字波束赋形设计。文献[8]利用惩罚双重分解方法解决毫米波多用户MIMO系统的非凸混合波束赋形问题，同时可以保证PDD方法的收敛性。文献[9]考虑最优的用户组合和功率分配，将求解混合波束赋形的非凸约束问题转换为凸半正定问题。上述研究关注的重点是毫米波通信下的混合波束赋形设计时的最大化系统频谱效率，而很少关注混合波束赋形设计时如何降低算法的计算复杂度。

在毫米波Massive MIMO下行通信系统中，先改进一种基于Neumann级数近似求逆的块对角波束赋形算法获得完全数字波束赋形，然后在设计混合波束赋形时，使用交替最小化算法作为确定混合数字波束和模拟波束赋形的主要设计原则，在模拟波束赋形设计上提出一种改进的梯度投影算法，能够解决计算复杂度高的问题，且保证和速率受损较少。

1 系统模型

图1 毫米波MIMO系统框图

假定毫米波信道为几何信道模型[1]，其中第k个用户的下行链路信道为

(1)

at(θk,l)=

(2)

ar(φk,l)=

(3)

第k个用户接收的信号为

(4)

(5)

其中，

2 混合波束赋形算法

2.1 完全数字波束赋型

多用户下的信道矩阵表示为

(6)

对应于第k个用户的干扰矩阵为

(7)

B=[B1,B2,…,BK]。

(8)

基于SVD的块对角完全数字波束赋形算法需要奇异值分解，具有高计算复杂度。为了降低计算复杂度，采用Neumann级数近似求逆的方法来代替奇异值分解。由文献[10]可知，完全数字波束赋形矩阵可表示为

B=HH(HHH)-1M。

(9)

假定P=HHH，T=IM-βP，β为满足引理的参数，则有

(10)

其中：L为矩阵多项式的阶数；αn为多项式系数，可表示为α=[α1,α2,…,αL]T。

求解最优的β和α可表述为式(11)的优化问题[12]，求解β和α即可求解P-1。

(11)

其中ρr(·)为矩阵谱半径。

以上过程的具体步骤如下：

1)输入矩阵H，根据式(10)、(11)计算(HHH)-1；

2)对于每个用户，

Mk=Uk(:,1:sr)Σk(1:sr,1:sr)-1/2；

3)输出完全数字波束赋形矩阵，

B=HH(HHH)-1M。

在求解(HHH)-1时，β和α是预先求出，所以计算复杂度仅在多项式矩阵相乘。一般用Neumann series级数的前3项即可近似表示逆矩阵，复杂度为(KNr)3+Nt(KNr)2+KNtNr。与基于SVD和直接矩阵求逆的方法相比，采用多项式矩阵相乘代替，避免了矩阵SVD和求逆，可以有效减少计算复杂度。

2.2 混合波束赋形

由文献[13]可知，求得完全数字波束赋形矩阵后，基站最优模拟波束赋形矩阵A和数字波束赋形矩阵D求解可以表述为

(12)

其中D=[D1,D2,…,DK]。

采用交替最小算法分别求解最优模拟波束赋形矩阵A和数字波束赋形矩阵D，即对于任意初始化矩阵A(p)，从p=0开始，并对每个迭代p执行：

(13)

(14)

2.3 模拟波束赋形

假设移相器是连续的，应用Frobenius范数表示目标函数[14]

f(x)≜‖u-Gx‖2，

向量u≜vec(B)∈CV×1，向量x≜vec(A)∈CU×1和矩阵

G≜(D(p+1))T⊗INt∈CV×U，

(15)

文献[14]采用流形优化(manifold optimization，简称MO)共轭梯度算法求解式(15)的优化解，其求解过程中需要计算欧几里德共轭梯度、投影梯度到切线空间、搜索切线空间中的点等运算步骤，涉及大量矩阵乘法运算，算法复杂度较高。

通常在梯度投影算法中求解搜索步长μ涉及矩阵奇异值分解，为了避免奇异值分解计算，设置μ=ωτ,ω∈(0,1)，文献[15]已证明只要保证μ小于或等于Lipschitz常数ζ，投影梯度算法将会收敛到Karush-Kuhn-Tucker点，τ为由文献[16]推导出的边界，

(16)

其中，r1,r2,…,rU为G的行和。

以上过程的具体步骤如下：

1)输入B,D(p+1)，将矩阵B向量化，即u=vec(B)；

3)计算投影矩阵G=(D(p+1))T⊗INt；

2.4 复杂度比较

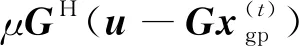
3 仿真结果与分析

仿真环境中相应阐述设置如下：基站发射天线数Nt=128，每个用户的接收天线数Nr=32，用户数K=4，发射角与到达角均匀分布在[0,2π]内，基站天线间隔d=λ/2，每个用户的数据流sr=4，基站的数据流st=Ksr，总发射功率P=Ksr，基站与每个用户间的散射路径Lk=8。

图2为基于奇异值分解的块对角波束赋形算法和提出的基于Neumann级数近似求逆的算法求解完全数字波束赋形的和速率性能对比。从图2可看出，本算法的和速率接近基于奇异值分解的算法。由于采用基于Neumann级数近似求逆代替奇异值分解，与基于奇异值分解的算法相比，具有较低的计算复杂度。

图2 2种完全数字波束赋形算法的和速率对比

图3为在混合波束赋形设计中提出的梯度投影算法在不同迭代次数下和速率变换曲线。从图3可看出，本算法能快速收敛，仅在T=2时，便很接近最优全数字波束赋形的性能。之后随着迭代次数增加，性能有所提升，但也提升不大。为了便于与流形优化算法比较及体现性能优势，在仿真中本算法设置T=10。

图4 不同算法下和速率对比

图5为在信噪比RSN=0和RSN=10 dB下，射频链数为3～8时的用户和速率变换曲线。从图5可看出，随着射频链数增加，本算法的用户和速率不断接近完全数字波束赋形,且与MO算法的性能基本保持相同。

图5 不同射频链下和速率变换曲线

4 结束语

在多用户毫米波MIMO下行无线通信系统中，针对完全数字波束赋形和混合波束赋形设计的高计算复杂度，先改进一种低复杂度的完全数字波束赋形算法，然后基于交替最小化算法设计混合波束赋形矩阵，提出一种基于梯度投影的算法来确定模拟波束赋形，在保证和速率性能损失较少的情况下，降低了计算复杂度。