Stiefel流形约束下矩阵迹函数最小化问题的黎曼共轭梯度算法

秦树娟， 周学林， 李姣芬

(1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004； 2.桂林电子科技大学 教务处，广西 桂林 541004)

流形约束优化问题作为数值领域的一个活跃研究课题，一直以来备受关注，其基本迭代式为

(1)

问题1给定矩阵X∈Rn×m，F，D∈Rn×n及正则化参数α，给定非凸约束集合

St(m,d)={Q∈Rm×d:QTQ=Id}，

求Q∈St(m,d)，P∈Rd×m，使得

PTQTXTDXQP+αPTP),

s.t.QTQ=I,P∈Rd×m。

(2)

其中可行集

St(m,d)={Q∈Rm×d:QTQ=Id}，

当d≤m时，称其为Stiefel流形。

令

f(Q,P)=tr(XTDX-2PTQTXTFX+

PTQTXTDXQP+αPTP)，

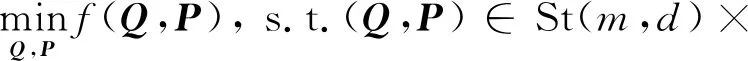
(3)

1 预备知识

1.1 St(m,d)×的切空间、正交投影及目标函数f(Q,P)的黎曼梯度

TQSt(m,d)={ξ∈Rm×d:ξTQ+QTξ=0};

(4)

(5)

(6)

令在欧式空间Rm×d×Rd×m上赋有如下标准内积：

(X1,Y1),(X2,Y2)∈Rm×d×Rd×m。

〈(ξ1,η1),(ξ2,η2)〉(Q,P)=〈(ξ1,η1),(ξ2,η2)〉,

ΓQξ=ξ-Qsym(QTξ)；

(7)

ΓPη=η。

(8)

Γ(Q,P)(ξ,η)=(ΓQξ,ΓPη)。

(9)

通过f(Q,P)对Q，P分别求导，可得其在Q，P处的欧式梯度：

(XTDTXQPPT+XTDXQPPT)=

XT(DT+D)XQPPT-2XTFXPT；

(QTXTDXQP+QTXTDTXQP)+2αP=

2(αP-QTXTFX)+QTXT(DT+D)XQP。

Gf(Q,P)=(GQf(Q,P),GPf(Q,P))。

gradf(Q,P)=Γ(Q,P)Gf(Q,P)=

(ΓQGQf(Q,P),ΓPGPf(Q,P))。

(10)

1.2 收缩算子和向量转移算子

命题1令Q∈St(m,d)，W∈Rm×m为反对称矩阵，若定义集合

ΩQ={ξ∈Rm×d|ξ=WQ}，

则有ΩQ=TQSt(m,d)。

证明令ξ∈TQSt(m,d)，定义反对称矩阵

Wξ=PQξQT-QξTPQ,

且

由式(4)可知，

ξTQ=-QTξ，

可得

WξQ=PQξ-QξTPQQ=

于是有TQSt(m,d)⊂ΩQ。令ξ∈ΩQ，存在一个反对称矩阵W∈Rm×m,使得ξ=WQ，则有

ξTQ+QTξ=(WQ)TQ+QTWQ=

-QTWQ+QTWQ=0，

于是有ΩQ⊂TQSt(m,d)。综上可知，

TQSt(m,d)=ΩQ。

对∀Q∈St(m,d)，采用拟测地线中的一类由凯莱变换构建的收缩算子：

ξ∈TQSt(m,d)，

(11)

其中：

Wξ=PQξQT-QξTPQ，

且ξ=WξQ由命题1可得。

(12)

R(Q,P)(α(ξ,η))=(RQ(αξ),RP(αη)),

(13)

(14)

采用由微分收缩算子的向量转移算子

(15)

则Stiefel流形上的向量转移算子为

(16)

式(16)满足如下的Ring-Wirth非扩张条件[6]：

〈Ταη(η),Ταη(η)〉R(αη)≤〈η,η〉。

(17)

因式(16)涉及m×m阶逆矩阵的计算，当m≥2d时，其计算量较大，故也可采用降阶的方法来减少计算量[6]。以下仅给出其降为2d×2d阶逆矩阵时的计算式：

(18)

其中：

M1=VΤQ,M2=VΤU,

且当m≤2d时，仍应选用式(16)。

Ταη(η)=η。

(19)

Τα(ξ,η)(ξ,η)=(Ταξ(ξ),Ταη(η)),

(20)

2 求解问题(3)的黎曼共轭梯度法

Dai的非单调共轭梯度法[7]中迭代参数βk+1为

其中yk=gradf(Xk+1)-gradf(Xk), 将其推广至黎曼流形上，则有

(21)

其中，

Yk+1=〈gradf(Qk+1,Pk+1),Ταk(ξk,ηk)(ξk,ηk)〉-

〈gradf(Qk,Pk),(ξk,ηk)〉。

为保证算法的全局收敛性，采用Armijo型非单调线性搜索条件，其黎曼概括为

f(R(Qk,Pk)(αk(ξk,ηk))≤max{f(Qk,Pk),

f(Qk-1,Pk-1),…,f(Qk-m(k),Pk-m(k))}+

δαk〈gradf(Qk,Pk),(ξk,ηk)〉,

其中m(k)=min{m-1，WK}。

算法11) 给定初值

选取参数ε,δ,λ∈(0,1)，m∈N+，步长αmax>α0>αmin>0，令

(ξ0,η0)=-gradf(Q0,P0)，k=0。

2) 当‖gradf(Qk,Pk)‖>ε时，进行下一步。

3) 若步长αk满足

f(R(Qk,Pk)(αk(ξk,ηk)))≤max{f(Qk,Pk),

f(Qk-1,Pk-1),…,f(Qk-m(k),Pk-m(k))}+

δαk〈gradf(Qk,Pk),(ξk,ηk)〉，

(22)

则转步骤4)，否则，转步骤5)。

4)令(Qk+1,Pk+1)=R(Qk,Pk)(αk(ξk,ηk))，R由式(11)定义，若m≥2d则由式(14)定义。

5) 令αk=λαk，转步骤3)。

6) 计算

(ξk+1,ηk+1)=-gradf(Qk+1,Pk+1)+

βk+1Ταk(ξk,ηk)(ξk,ηk)，

(23)

7) 更新αk+1∈[αmin,αmax]，并令k=k+1。

3 收敛性分析

Ψ:=

{(Q,P)∈St(m,d)×Ρ|f(Q,P)≤f(Q0,P0)}

(24)

是紧集。

T(Q,P)St(m,d)×⊂Rm×d×Rd×m，

故gradf(Q,P)可看作

的连续映射。因此，对任意点，

gradf(Q2,P2)-gradf(Q1,P1)

是存在的。由引理2可知， gradf(Q,P)在Ψ上是Lipschitzian连续的，即

∀(Q1,P1),(Q2,P2)∈Ψ，

存在一个Lipschitzian常数L>0,使得

‖gradf(Q1,P1)-gradf(Q2,P2)‖≤

Ldist((Q1,P1)-(Q2,P2)),

(25)

引理3[6]假设算法1未在有限步迭代后终止，则对任意的k，有

〈gradf(Qk,Pk),ηk〉<0。

(26)

〈gradf(Qk+1,Pk+1),(ξk+1,ηk+1)〉=

‖gradf(Qk+1,Pk+1)‖2。

(27)

若令

〈gradf(Qk+1,Pk+1),Ταk(ξk,ηk)(ξk,ηk)〉≥0，

则由归纳假设知

Yk+1=〈gradf(Qk+1,Pk+1),Ταk(ξk,ηk)(ξk,ηk)〉-

〈gradf(Qk,Pk),(ξk,ηk)〉>0，

则有

〈gradf(Qk+1,Pk+1),(ξk+1,ηk+1)〉=

‖gradf(Qk+1,Pk+1)‖2，

于是

〈gradf(Qk+1,Pk+1),(ξk+1,ηk+1)〉<0。

若令

〈gradf(Qk+1,Pk+1),Ταk(ξk,ηk)(ξk,ηk)〉<0，

则有

〈gradf(Qk+1,Pk+1),(ξk+1,ηk+1)〉=

‖gradf(Qk+1,Pk+1)‖2，

于是同样有

〈gradf(Qk+1,Pk+1),(ξk+1,ηk+1)〉<0，

故对k+1而言，式(26)也成立。因此，对任意的k，式(26)都成立。

引理4[9]对算法 1，存在一个正常数μ>0,使得对任意的k都有

(28)

(29)

定理1假设算法 1在有限步迭代后未终止，则由该算法产生的序列在以下条件下收敛：

(30)

因此至少存在一个一阶临界点的聚点。.

‖gradf(Qk,Pk)‖≥γ,∀k,

(31)

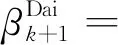
其中，

Δk+1=(1-rk+1)〈gradf(Qk+1,Pk+1),

Ταk(ξk,ηk)(ξk,ηk)〉,-rk+1×

〈gradf(Qk+1,Pk+1),Ταk(ξk,ηk)(ξk,ηk)〉，

结合引理3有

(32)

由式(23)可知,

‖(ξk+1,ηk+1)‖2=-2〈gradf(Qk+1,Pk+1),

(ξk+1,ηk+1)〉-‖gradf(Qk+1,Pk+1)‖2+

(33)

式 (33)两边同除

〈gradf(Qk+1,Pk+1),(ξk+1,ηk+1)〉2,

并结合式(32)、(17)可得，

(34)

由式(34)、式(31)可知，

(35)

于是

(36)

另一方面，由式(34)、(35)可知，

于是

(ξk,ηk)〉+‖gradf(Qk,Pk)‖2。

(37)

若

则根据式(37)有

因此，由引理3和式(31)知，

(38)

〈gradf(Qmj+i-2,Pmj+i-2),(ξmj+i-2,ηmj+i-2)〉,μ×

而这与式(29)相矛盾，因此式(31)不成立，从而可知式 (30)成立。

4 结束语

针对机器学习特征提取中的一类Stiefel流形约束下矩阵迹函数问题，先将其转化为乘积流形约束下的最小化问题，再采用带有Armijo型非单调线性搜索的黎曼共轭梯度算法对其进行求解，并给出了该方法的全局收敛性证明。