基于多项式拟合和多普勒周跳探测与修复

赵松克， 付文涛， 阮兰君

(桂林电子科技大学 广西精密导航技术与应用重点实验室,广西 桂林 541004)

周跳问题广泛存在于卫星导航定位等工程测量中，会破坏卫星至接收机的距离观测值的变化规律，对定位产生影响。一直以来，提出有效且实用的周跳探测方法是载波相位数据处理中周跳探测的难点。只有有效地探测出周跳，才能保证载波相位周跳修复以及整周模糊度固定的精确性。

在载波相位观测方程中，由于测量误差和模型误差的原因，由卫星、接收机运动引起的距离变化、卫星钟差和接收机钟差等不可能被完全准确地估计，但若对几种方法进行组合，将主要误差项消除，则可用组合后的数据来探测和修复周跳[1]。常见的检测方法主要有载波相位高阶差分法[2]、电离层残差法[3]、多项式拟合法[4]、多普勒积分法[5-6]。对于双频GPS，能使用的数据有伪距、载波相位和多普勒观测值，可采用的方法多为载波伪距组合测量法、多项式拟合法及多普勒法。此外，也可采用自适应滤波的方式实现周跳的探测与修复。而在室内环境下，伪距的测量可靠性极低，故载波伪距组合测量法也不适用于室内伪卫星系统。鉴于此，采用多项式拟合法与多普勒法组合的方式来进行周跳的探测与修复。通过对L1、L2频率的载波相位观测值进行差分，消除电离层延迟及对流层延迟等，采用多项式拟合法处理差分数据，通过多普勒积分法进一步探测是哪个频率发生了周跳及周跳大小。

1 周跳探测的基本原理

1.1 周跳的探测

载波相位观测方程式表示为

Ii(t)+T(t))+Ni+εφ。

(1)

其中：φi(t)为观测频率i为的载波相位观测值；λi为观测频率为i波长；Ii(t)为电离层延迟。

由于观测值受接收机钟差、大气延迟等各种误差的影响，可利用差分的思想，将相邻2个观测频率之间视为2个独立的观测站，从而这2个频率之间可构成超短基线。因此，可基本消除电离层延迟和对流层延迟，在短时间内各种误差的变化量非常小，可视为上述2站的观测时间同步。对L1、L2频段的载波观测值进行差分：

ΔL(t)=λ1φ1(t)-λ2φ2(t)=

(2)

其中Δλ、ΔN分别为组合后的波长和模糊度。

1.2 多项式拟合法探测周跳

多项式拟合法是根据k个载波相位观测值拟合一个n阶多项式，根据多项式估计下一时刻的观测值，并与实测值作比较来探测并修复周跳[4-9]。其数学模型为

φi=a0+a1(ti-t0)+a2(ti-t0)2+…+

an(ti-t0)n,(i=1,2,3,…,k;k>n+1)。

(3)

将k个无周跳的载波相位观测值ΔL代入式(3)，进行多项式拟合。用最小二乘法求得多项式的系数，并利用拟合后的残差Vi计算本次拟合的误差：

(4)

对于双频接收机，直接使用原始观测量进行求解会包含许多非偶然误差。因此，为了消除钟差影响，可采用2个频率间的单差数据。

1.3 多普勒法探测周跳

由于多项式拟合法采用的是频率间单差数据，虽然能探测周跳的发生，但不能确定周跳发生在哪一颗卫星上，因此，需要用多普勒法进一步判断。

GPS多普勒D表示瞬时载波相位变化率，

D=dφ/dt，

(5)

其中：φ为载波相位；t为观测时刻。因此，可通过多普勒积分来探测周跳，

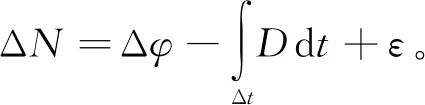
(6)

其中：ΔN为采样时间间隔Δt内的周跳；Δφ为采样时间间隔Δt内的载波相位增量；ε为测量误差。对式(6)采用梯形积分公式即可获得较高的积分精度，有

(7)

其中，Dt、Dt-1为采样时间间隔Δt前后2个时刻的多普勒观测值。当|ΔN|大于某一门限σ时，则认为发生了周跳。

1.4 双频差分周跳探测与修复

双频差分周跳探测与修复方法中，联合使用多项式拟合和多普勒积分法探测周跳的算法流程如图1所示。

1)对接收机接收到的2个频率的载波相位进行差分，得到频率单差值ΔL。

2)根基多项式拟合原理，选取k个无周跳的单差观测数据进行多项式拟合。

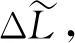
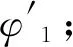
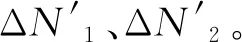
(8)

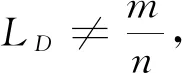
10)进行下一历元的判断，直至程序结束。

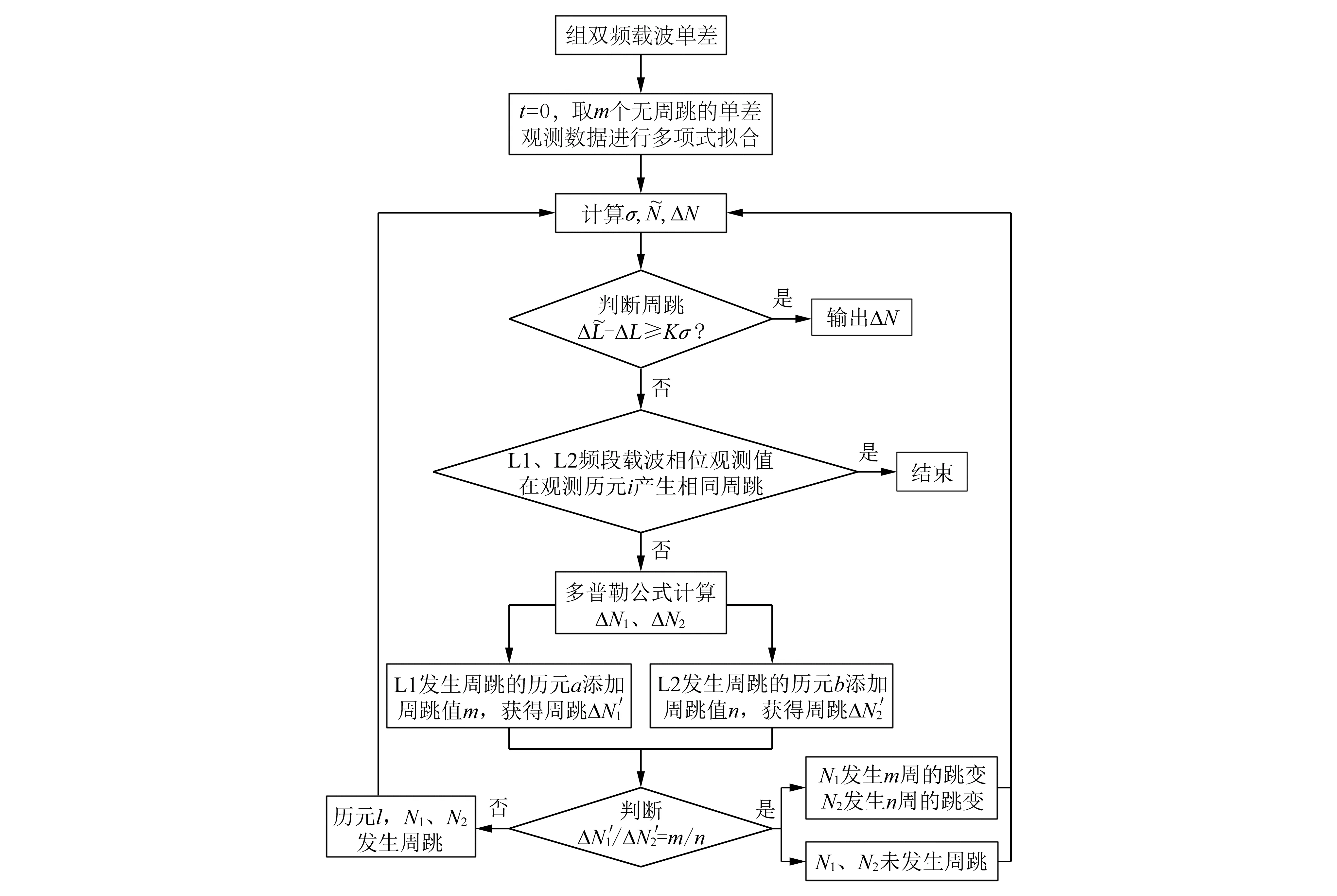
图1 双频差分周跳探测与修复流程图

2 实验与分析

选用2018年4月17日于桂林电子科技大学采集的数据，数据取样间隔为1 s，取L1载波相位观测值和L2载波相位观测值的共300个历元。经反复试验，多项式拟合参数取k=14，n=3,h=5，σmin≥0.1，人为地在L1载波相位观测值的第150、200个历元分别加入2周、3周的周跳；在L2载波相位观测值的第100、150、200个历元分别加入2周的周跳，并令m=3，n=2。

图2为采样率为1 s的多项式拟合探测周跳的结果。从图2(a)可看出，在第100历元处约有2周的跳变，第200历元处约有1周的跳变，可看出外推值和实测值有明显差异，因此,可判断出这几个历元发生了周跳。继续执行步骤6)，在L1、L2频段信号所有载波相位上分别添加m、n周的周跳后，得到多普勒探测周跳的结果。

图2 采样率为1 s的多项式拟合探测周跳的结果

图3为采用多普勒法区分周跳发生在哪个频率上的周跳。从图3可看出，对于L1频率，第100历元处约有3周的跳变，第150历元处约有5周的跳变，第200历元处约有6周的跳变；对于L2频率，第100、150和200历元处分别有4周的跳变。由此可以判断出2个频率在第100、150和200历元处发生了周跳。

图3 1 s采样率多普勒法探测结果

根据双频差分周跳探测的判断条件，如表1所示。图2中第100和200历元处有周跳，150历元处无周跳，但图3中150历元处有周跳，可知在该历元2个频率的周跳相同，且m=3，n=2，因此2个频率的周跳值均约为2周。同时可判断出第100、200历元处周跳值并未包含3/2的倍数，因此L1载波相位观测值的第100、200个历元分别约为0周、3周的周跳，L2载波相位观测值的第100、200个历元分别约为2周。

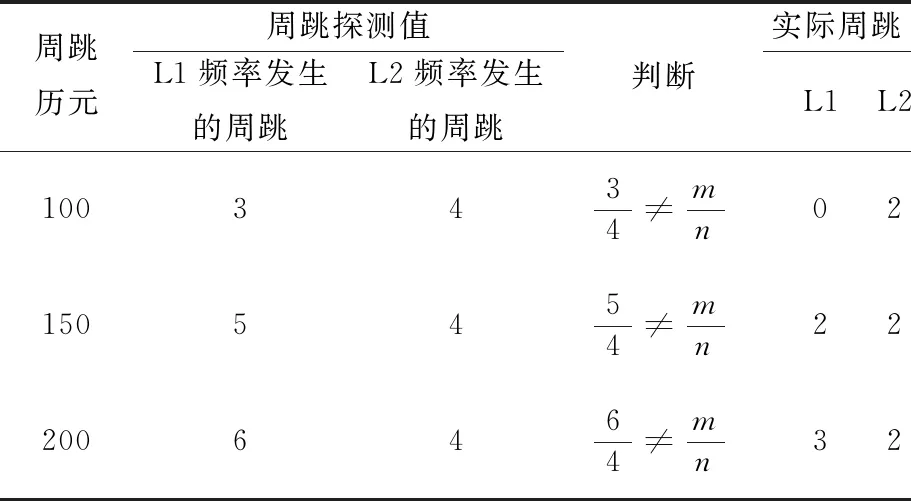
表1 双频差分周跳探测

3 结束语

采用多项式拟合法和多普勒法组合的方式进行双频差分周跳的探测与修复，能够准确探测和修复1周以上的周跳。本算法的数学模型简单易实现，有效的提高了周跳的探测精度，是一种较为有效且实用的单频周跳探测和修复方法。目前，本算法是基于GPS静态定位数据得出的，对于动态实时数据的适用性需要进一步验证，这将在后续工作中重点研究。