类电磁粒子滤波预估耙吸挖泥船土壤粒径研究

俞孟蕻,蔡 磊,苏 贞,柏祥华

(1. 江苏科技大学 电子信息学院, 镇江 212100)(2. 海洋装备部驻南京地区第一军事代表室， 南京 210006)

在耙吸挖泥船进行疏浚作业的过程中,土壤粒径与疏浚作业其他参数有着密切的关系,如静水沉降速度、沉积物实际密度等,土壤粒径的平均值对于泥水的沉降过程有着很重要的影响[1]．文献[2]用标准粒子滤波估计土壤粒径,证明粒子滤波对于此方面的可用性．文献[3]使用模式搜索法对土壤参数进行估计．文献[4]使用粒子滤波对溢流密度,溢流流量进行估计．文献[5]证明粒子滤波对于土壤粒径与沙床高度的估计优于模式搜索法[5]．虽然标准粒子滤波算法能较好地对土壤粒径进行估计,但存在一些缺陷,如粒子的退化问题与样本贫乏问题,导致土壤粒径估计不够精确[6]．

文中在耙吸挖泥船动态沉积模型的基础上,基于类电磁机制粒子滤波(electromagnetism-like mechanism particle filter,EM-PF)估计土壤粒径,通过将采样粒子视作带电粒子,模拟带电粒子之间吸引与排斥机制,使采样粒子朝着更优的解值移动,又因为排斥力的作用,使粒子保持一定的间距,从而缓解粒子滤波算法的粒子退化与样本贫乏问题[7]．相对于标准粒子滤波(basic particle filter,BPF)，类电磁机制粒子滤波能更精确地对土壤粒径进行估计．

1 土壤粒径估计

关于土壤粒径的随机游走数学模型[8]:

ddm(t)=0dt+dwdw(t)

(1)

式中:dm为土壤粒径;d为变化的数值;wdw(t)是拥有恒定的标准差的维纳过程．

耙吸挖泥船的沉积模型为：

(2)

式中：mt、vt分别为装舱质量、装舱体积；ms为沙床质量；Qs为泥沙沉积流量；ps为泥沙沉积密度,泥沙沉降流量与溢流密度可以由一维沉降模型[9-10]与水层模型[11]得到；Qi、pi分别为进舱流量与进舱密度；Qo、po分别为溢流流量与溢流密度．

沉积过程如图1．

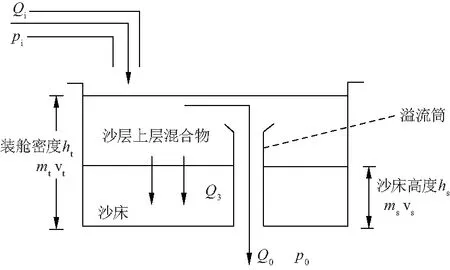
图1 耙吸式挖泥船沉积模型Fig.1 Sediment model of rake suction dredger

在耙吸挖泥船沉积模型的基础上,建立对于粒径的估计模型,其状态方程X、观测方程Z为[5]:

(3)

(4)

式中:ht为装舱高度;mt为装舱质量；vt为装舱体积；hs、vs和ms分别为沙床高度与沙床体积;S为挖泥船舱容的面积；dm为土壤粒径;w和v为系统噪声和观测噪声;Ts为采样周期．

2 基于类电磁机制的粒子滤波

将类电磁机制代入到粒子滤波算法当中,用来进行土壤粒径的估计,使粒子滤波样本贫乏与粒子退化现象得以减轻．

类电磁机制粒子滤波算法受力原理(图2)说明,通过合力的作用,将粒子带到目标函数值更高的位置[12]．如图2,将采样的粒子视作带电粒子,这3个粒子中,3号粒子目标函数值最大,是当前的最优粒子,2号次之,1号目标函数值最小．由下文公式(5)可知,3号吸引1、2号粒子;2号排斥3号,吸引1号;1号排斥2号与3号．2号和3号朝着3号粒子所代表的最优粒子的方向移动,最小的1号朝着2号移动,因为2号是目标函数值次优粒子,所以1号也是朝着目标函数值更高的方向移动．这样粒子就移动到了目标函数值,即权值更大的位置,后验概率密度增加,预测的结果更加精确，从而缓解了粒子退化问题,提高了精确度,优化了粒子滤波的效果，同时,排斥力也保证了粒子的多样性,缓解了粒子贫乏问题．

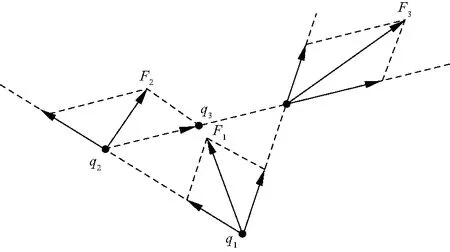
图2 类电磁机制粒子滤波粒子受力图Fig.2 Particle force diagram of electromagnetic-like mechanism particle filter

将改进的类电磁机制带入粒子滤波的具体步骤如下:

第一步 初始化相关参数，然后进行采样,从而产生一个包含M个粒子的粒子集，设置迭代的次数与移动系数等参数．

第二步 对状态值与观测值通过状态方程与观测方程进行一步预测．

第三步 计算权值．

第四步 将类电磁机制算法带入粒子滤波[7]．

将每一个采样的粒子视为一个带电粒子．首先通过循环找出权值最大的粒子，并将权值最大的粒子记作Xbest．将f(xi)记作第i个粒子的权值，将Xbest的权值记为f(xbest)，n为状态变量的维数．通过公式

(5)

计算每个粒子进行带电粒子的电荷量q[13],再计算粒子受到的合力Fi[14]:

(6)

根据公式(6)计算带电粒子所受到的合力．在计算出每个粒子受到的合力之后,根据公式(7)计算带电粒子受到合力的作用从而朝受力方向移动的距离[15],更新后的粒子Xi为:

Xi=Xi+v*Fi*Y/‖Fi‖

(7)

式中：v为移动系数；Y为在(0,1)上均匀分布的随机数．

当带电粒子移动完成之后,更新了位置．接着重新计算权值,计算完成之后进行归一化．

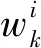
第五步 重采样,根据粒子权值大小进行重采样,复制权值大的粒子,淘汰权值小的粒子[16]．完成类电磁机制的粒子滤波算法用于土壤粒径估计．状态的估计值[17]为:

(8)

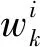
首先，执法主体混乱，执法尺度不一，分工不明确。在我国，查处商业贿赂犯罪的执法部门主要有法院、检察院、工商部门以及公安机关。但是正是这些看似庞大的反商业贿赂执法队伍往往由于职能分工上的不明确不仅会出现政出多门、多头执法的混乱后果，还会导致不同部门在对查处商业贿赂的标准上执法尺度不一，在一定程度上加大了执法的成本。

3 土壤粒径的应用与仿真对比分析

使用EM-PF对土壤粒径进行估计,并与BPF进行对比,检测EM-PF对土壤粒径的估计是否能起到想要的正面效果．

设置装舱参数与粒子滤波参数,模拟装舱参数见表1．

表1 模拟装舱参数Table 1 Simulated loading parameters

粒子滤波参数系统噪声与观测噪声的标准差见表2．

表2 粒子滤波系统噪声与观测噪声的标准差Table 2 Standard deviations of noise and observation noise of particle filter system

对于初始的参数设定,设定采样时间为1 s,总时间为1 200 s,设粒子总数为100,门限值为50．设定水的密度,石英的密度为固定值．设定移动系数为1．对同一土壤的工作状态下进行土壤的粒径估计，并且在程序中设置均方根误差(root mean squard error, RMSE)的计算[18]．

(9)

3.1 土壤粒径保持不变情况下(静态)预测对比

由图3中可以看出,在同一土壤的工作环境下,使用EM-PF估计土壤粒径比BPF更接近于真实值．表3说明了类电磁机制粒子滤波EM-PF对土壤粒径预估拥有更好的精确度,对于同一土壤情况下的粒径估计有更好的估计能力．

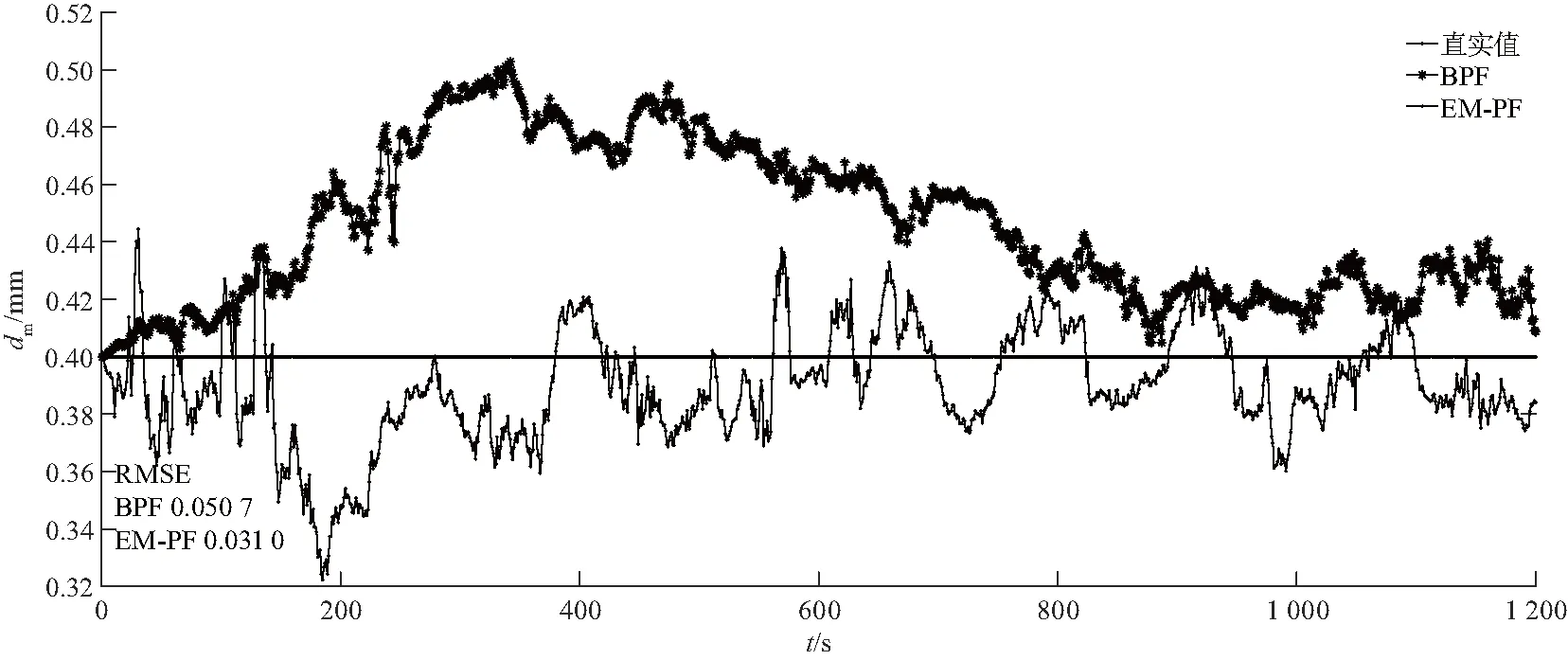
图3 土壤粒径保持不变情况下(静态)的BPF与EM-PF预测对比Fig.3 Comparison of BPF and EM-PF prediction under the condition that soil particle size remains unchanged (static)

表3 土壤粒径保持不变情况下两种粒子滤波方法的平均RMSETable 3 Average RMSE of the two particle filtering methods when the soil particle size remains unchanged

3.2 土壤粒径发生突变情况下(动态)预测对比

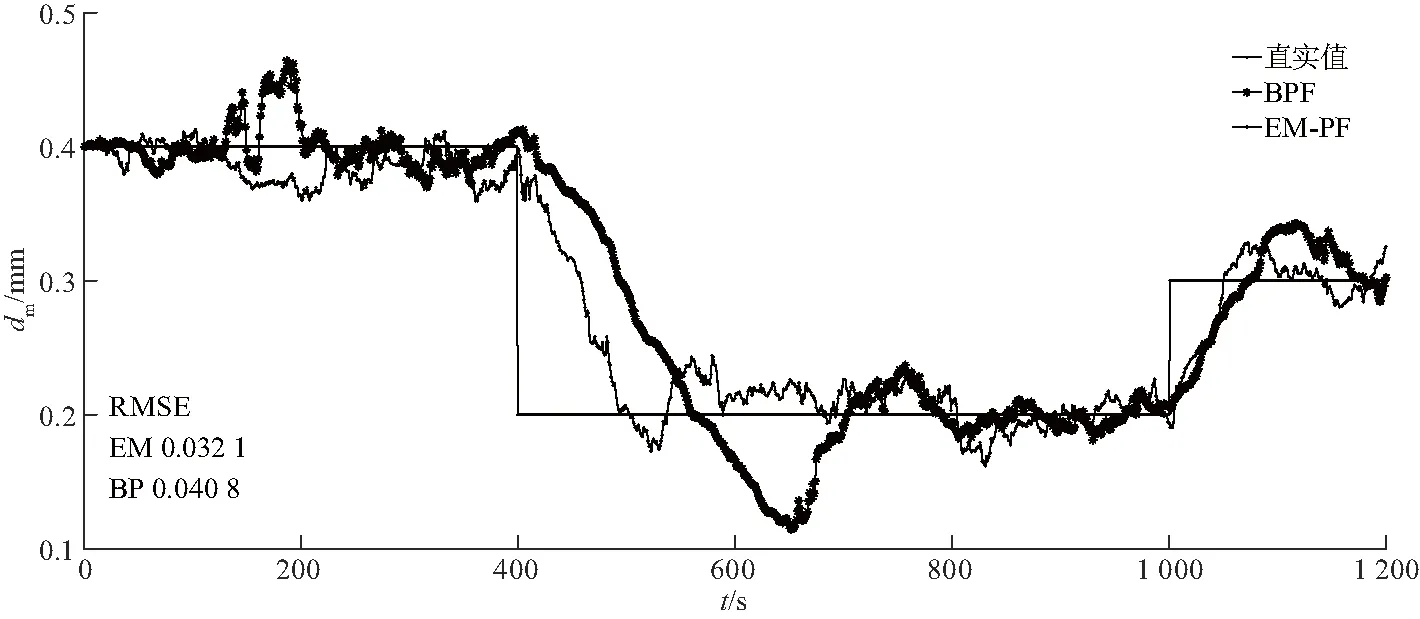
图4 土壤粒径发生突变情况下(动态)的BPF与EM-PF预测对比Fig.4 Comparison of BPF and EM-PF prediction under abrupt change of soil particle size (dynamic)

表4显示,EM-PF均方根误差RMSE也相对较小,说明在土壤工况发生突变时(动态),EM-PF有着更精确的估计能力,对于土壤粒径的估计有优化作用．

表4 土壤粒径发生突变情况下两种粒子滤波方法的平均RMSETable 4 Average RMSE of the two particle filtering methods in the case of soil particle size mutation

3.3 土壤粒径发生突变情况下5组预测对比

为防止仅一次实验对比带来的偶然性,对BPF、EM-PF重复试验5组,进行预测对比,见图5、6;每次的均方根误差RMSE见表5．继续把次数扩大至30次,结果如表6．由图5、6及表5、6可以看出,当土壤粒径真实值发生突变时,类电磁机制粒子滤波EM-PF比标准粒子滤波BPF在估计土壤粒径上更加精确,追踪速度更快．

图5 土壤粒径发生突变情况下BPF 5组预测Fig.5 Prediction of 5 groups of BPF in the case of soil particle size mutation

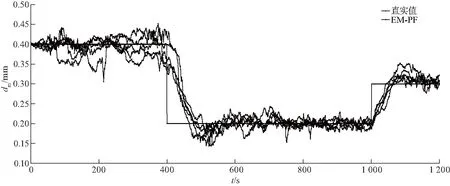
图6 土壤粒径发生突变情况下EM-PF 5组预测Fig.6 Prediction of EM-PF group 5 in the case of soil particle size mutation

表5 土壤粒径发生突变情况下5组数据的平均RMSETable 5 Average RMSE of 5 groups of data in the case of soil particle size mutation

表6 土壤粒径发生突变情况下30组数据的平均RMSETable 6 Average RMSE of 30 groups of data in the case of soil particle size mutation

3.4 采样时间对均方根误差RMSE的影响

由表7,随着采样时间的增大,其精度也随之而减小,EM-PF均方根误差RMSE增加较少．

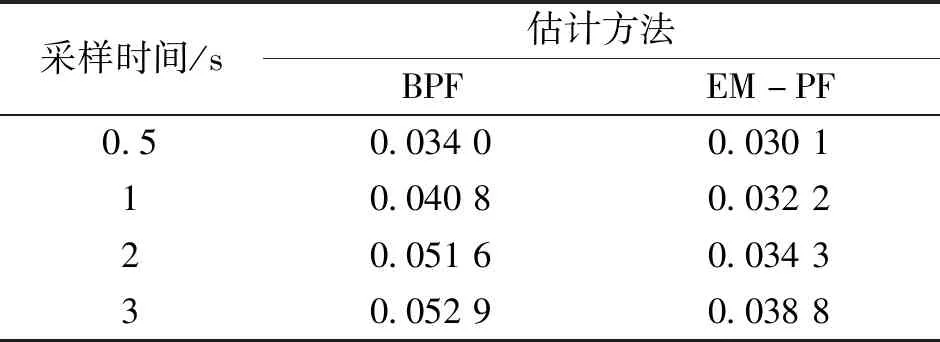
表7 采样时间对RMSE的影响Table 7 Impact of sampling time on RMSE

3.5 系统噪声信号wdm对均方根误差的影响

在保持采样时间为1 s的情况下,其他参数也不变,只变化系统噪声wdm,比较两者RMSE，见表8．由表8可知,随着噪声wdm的增大,两种算法的均方根误差也随之而增大．

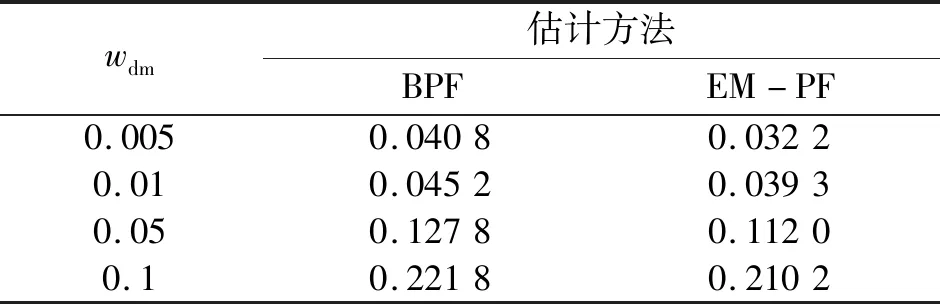
表8 系统噪声wdm对RMSE的影响Table 8 Influence of system noise wdm on RMSE

3.6 更多突变情况下的预测对比

图4显示发生了两次突变,图7增加到4次突变,可以更明显地看出复杂工况下EM-PF的动态追踪能力的优势．图7与表9,复杂多变的情况下,EM-PF动态追踪能力相对优势越明显．

图7 突变4次情况下的BPF与EM-PF预测对比Fig.7 Comparison of BPF and EM-PF prediction under 4 mutations

表9 土壤粒径发生突变4次情况下BPF与EM-PF的平均RMSE对比Table 9 Comparison of the average RMSE of BPF and EM-PF in the case of soil particle size mutation for 4 times

3.7 类电磁机制粒子滤波与粒子群粒子滤波针对复杂突变情况的对比

将类电磁机制粒子滤波与粒子群粒子滤波(particle swarm optimization particle filter，PSO-PF)进行对比,从图8和表10、11可以看出,对于估计粒径,类电磁机制粒子滤波相比于粒子群粒子滤波的动态追踪能力更强,精确度更高．

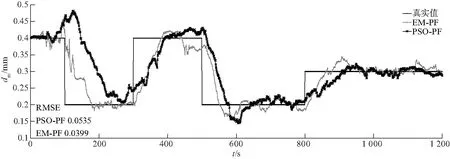
图8 突变4次情况下PSO-PF与EM-PF预测对比Fig.8 Comparison of PSO-PF and EM-PF prediction under 4 mutations

表10 土壤粒径发生突变4次情况下PSO-PF与EM-PF的平均RMSE对比Table 10 Comparison of the average RMSE of BPF and EM-PF in the case of soil particle size mutation for 4 times

表11 土壤粒径发生突变情况下30组数据的平均RMSETable 11 Average RMSE of 30 groups of data in the case of soil particle size mutation

3.8 类电磁机制粒子滤波实船数据估计

图9、10分别针对长江口与黄骅港的工况下,采用EM-PF对实船土壤粒径的估计结果．

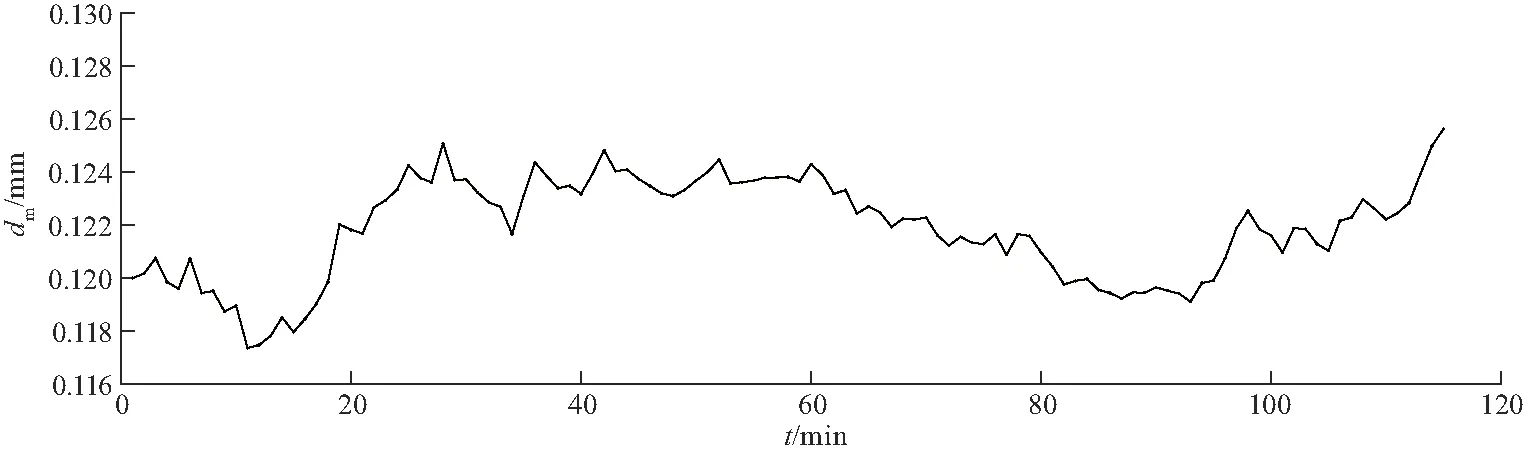
图9 EM-PF对长江口土壤粒径估计Fig.9 EM-PF estimation of soil particle size in the Yangtze river estuary

从图9、图10可知,长江口土壤粒径变化较大,长江口本身土壤为0.05～0.20 mm的细粉砂,黄骅港土壤粒径变化则较为平缓,黄骅港为淤泥粉砂质．EM-PF方法对土壤粒径估计结果与实际结果是相符的．

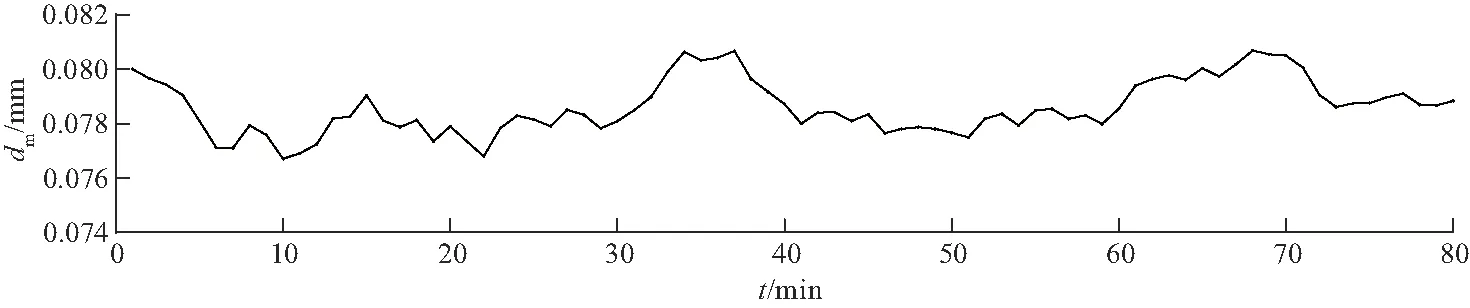
图10 EM-PF对黄骅港土壤粒径估计Fig.10 EM-PF estimation of soil particle size in huanghua port

4 结论

(1) 基于静态与动态土壤粒径的综合考虑,使用基于类电磁机制粒子滤波EM-PF估计粒径的效果要优于使用标准粒子滤波BPF的效果．

(2) 多次重复实验的数据与均值证明,类电磁机制粒子滤波EM-PF估计粒径的效果要优于标准粒子滤波BPF、粒子群粒子滤波PSO-PF,预防单次实验造成的偶然性．

(3) 当土壤粒径真实值发生突变时,类电磁机制粒子滤波EM-PF比标准粒子滤波BPF和粒子群粒子滤波PSO-PF,在估计土壤粒径上更加精确,追踪速度更快．

(4) 随着采样时间的增大,两种算法精度也随之而减小,EM-PF均方根误差RMSE增加较少;随着噪声的增大,两种算法的均方根误差也随之而增大．

(5) 将实船数据带入后,类电磁机制粒子滤波EM-PF对土壤粒径的估计符合实际的结果．