基于融合视觉增强的水下机器人-机械手系统抗扰控制研究

陈 伟,张宇航,张浩哲,王 磊,王伟然,李 旭

(江苏科技大学 电子信息学院,镇江 212100)

水下机器人-机械手系统(underwater robot-manipulator system，UVMS)依靠视觉系统和机械手,在极端危险的大深度领域完成人工无法胜任的工作,广泛应用于堤坝检测、水产养殖、水下清污、海洋管线检修等领域[1]．然而在真实海洋环境中,UVMS面临水下光学感知弱化、外部复杂海洋环境不确定性扰动等问题，因此，目前实现抗干扰水下自主作业仍有难度．

水体对光易引起散射与吸收,造成图像对比度低、光学畸变等诸多不利因素,降低UVMS自主水下目标精细识别能力．在多种水下图像增强方法中,基于颜色恒常理论的水下图像增强方法脱颖而出,例如Retinex算法[2]、基于Retinex算法的非线性图像增强算法[3]、多子块协同单尺度Retinex算法[4]等都得到了方案论证．Retinex算法具有颜色恒常效果,在保留色彩信息基础上,提高人工光源图像暗区域内的细节部分,达到图像局部对比度显著提高的效果．为解决Retinex产生的“光晕”现象，引入双边滤波方法，是一种带有边缘保护的图像降噪平滑滤波器,能有效消除光照不均对图像的影响[5]．融合双边滤波的Retinex算法在车辆故障检测系统[6]、无人机侦察[7]、矿井勘探[8]等行业得到应用．而在自然光源主导的浅水区域或人工光源加持的深水区域,采用融合双边滤波的Retinex优化算法研究水下图像增强是具有一定挑战性的．

真实水下环境的复杂性和不可预测性提高了UVMS精准控制的难度．国内外学者提出多种控制策略,例如基于模拟负载的PID控制[9]、自适应非奇异积分终端滑模控制[10]、自适应抗扰控制方法[11]、冗余度分解方法[12]等都在UVMS机械手控制中得到了实验验证,但大多局限于没有扰动或部分扰动.为解决建模不精确问题,提出许多方法,如基于干扰观测器的模糊自适应S面控制[13]、基于滑模观测器的模型预测控制[14]、基于扩展卡尔曼滤波器(extended Kalman filter，EKF)的鲁棒快速管模型预测控制[15]．其中EKF作为系统状态观测器,可以对未知海流参数的水下机械手运动进行显性估计和补偿,结合反馈线性化控制还可以应用于机器人本体的动态定位,从而提高UVMS工作稳定精度,实现更复杂的水下作业．

基于融合视觉增强的UVMS抗扰控制方法如图1．采用融合图像增强算法可提高UVMS观测性能,并为水下机械手实现伺服控制提供准确的目标信息．将EKF和线性反馈转换控制方法结合利于应对作业过程中出现的不确定性扰动,提高水下作业机动性能,提升UVMS水下视觉伺服控制能力．

图1 基于融合视觉增强的UVMS抗扰控制方法Fig.1 UVMS anti-interference control method based on fusion vision enhancement

1 集总不确定性扰动下UVMS精确建模

UVMS运动主要涉及3个坐标系:大地坐标系、本体坐标系和机械手坐标系,如图2．

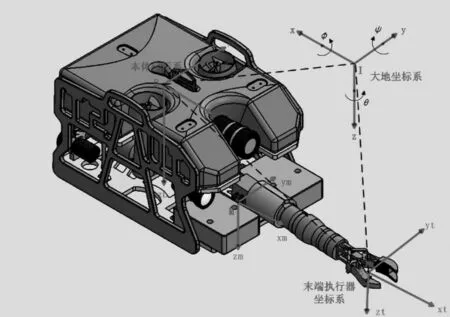
图2 水下机器人-机械手系统的坐标Fig.2 Coordinates of the underwater vehicle- manipulator system

设定I(x,y,z)为大地坐标系(配置空间),B(xb,yb,zb)为水下机器人本体坐标系,E(xt,yt,zt)为机械手坐标系(任务空间)．利用牛顿-欧拉和递推牛顿-欧拉公式建立配置空间的机械手动力学方程:

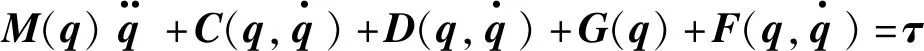
(1)

(2)

(3)

(4)

(5)

(6)

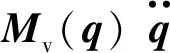
任务空间和配置空间的转换关系为:

μ=f(q)

(7)

式中：μ=[xtytzt]T为任务空间向量；f(q)为正向运动学向量．对上式求导:

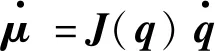
(8)

式中：J(q)为雅可比矩阵,构成配置空间与任务空间的速度映射关系．

将式(1)转换为任务空间下机械手动力学方程:

(9)

式中：Mμ、Cμ、Dμ、Gμ、Fμ分别为任务空间中机械手惯性矩阵、科氏力矢量和向心力矩阵、阻尼矩阵、恢复效应矢量、动态耦合矢量；τin为控制输入向量．

UVMS水下作业时机械手面临的各类扰动主要分为:系统不确定性扰动、外界波浪流扰动、非结构化随机扰动[16-18],因此其运动方程是高度非线性的,将上述不确定性扰动归结为集总不确定性扰动τdis,最后得任务空间的水下机械手动力学方程:

(10)

2 水下融合视觉增强算法

2.1 融合增强过程

文中提出基于双边滤波和MSR优化算法的融合图像增强方法．如图3,对初始图像进行双边滤波,得到粗略图像和细节图像;将粗略图像进行MSR优化算法,实现颜色校正和细节还原;将增强后的粗略图像与细节图像融合,最终得到输出图像．其中,MSR优化算法加入了动态图像信息补偿步骤,使MSR算法不再局限于单一环境,扩宽了该算法的运用范围．

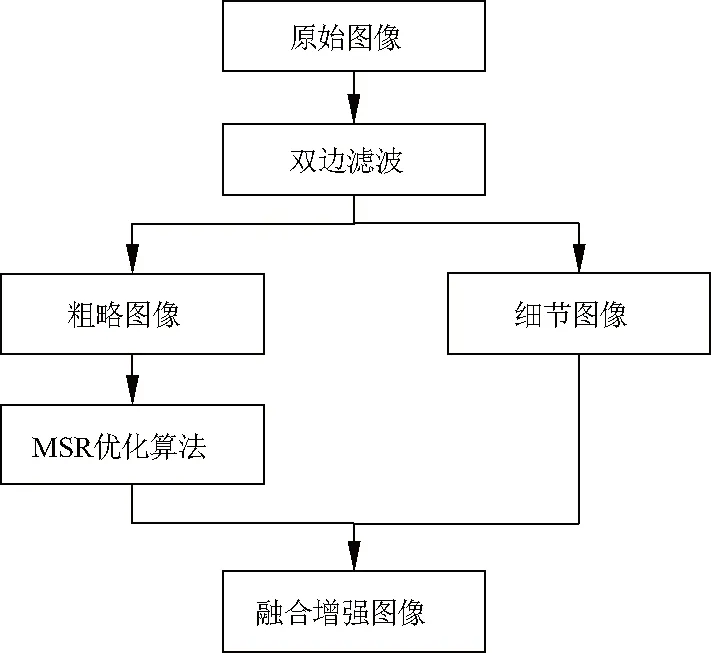
图3 融合图像增强算法Fig.3 Fusion image enhancement algorithm

2.2 基于MSR优化算法的视觉融合增强

MSR优化算法流程如图4．首先,对输入图像进行预校正,减少主导颜色;其次,利用强度通道执行改进MSR算法,估计得到反射率和照明分量;之后,恢复图像,补偿动态;最后,差别性的保留原始图像的颜色．

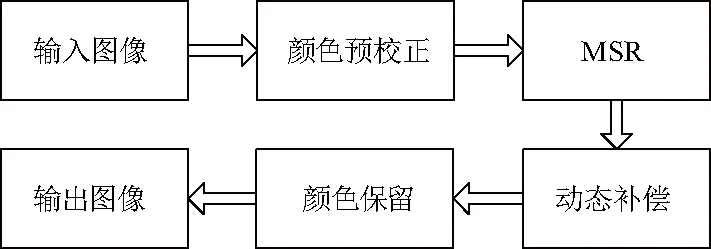
图4 MSR优化算法Fig.4 MSR optimization algorithm

2.2.1 颜色预校正

根据光学原理,水体吸收作用是在可见光的波长范围内,光的波长越长,水对光的吸收能力越强,故水下图像总是被绿色或蓝色主导[19]．因此,水下图像颜色预校正是必不可少的一步．

引入Imean和Ivar作为输入图像的平均值和偏差值,每个通道的最大值Imax和最小值Imin可以通过以下方式获取:

I(i)max=I(i)mean+λμI(i)var
I(i)min=I(i)mean-λμI(i)var

(11)

式中：i∈{R G B}；μ为动力学标称；λ为颜色均衡标度．

颜色预校正后的图像表示为:

(12)

2.2.2 带强度通道的MSR算法

人观察到的物体颜色是由物体本身的属性有关,即主要由物体表面反射能力决定[20]．观察到的图像表示如下:

S(x,y)=L(x,y)×R(x,y)

(13)

式中：R(x,y)为反射光图像,决定了该图像具有的内在性质;L(x,y)为照度图像,可以通过中心/环绕函数估计得到;S(x,y)为观察者所获得的图像．通过上式可以反推得原始反射光图像表达式,并对等式两边同时取对数:

logR(x,y)=logS(x,y)-logL(x,y)

(14)

引入高斯环绕函数构建单尺度Retinex,但其不能同时提供动态范围压缩和颜色恢复,而MSR算法通过权值叠加弥补了上述缺点,定义式如下:

log(F(x,y,σn)×S(i)(x,y)))

(15)

式中：N为标度数；ωn为每个标度的权值；log(S(i)(x,y))-log(F(x,y,σn)×S(i)(x,y))为单尺度Retinex的输出图像,×为卷积运算,F(x,y,σn)为各标度的高斯环绕函数；i∈{R G Bρ},ρ为强度通道,用于保存图像颜色．

(16)

式中：m为图像通道数量．

2.2.3 动态补偿

如式(14),MSR算法通过线性变换从对数域中获得增强图像．在恢复过程中往往要考虑增益和偏差，这两个特征量往往需要针对指定图像进行调整,无法适用于所有水下图像增强,会大大减弱该算法的效果,降低实用性．

文献[21]在CIE-Lab颜色模型中运用了自适应拉伸方法,建立亮度参数归一化的拉伸公式,最终得到高对比度、平衡化、饱和化的清晰图像．在此基础上,文中将动态适应拉伸方法用于图像信息补偿,建立如下补偿公式:

I(i)MSRMAX=I(i)MSRMEAN+μI(i)MSRVAR
I(i)MSRMIN=I(i)MSRMEAN-μI(i)MSRVAR

(17)

式中：I(i)MSRMAX和I(i)MSRMIN分别为MSR处理后每个通道的最大值和最小值；I(i)MSRMEAN和I(i)MSRVAR分别为MSR输出图像的平均值和偏差值；μ为动态范围；i∈{R G B}．

动态补偿后的MSR图像:

(18)

2.2.4 颜色保留

MSR算法容易将颜色信息丢失,造成颜色饱和度降低的情况，采用具有颜色修复的MSR算法(MSRCR)解决了上述问题,但面临着颜色增益和偏差的问题,局限了其使用效果．将原始图像色度信息进行一定比例放大,从而避免后续过多的颜色增益和偏差,生成更接近于原始颜色的图像．

(19)

式中,i∈{RGB}；α为颜色保留系数,I(i)mean为原始图像的平均值；I(S)DCMSRMEAN为MSR算法动态补偿后的强度通道平均值；I(i)DCMSR为MSR算法动态补偿后的图像；I(i)DCMSRCP为MSR优化算法生成的最终图像．

3 机械手抗扰控制器

在UVMS具备精细感知能力的基础上,设计优良的机械手抗扰控制器,使系统出现内外不确定性扰动时能做出实时调整,实现高精度水下视觉伺服抓取任务．通过扩展卡尔曼滤波器(EKF)和空间反馈线性转换,取代传统干扰控制器,补偿内外干扰下机械臂的位移,维持机械手系统稳定．

UVMS作为非线性环境下的冗余系统,内外扰动瞬息万变．对输出系统的所有状态参数进行反馈控制,降低了效率和实用性．如果在可控误差范围内,选取定量参数估计未知状态,往往变得易于实现且高效．因此,通过EKF和转换矩阵来估计模拟出系统位置和速度,补偿实时偏差,以达到机械手系统水下稳定作业的目的．机械手抗扰控制系统为:

(20)

(21)

(22)

式中：s为系统状态向量,τin为控制输入向量,τdis为控制过程中的集总不确定性扰动量．

系统状态检测过程分为预测和校正阶段，预测过程为:

(23)

(24)

运用上节建立的UVMS本体运动学方程,对其进行预测状态后的校正环节:

Kn=PnGnT(GnPnGnT+Fn)-1

(25)

(26)

(27)

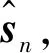
(28)

式中：k1和k2为待设计和调节的常系数矩阵；α和β为水下机械手的自由度指数系数分量．

依据文中建立的UVMS动力学方程,便可由抗扰控制器估计出状态偏差量,经空间转换矩阵,换算为UVMS本体系统的状态补偿量,从而实现本体水下动态定位,配合机械手完成更复杂的水下作业．

4 实验研究

利用研制的UVMS分别进行水下视觉增强实验和机械手视觉伺服抓取实验,该水下机器人-机械手系统搭载三自由度电动机械手和网络摄像机,装备两个垂直电力推进器、两个纵向电力推进器和可加装的侧向推进器,具备纵荡、垂荡、横荡、横摇、艏摇、纵摇的六自由度运动,选用吸水率<1%(24 h)的固体复合泡沫,可以承受2 000～36 000英尺的水下环境,浮心高、重心低的开架式结构优化了纵向和横向正稳性,在俯仰和摇摆轴上实现进一步稳定．内置惯导、测深、电导温深(CTD)等环境感知系统,预留了超短基线接口，系统如图5．

图5 水下机器人-机械手系统Fig.5 Underwater vehicle-manipulator system

4.1 水下视觉增强实验

对水下图像进行了融合图像增强算法,同时与MSR算法和双边滤波算法进行成像效果对比和数据分析．图6成像效果表明,MSR算法补偿了水池底部尘埃的细节信息,在增强水下图像色彩的同时很好的保持了颜色恒常性,但出现了边缘锐化不足、纹理不清晰等缺点,这点在物体A上显得尤为明显．双边滤波算法考虑了卷积核中像素与中心像素之间相似程度的影响,在保留了边缘的同时消除了噪声,增强了图像的层次感,这在物体B的成像效果中得到证明,但增强后的图像明显颜色偏淡、色彩失真,背景细节丢失严重．相比之下,融合增强算法补偿了两者的成像缺点,物体A、B的纹理清晰,背景细节得到还原,能够更好的还原海参模型形状和实验环境细节,颜色也较双边滤波得到了收敛,整体画面自然,更贴近实际水下环境．同时,图像细节量的增多为后续水下目标识别与测距提供了丰富的参考数据,解决了识别过程带来对象不明的问题．

图6 水中目标物视觉增强对比Fig.6 Comparison of visual enhancement of underwater targets

表1数据对比表明,融合增强算法在亮度、对比度、清晰度上得到了很大的提升,同时控制亮度,使其保持在合理裕度内,避免双边滤波处理后类似于曝光现象的缺点．信息熵的提高证实了融合算法在细节处理方面的有效性．

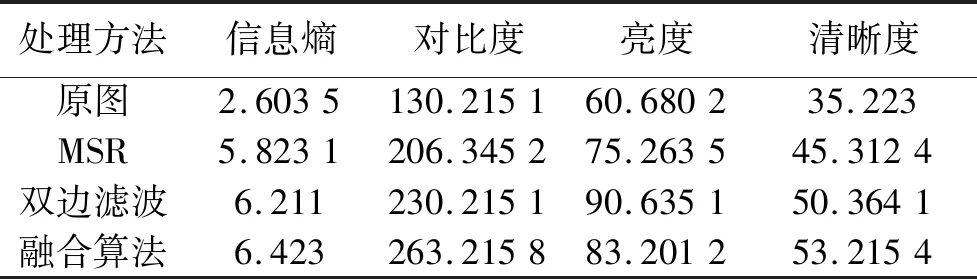
表1 图6各种算法结果分析Table 1 Analysis of the results of various algorithms in figure 6

4.2 水下机器人-机械手系统抗扰抓取实验

视觉伺服抗扰抓取实验概述如下:融合惯导、测深等传感器检测系统在扰动下的姿态,运用扩展卡尔曼滤波器(EKF)和空间反馈线性转换矩阵将本体位移量转化为机械手关节矢量,利用多关节机械手的扇形工作范围特点,补偿UVMS本体未及时修正或过补偿的位移量．该矢量数据将结合视觉解算后的数据得到最终的关节电机反馈角度．

研究对象是三自由度控制能力的UVMS,该模型参数如表2,控制器的参数选择为:

表2 UVMS模型参数Table 2 UVMS model parameters

α=1.2I3，β=0.5I3k1=[2 0.5 0.5]T,

k2=[0.5 1 0.5]T,g=0．

在5～15 s范围内模拟1～3节混合水流干扰:

t=0～5 s:T=0.

(29)

生成UVMS水下作业过程的机械手末端执行器三维轨迹(图7)，可以看出:机械手在干扰时间段过渡平滑,未出现剧烈波动,伺服控制性能优良,精确快速地对水下目标进行了定点跟踪．

图7 机械手三维轨迹图Fig.7 3D track diagram of the manipulator

如图7(b)中,突现扰动带来机械手y轴方向位移,得益于抗扰控制器,补偿了扰动带来的大范围位移,且在较短的时候内进行系统自调整,证实了基于EKF和空间线性转换的抗扰控制器在水流干扰下对UVMS起到了优良的平衡控制作用,改善了UVMS水下控制性能．

区别于水下工业任务,水下捕捞作业多数工作于海底．对水下捕捞作业影响极大的是由海流产生的介于全水流层(浅水区)与零水流层(海底)中间的湍流边界层．为实现水流湍流层效果,以UVMS作业点为中心的30 m2内,于水面临界点设置横向、纵向2个250 W增氧浪涌水炮,以此模拟全水流层．参照蒲福氏风级对应表,制造和风、四级风下的水流扰动,参考流速5 m/s．

以悬停的UVMS质心为参考原点,经视觉测距获得抓取目标在任务空间的三维空间点(单位:m)为(0.523,0.558,-0.982),逆解出的肩、肘关节转动角度θ1，θ2分别为26.33°和31.22°．机械手运动过程中的相关数据由每个关节中的水下编码器、行程开关等反馈硬件实时记录．图8为抓取海参模型实验过程,图9为关节实时反馈数据．数据表明水下机械手的肩关节最终位置为26.50°,肘关节最终位置为29.10°．

图8 水下抓取实验过程Fig.8 Underwater grab experiment process

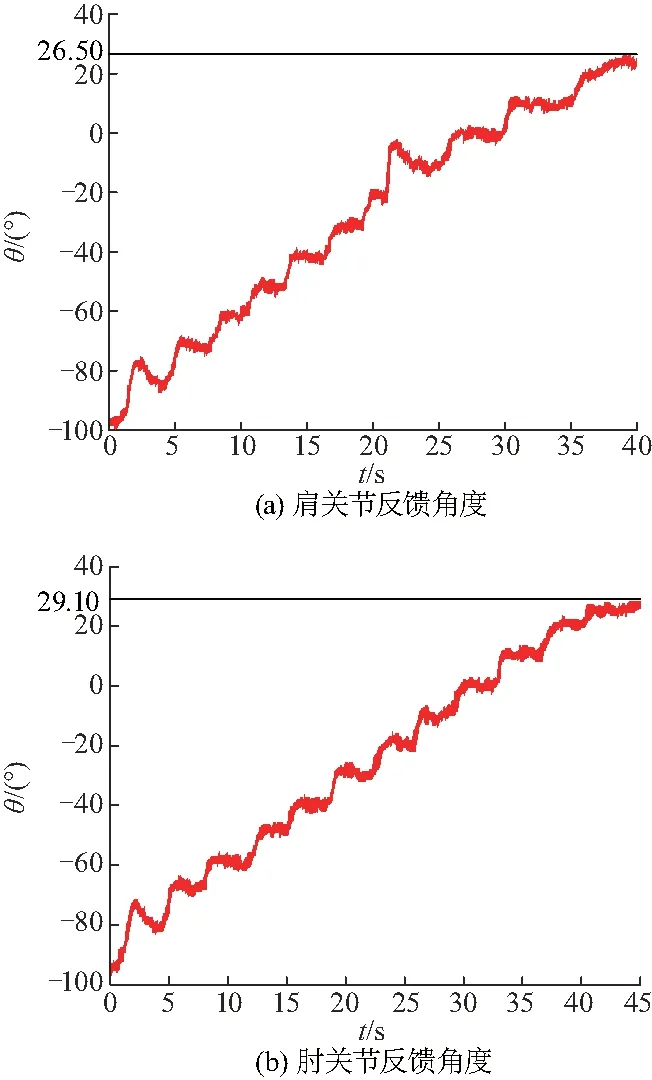
图9 肩关节、肘关节实时反馈角度Fig.9 Real-time feedback angle of shoulder joint and elbow joint

实验分析,水流扰动下的机械手会出现停车不到位和肩关节转角偏大的情况,但转角误差保持在±2°范围,相比于未经图像处理时,成功率提升20%,达到预期控制效果．第一抓取视角如图10,机械手到达实验目标位置,完成指定任务．

图10 伺服控制抓取过程Fig.10 Servo control capture process

5 结论

针对UVMS水下图像成像质量差、抗干扰能力弱的缺点，采用融合图像增强算法,提高了水下图像捕获和分析能力;同时构建集不确定性下UVMS数学模型,为抗扰控制器的设计提供了基础,以获得更好的UVMS抗扰参数．为验证图像增强效果和基于EKF和空间线性转换的抗扰控制器性能,进行水下海参模型抓取实验,测得水下机械臂各关节伺服反馈实时角度和机械手三维轨迹．分析数据表明,机械手精确跟踪目标轨迹的同时保持了UVMS稳定性,实现了在不确定性扰动下UVMS水下作业的任务,验证了图像融合算法在水下成像和细节捕捉方面的有效性．

未来将进一步发展深海中人工光源下的融合增强算法及机械手抗扰控制器状态预测精准度,展开洋流扰动下UVMS实际海底作业的试验研究,以提高闭环控制系统的综合控制性能．