一种复杂环境中跳频信号检测和参数估计改进方法*

颜 雨，闫晓峰，吴治霖

（1.海军装备部，四川 成都 610036；2.中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引言

随着通信技术的迅猛发展，导致有限频谱资源越来越紧张。随着电磁环境中各种噪声和干扰的增加，如何在复杂的场景下正确、快速地完成通信信号分析与解调处理，已成为研究的热点课题。跳频信号由于其具有抗干扰性强、频谱利用率高、较难截获等特点，被广泛地应用在军事系统中，如美军的联合战术信息分发系统（Joint Tactical Information Distribution System，JTIDS）、SINCGARS系列电台、微波战术通信网、法国PR4G 系列电台以及民用GSM 移动通信、无线局域网等[1-2]。

跳频通信信号（Frequency Hopping Spread Spectrum，FHSS）是扩频通信信号的实现方式之一。跳频系统通常是由跳频频点序列发生器、频率合成器和同步器等共同构成的。跳频信号频率根据伪随机序列进行变化，接收机按照相同的参数与频率序列控制本振进行同步接收，最终完成解跳恢复原始信息。针对非合作条件下跳频信号的分析，研究人员开展了大量的探索，主要工作包括信号检测和参数估计等环节，但目前缺少对于在复杂环境如瑞利衰落信道中的处理方法。过去的一些思路参数估计精度不够，噪声环境适应能力相对较弱，而以前这类方法都是假设在白噪声的条件下进行的，普适性不理想。因此，研究如何克服复杂信道环境的影响，成功实现跳频信号检测和参数估计具有十分重要的意义。

对于非合作方，需要在缺少先验信息的条件下进行接收处理。在复杂电磁环境中，各种信号密集出现且易受到瑞利信道衰落的影响，导致过去许多思路效果不理想，对噪声环境的适应性较差，有待发展新的方法。针对此问题提出了一种基于滑动相关与小波变换结合的跳频信号检测和参数估计方法，核心思想是采用滑动互相关计算，并结合小波变换进行检测和参数估计的优化，适用于复杂电磁环境中的分析处理。该方法可较好地克服信道衰落和传播损耗的影响，检测性能良好，且跳频参数估计精度较高。

1 信号模型分析

首先对跳频通信信号模型进行说明。图1 给出了跳频系统的原理框图。

图1 跳频通信系统原理

跳频系统中可以使用各种调制波形，但由于频率不断变化，接收方一般采用宽带的非相干或者差分相干接收解调器。跳频通信中常采取FHSS/FSK和FHSS/PSK 调制方式。典型的FHSS/FSK 中实际接收频率fn可由式（1）计算得到：

其中，fLO表示本振频率，fHOP表示根据跳频PN 序列变化的跳频频率，且fD代表调制数据频率。典型的跳频信号时-频分布示意图如图2 所示[3]。

图2 跳频信号时-频分布

对于非合作通信中接收设备而言，由于没法获知跳频图案，为保证不丢失重要的信号，须采用宽带接收机接收所有频率信号[4]，再基于某些特征对信号进行检测、参数估计，完成跳频信号的分选。

2 检测与估计方法分析

针对复杂环境如瑞利衰落信道中对跳频信号的检测和参数估计问题，采取一种改进的基于小波变换与滑动相关处理相结合的算法思路。该方法的鲁棒性好，经过优化减小了计算复杂度，便于工程实现。

2.1 预处理

预处理包括下变频滤波、信号正交变换、中值滤波等，可以达到降噪的效果。首先对射频接收机的输出模拟信号进行ADC 采样。根据实际的跳频带宽，选取合适采样率的ADC 进行数字采样，将模拟信号转换为数字信号。需要注意的是，ADC 采样过程需要满足信号带通采样定理，即采样带宽必须大于或等于跳频信号带宽的两倍。

对经过数字采样的信号进行下变频和滤波处理。下变频的作用是为了将采样后的信号频率转变为检测和参数估计算法适于处理的信号频率，一般取值为跳频信号带宽的一半以上的频点位置。带通滤波的作用是进一步滤除背景噪声。该滤波器的带宽选取为等于跳频信号带宽值的1.5 倍。

信号的正交变换有利于对信号进行分解，可以更好地提取出各分量参数，利用Hilbert 正交变换可以得到信号的解析形式。经过接收机带通滤波器后的跳频信号可用数学表达式表示为：

其中，P表示信号功率，fn和θn分别表示第n个跳频载波的频率和相位，TH表示跳频时间，且αTH(0 ≤α≤1)表示第一跳信号与接收机本振时钟之间的定时偏差。带限噪声是一个标准正交的平稳随机过程，可表示如下：

其中ωc表示带通滤波器中心角频率。nI(t)、nQ(t)是独立平稳高斯过程，其均值为0，功率谱密度（Power Spectral Density，PSD）为，其中N0表示单边功率谱密度，WBF表示带通滤波器的带宽。因此，接收机的观测波形可表示为：

其中，h表示瑞利衰落信道的增益系数，其概率密度函数满足瑞利分布：

对于式（6），根据σ2易得出瑞利分布的衰落包络。其中，σ表示常数，且σ＞0；exp()表示指数函数；γ表示概率密度函数中的变量。

中值滤波对实际环境中可能存在的脉冲型噪声有良好的滤除作用，特别是在滤除噪声的同时，能保护信号的边缘使之不模糊。对信号序列xj（-∞＜j＜∞）进行中值滤波处理时，先定义一个长度为奇数的L长窗口，L=2N+1，N为正整数。设在某一个时刻，窗口内的信号样本为x(i-N)，…，x(i)，…，x(i+N)，其中x(i)为位于窗口中心的信号样本值。对这L个信号样本值按从小到大的顺序排列后，其中在i处的样值即为中值滤波的输出值。在实际处理过程中运用中值滤波去噪，滤波器阶数可选用32阶。可以使得相位包络形状从梯形变为半矩形，从而可使后续处理集中在跳频时间内[5]。

2.2 滑动相关检测

输入的采样信号经过滑动相关处理后的输出表达式为：

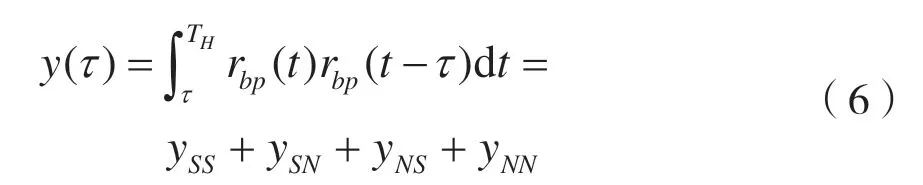
其中，ySS表示跳频信号sbp(t)与其自身的卷积分量，ySN表示跳频信号sbp(t)与噪声信号nbp(t)的卷积分量，yNS表示噪声信号nbp(t)与跳频信号sbp(t)的卷积分量，yNN表示噪声信号nbp(t)与其自身的卷积分量。在信噪比大于0 dB 时，ySN、yNS和yNN分量都约等于0，则输入信号的相关估计函数为：

其中，ωn表示信号功率采样的角频率。

相关处理后，信号的功率采样可定义如下：

相关峰值功率采样的计算式为：

其中LPF表示低通滤波器函数。此处的WM(k)，k=1，2，…，N先存储在长度为N的缓存中，相关函数的输出在每个跳跃点的结束时刻将减小。为了更好地检测出跳频信号是否存在，需要采用自适应判决门限（Threshold）作为联合检测算法的第一级门限，并易根据缓存输出的标准差计算推导得出，如图3 所示。

图3 跳频信号检测的互相关峰示意

为了进一步更好地抑制瑞利衰落信道中噪声影响，结合小波变换滤波器组增强检测性能。主要需要合理地选择一种良好的Harr 小波基，以适应于对跳频信号的分析[6]。本方案中采取的离散Harr 小波变换具有较优的时间-频率局部化特性，并给出其相应的计算表达式如下：

由于Harr 小波变换相对其他类型的时-频变换没有交叉干扰项，更适合于与滑动相关算法结合，是一种较佳的联合检测思路，可完成跳频信号的检测与参数估计。对跳频信号进行小波变换的同一个时间分析窗N内，在没有发生跳变的时刻，由于相邻平移因子对应的Harr 小波系数的时间相关性极高，导致每一时刻都要做变换。由于相邻的时间点做该变换存在极大的冗余时间，浪费了大量的计算时间，需要进行优化。先用滑动相关处理初步判定跳频信号的出现区域，再利用离散小波变换分多级进行跳频信号的精确搜索并获取频率值。在提取出信号特征后，对跳频信号的联合判决主要步骤说明如下。

（1）经过Harr 小波变换处理可得出一个转换矩阵，在该矩阵中选择最大值作为检测统计量ZN，将与后续步骤中计算得到的第二级门限ZT进行比较判断。

（3）对C给出一定确定度∂来判断平移因子的个数为多少，此处的确定度即为一个常数值的门限，用于数量判定，并不用于后续的代入与计算。

通过上述判决步骤，能够检测出跳频信号，还可以估计出跳变时刻。信号的检测概率Pd可根据式（12）进行推导计算：

其中R表示噪声矩阵观测量，与信噪比因素有关，计算式为，Pfa表示虚警概率。

2.3 跳频参数估计

先计算信号的瞬时相关函数，并利用Harr 小波系数进行分析和估计。跳频信号rbp的瞬时自相关函数定义如下：

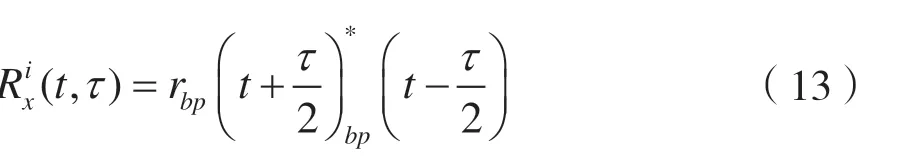
其中i表示提取的瞬时特征，t表示时间，τ表示延迟，即有，且 在τ=0 时 有，表示在t时刻信号rbp的瞬时功率。将信号划分为各小段，计算每个小段的瞬时自相关函数；瞬时相关函数关于τ呈奇对称。考虑到干扰项的因素，在计算实信号的瞬时自相关函数时，须采用Hilbert 变换得到信号的解析形式，如下所示：

继续求取式（9）的瞬时相关函数，可得：

小波变换算法的跳时估计精度较高，要求的阈值等于两个参数的乘积，一个是特征向量的方差，另一个是基于信噪比的估计[7]。在实际处理中，可先采用瞬时滑窗相关进行跳频信号的检测，再基于离散Harr 小波变换估计出信号参数，包括跳频周期、跳频频率和跳频时刻等参数[8]。

基于Harr 小波变换的思路说明如下。

（1）沿t轴对瞬时相关函数进行解卷绕，计算得出相位信息。相位解卷绕计算式可定义如下：

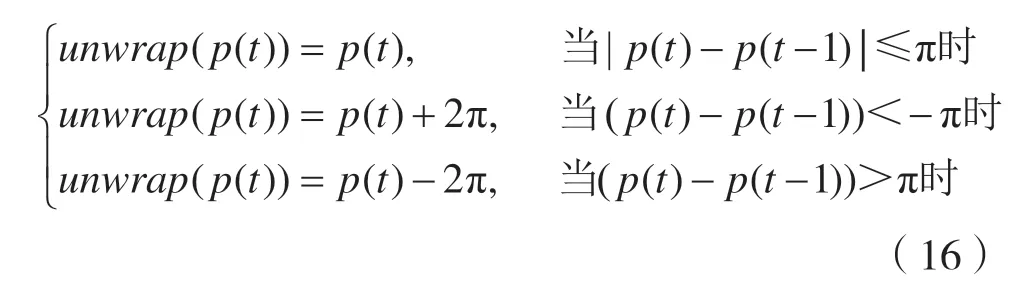
（2）再进行离散Harr 小波变换处理，将与两个第一尺度（离散Harr 小波变换分解得到的d1和d2）相关的小波系数相加；

（3）对全部的τ值都加上45°/135°，可得到新的估计特征向量，向量的索引对应于不同的跳频频率点；

（4）将该向量与特定阈值的方差进行比较，如果方差大于阈值，则在分段中存在跳跃点，与向量的最大值相关联的时刻位置点即为跳变时刻，跳变点之间的时间差则计算为跳频周期。

本方法中检测和参数估计算法的主要流程框图如图4 所示。

图4 改进的跳频检测和参数估计方法流程

3 仿真分析

下面对瑞利衰落信道中的跳频信号检测算法进行仿真验证。产生一段跳频信号，采样率为200 MHz，中频频率为60 MHz，Monte Carlo 仿真次数为1 000 次。设调制方式为MSK，单个跳频点信号的带宽为3 MHz，信道间隔为5 MHz，跳频周期为13 μs。信道为瑞利衰落信道，设定多径参数为存在两条路径，两条路径时延相差0.7 μs，其中一条路径的衰减大于另一路径2 dB。图5 为检测性能仿真曲线图，其中横轴表示信噪比，纵轴表示对跳频信号的正确检测概率。

图5 新方法和传统算法的性能曲线仿真曲线

再对瑞利衰落信道中的跳频信号检参数估计算法进行仿真验证，仿真参数如前所述，结果如图6所示，其中横轴表示信噪比，纵轴表示最小均方误差（Mean Square Error，MSE），用以衡量估计精度。

图6 新改进算法与过去算法参数估计性能仿真曲线

从图6 中可以看出，此处的改进方法性能更优且较稳定，是一种良好的对瑞利衰落信道中跳频信号的参数估计方法。

4 结语

在对抗环境中，信号调制样式越来越多样化，电磁环境也更复杂。本文改进方法采用了滑动相关结合小波变换进行分析处理，性能优越，可以在低信噪比情况下实现对跳频信号的正确检测和参数估计，且算法鲁棒性好，便于工程实现，实用性较强。今后还将进一步探索，为解决跳频信号盲处理问题提供一种更有效手段，对跳频信号监测和跳频认知接收领域的研究发挥更大作用。