一种改进的MRT 预编码方案*
2020-03-22姚红艳赵宏宇
姚红艳,赵宏宇
(西南交通大学 信息科学与技术学院,四川 成都 610000)
0 引言
2010 年底,美国贝尔实验室的科学家Marzetta T L 提出了大规模多输入多输出(Massive-Multiple-Input-Multiple-Output,Massive MIMO)系统时分双工的概念[1]。该系统能大幅度增加通信系统的通信速率,提升系统的频谱效率,但同时由于多用户信号之间存在干扰,如何消除这些干扰成为Massive MIMO 的主要问题[2]。预编码技术作为Massive MIMO 系统中的一项关键技术,可以解决多用户Massive MIMO 的干扰问题[3]。理论上,由于基站侧配置了大规模天线,所以简单的线性预编码即可消除用户间干扰。最常用线性预编码算法有最大比传输(Maximum Ratio Transmission,MRT)、迫零(Zero-Forcing,ZF)和正则迫零(Regularization-Zero-Forcing,RZF)预编码算法[4-6]。其中,MRT预编码通过对信道矩阵求共轭转置来获取发送预编码矩阵,避免了矩阵求逆,计算复杂度低,易于实现,但是频谱效率低;ZF 预编码算法通过对信道求取广义逆可以消除终端间干扰获得较好的系统性能,复杂度稍高;RZF 预编码可以取消噪声、信道不确定性能等因素带来的影响,获得很好的系统性能,但是无法推导系统性能的闭式表达式。
本文将MRT 和ZF 预编码结合,提出MRT 预编码的改进型线性预编码方案—Improved-MRT。在瑞利平坦衰落信道下,根据MRT 干扰信号的概率密度函数近似闭式表达式,进而分析Improved-MRT 中断概率、中断容量和频谱效率。仿真结果表明,相比MRT 预编码方案,改进的MRT 预编码方案能够同时服务更多的用户而不会产生中断,频谱效率也更好,并且得到的各个性能闭式表达式和实际仿真结果十分接近。
符号说明:大写粗体字母代表矩阵,小写粗体字母代表向量,大/小写不加粗字母代表标量,IN表示N×N的单位矩阵,|X|表示矩阵X的模值,tr(X) 表示矩阵X的迹,E[·]表示求变量期望,CN(μ,σ2)表示均值μ和方差σ2的循环对称高斯分布,{XH,XT,X*,X-1,X+}分别表示矩阵X的共轭转置、转置、共轭、逆处理、广义逆处理,表示X属于复数平面的M×N空间上。
1 系统模型
考虑单小区多用户Massive MIMO 系统,信道采用独立的瑞利平坦衰落信道,信道矩阵的元素服从CN(0,1)。假设基站端知道完美的信道状态信息(Channel State Information,CSI)。Improved-MRT预编码矩阵为MRT 和ZF 预编码矩阵的结合,其最终目的是在MRT 预编码的基础上增强期望用户的信道增益,从而达到增加系统频谱性能的目的,所以Improved-MRT 预编码矩阵为:

其中α为功率归一化因子,,Pt为发射功率,为噪声方差,代表信道矩阵,K是用户数,M是基站(Base Station,BS)端的天线数。
经过预编码后发射端发送信号可表示为:

其中s=[s1,s2,…,sK]T是K×1 的符号向量,sk表示k用户的符号,且与sj(j=1,2,…,K,j≠k)独立。每一个符号的功率归一化为1,即满足E[ssH]=IK。经过预编码后的发射信号仍然需要满足总的发射功率的限制,即为:

假设发送端和接收端都具有完美的CSI,那么接收信号向量为:

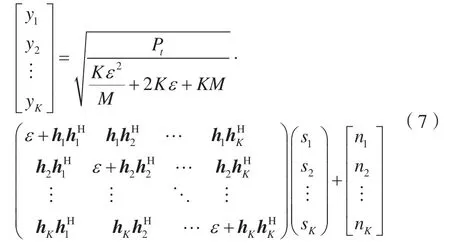
用户k的接收信号为:

那么,用户k的信干噪比SINR为:
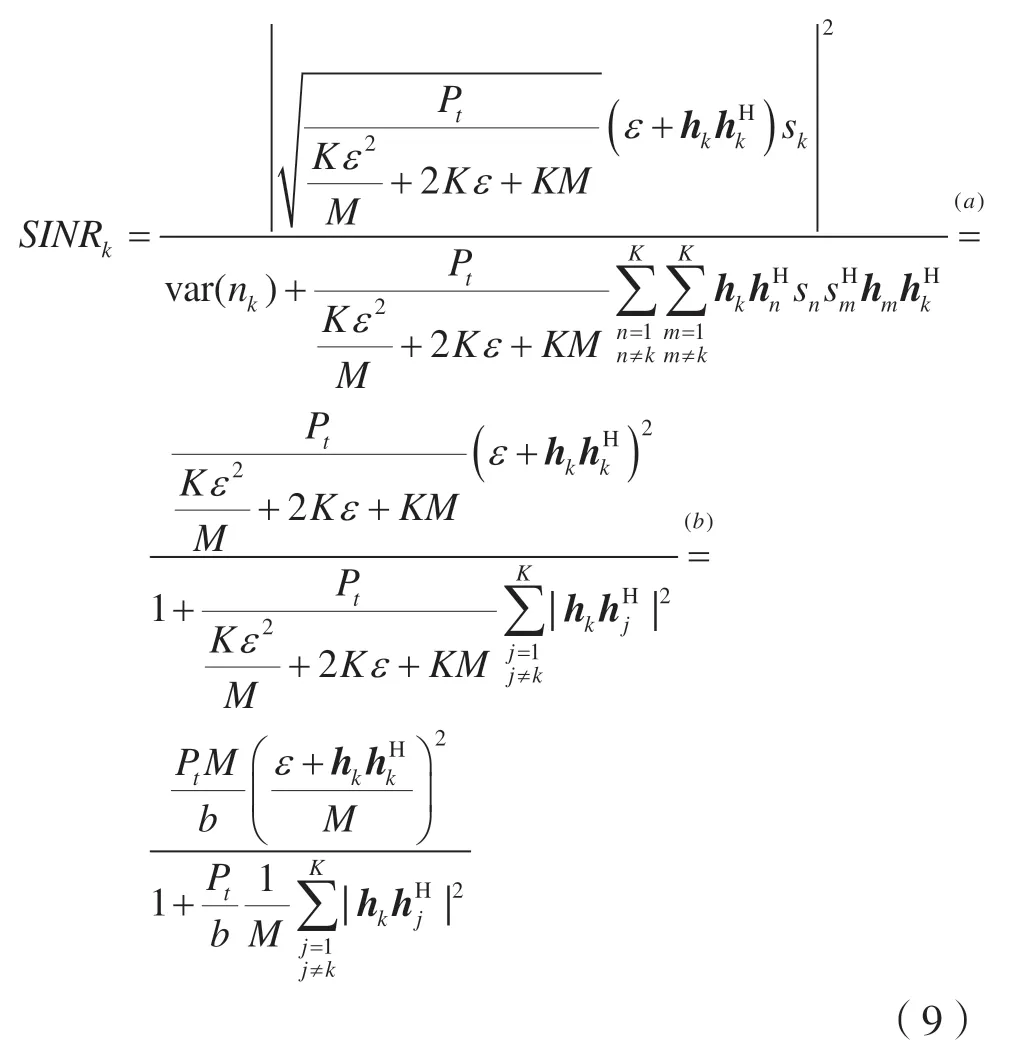
其中,(a)var(nk)表示变量nk的方差var(nk)=1,E[|sk|2]=1,(k=1,2,…,K),E[|sksjH|]=0,k≠j;(b)

2 Improved-MRT 预编码性能分析
在信道采用瑞利衰落信道的情况下,根据信道增益的特性得到MRT 预编码干扰信号的概率密度函数表达式[8],其中Improved-MRT 预编码的干扰信号和MRT 相同。通过该表达式得到系统的频谱效率、中断概率和中断容量,根据中断概率和中断容量评价一个系统可以同时服务的用户数。
2.1 系统干扰信号的概率密度函数
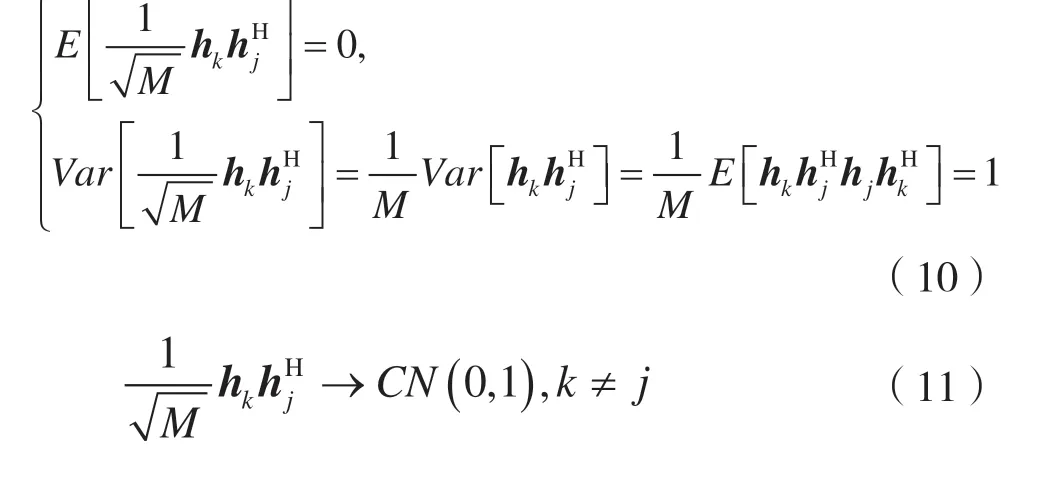
关系数为:

2.2 系统中断概率分析
化简用户k的信干噪比为:


其中o(1/M)表示高阶无穷小。当M趋于无穷时,只有第一项占主要的。Yk的方差可以根据其概率密度函数得var(Yk)=(K-1)(1+(K-2)/M),那么:

综上所述:当M→∞时,期望信号的方差趋于0,而干扰信号的方差与Pt和b有关,所以不能忽略Pt和b。当M→∞,干扰信号的方差大于期望信号的方差,即:


可以看出,尽管传输的总功率很大,中断概率也不会为0,与MRT 预编码的中断概率一致,得到中断概率可以有助于设计Massive MIMO 系统期望的中断水平,可以决定当给定rth值时大规模基站能同时服务的用户数。
2.3 系统频谱效率分析
当发射信号遵从高斯分布时,用户k的频谱效率为:


系统总的频谱效率为所有用户的频谱效率之和:

2.4 系统中断容量分析
中断容量的定义是用户处于非中断状态下的可达速率总和[12],表达式为:

3 仿真实验与分析
为了分析Improved-MRT 中断概率、中断容量和频谱效率的闭式表达式的拟合程度,本文采用瑞利平坦衰落信道模型,信道实现取1 000 次,对Massive MIMO 系统在不同基站发射天线数、不同用户数、不同发射功率下的性能进行全面分析,将Improved-MRT 与MRT 预编码的性能进行比较,并且验证本文推导出的中断概率、中断容量、频谱效率的近似闭式表达式的准确性。下面分别给出这3种性能的仿真结果。
3.1 中断概率仿真结果
图1 是发射天线数取100 和200 时不同用户下的中断概率图。当发射天线取100 中断概率超过10%时,MRT 服务的用户数为7 个,Improved-MRT 服务的用户数为8 个。当发射天线数从100 增加到200 时,MRT 比Improved-MRT 服务的用户数少4 个左右。所以,在Massive MIMO 中可以改善中断概率主要是由于大规模天线的原因。

图1 Pt=10 dB,rth=10 dB 不同用户的中断概率
图2 为基站配备不同天线的中断概率图。可以看出,M很小的时候,闭式表达式也能很好地接近真实的仿真图像。当总的发射功率为10 dB 时,Improved-MRT 需要120 根天线来达到10%的中断概率,而MRT 需要140 根天线才能达到同样的性能。当发射功率减少到7 dB 时,Improved-MRT 需要增加20 根天线就能达到同样的性能,MRT 仅仅增加10 根天线就能达到同样的性能。对于MRT 来说,改变总的发射功率,Massive MIMO 的中断概率没有特别明显的差异。
图3 是不同发射功率的中断概率图。随着总的发射功率的增加,系统的中断概率也不会趋于0,主要是由于MRT 和Improved-MRT 没有完全消除用户间干扰,但是Improved-MRT 随着总的发射功率的增加比MRT 的中断概率衰减得更快,主要是由于Improved-MRT 的期望用户的增益大,抑制干扰能力更强。当发射天线数为100 时,总的发射功率为15 dB,MRT 的中断概率为0.3,Improved-MRT的中断概率为0.05,所以Improved-MRT 的中断概率优于MRT。随着天线数增加到150,MRT 的中断概率保持到低于0.1 仅仅需要的发射功率为8 dB,Improved-MRT 的中断概率保持到低于0.1 需要M=100 的发射功率为13 dB 或者M=150 的发射功率为6 dB。可见,大规模的天线数比增加发射功率改变中断概率的性能更加明显。
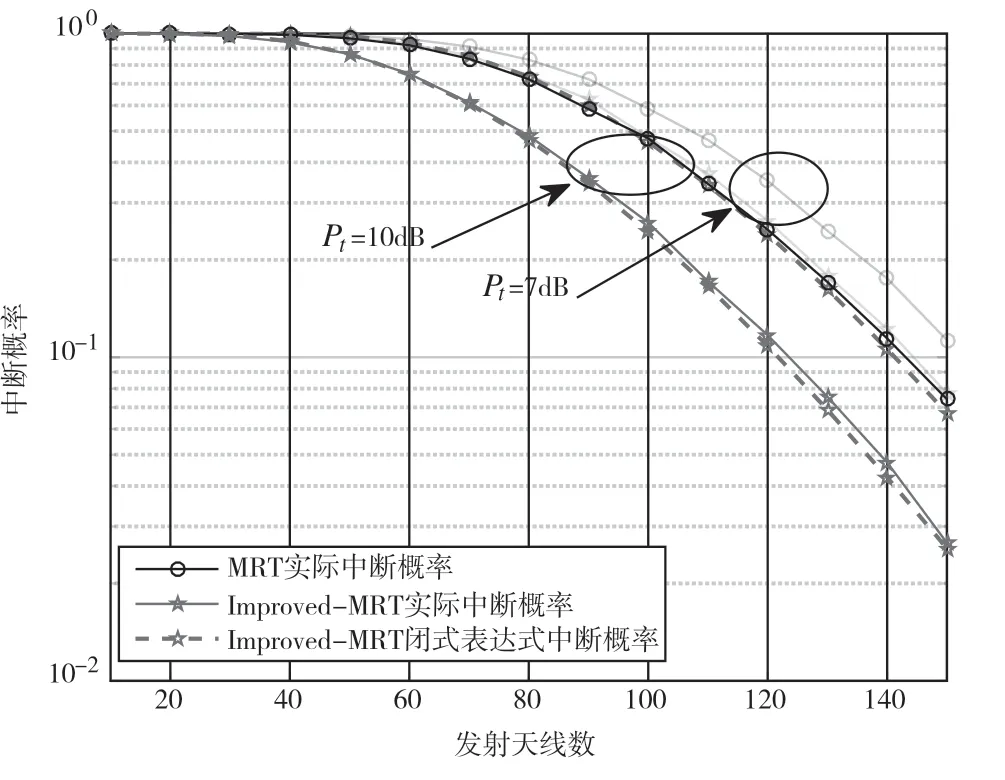
图2 K=10,rth=10 dB 不同发射天线中断概率
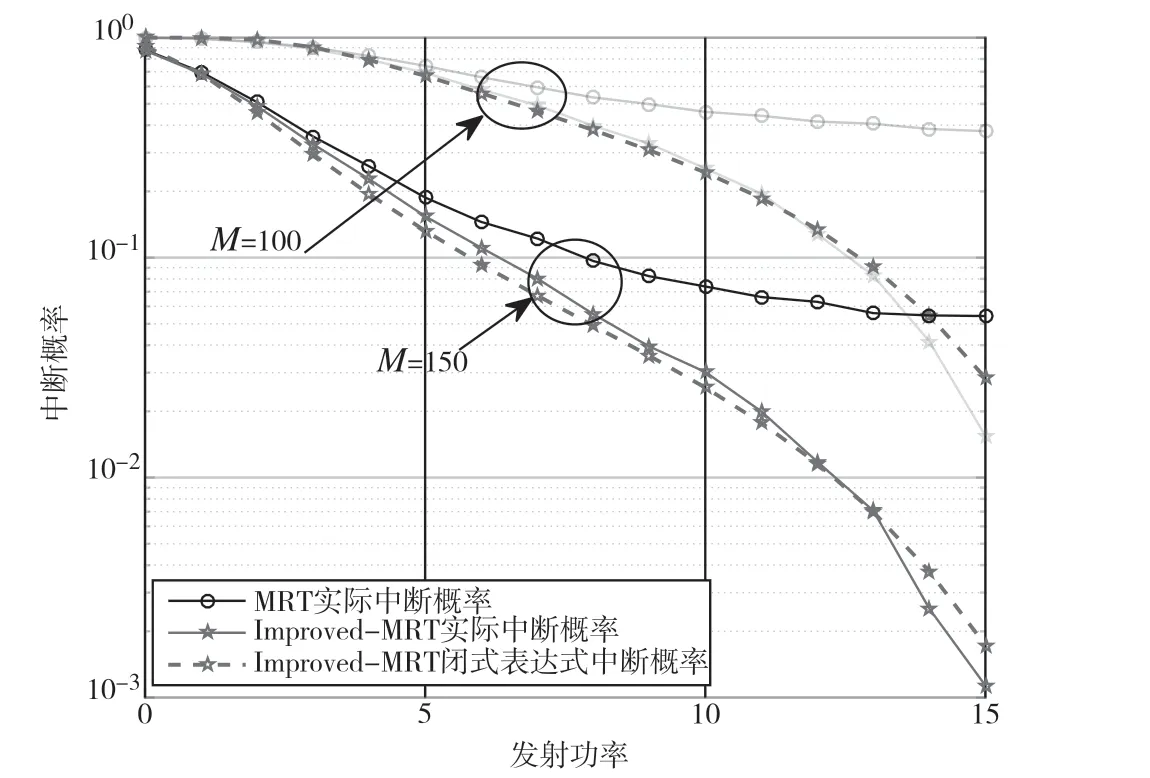
图3 K=10,rth=10 dB 不同发射功率的中断概率
3.2 频谱效率仿真
图4 显示了高信噪比情况下随着用户数的增加,系统的频谱效率增加。可以看出,MRT 预编码的频谱效率略低于Improved-MRT 预编码,且闭式表达式和实际的仿真结果十分接近,但是两者的频谱效率远低于ZF 预编码。究其原因,主要是ZF 预编码是假设完全抑制干扰的情况下得到的,这在实际信道中很难达到。
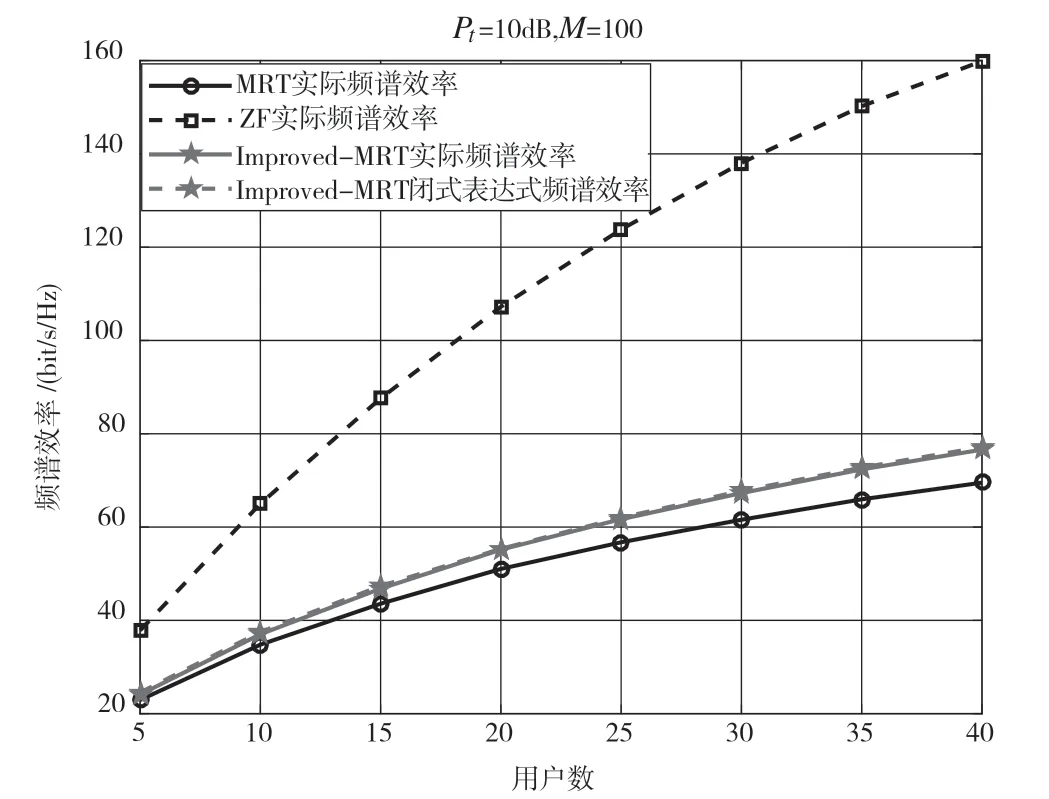
图4 高信噪比情况下不同用户的频谱效率
图5 为低信噪比情况下随着用户数的增加,MRT 和Improved-MRT 预编码的频谱效率不断增加。当用户数在5~25 之间时,ZF 预编码的频谱效率也是增加的;用户数在25~40 之间时,频谱效率逐渐下降,主要是由于ZF 预编码并未考虑噪声的影响,在低信噪比情况下,信道噪声占主要影响。当用户数较少时,系统可以保持较好的频谱效率。随着用户的增加,由于ZF 预编码用户数量过多会造成输出SINR 的严重下降,使得系统的频谱效率严重下降。

图5 低信噪比情况下不同用户的频谱效率
3.3 中断容量仿真
图6 为不同用户下的中断容量图。在很少用户数的情况下,随着用户的增加或者阈值的减少,中断容量增加。对于阈值取7 dB 时,Improved-MRT的用户数达到16 时中断容量开始下降,当用户数达到36 时,中断容量趋于0,所有用户处于中断状态;MRT 的用户数达到14 时中断容量开始下降,当用户数达到32 时,中断容量趋于0,所有用户处于中断状态。该图显示了中断概率的重要性。随着用户数K的增加,理论上总的频谱效率应该增加,但更多的用户会处于中断状态,所以实际系统的通吐量将会降低。
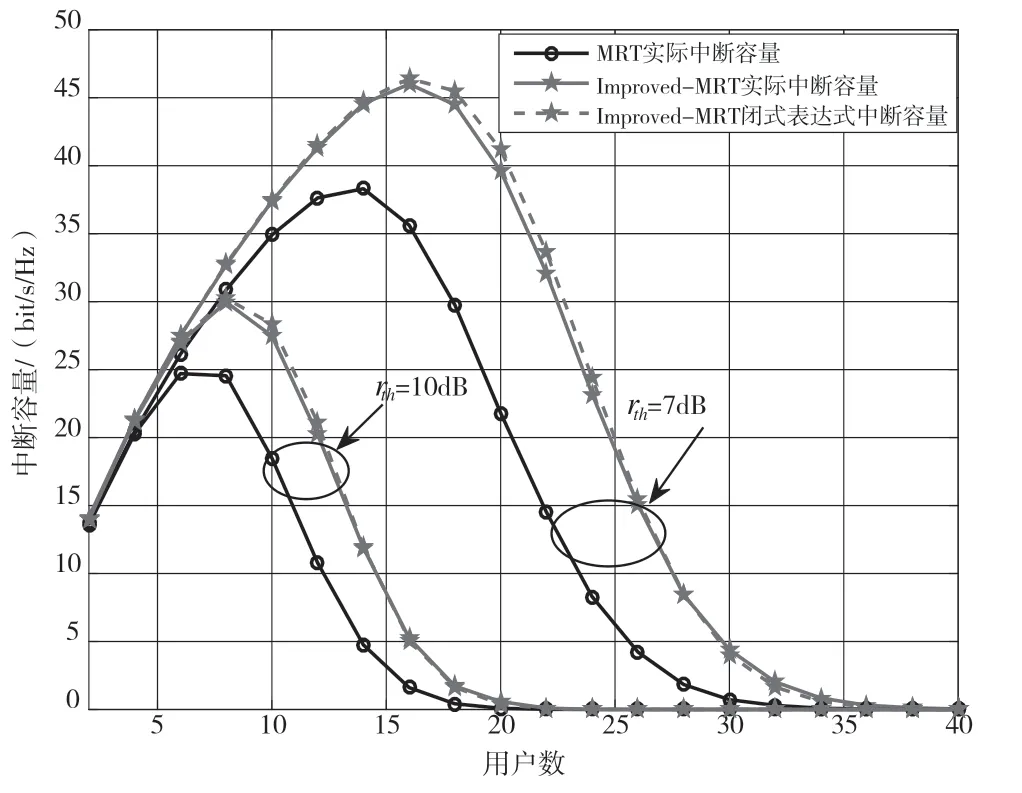
图6 Pt=10 dB,M=100 不同用户的中断容量
4 结语
本文根据MRT 预编码和ZF 预编码,提出了一种改进的MRT 预编码方法。该方法主要是在MRT预编码的基础上增强期望信号的信道增益,同时干扰和MRT 预编码的干扰大小一样,并且假设发射天线数很大或者趋于无穷,服务的用户数偏中等,根据中心极限定理,在瑞利平坦衰落信道中分析了该预编码的干扰功率,得到了干扰功率的概率密度函数的近似闭式表达式。通过比较信号功率和干扰功率的方差,将信号功率用其均值代替。干扰功率作为一个随机变量进行分析,得到了系统的频谱效率、中断概率和中断容量的闭式表达式,然后与理论仿真结果进行对比验证,可以得到闭式表达式,从而能够很好地拟合实际系统的性能。
随着用户数的增加,中断概率和中断容量的性能越来越差。所以,根据中断容量可以知道每个系统最多服务的用户数。由于Improved-MRT 是在MRT 基础上的改进,其性能比MRT 性能好,同时服务的用户数更多,中断概率更小,但是复杂度会有一定的提升,主要涉及到矩阵的求逆。针对矩阵求逆可以采用文献[13]中迭代的方法进行求解,使系统的复杂度减少。所以,总体来说,Improved-MRT 预编码的性能要优于MRT 预编码。
