低空气密度下的风力机叶片失速控制技术

刘 阳

(大唐新能源陕西公司,陕西 西安710065)

0 引言

近几年,随着可开发风资源区域的多样化,导致同一类型机组在不同环境下,运行状态存在较大差异。统计分析发现,风电机组运行在较低空气密度时,机组叶片根部在额定风速附近出现失速,导致机组满发功率风速向后推移,严重影响机组稳定运行[1]。

为了解决叶片在低空气密度下的失速问题,科研人员进行了一系列的研究。Butterfied[2]首次测量了水平轴风力机的压力分布,对动态失速进行了定量研究;Leishman[3]开发了能够描述动态失速翼型的升力,转矩和阻力特性的模型;由于风力机叶片失速发生在叶片根部,德国ENERCON公司对风力机叶片的根部采用了翼型段代替叶根的过度段和圆柱段,通过对叶片的改型设计,减小叶片根部的失速分离;邢作霞[4]、姚兴佳[5]等采用独立变桨技术以及智能控制算法等来降低机组载荷,减少叶片失速。刘庭瑞[6]针对风力机叶片失速振颤断裂失效问题,采用最优模糊比例积分微分(proportional integral derivative,PID)控制方法和径向吉函数神经网络PID控制方法进行分析,为风力机叶片失速非线性气弹变桨提供了新思路。陈岩[7]通过对风力机叶片翼型进行稳态气动力分析,改善了失速工况下的负阻尼。俞国华[8]通过数值计算与理论分析研究了风力机静态失速和动态失速问题,对理解失速的复杂流动机理提供了参考。

本文在前人研究的基础上,针对叶片在低空气密度下,额定风速附近失速问题,分别采用提前变桨策略以及叶片根部加装根箱两种解决方案,并采用三维数值模拟对这两种方案进行验证,通过对这两种方案的对比分析,得出解决叶片失速的最优解决方案。

1 风力机叶片失速理论分析

1.1 翼型失速理论分析

风力机叶片翼型的攻角α为来流风速方向与叶片翼型弦线之间的夹角。由图1可知,叶片翼型截面的相对速度vrel为风轮平面的轴向速度(1-α)v0和切向速度(1+α')ωr的合成,并且攻角α可由vrel和旋转平面之间的夹角φ与桨距角θ表示,即：α=φ-θ。

图1 叶片截面翼型图Fig.1 Blade Section Airfoil Diagram

根据在翼型上升力阻力的定义,得到单位长度上的升力L和阻力D为：

式中：ρ为空气密度,kg/m3;c为叶片弦长,m;Cl为升力系数;Cd为阻力系数。

由公式(1)(2)可知,翼型的升力和阻力除与来流风速以及空气密度有关外,还与Cl和Cd有关,且不同的翼型具有不同升阻力系数,典型的Cl和Cd曲线如图2所示。由图2可知,当攻角大于aM后,升力系数逐渐减小,阻力系数逐渐增加,从而导致升力迅速下降,阻力迅速上升。aM点称为“失速点”,翼型在经过失速点后,出现失速[4]。

1.2 低空气密度下风力机叶片失速

目前,主流的风力机为变桨变速型风力机。变桨变速型风机在额定风速以下时,风力机组桨距角始终维持在最佳桨距角(一般为0°),通过控制风轮转速来调节功率;额定风速以上,通过不断调整攻角避开其失速点以维持额定的功率输出。并且同一台风力机在相同的最优桨距角情况下,空气密度不同,对应的功率曲线不同。

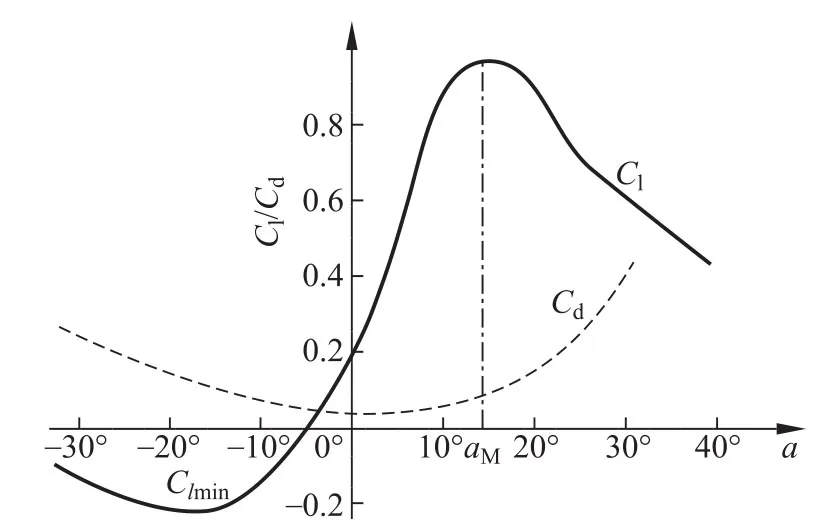
图2 Cl和Cd随功角变化曲线Fig.2 Curves of Cl and Cd varying with work angle

风力机组在实际运行过程中,空气密度越低,要达到额定功率,需要的来流风速越大。而额定风速前,风轮转速已达到额定转速保持不变,随着来流风速的增加,φ角增加,但θ保持不变,从而α不断增加,导致叶片攻角达到并超过失速点,引起叶片失速。图3为空气密度为1.2 kg/m3变化至1 kg/m3时的功率曲线,由图3可知,在空气密度变化至1 kg/m3,风力机功率曲线在13 m/s附近,明显发生拐点,此点为失速点。

图3 不同空气密度下的功率曲线Fig.3 power curve under different air density

2 风力机叶片失速控制方案

2.1 叶片失速最佳桨距角调节方案

在低空气密度下,为了避免风力机在额定风速前失速,可采取提前变桨控制策略,通过增大桨距角,达到减小叶片攻角,控制叶片失速的目的。同时,为了避免叶片自身将造成较大的风能损失,根据如图4所示的在不同桨距角下的Cp-λ曲线可知,同一叶尖速比下,桨距角越大,风能利用系数越低。因此综合考虑,变桨角度最大不能超过2°。

图4 在不同桨距角下的Cp-λ曲线Fig.4 Cp-λcurve at different pitch angles

为了对变桨效果进行验证,利用Bladed软件,对所研究的1.5 MW机组,在空气密度1 kg/m3,变桨角度分别为0°、0.5°、1.0°、1.5°以及2.0°情形下的功率曲线进行模拟,得到功率曲线如图5所示。

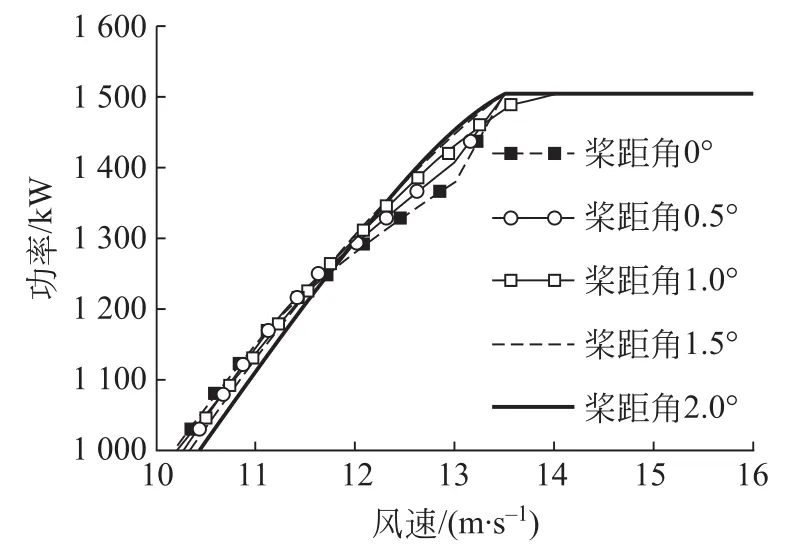
图5 不同桨距角下静态功率曲线Fig.5 Static power curves at different pitch angles

由图5可知,桨距角为0°时,风速为13 m/s附近时,风力机组功率出现拐点,此点为叶片的失速点。随着桨距角在0°到2°的变化过程中,风力机功率曲线拐点明显变平滑,其功率值提高。

2.2 叶片根部加装根箱

根据经验,风力机发生失速的区域为叶片的叶根段,除改变桨距角外,风力机叶片通过叶根改型,在物理上阻断叶根的流动分离,可有效控制叶片的失速。学者们已经通过将叶片根部圆柱度和过多段改为翼型段来增加功率捕获减小失速分离,但其改善失速分离效果并不明显,本文在其基础上,将叶根圆柱段改为翼型段,同时加装了翼刀结构,其结构如图6所示。

由图6可知,叶片结构改型方式为：叶片根部改型为在叶片展向0.04R～0.25R(R为叶片长度)区域内,保持叶片前缘形状不变,在后缘加装增功组件,将原叶根的圆柱段改为翼型段,同时加装翼刀。其翼型形状为原叶片在最大弦线位置处的翼型,扭角大小与原叶片在同位置处的扭角相等。第1个翼刀距离叶根约2 m。

图6 风力机叶片根部改型结构Fig.6 Wind turbine blade root modification structure

3 计算模型建立

3.1 模型建立

本文根据风电机组的性能及尺寸建立计算模型,对两种方案进行验证。计算区域分为旋转域和静止域。旋转域为包含叶片在内旋转部件。静止域为包含塔筒,机舱等在内的静止部件。计算模型图如图7所示,计算域长、宽、高分别为8倍风轮直径、3倍风轮直径、3倍风轮直径。

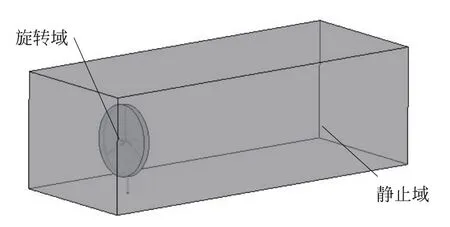
图7 风电机组计算模型Fig.7 Model of wind turbine calculation

风电机组基本参数为：额定功率1.5 MW,叶片个数为3个,叶片长度43.5 m标准空气密度下的额定风速12 m/s,额定转速为17.6 r/min,风轮仰角为5°,风向为上风向。

3.2 网格划分与无关性验证

运用ICEM软件对风力机计算流域按区域进行结构网格划分,如图8所示为划分好的风力机网格。为了确保叶根区域的计算精度,对叶片根部进行网格加密,改型后根部网格如图9所示。

数值模拟中,为了消除网格数对计算结果的影响,分别对698万、867万、1 078万、1 244万和1 479万网格数的模型进行了模拟,如图10所示。由图10可知：随着网格数的增加,计算功率逐渐稳定。在网格超过1 124万后,功率的变化很小。综合考虑模拟精度和计算时长的影响,最终确定网格总数为1 124万,根部改型后的网格为1 346万。

图8 风力机轮毂周围网格Fig.8 Grid around wind turbine hub

图9 改型后叶片根部网格Fig.9 Modified blade root mesh

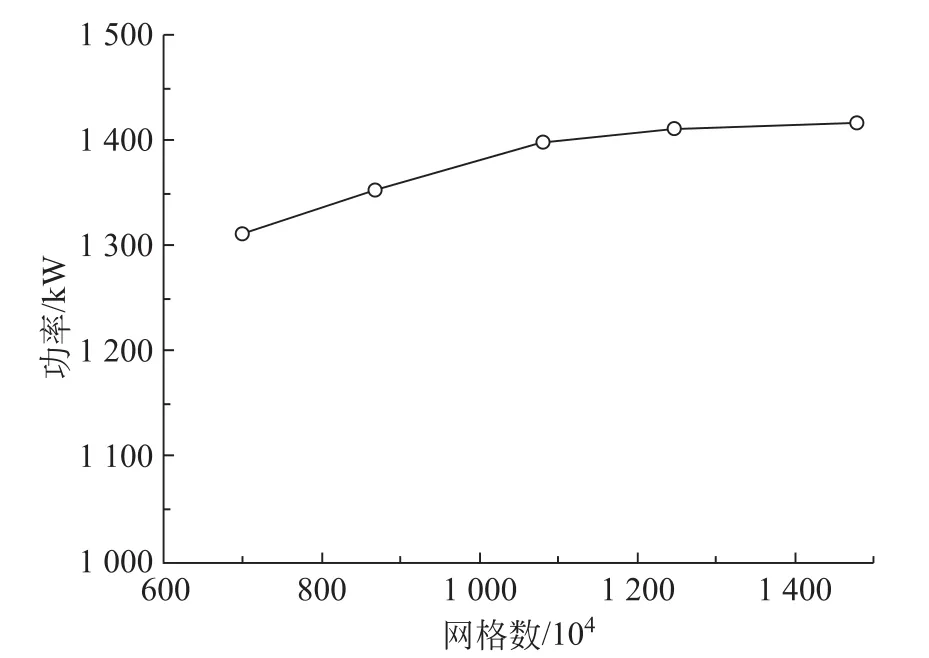
图10 网格无关性验证Fig.10 Grid independence verification

3.3 计算方法和边界条件设置

计算域入口处的来流风速,出口的相对压力设定为0,交界面采用动静转子边界,地面、叶片表面、塔筒、机舱和导流罩均采用无滑移壁面。计算软件为ANSYS CFX,湍流模型采用对壁面的流固分离具有很高的计算精度的SSTk-ε模型。对流向采用高阶精度格式,隐式求解,同时,对风力机的功率和效率进行监测,当功率和效率误差小于5%且平均残差小于10-4时认为收敛。

4 计算结果分析

4.1 功率分析

通过对机组运行数据的统计分析得知：风速在13 m/s时,叶片的流动分离最大。同时综合bladed分析结果,本次分析在13 m/s风速,1 kg/m3空气密下,分别对原叶片桨距角为0°、1.5°以及根部改型叶片在0°桨距角进行模拟。

表1所示为各计算工况下的风力机组功率,由表1可知,叶片在改变桨距角后,功率增加越1.84%,叶片根部改型后,功率增加2.14%。

表1 功率随桨距角变化表Table 1 Variation of power with pitch angle

4.2 叶片根部表面流线分析

在风力机旋转叶轮的作用下,气流在通过叶片前缘位置后,流动速度开始增大。由于空气的粘性作用,当气流速度达到最大值后,叶片吸力面的气流速度逐渐减小,同时,逆压梯度逐渐增加,当吸力面上层流动无法克服逆压梯度时,将在叶片吸力面上发生倒流或逆流,使得气体在吸力面上发生分离[9-11]。气流的分离会造成大量的紊流和涡,使升力大量受损。同时,气流分离越靠近前缘位置,所产生的压差阻力会越大,对气动性能影响越明显。风力机在运行过程中,叶片根部吸力面上产生的流动分离不可避免,因此,有效的减小叶根气流分离,能够显著提升叶根的风能捕获。

图11 叶片表面极限流线分布Fig.11 Distribution of limit streamline on blade surface

由图11可知,来流风速为13 m/s(桨距角β=0°)时,从叶片根部起始位置开始便出现了气体的流动分离。同时形成了一条清晰的分离线,沿着叶片展向,分离线逐渐向后缘位置靠近,在展向约0.25R位置处时,分离线在叶片后缘位置处消失。来流风速为13 m/s(桨距角β=1.5°)时,对比β=0°,桨距角增加,叶片吸力面上流动分离线在叶根的起始位置远离前缘位置,且叶片根部的分离区域变小;叶片根部改型后,来流风速为13 m/s(桨距角β=0°)时,叶片根部流动分离的起始位置与原叶片相同。但叶片表面流动在接近第1个翼刀之后沿展向消失,有效控制了叶片。

由上分析可知,改变桨距角与叶根改型均能减小叶片根部的流动,但根部改型的效果更为明显,改变桨距角仅减小了叶片表面流动分离。而叶片根部改型后,虽使根部出现了较小的附着涡,但显著改善了叶根区域的流动分离,有效地将叶片根部的流动分离控制在第1个翼刀叶根侧。

4.3 经济性分析

从分析结果可知,通过调节桨距角来控制叶片的在低空气密度下的流动分离,仅需要对机组的主控制程序进行修改,无需在机组上增加其他硬件设备。而针对叶片根部改型,需要在设计阶段对叶片进行优化改型,对于已建成风场需要很大的技改费用,因此针对低空气密度下的叶片失速问题,已建成的风场易采用调节桨距角解决,而针对未建设风场,采用根部改型后的效果更好。

5 结论

针对低空气密度,风电机组在接近额定风速附近运行,叶片根部出现失速问题,本文提出了提前变桨策略以及叶片根部加装根箱两种方案解决方案,同时采用三维数值模拟对两种方案进行验证。得到如下结论：

(1)采用两种方案均能减小叶片表面失速分离,但加装根箱的改善失速分离的效果更为明显。

(2)采用提前变桨控制策略可提升机组功率约1.78%,叶片根部加装根箱可提升机组功率约2.14%。

(3)对于已建成的风场,从经济型考虑,采用提前变桨控制策略解决叶片失速问题效果更好。