磁耦合谐振式无线能量传输技术效率分析

（国网浙江省电力有限公司宁波供电公司，浙江 宁波 315010）

0 引言

无线能量传输是利用某种介质（电磁场、激光、超声波等）替代导线进行能量传递的一种技术。无线能量传输技术由于采用非接触式传输能量，弥补了传统直接接触式能量传输方式的弊端，具有很多优点。

近几年，随着新的研究方法的应用及新理论的突破，无线输电技术越来越受到人们的关注。文献[1]介绍，2007 年7 月6 日，基于电磁谐振原理成功地“隔空”点亮了离电源2 m 多远处的一个60 W 灯泡。在该实验中，发射器发射的能量有40%～50%传输到负载，无线传输装置工作的有效距离最远达到2.74 m。实验的依据是2 个具有相同谐振频率的物体能够耦合，而与环境中的其他非谐振物体的相互作用很小，它的理论分析框架是“耦合模理论”。通过理论与实验验证，实现了中距离高效率的无线电能传输，这引起了全球的广泛关注，再一次掀起了对于无线电能传输技术的研究热潮。

目前，根据无线能量传输原理，可将其按传输方式分为三类[2-7]：电磁感应式无线能量传输技术、辐射式无线能量传输技术和磁耦合谐振式无线能量传输技术。

而新型的磁耦合谐振式无线能量传输技术是利用2 个具有相同特定谐振频率的电磁系统在相距一定的距离时，由于电磁耦合产生谐振，进行能量传递。一般来说，2 个有一定距离的电磁系统，相互之间是弱耦合；但若2 个系统的固有谐振频率相同，则会产生强磁谐振；如果一方不断为系统提供能量，而另一方消耗能量，则实现了能量的传输。由于采用共振原理[8-9]，与共振系统以外的物体之间相互作用很小，所以磁耦合谐振式无线能量传输技术是世界上无线输电领域的前沿课题。虽然目前国内外无线电能传输系统的产品已进入产业化阶段，但远距离、大功率以及高效率的产品尚处于基础理论和实验研究阶段，若能研究出集安全、远距离、大功率及高效率于一体的传输装置，则该技术应用前景将会更加巨大。本文主要研究基于磁耦合谐振的无线能量传输系统基本原理并建立无线能量传输的系统模型，确定数学模型，推导出系统效率表达式；通过MATLAB/Simulink 仿真讨论系统传输效率的影响因素，为后续实验研究提供一定的参考。

1 磁耦合谐振式无线电能传输系统建模

线圈的等效电路是建立系统等效电路的基础。本节建立通入高频电流后的线圈等效电路模型，并确定各参数的计算方法，从而建立系统等效电路。

1.1 线圈等效电路

设线圈匝数为N，线圈半径为r，线径为a，当其中通过角频率为ω 的交流电时，可将其等效为如图1 所示的电路[10]。

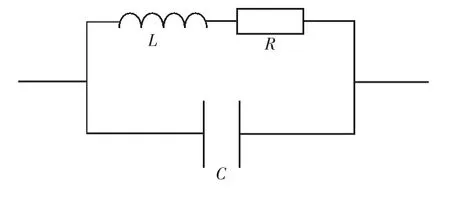
图1 线圈等效电路模型

线圈的电参数可分为电感量L，线路损耗R以及分布电容C。其中以电感量为主要参数，在实际应用中要尽量减小损耗R；分布电容往往较小，只有在较高频时才较为显著。在采用集总参数进行计算时，也可将图1 的电路简化为电感与电阻的串联电路。

改变线圈形状（如方形、螺旋形等）、匝数、线圈材质以及线径，即可改变等效电路中的各参数，同时影响到交流电产生的磁场分布，其等效电感与等效电容根据电磁理论可分别通过式（1）、式（2）计算[11]：

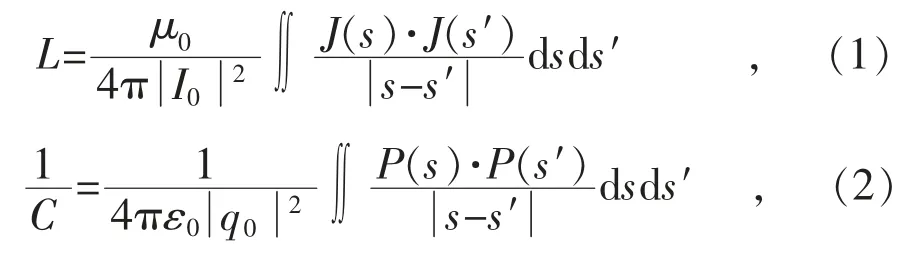
式中：μ0为真空磁导率；J（s）和J（s′）分别为场点和源点的空间电流密度；P（s）和P（s′）分别为场点和源点的电压密度；ε0为真空介电常数；s 为场点到坐标原点的距离；s′为源点到坐标原点的距离；I0为电流强度；q0为点电荷。但是利用这种方法往往难于计算，对于特定形状线圈可通过经验公式进行简化运算。本文仅对多匝圆形线圈进行各个参数的计算。

对于N 匝线圈可通过式（3）计算电感：

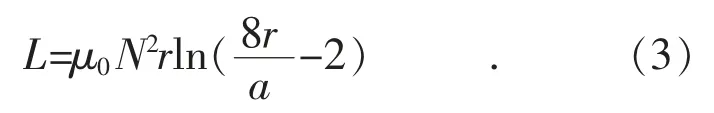
对于高频下的线圈而言，电路中电阻可分为两部分，一部分是电流流经线圈时发热造成的电阻热损耗；另一部分是交变电流产生交变电磁场，类似天线一样，线圈会向外辐射电磁能，造成能量损失，此损耗亦可通过阻抗形式表现计算，称为辐射电阻。

考虑到集肤效应，损耗电阻计算表达式为[12]：

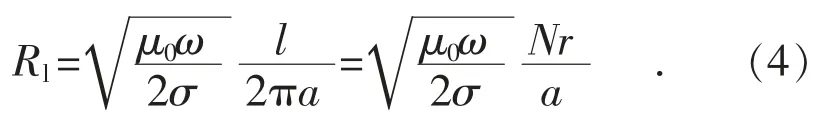
辐射电阻计算表达式为[11]：

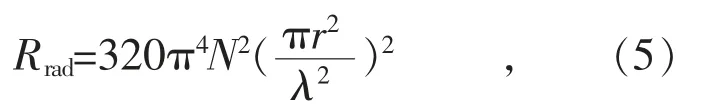
式中：σ 为电导率；λ 为电磁波波长；l 为线圈长度。取N=4，r=0.2 m，辐射电阻Rard=97（f/108）4，当f=1 MHz 时，Rard=0.97×10-6Ω；当f=10 MHz时，Rard=9.7×10-3Ω；当f=50 MHz 时，Rard=6 Ω；当f=100 MHz 时，Rard=97 Ω。可见，频率越高，线圈的辐射性越大，所以在通信领域，一般频率都很高。由于本系统在实际运行中频率范围为1～10 MHz，辐射电阻非常小，因此相对线路损耗电阻往往可以忽略[13]。

1.2 系统等效电路

在2 个线圈形成的共振系统中，通过磁场共振，可以实现线圈之间的能量传递。利用线圈的电感与分布电容或是外加电容可以形成谐振回路。发射线圈与接收线圈设计为相同结构，即使参数不完全相同，通过电容补偿，接收线圈的自谐振频率与发射线圈也保持一致。发射装置与接收装置中电感与电容均可为串联谐振或并联谐振电路。

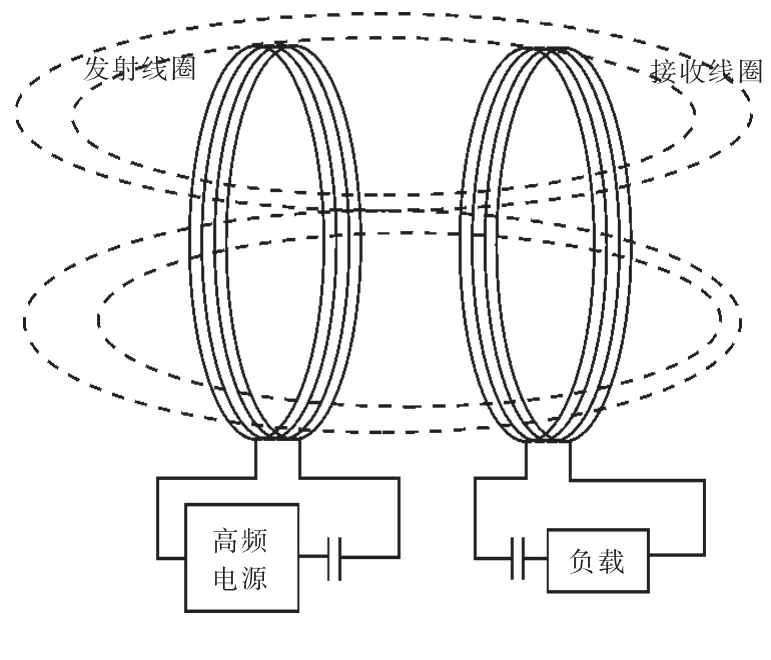
图2 串联模式的磁场谐振耦合系统

串联模式的磁耦合谐振式无线电能传输装置系统模型如图2 所示。其中，高频电源产生与发射装置所需的谐振频率相同的正弦电流，并向发射装置提供能量。高频电流流经发射线圈时，在其周围产生与电流相同频率的交变磁场，从而在接收线圈中感应生成相同频率的电流。由于接收线圈的自谐振频率与产生的感应电流频率相同，从而接收线圈发生自谐振，同样在接收线圈周围产生交变的磁场，此磁场与发射线圈产生的磁场叠加，两线圈之间通过磁场建立耦合关系，发射线圈与接收线圈形成共振系统，能量由发射线圈源源不断传递到接收线圈，为了保证磁场可以尽可能穿过接收线圈，两线圈应同轴。

由于本文中关注的是能量从发射线圈到接收线圈之间的转换效率，不考虑电源部分的损耗，因此在下面的分析中，将电源假想为理想电源，无损耗，那么就可以将系统中的功率分为3 部分：发射端的损耗功率PT，接收端的损耗功率PR，负载消耗功率PL，由此可以得出系统传输效率表达式为：

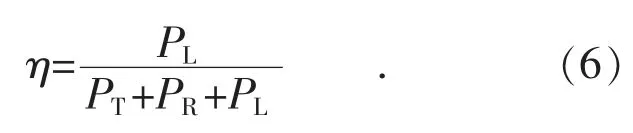
式（6）适用于各种耦合系统，由式（6）可知，提高耦合系数与损耗率的比例，有助于提高系统传输效率，但并不能得出影响效率的具体因素。下面从等效电路模型着手对其效率进行深入分析。

首先建立系统的等效电路模型[14]。1.1 小节已建立单个线圈模型，为便于计算，在以下分析中，采用集总参数，不考虑杂散参数，因此线圈等效为一个电感与电阻的串联，通过外加电容形成谐振电路。本系统利用共振原理使发射线圈、接收线圈达到自谐振。其等效电路模型如图3 所示。

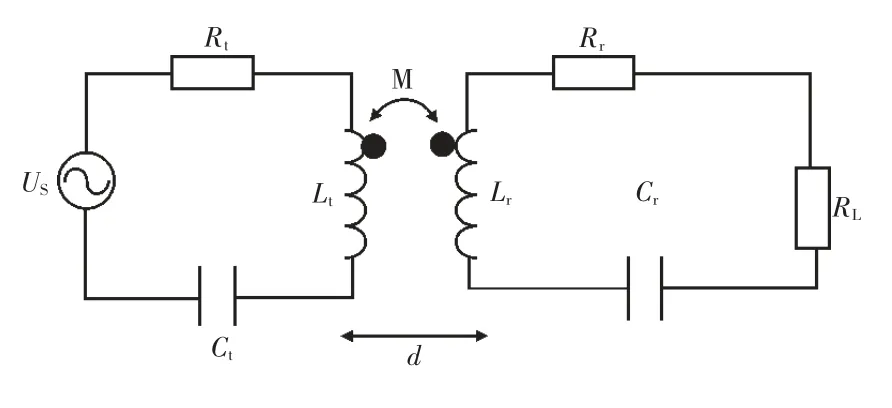
图3 等效电路模型

图3 中，US表示高频电源；Rt，Rr分别为发射线圈、接收线圈等效电阻；Lt，Lr为分别为发射线圈、接收线圈等效电感；Ct，Cr分别为发射线圈、接收线圈等效外加电容；RL为负载电阻；d为两线圈之间的距离。

1.3 系统传输效率的影响因素

设发射线圈、接收线圈匝数分别为nt和nr，半径分别为rt和rr，两线圈各参数可一致，也可不同。

发射线圈与接收线圈阻抗分别为：

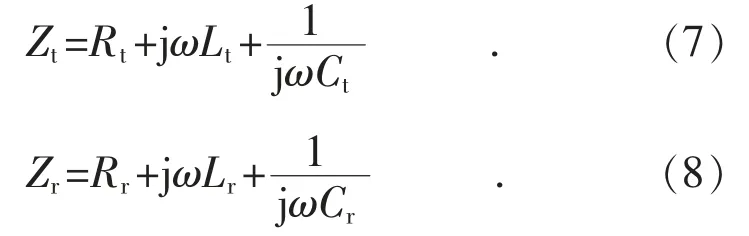
两线圈之间会产生互感，轴心线同轴时其值可近似计算为[15]：

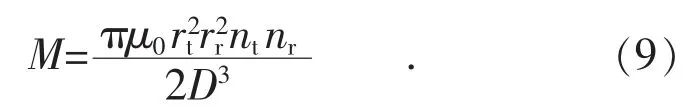
当线圈参数一致时，rt=rr=r，D=。

由此可计算两线圈中电流：

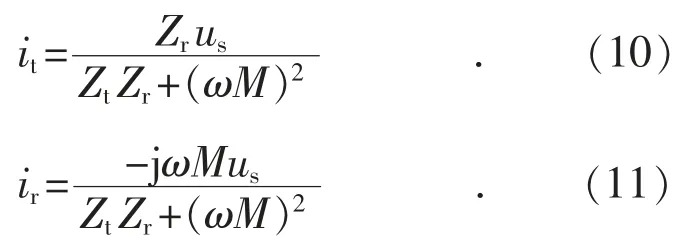
进一步可得到效率计算表达式：

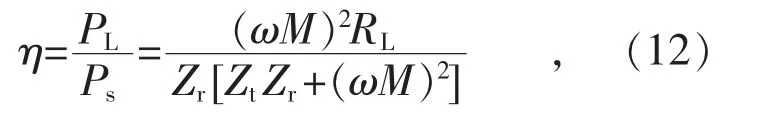
当两线圈发生共振时，因为各个线圈自谐振，可得：

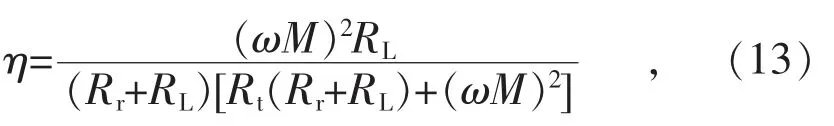
下面就从多个方面分析影响效率的因素，为便于分析，以下的运算中，认为发射线圈、接收线圈各参数一致，即Rt=Rr=R0。假设线圈参数、电流频率与传输距离保持不变，则存在唯一变量RL，很容易求得最大效率条件：

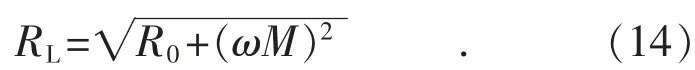
此时最大效率表达式为：

最大效率条件也称为阻抗匹配，最优阻抗值取决于线圈阻抗损耗以及互感、频率的大小，可见，在R0较小而ωM 较大即强耦合时，其最大效率可接近100%。通过对线圈选用合适的材料、尺寸，线路损耗R0往往相对负载较小，因此效率表达式可进一步近似为：

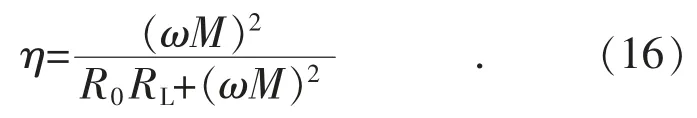
将互感表达式带入式（16）可得：

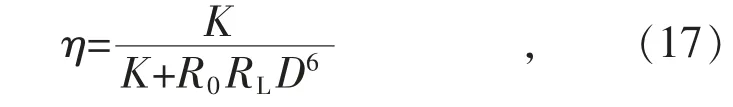
由式（16）、式（17）知，除负载之外，影响系统效率的因素主要有系统频率、线圈匝数、线圈半径、线圈线径（线圈损耗电阻）以及传输距离[16-17]。下面分析每个因素的影响效果[18-19]。

（1）由式（16）可知，当负载相对线路损耗较大时，负载电阻越大，系统的传输效率越低。

（2）随着传输距离d 的增大，耦合系数减小，传输效率也降低。D6=r6（1+d2/r2）3，固定线圈半径不变，改变传输距离。当d/r=1 时，D=8r6；当d/r=2时，D=125r6；当d/r=3 时，D=1 000r6。可见，随着传输距离的增加，尤其在传输距离为半径的2 倍之后，距离的变化会对效率产生较大的影响。

（3）当频率以及距离一定时，对效率影响较大的参数就是线圈的线径以及匝数。线圈的线径主要影响线圈损耗电阻，受集肤效应的影响，线圈中电流主要分布在线圈表层，线径越大，线圈截面积越大，损耗电阻越小。由式（17）可知，K值的大小与匝数的4 次方、半径的8 次方成正比，这2 个参数的变化会明显改变K 值，继而影响效率。可见，增加线径和匝数是最为有效的提高效率的办法。

（4）由式（17）可知，提高系统频率也有利于提高传输效率。对于串联线圈模型，其固有谐振频率值取决于线圈等效电感以及外加串联电容，其关系为f0=1/2π，所以对于不同的线圈，可以利用不同的外加补偿电容来实现频率的一致。

（5）从效率表达式中不能明显地看出线圈位置对于系统传输效率的影响。基于磁耦合谐振的无线能量传输依靠的是磁场这一介质，这个磁场由发射线圈与接收线圈共同产生的。由于磁场不是均匀分布在空间中，2 个线圈的位置必然影响到系统的传输效果。对于圆形线圈，磁场主要分布在线圈中心轴线上，因此，发射线圈与接收线圈平行同轴更有利于能量的传输。

2 MATLAB/Simulink 仿真分析

2.1 负载大小对效率的影响

由式（16）可知，负载电阻相对线路损耗较大时，负载电阻越大，系统的传输效率越低。现利用MATLAB/Simulink 对负载变化时的系统进行仿真，分析其效率，验证理论分析的正确性。

取线圈半径r=20 cm，线径a=1.4 mm，线圈匝数N=4，外加电容C=1.0 nF。

根据式（3）—式（5）和式（9），计算得线圈电感值：

线圈损耗电阻：

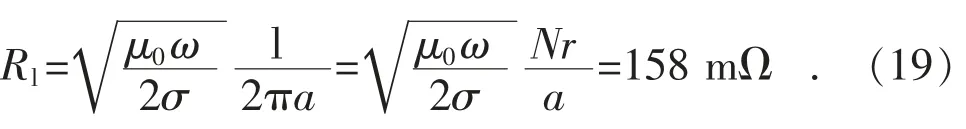
辐射电阻：

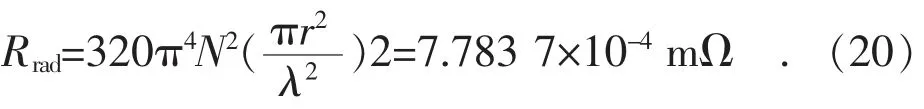
接收线圈与发射线圈之间的互感：

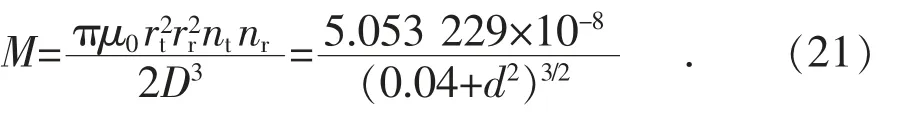
由此得到不同传输距离d 对应的M 值，如表1 所示。

表1 不同传输距离d 对应的互感M 值

由ω0=得电源频率f=0.945 9 MHz，仿真电源电压峰值取100 V。

当传输距离d=30 cm，负载RL变化时，系统传输效率η 的理论值和仿真值如表2 所示，转换成效率曲线如图4 所示。

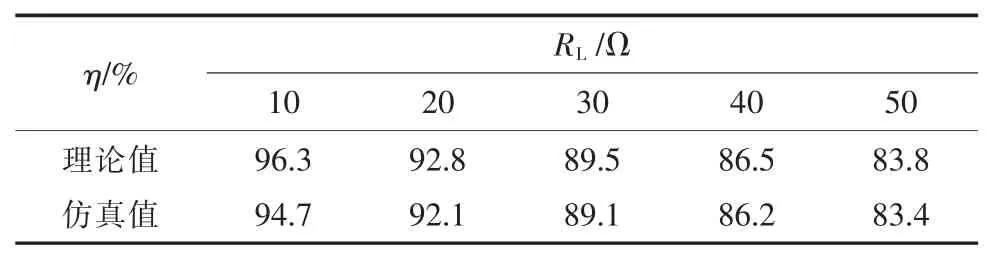
表2 负载变化时效率的理论值与仿真值

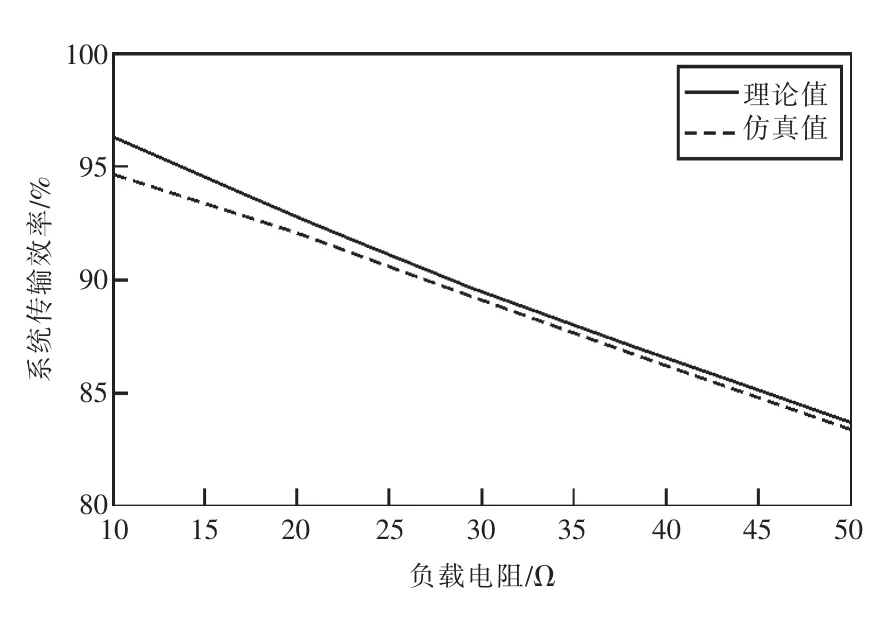
图4 负载变化时效率的理论值和仿真值曲线

由图4 可知，负载变化时，传输效率的理论值和仿真值具有很好的一致性，尤其是在负载电阻相对较大时，仿真结果验证了理论分析的正确性。另外，从图4 中还可以明显看出负载对效率的影响关系，即负载电阻越大，系统效率越低。

2.2 传输距离对效率的影响

由式（16）知，随着传输距离的增大，由于耦合系数减小，系统的传输效率也降低。尤其在传输距离为半径的2 倍之后，距离的变化会对效率产生较大的影响。现对传输距离变化时的系统进行仿真，分析其传输效率，验证理论分析的正确性。

假设其他因素不变，改变系统传输距离，仿真时即是改变线圈间的互感M。负载RL取10 Ω，传输距离d 变化时，系统传输效率η 的理论值和仿真值结果如表3 所示，转换成效率曲线如图5所示。

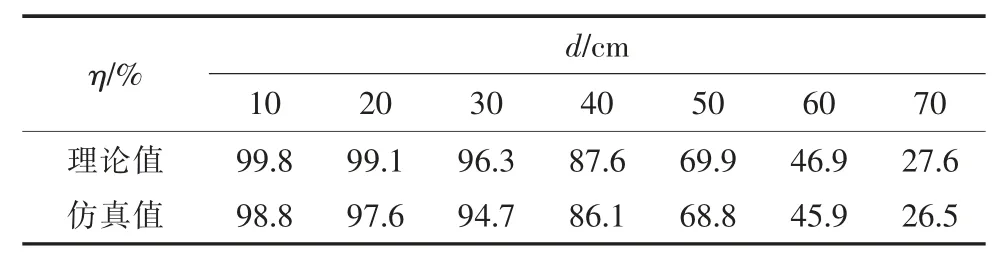
表3 传输距离变化时效率的理论值与仿真值

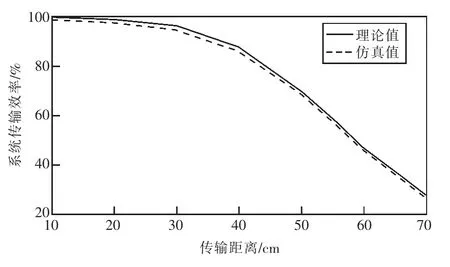
图5 传输距离变化时效率的理论值与仿真值曲线

由图5 可知，传输距离变化时系统传输效率的理论值和仿真值具有很好的一致性，尤其是在传输距离较大时，仿真结果验证了理论分析的正确性。另外，由图5 还可以明显地看出传输距离对系统传输效率的影响关系，即传输距离越大，系统的传输效率越低，特别是在传输距离大于2倍线圈半径时，系统传输效率下降尤其明显。

2.3 系统频率对效率的影响

系统频率对效率的影响分为系统电源频率与系统自然谐振频率相同和不同2 种情况。

2.3.1 电源频率与系统自然谐振频率相同

取线圈半径r=20 cm，线径a=1.4 mm，线圈匝数N=4。通过改变外加电容的值改变系统自然共振频率。传输距离取40 cm，负载RL取30 Ω，电源电压峰值为100 V，电源频率同系统自然谐振频率。不同外加电容时谐振频率值见表4。

表4 不同外加电容时谐振频率

谐振频率变化时效率的理论值与仿真值如表5 所示，转换成效率曲线如图6 所示。

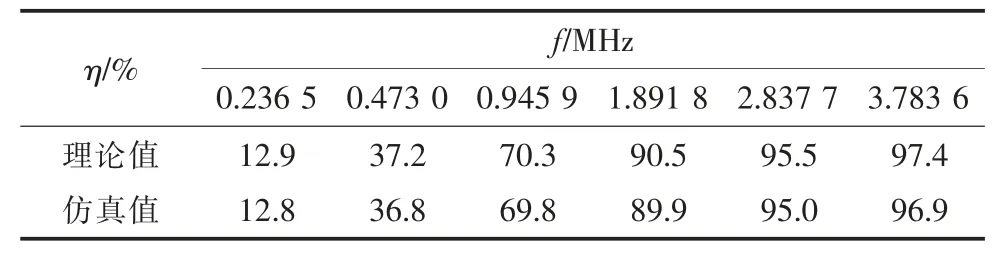
表5 谐振频率变化时效率的理论值和仿真值

由图6 可知，传输距离变化时系统传输效率的理论值和仿真值具有非常好的一致性，仿真结果验证了理论分析的正确性。另外，从图6 中还可以明显地看出系统频率对系统传输效率的影响关系，即系统频率越大，系统的传输效率越高。

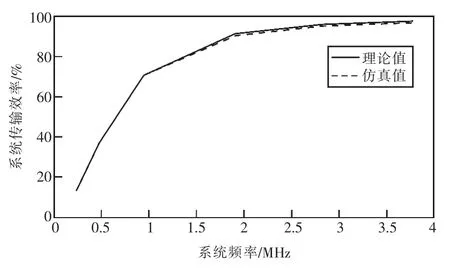
图6 谐振频率变化时效率的理论值和仿真值曲线

2.3.2 电源频率与系统自然谐振频率不同

取线圈半径r=20 cm，线径a=1.4 mm，线圈匝数N=4。外加电容的值取1 nF，系统的自然谐振频率固定为0.945 9 MHz。传输距离取40 cm，负载RL取30 Ω，电源电压峰值取100 V。

仿真时改变系统电源频率，经过仿真与计算，得到不同电源频率时传输效率的仿真值如表6 所示，转换成效率曲线如图7 所示。

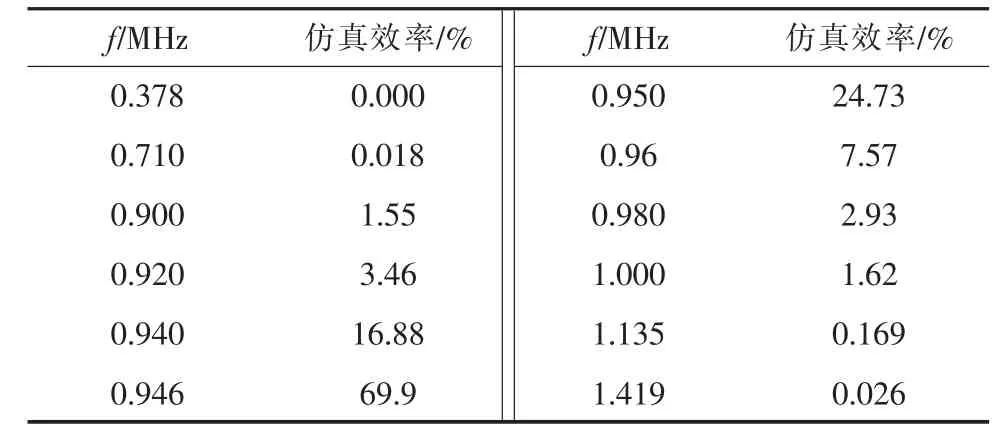
表6 系统电源频率变化时效率的仿真值

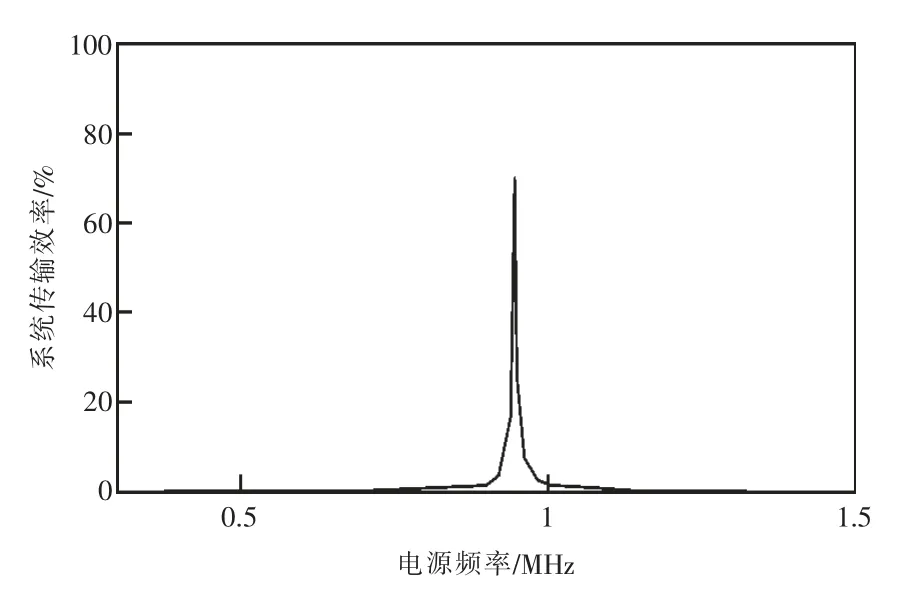
图7 电源频率变化时系统传输效率仿真值曲线

由图7 可知，电源频率变化时，传输效率变化十分明显。图7 中效率极大值点是电源频率与系统自然谐振频率相等时取得。当电源频率与系统自然谐振频率不等时，两者之差有些微小变化，传输效率就急剧下降。所以，系统运行过程中保持电源频率与谐振频率相等是十分必要的。

2.4 线圈尺寸对效率的影响

线圈尺寸参数包括线圈形状、线圈半径、线圈匝数、线圈材料、线径以及线圈实现方式（单股、多股并联）等。线圈形状影响了磁场的分布情况及电感，线圈材料以及线圈实现方式会影响线圈等效阻抗（线圈的电路品质因数）。前文1.4 小节的理论分析均是基于单股多匝圆形线圈模型，所以仿真中只讨论线径、线圈半径以及线圈匝数对系统传输效率的影响。

2.4.1 线圈匝数、半径及线径对线圈参数的影响

保持频率为0.945 9 MHz 不变，线圈半径r=20 cm，线径a=1.4 mm，改变线圈匝数N。改变线圈匝数会改变线圈电感，因此要进行电容匹配。传输距离取40 cm，线圈匝数变化时各相关参数变化情况如表7 所示。

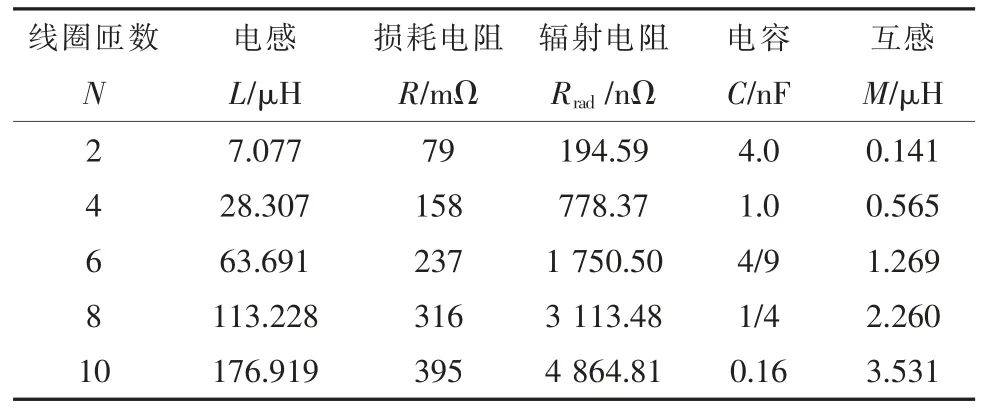
表7 线圈匝数变化时各相关参数值

保持频率为0.945 9 MHz 不变，线圈线径a=1.4 mm，线圈匝数N=4，改变线圈半径r。改变线圈半径会改变线圈电感，因此要进行电容匹配。传输距离取40 cm，线圈半径变化时各相关参数变化情况如表8 所示。

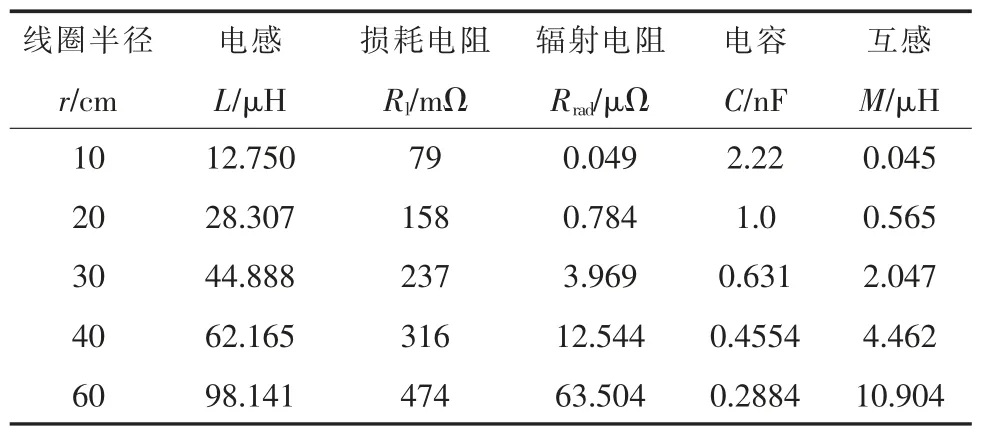
表8 线圈半径变化时各相关参数值

当保持频率为0.945 9 MHz 不变时，取线圈半径r=20 cm，线圈匝数N=4，改变线圈线径a。改变线圈线径会改变线圈损耗电阻，因此要进行电容匹配。传输距离取40 cm，线圈匝数变化时各相关参数变化情况如表9 所示。

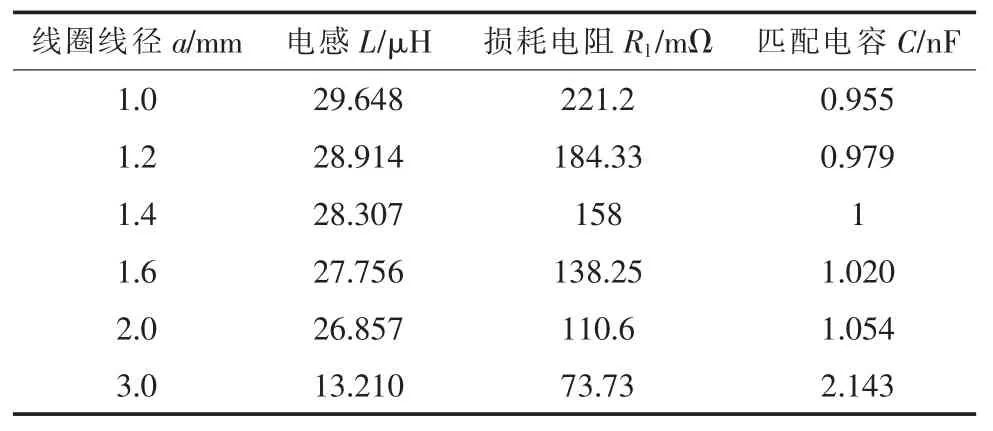
表9 线圈匝数变化时各相关参数值

2.4.2 线圈参数对效率的影响

负载RL取30 Ω，电源电压峰值为100 V。通过仿真与计算，线圈匝数N 变化时效率的理论值与仿真值如表10 所示，线圈半径r 变化时系统的传输效率的理论值与仿真值如表11 所示，线圈线径a 变化时效率的理论值与仿真值如表12 所示。

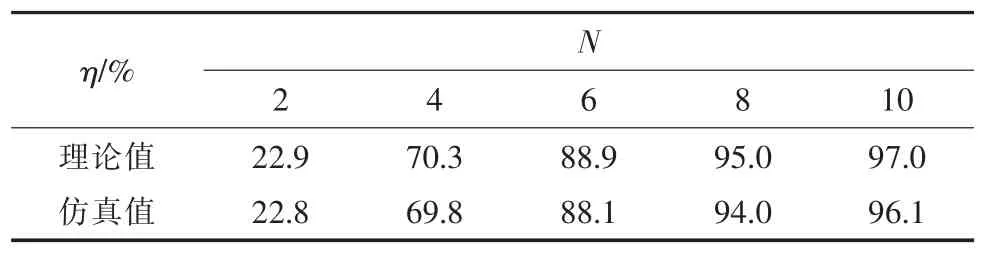
表10 线圈匝数变化时效率的理论值与仿真值

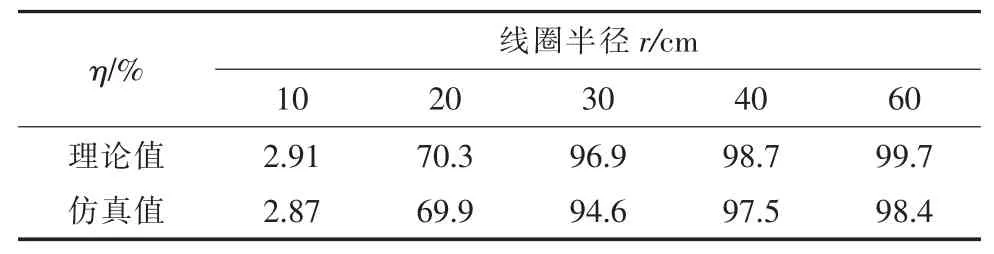
表11 线圈半径变化时效率的理论值与仿真值

由表10—表12 可知，线圈匝数变化时，系统传输效率的理论值和仿真值具有非常好的一致性，仿真结果验证了理论分析的正确性。另外，从表10还可以明显地看出线圈匝数对系统传输效率的影响关系，即线圈匝数越多，线圈半径越大，线圈线径越大，系统的传输效率越高。因此，改变线圈参数可以明显提高传输效率。

3 结语

本文详细分析了磁耦合谐振式无线电能传输技术的机理，对其模型进行了分析，并建立系统等效模型，得到系统传输效率公式，从而得出了影响系统传输效率的因素，包括：负载阻抗、系统频率、线圈线径、线圈半径、线圈匝数、线圈位置和传输距离。根据理论分析得到影响效率的各个因素，通过MATLAB/Simulink 逐一仿真验证了这些因素对效率的影响效果，为后续研制远距离、大功率及高效率的无线电能传输系统提供理论依据和发展方向。