编组站阶段计划与动态车流的耦合及调整研究
2020-03-20范千里
薛 锋,赵 蕾,范千里
(1.西南交通大学,交通运输与物流学院,四川 成都 611756;2.西南交通大学 综合交通大数据应用技术国家工程实验室,四川 成都 611756;3.西南交通大学 综合交通运输智能化国家地方联合工程实验室,四川 成都 611756;4.中国建筑西南设计研究院有限公司 市政设计院,四川 成都 610041)
编组站作业计划包括日班计划、阶段计划以及调车作业计划,其中阶段计划较为精细,起着承上启下的关键作用。以按时发车为目标,研究编组站阶段作业计划与动态车流之间的耦合关系,并在此基础上计算其耦合度,用以度量阶段计划编制时不确切的时间估计对调度的影响程度,能够为阶段计划的实时调整提供依据。
目前,国内外对编组站阶段计划的研究较多。牛惠民等[1]将车辆在站走行距离和集结时间、交换时间等作为目标函数,构造车流接续综合优化模型,并使用遗传算法求解;何世伟等[2]运用模糊集合论及系统优化的方法,模糊化定义了编组站阶段计划中的柔性概念,建立了编组站阶段计划刚性与柔性优化综合协调问题的模糊混合0-1规划模型;王慈光[3]将编组站配流问题转化为运输问题,建立了静态配流问题的网络模型并求解;景云等[4]、王琦[5]等对不确定条件下的编组站作业计划进行了优化研究;黎浩东[6]对鲁棒阶段计划编制及调整问题进行了研究;赵军[7]采用进路模式表示决策任务,将调度任务问题转换为运输指派问题,并在此基础上设计了新的模型;马亮[8]在编组站静态阶段计划优化的基础上,建立了编组站阶段鲁棒性动态调整模型。国外在研究编组站作业优化问题时,通常针对所研究的具体问题进行建模,最后转化为数学问题进行求解,很少对阶段计划系统性的微观问题进行分析[9-12]。国内外对编组站阶段计划的研究重点在配流、调机与到发线运用等问题的优化方面,对于编组站阶段计划与动态车流之间的关系及其协调程度的度量研究较少,根据现有研究很难给出阶段计划与动态车流之间耦合程度的度量值,只能根据部分参数给出一个区间范围。
明确编组站阶段计划与动态车流之间的协调程度,有利于编组站调度人员充分掌握计划的执行情况,以便对阶段计划进行调整。本文对编组站到达列车信息及解编作业时间容许波动范围进行界定,考虑当车站出现大幅度车流波动时,以车站发车总权值最大为目标,建立自编始发列车车流来源调整模型。通过对出发列车的车流来源进行适当调整,减小车流波动对车站运营的影响;通过对编组站阶段计划与动态车流的耦合度进行研究,验证调整结果对列车出发情况的影响程度,使阶段计划与动态车流耦合程度的评价更具合理性与可靠性。
1 到达列车信息及解编作业时间容许波动范围
1.1 到达列车容许晚点时间
编组站资源按照既定的作业计划在不同时段被相应的作业序列所占用,当列车的某项作业出现延误,不能按照既定计划实施时,需要该作业占用资源执行其他作业时,可以利用其他作业间的间隙执行该作业,作业资源占用示意见图1。

图1 作业资源占用示意


(1)
(2)
式中:ti为作业i的预计用时,min。
在到达列车的解体作业计划及负责其解体的调机、驼峰等资源安排已确定的情况下,当有列车出现晚点,其作业由于计划的执行限制需要使用原定计划安排的调车设备时,为了不对其他列车的作业产生干扰,其作业时间不能与其他列车的作业时间产生冲突,其前后作业关系见图2。

(3)

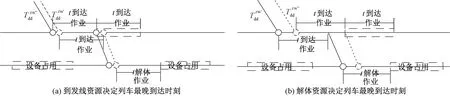
图2 列车最晚到达时刻示意图

(4)

由图2可知,列车最晚到达时刻为
(5)
1.2 解体作业时间容许范围
1.2.1 到达列车最早开始解体时刻
按照原定列车到达计划,当不存在资源冲突时,到达列车在进行完列检作业后可以立即开始解体作业;当存在资源占用冲突时,需待之前占用资源的作业执行完毕,且存在的剩余时间窗大于预估解体时间时,才可以开始进行解体作业。当存在的剩余时间窗小于预估解体时间时,到达列车的最早开始解体时刻需向后推移,直至出现大于预估解体所用时间的空闲时间窗为止。对上阶段到达的列车,最早开始解体时刻
(6)

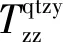
1.2.2 到达列车最晚解体结束时刻
根据车站阶段计划可知每列到达列车中的车流预计去向,当与之接续的列车中最早编组的一列列车开始编组前,该到达列车必须解体完毕,否则就无法实现预定车流的接续过程,于是有列车最晚解体结束时刻
(7)

1.3 编组作业时间容许范围
1.3.1 出发列车最早开始编组时刻
当阶段计划中出发列车所需车流解体或取送车作业毕后,就可以开始编组。在进行出发列车最早编组时间的推算时,也要考虑出发列车编组作业与其占用相同设备、设施资源的其他作业在时空上的冲突。出发列车最早开始编组时刻为
(8)

1.3.2 出发列车最晚编组完成时刻
列车的编组作业需最晚于列车出发时刻限制约束之前完成,与上述时间推算一样,也需考虑与其他作业的冲突情况,出发列车最晚编组完成时刻
(9)

取送车等作业的时间限制由解体最早开始时刻、编组最晚结束时刻和其他占用作业资源的作业时间、空间关系决定。
2 编组站阶段计划与动态车流耦合度计算
编组站系统存在前后的耦合作业关系,按照车流输入与输出的方向主要为到解系统与编发系统,见图3。
编组站阶段计划在编制时,站调需考虑各项作业的执行时间、作业地点、作业对象和作业执行者这四个要素,其中作业时间及作业对象存在不确定性。阶段计划的编制目标需要考虑将编组站的车流波动控制在合理范围内,并通过计划控制站内车流的流动及输出。阶段计划的执行需要车流来保障,当车流方向、数量不能满足车站相关约束要求时,阶段计划就无法正常实施。这种阶段计划与动态车流间的不吻合现象,会对车站调度产生不利影响,为此需要考虑二者之间的耦合情况,以评估车流的波动对调度作业的影响。

图3 到解系统与编发系统示意图
每个系统的协调情况由若干指标组成,为s1,s2,s3,…,sn。到解系统中相关指标包括:晚点到达列车数、列车解体未完成数、实际车流内容与预计车流不吻合的列车数,这些为负向指标;按计划时段完成解体的列车数,为正向指标。编发系统的相关指标包括:按原定计划发出的列车数,为正向指标;在规定时段内编组未完成列车数、未正点发车列车数,为负向指标。以1 h为单位,进行累加统计,系统α指标β的功效为
(10)
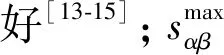
编组站单个系统的总功效计算公式为
(11)
式中:wαβ为各指标所占权重。
wαβ计算步骤如下:
Step1根据系统α指标β的不同重要程度,设置[1,3,7,9]的重要度指标,将指标β与其他指标q对比,同等重要时取值dqβ为5,其他指标明显重要时dqβ取1,其他指标较为重要时dqβ取3,指标β较为重要时取dqβ为7,指标β明显重要时取dqβ为9。
Step2β=β+1,转Step1,设存在v个指标,当β=v时,转Step3。
Step3取max{dβ},min{dβ},β=1,2,3,…,v,记为maxβ与minβ,计算向量Dβ=(d1β,d2β,…,dvβ)与maxβ、minβ间欧氏距离d(maxβ,Dβ)与d(minβ,Dβ)。
Step4记rβ=d(minβ,Dβ)/[d(maxβ,Dβ)+d(minβ,Dβ)]。

若编组站由h个系统组成,则编组站阶段计划与动态车流间耦合度C为
(12)
阶段计划与动态车流间的耦合度界定为实际到达车流内容波动对车站调度影响程度的量化。当实际车流波动较大时,若仍按照原定的列车车流来源计划执行编组作业,将对车站原定的列车出发计划产生较大影响,同时导致阶段计划与动态车流间的耦合度过低。
3 受影响出发列车的编组调整
当列车到达时刻晚于最晚到达时刻时,原定与该到达列车车流衔接的出发列车定然会受到影响,调度人员需要通过合理调控将这种不利因素造成的影响控制在最小的范围内。受影响出发列车的计算方法如下:
在列车i到达晚于容许最晚到达时刻的情况下,列车i中的车流已经不能用于本阶段原与之匹配的接续车列中。cfj表示由于列车i的晚点将可能受到影响的第一列自编始发列车,其在该阶段计划中为第j列出发的列车。K表示该车站全部的车流组号,{k′,k,…,k″}∈K为列车cfj中所包含的车流组号的集合。
当存在
(13)

当存在
(14)

(15)
当存在Gj≥mj对于j∈{1,2,3,…}均成立时,所有列车的编组和出发作业都有可能实施。反之,肯定会有一列或几列自编列车的编组和出发受到影响。
综上所述,当出现列车晚于最晚容许到达时刻的情况时,可以得到其接续列车及其后续列车能否正常编组的判断方法。

图4 出发列车车流来源示意图
从图4可知,如果随列车dd2中到达的方向为A、a的车流不足以满足列车cf2的满轴约束时,列车cf2与cf1间存在车流竞争。根据车站原定解编计划,当出现大范围列车晚点或实际车流信息与预定车流信息不符时,会出现严重的车流不足情况,各列车间的车流竞争激烈,需要对自编始发列车的车流来源进行调整。在不改变自编始发列车出发顺序的情况下,若减少部分低等级列车的车流供应量,释放其中的一些车流,以优先满足与之具备车流竞争关系的高等级列车的车流需求,则可能会使得到达列车晚点或到达车流信息不匹配等情况对车站作业计划的影响程度相对降低。

在出现列车晚于最晚到达时刻时,其中所需车流出现接续中断,本阶段计划无法按照原定计划发出,考虑车站的整体作业,为了使得阶段计划自编始发列车兑现率最高,根据直达高于直通、直通高于区段、区段高于摘挂、摘挂高于小运转的顺序对出发列车划分等级[16],赋予不同权重,根据出发列车的等级排序优先满足高等级列车的车流需求。在相同等级情况下,优先满足先出发列车的车流需求,以出发列车的权重之和最大为目标,建立车流变动时调整列车编组内容的优化模型。
设变量
(16)


以发出列车权重之和最大为目标,建立出发列车的车流来源调整模型为
FMAX=θj×εj
(17)
syc0-θ1×Xcf1≥0
∀j∈{1,m-1},sycj=sycj-1-θj×Xcfj-1
∀j∈{1,m-1},sycj+zjcj+1-θj+1×Xcfj+1≥0
sycj+zjcj+1≤rcs
(18)
(19)
(20)
(21)
(22)
(23)

式(18)为列车编组时各组号车流的数量判断约束;式(19)~式(21)为自编始发列车占用车流与到解列车释放车流之间的约束关系;式(22)表示车辆接续的时间约束条件;式(23)表示自编始发列车的轴重约束。
根据上述思路对出发列车车流来源进行适当调整,以最大限度保障原定列车出发计划的执行。列车的调整步骤如下:
Step1统计出现过度晚点列车时车站各车组车流情况,按照车流组号顺序表示为行向量K。

Step3j=j+1。
Step4最大出发列车序号为n,当j=n时,转Step5,否则,转Step2。

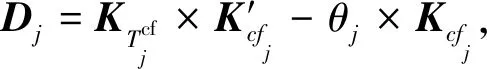
同理,sycj-fccj+zjcj+1-θj+1×Kcfj+1≥0处理如下:


表1 到达列车实际情况与预计情况差异
Step6上述问题属于整数线性优化问题,首先使用MATLAB整数优化工具箱确定出发列车的编组序列,再利用遗传算法,以minF=-θj×εj为适应度,对自编始发列车的车流来源问题进行求解,通过上述步骤,确定出发列车序列和出发列车的编组内容及车流来源。
4 算例分析
以文献[8]中的数据为基础进行分析验证。根据列车到达计划、解体计划和编组计划等可以推算出列车到达时间容许波动范围和各项作业时间容许波动范围,绘制列车到达时间、作业时间容许波动范围见图5、图6。

图5 列车到达时间与解体作业时间容许波动情况

图6 编组作业时间容许波动情况
假定列车实际到达情况与原计划差异情况见表1。
列车到达时间或作业时间超出容许波动范围,或者列车、车辆信息变动超出容许范围时,该列车中的车流已无法与原定计划中的出发列车形成车流接续,此时如果车站剩余车流可以满足计划出发列车的车流需求,则通过车流来源调整,不会对出发列车产生影响;如果车站存车无法满足出发列车车流需求,则部分出发列车必定会受到影响。用与第2节计算wαβ相同的方法确定出发列车权重取值见表2,在此基础上,根据列车权重确定列车车流获取优先度,对优先度高的列车优先分配车流,按照式(17)~式(23)所示的模型对车流进行重新分配,以泊松分布为基础对出发列车时刻波动情况进行模拟,可得调整前后的列车出发情况见表3。
在对既定列车车流来源进行优化调整的基础上,根据车站列车编组方案,新增部分自编始发列车,以后续到达车流对车站的冲击最小为目标,确定调整后新增的出发列车见表4。
调整后,各自编始发列车的车流来源情况见表5。
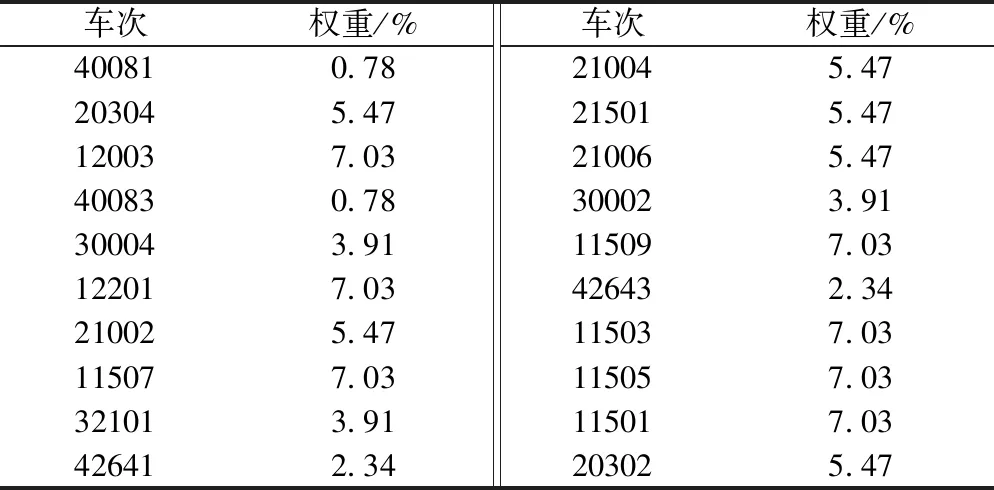
表2 出发列车权重取值表
由表3~表5可知,调整前列车11509次编组内容32128/C/16,47667/C/21,32116/C/18,32118/C/2,由于列车32128次的车流组号为C的车流不足,导致列车11509次的编组受到一定影响,当调整列车11509次的编组内容为32128/C/12,47667/C/21,32116/C/18,32118/C/6后,得以满足编组条件;调整前列车40083次的编组内容为ZCCL/21/23,ZCCL/29/39,与列车32101次存在车流竞争关系,由于组号为029的车流不足,将导致32101次列车无法满足轴重约束,调整后取消列车40083次的编组,使得较高等级的列车32101次中所需车流得到满足。
根据上述数据统计列车到解系统和编发系统各指标值见表6、表7。

表3 调整前后的出发列车表
注:其中A/B,A表示调整前数据,B表示调整后数据。

表4 调整后的新增出发列车

表 5 自编始发列车车流来源表
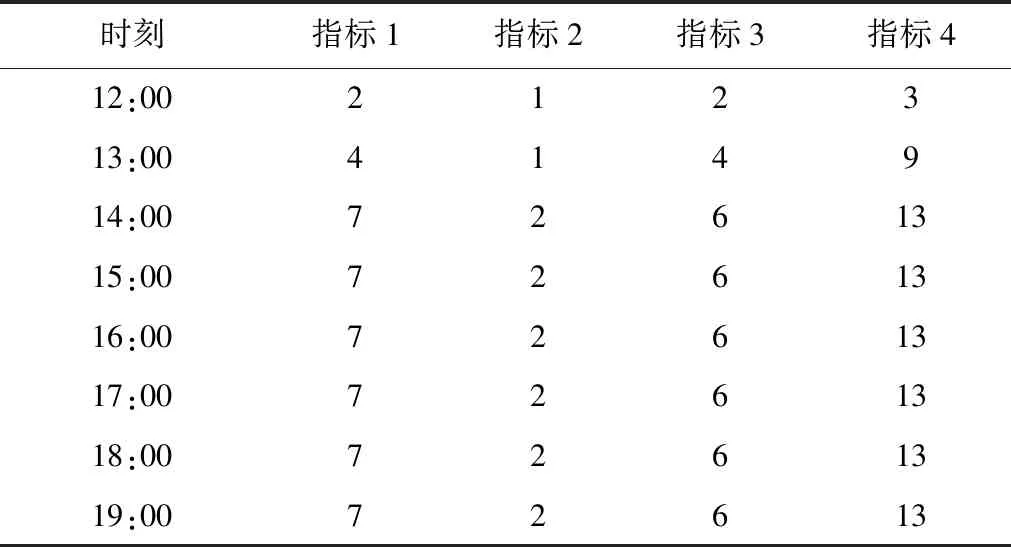
表6 到解系统指标取值
其中指标1表示晚点到达列车数,指标2表示列车解体未完成数,指标3表示实际车流内容与预计车流不吻合的列车数,指标4表示按计划时段完成解体的列车数。

表7 调整前后编发系统指标取值
其中指标1表示编发系统发出的列车数,指标2为在规定时段内编组未完成列车数,指标3为正点发车列车数,指标4为发出车辆数。
对表6和表7中的数据进行标准化处理,根据第2节的方法,到解系统4个指标权重确定为w11=0.2、w12=0.3、w13=0.2、w14=0.3,编发系统3个指标权重确定为w21=0.1、w22=0.3、w23=0.2、w23=0.4。按照式(12)计算编组站阶段计划与动态车流之间耦合度情况见表8。

表8 系统耦合度
绘制系统耦合度情况见图7。

图7 阶段计划与动态车流耦合度变化情况
根据耦合度计算公式可知,当耦合度C∈(0,0.4]说明系统耦合度很弱,当C∈(0.4,0.5]说明耦合度弱,当C∈(0.5,0.7]说明耦合强度中等,当C∈(0.7,0.85]说明系统耦合强度较高,当C>0.85时,说明系统耦合强度极高。从表8可知,算例计算所示调整前后编组站作业计划与动态车流耦合关系一般,在开始时系统耦合强度为0.458,随着晚点列车的增多及车流内容的波动,耦合强度逐渐减小,调整后17:00之后的耦合度均值较调整前17:00之后的耦合度均值高0.029。图7为调整前后作业计划与动态车流耦合度图示,从图中可以看出调整后耦合强度先逐步减小,后来出现较大幅度的上升。
5 结论
本文通过耦合度,研究编组站阶段计划与动态车流之间的关系,并进行适当调整。考虑车站阶段计划既定情况下,当出现列车到达时间或车辆信息波动较大时,在不改变原有列车编组顺序的基础上,适当调整计划内车流来源,以使阶段计划受到的影响最小。选取到解系统与编发系统相应指标,计算调整前后编组站阶段计划与动态车流的耦合度,并用算例进行了验证,得到以下结论:
(1)车站的解编作业计划易受到车流波动的影响,到达列车车流内容、解编作业时间等的变动都会对阶段计划与动态车流的耦合度产生较大的影响。当列车晚点、车流状态等信息波动超出范围时,根据现车情况和出发列车不同等级,以车站阶段发车总权值最大为目标建立模型,可实现待编列车车流的重新调配。
(2)算例计算中,优化调整之前受影响出发列车为10列,调整之后为6列,且调整后阶段计划与动态车流之间的耦合度在17:00之后区段的均值较调整前该区段的均值增加了6.819%,这说明进行适当的车流来源调整可以在一定程度上减少实际车流内容的波动对车站作业的影响。
(3)通过计算编组站阶段计划与动态车流间的耦合度,能够细致分析编组站阶段计划的执行情况,可以为车站的实时调度调整提供依据。
