基于时空网络的城际高速铁路列车开行方案优化方法
2020-03-20谭宇超申纯燕
秦 进,谭宇超,张 威,申纯燕,赵 成
(1.中南大学 交通运输工程学院,湖南 长沙 410075;2.中南大学 轨道交通安全教育部重点实验室,湖南 长沙 410075;3.广深铁路股份有限公司 深圳北车站,广东 深圳 518010)
城际高速铁路是在人口稠密的都市圈或城市群中修建的高速铁路客运专线,其主要特点是线路距离较短、列车班次公交化,且列车最大运行速度一般不低于250 km/h,兼有城际铁路和高速铁路的特征,目前京津、沪宁、武汉、长株潭等主要城市群的城际铁路已在区域经济发展中发挥重要作用。但是要高效运用城际铁路的设施与服务,必须建立起科学的组织理论与方法。列车开行方案是连接客流需求和列车时刻表的桥梁,一般包括列车等级、开行区段、停站方案、列车编组和开行频率等内容。作为组织和利用城际铁路能力的关键环节和技术,列车开行方案的编制质量直接关系到高速铁路的市场竞争力和服务质量水平。
列车开行方案问题在国内外已经得到了广泛关注和深入研究。文献[1]将包含不同类型列车的开行方案问题描述为多商品流网络问题进行分析。文献[2]以旅客旅行时间最短和换乘惩罚成本最小为目标,建立0-1整数规划模型。文献[3]假设同OD对的旅客会选择相同最短路径出行,并以列车运行成本和旅客旅行时间最小为目标建立了多商品流模型。文献[4]针对城市轨道交通跨站越行模式,建立了双目标非线性混合整数规划模型。文献[5-8]利用多目标优化模型、双层规划模型、弹性需求等方法,对列车开行方案相关问题进行了深入研究。文献[9]提出了高速铁路列车停站的两阶段优化方法。文献[10]构建了不确定需求下高速铁路列车停站方案的机会约束规划模型。为了满足高铁旅客的时变性需求,很多研究也建立了基于时刻表的离散整数规划模型。文献[11]针对以旅客选择为基础的高速列车时刻表铺画问题,建立了离散事件仿真模型和约束Logit选择模型。文献[12]不考虑列车能力限制,从列车成本和旅客成本两方面出发,对列车开行方案和列车运行时刻进行综合优化。文献[13]在列车开行方案优化过程中考虑了列车运行图优化,以铁路利益最大化为目标建立优化模型,但暂时还不能适应大规模实际问题。文献[14]建立了基于列车候选集的高速铁路列车开行方案优化方法,但其中列车区段和停站方案来源于现有开行方案,当客流特征发生改变时,其适用性会有所降低。
时空网络方法在处理带时间维度的问题时具有易建模、求解便利等优势,国内外很多学者在研究公共交通问题时都会使用时空网络方法。文献[15]使用时空网络来研究航班机型分配问题。文献[16]建立了基于离散时空网络的不正常航班调度模型。文献[17]根据旅客列车运行图构造了列车时空服务网络,在此基础上提出了体现旅客时空差异服务需求约束的客流分配模型及算法。文献[18]考虑线路中断后的情况,在时空网络上建立了以旅客负效用和企业成本最低为目标的0-1整数规划方法。
综上所述,目前关于列车开行方案的研究主要集中在停站方案、开行频率等单个方面的优化研究,综合考虑这些因素的研究较少,时空网络方法也多应用在列车时刻表优化问题和列车开行方案基础上的客流分配问题。本文从实际出发,在给定的运输线路和客流需求条件下,构建城际铁路运营时空网络,在此基础上考虑设备资源限制、时空网络客流及列车流守恒、客流需求特征和城际列车时空运行规律等,建立基于时空网络的列车开行方案优化模型,并利用双层模拟退火算法进行求解和计算分析。
1 问题分析
在城际铁路线路列车开行方案中,每列列车可以用一组途经车站的有序序列来表示,表示列车的运行起讫点和停站方案,并且有途经各个车站的到达和离开时刻,通过列车的发车时刻可以推算出列车的开行频率。
在城际铁路列车提供具有高速度、高密度特征运输服务模式下,城际客流需求具有明显的时变特性,即城际出行需求在运营时间段内,每对起讫站之间的需求大小都会随着时间的变化而变化。以沪宁城际高速铁路为例,如图1所示,根据城际铁路售票数据,2017年5月31日的沪宁城际下行方向客流需求,呈现出明显的小时变化特征,上午高峰期客流与晚间客流差异极大。
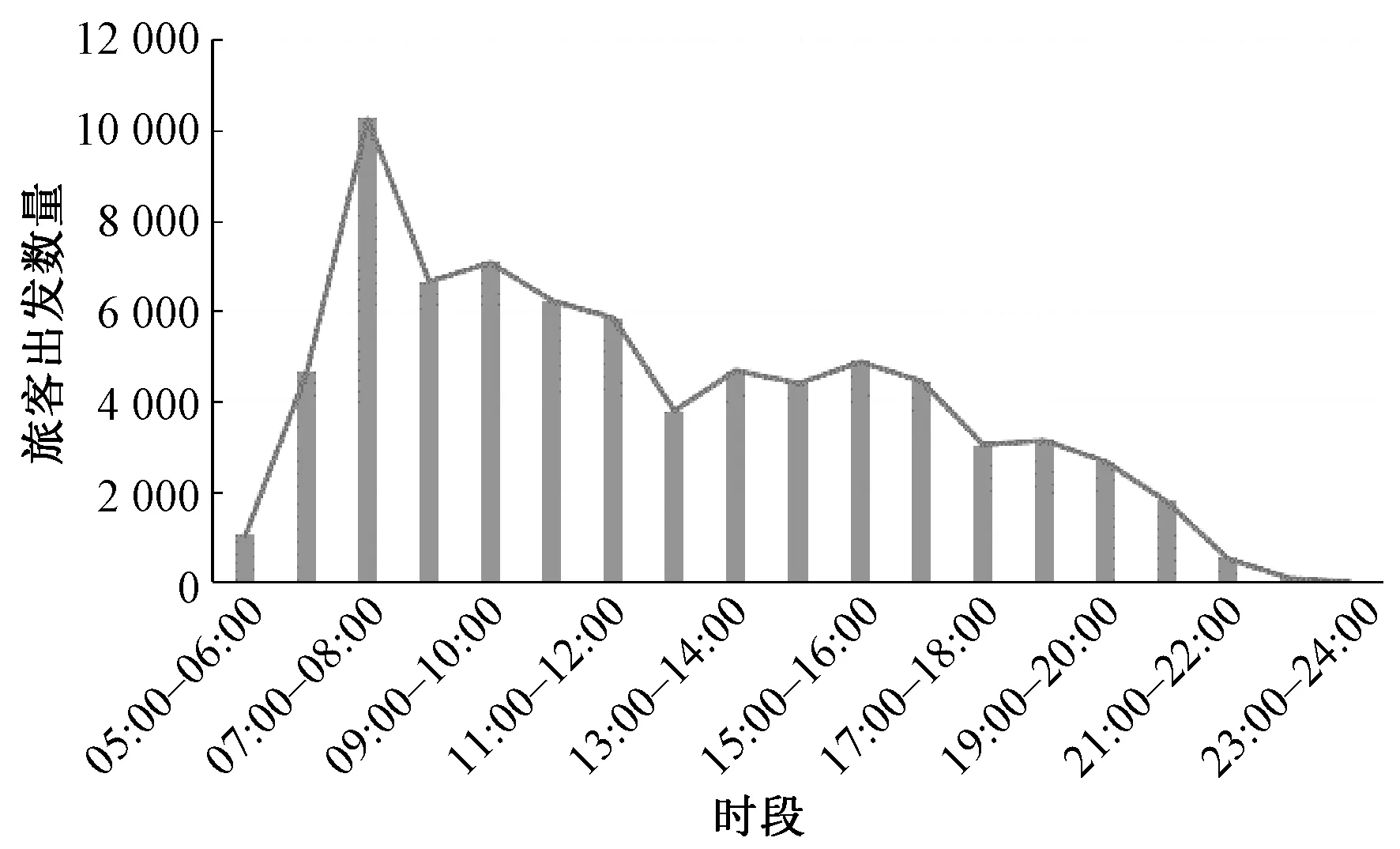
图1 2017年5月31日沪宁城际下行方向每小时旅客出发数量
尽管城际铁路客流需求实际是一个随时间变化的函数,但是在一定的时间段内,客流需求仍是可以被视为一个固定不变的常量,因此可以考虑将城际铁路总的运营时段划分为若干个小的时间段,假设每个时间段内的客流需求都固定不变,由此可将时变需求转化为固定客流需求,从而有效简化问题分析。
城际铁路旅客出行时,若列车发车时刻与期望出发时刻存在差异,将会为旅客带来不便。如果能在开行方案决策过程中,适当考虑旅客期望出发时刻信息,必然可以保证决策者能更全面的从空间和时间两个角度进行方案评价,以保证所得方案的整体最优。
时间信息的加入无疑会显著增加问题的复杂度。结合问题的特性,可以考虑引入能将时间和空间要素进行有机结合的时空网络方法进行问题的分析和优化。列车开行方案的时空网络模型会增加列车在沿途各站到发时刻的信息,可在方案优化的同时处理时变客流分配问题,从而为考虑时间信息的城际列车开行方案优化问题的建模和求解带来极大便利。尤其是该方法可根据实际情况灵活调整时间信息的精确度。
为简化问题,做如下合理假设:
(1)列车运行时间只考虑区间纯运行时分,不考虑起停附加时分。
(2)列车采用固定编组,所有列车等级相同。
(3)城际列车间隔时间类型众多,为提高计算效率,同时获取合理的列车运行时间估计值,仅考虑始发车站的发车间隔时间,因此会有部分列车运行线发生冲突的可能。
(4)假设线路上下行列车是对称开行,即上下行列车开行方案一致,暂不考虑动车组运用问题。
2 模型构建
2.1 列车开行方案的时空网络构造
图2为某城际高速铁路线路,其上的车站集合为S,车站数量为|S|。图中节点代表车站,弧代表车站之间的线路。

图2 城际高速铁路线路示意图




图3 城际列车开行方案时空网络示意图
2.2 模型变量
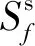

2.3 优化模型
基于所构建的列车开行方案时空网络,可构建城际列车开行方案的0-1规划模型。模型的优化目标是最小化系统内的列车运行成本和旅客出行成本,同时考虑时空网络中的时空节点上列车流和客流守恒特性,列车流和客流之间的时间逻辑,以及铁路行车组织要求的车站发车间隔时间、列车定员、列车运行总数等约束条件。
列车运行成本由列车在弧段上运行时间表示,旅客出行成本由旅客在弧段上出行时间、出发偏差时间和未登上列车旅客惩罚时间表示,这4者的线性组合构成模型的优化目标函数。

(1)

(2)
(3)

则旅客出发偏差总时间Ψ3为
(4)

(5)
对于列车运行时间Ψ1、旅客弧段出行时间Ψ2、旅客出发偏差时间Ψ3和未登上列车旅客惩罚时间Ψ4,引入加权参数δ1、δ2、δ3、δ4,组合生成列车开行方案优化目标为
minZ=δ1Ψ1+δ2Ψ2+δ3Ψ3+δ4Ψ4
(6)
优化模型中需考虑的约束如下:
①列车流守恒约束
(7)
(8)
式(7)为在时空点上的列车流守恒约束,使得到达时空点(j,τ)的列车数减去终到列车数等于离开时空点(j,τ)的列车数减去始发列车数;式(8)保证列车流在其中间途经时空点守恒。
②客流守恒约束
(9)

(10)
(11)
③决策变量关系约束
(12)
时空网络中旅客只能使用有列车经过的弧段,即在任意弧段上,任何旅客群体的决策变量值均不能大于任何列车决策变量值。
④列车定员约束
(13)
式(13)表示同时乘坐同一列车的旅客数应不大于列车定员数。
⑤始发车站发车时间间隔约束
(14)
∀t′≤t+ε∀f≠f′
f,f′∈Ωi∈Sf∩Sf′j′∈Sf′
式(14)表示始发车站任意两列列车的发车时间间隔不小于固定值ε。
⑥列车总数约束
(15)
这主要是考虑列车数量对企业的运输效率与能力有重要的影响,开行过多的列车必然会增加成本,同时使线路区间与车站能力接近饱和,因此应对列车使用数量进行限制,即列车开行方案Ω使用的列车数不大于给定值b。
⑦变量取值约束
(16)
(17)
(18)
根据以上分析,就可建立基于时空网络的城际高铁列车开行方案优化模型为
3 求解算法
基于时空网络的高速铁路列车开行方案优化模型,实际上是一个大规模的0-1整数规划模型,其计算复杂度随着列车和车站的数量增加而呈现几何级增长,目前的精确算法很难在有效时间内获得问题的满意解。本文使用基于模拟退火算法(Simulated Annealing,SA)设计模型的求解方法。

图4 内层算法邻域解
基于时空网络的高速铁路列车开行方案优化模型,需要同时优化列车的运行起讫点、停站方案、服务频率及列车在停站到发时刻4项内容,由于区间运行时分均为定值,因此结合列车始发时刻与停站方案,就能获得列车沿途各站的到发时间,结合列车始发时刻与区段列车数量,就能获得列车服务频率,由此可将模型优化内容简化为列车运行起讫点、停站方案、各运行区段开行数量及始发时刻4项内容。考虑到停站方案是在运行起讫点和开行数量确定的基础上才能优化确定,因此所建立模型可以分为上下两层进行决策。根据这一特点,设计了双层SA算法进行城际高速铁路列车开行方案优化模型求解,即将问题分为内外两层进行求解,其中外层SA算法首先确定列车运行起讫点、开行数量和始发站始发时间,在外层决策的基础之上,内层SA算法优化列车停站方案。
3.1 解的表达形式算法初始解构造
列车开行方案由所有列车的开行信息构成,因此问题的解Ω为
(19)
式中:Hf为列车f的开行信息。
(20)
(21)

通过Hf的前|S|个变量就可确定列车起讫点、停站方案,由于区间运行时分均为定值,因此通过始发时间和停站方案就可推算列车f在各停站的到发时刻。
内层算法初始解采用站站停模式;外层算法初始解可利用文献[14]的方法进行构造,因篇幅所限,这里不做详细描述。
3.2 算法邻域构造
(1)内层算法邻域构造
停站方案(即Hf中前|S|个变量)是由0-1变量所构成,因此可利用在列车起讫点间非始发终到车站对应变量取反方法构造停站方案的邻域。如图4所示,列车f在其行驶路径上,随机选择车站2进行变量取反而获得邻域解。
(2)外层算法邻域构造
外层退火算法的邻域构造方法如下[14]:
①删除列车:检查所有列车弧段客座率,若最高客座率低于规定阈值,则删除该列车。
②添加列车:在满足约束前提下,对于未登上车的客流,按照初始解构造方法生成站站停的列车;对于每个区间,若所有列车在该区间客座率的平均值达到规定阈值,则添加1列车,其停站方案与客座率最高列车相同,始发时刻亦安排在该列车所在始发时段内。
③拆分列车:检查所有列车弧段上的客座率,删除低于规定阈值的弧段,并根据车站等级、发车间隔时间确定拆分后列车的始发终到站和发车时刻。如图5所示,列车f由车站1运行至车站4,为站站停,其中车站1、2、4均可始发终到列车,由于车站1至车站2之间客座率为10%低于预设阈值30%,故将列车f改为由车站2始发。

图5 拆分列车示意图
④拼接列车:对于方向相同的两列列车f1与f2,若列车f1在车站s终到的同时列车f2也在车站s始发,并且f1在车站s的到达时间与f2在车站s的发车时间间隔不超过预设值,且拼接后的列车满足约束条件,则列车f1与f2进行拼接,新列车始发时间与f1相同,停站方案不变。
⑤调整列车始发时刻:在满足约束前提下,以一定概率将列车的始发时刻提前或推迟一定时间。
3.3 算法步骤
根据以上分析,可设计双层SA算法具体步骤如下:
(1)外层SA算法
设置初始温度值T0、温度下降比例θ,终止温度Tend,当前温度T=T0,迭代次数K=1。
Step1生成初始解Ω0,并设置当前解Ω=Ω0。
Step2计算目标函数。通过开行方案Ω确定列车与旅客所经弧段,计算目标值Z。



Step6迭代次数检验。K=K+1,若K>Uiner,Uiner为迭代次数上限,则令T=T×θ;否则转Step3。
Step7算法终止检验。若T (2)内层SA算法 以沪宁城际铁路下行方向的本线列车开行方案为研究对象。沪宁城际线是连接华东两大城市上海与南京的城际铁路客运专线,运营里程301 km,沿线共设车站23个,其中南京南站通过仙林联络线接入沪宁城际,上海虹桥站通过虹安联络线接入沪宁城际,区间运行时分根据现有的列车运行图获得,区间和车站信息见图6。 根据线路结构特点,可将南京站、南京南站合并为南京站,上海站、上海虹桥站、上海西站合并为上海站,客流信息也做相应处理。对于当日无到发客流的丹徒站、南翔北站也不予考虑。经上述处理后的线路共18个车站。考虑除南京站和上海站之外,常州站、无锡站、苏州站同样具备车底检修和夜间存车条件,因此将这5座车站设置为始发终到车站,即所有列车均在上述车站完成始发终到。 图6 沪宁城际铁路下行方向区间里程及运行时分 选取2017年5月31日沪宁城际的客流和运行图进行计算分析。其时沪宁城际下行方向运行本线车55列,客流需求总量为75 659人,所有列车定员统一为Mf=1 230,并将当前所购车票出发时间视为旅客期望出发时间。设定铁路运营时段为[05:00,24:00],客流时段划分为1 h。时空网络中时间间隔σ=2 min,这样每个车站共有571个离散时间点。根据现有列车运行图,车站最小发车间隔时间为6 min。另外根据文献[14],目标函数加权参数可分别设为δ1=6 000,δ2=1,δ3=50,δ4=100。 SA算法中参数T0=1 000,θ=0.98,Tend=0.001,Uiner=300。外层SA算法构造邻域策略中,删除列车阈值为0.5,添加列车阈值为0.7,拆分列车阈值为0.2,拼接列车阈值为10 min,调整列车始发时间概率为0.5,调整量为10 min。 根据所提出的时空网络优化方法,计算得到如图7所示的优化开行方案,相应的动车组列车的起讫点和开行数量见表1,停站方案基本信息见表2。 图7 沪宁城际下行方向优化列车开行方案 表1 列车起讫点和开行数量 与实际运行图相比,优化方案中列车总数减少19列,其中南京—上海和苏州—上海的开行列车数降低,南京—苏州、常州—上海和无锡—上海的开行列车数增加,由于短途列车始发时间可安排在线路中间车站出发旅客数量较多的时段,能有效降低短途旅客出发偏差时间,同时短途列车在弧段上运行时间更低,能更好的降低总成本,因此短途列车数量有所增加,而苏州—上海区间的部分旅客需求可以由常州、无锡始发的列车满足,列车数量也有所降低;列车平均停站数方面,优化方案相比实际方案增加3.1站,这是由于开行列车总数减少,为了使短途旅客能够得到列车服务,故列车停站数量有所增加。其中南京—上海区间里程最长,所能服务短途旅客数量最多,因此列车停站数量增幅最大,平均增加4.7站。 如表3所示,长途列车 (即南京—上海)在优化方案和实际方案中的列车始发时间分布都比较均匀;短途列车的始发列车多分布在前3个时段,且该时段内的优化方案比实际方案多出6列而达到26列,占到列车总数的72%。这主要是因为南京至上海之间增开较多的长途列车,可满足大部分的客流需求。短途列车主要分布在旅客需求较多的时空区域,即高峰时段[7:00,14:00],见图7。 表4所示为最优解与初始解的比较分析。相对初始解,最优解中开行列车总数、列车运行成本、旅客出行成本和旅客平均出发时间偏差,分别减少12列、1.11×107min、0.23×106min和增加0.15 min,平均客座率上升25.18%。时间偏差增加的原因,主要是由于初始解构造时更倾向于满足旅客出行期望,较少考虑运营成本因素,但算法会逐渐平衡企业和旅客两方面成本,故最优方案中企业成本下降,时间偏差增加,但偏差始终未超过20 min。 表3 优化方案/实际方案在不同始发时段的列车数量分布 表4 算法初始解与最优解比较 各时段旅客出发偏差平均值见图8,大部分时段的偏差值均在平均值之下,时段1出发时间偏差值较高主要是由于该时段出发人数较少;出发旅客数量最多的时段3的偏差值仅为15.1 min,说明在高峰时段的旅客需求能得到较好的满足。 图8 各时段旅客出发偏差平均值 图9展示了线路能力、客流和列车客座率随时间变化的情况。列车客座率大部分时段都达到80%以上,图中两端时段客座率较低主要是由于最早最晚时段内的客流较少。时段9中客座率有所下滑则是由于此时需求有所减少,但是大部分列车还未抵达终点站。图10展示了各区间运营时段内平均的断面客流量、区间运输能力和列车客座率情况。客流高峰出现在阳澄湖—上海区段,该区段内的客座率均达到86%以上。而且所有区间内列车客座率都在70%以上,运输能力得到较好的利用。 图9 线路能力、客流量和客座率 图10 平均区间运输能力、断面流量和客座率 列车开行方案是组织运用高铁运输能力的关键环节。利用时空网络方法研究考虑时变需求的高铁开行方案,可为开行方案决策者提供包括旅客期望出行时间等更多服务信息,从而提高列车开行方案的编制质量和系统的服务水平。本文在构造高铁开行方案时空网络的基础上,建立城际高铁列车开行方案的时空网络优化模型,以最小化铁路企业运营成本和旅客出行成本为目标,考虑时空网络客流及列车流守恒、发车时间间隔、列车定员、列车数量等约束,并结合问题特征设计了双层模拟退火算法进行求解。算例分析表明,所提出的方法计算快捷,结果合理,且与实际方案相比,优化方案在满足时变客流需求的前提下,降低了系统总成本,说明上述方法能为城际高铁列车开行方案提供科学决策支持。下一步工作将主要考虑动车组运用对列车开行方案的影响而开展协同优化研究。



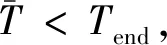
4 算例分析
4.1 算例数据

4.2 计算分析







5 结论
