特征标记依赖自编码器的多标记特征提取方法*
2020-03-19程玉胜李志伟庞淑芳
程玉胜,李志伟,庞淑芳
1.安庆师范大学 计算机与信息学院,安徽 安庆246011
2.安徽省高校智能感知与计算重点实验室,安徽 安庆246011
1 引言
随着大数据时代的到来,人们能从各种渠道获取大量的数据,但同时也带来了如何处理这些数据的问题,其中最常见的方法是对数据进行降维,主要包括特征选择和特征提取。目前特征选择研究较多,但相对于特征选择而言,特征提取可以通过原始数据集进行适当变换,得到更有效更有用的低维特征[1-5]。目前已经有很多经典的特征提取方法,如主成分分析(principal component analysis,PCA)[6]、方向梯度直方图(histogram of oriented gradient,HOG)[7]、线性判别分析(linear discriminant analysis,LDA)[8]、潜在语义索引(latent semantic indexing,LSI)[9]等。
相比于传统的单标记问题,经典的分类建模方法取得了不错的成果,而关于多标记分类问题,往往可以利用标记之间相关信息有效提高分类器的性能。但目前多标记学习仍存在三大挑战。其一,在单标记学习中,各示例标记分类相互排斥不存在共生关系,而对于多标记学习则各标记之间存在相关性,如何利用标记之间的相关性对多标记分类精度的提高尤为重要[10]。其二,在多标记学习中,数据特征往往具有较高的维度,而高维特征可能导致“维度灾难”,严重影响分类器的分类性能。其三,在多标记学习中各标记与其特征具有关联性[11-12],如何挖掘此类信息也是多标记学习中难点之一。为此大量学者提出了各种多标记分类学习方法,如类KNN(K-nearest neighbor)方法[13]、集合分类器和集成学习技术[14-16],大多数已被广泛地应用。
但是上述方法主要采用特征选择的方法进行分类建模,由于该方法通常具有指数级时间复杂度,一般不太适合高维数据分类建模。目前,多标记学习中数据一般具有高维性特点,因此如何处理这些高维数据,相关研究成果相继被提出。例如:MLSI(multi-label informed latent semantic indexing)[17]扩展了单标记无监督潜在语义索引(LSI)来处理多标记特征提取问题,通过引入权重来构建一个新的特征-标记信息的函数;文献[18]利用LDA 方法进行多标记特征降维处理,但是并没有有效利用标记与标记之间的相关性;文献[19]提出了多标记线性判别分析(multi-label linear discriminant analysis,MLDA)方法,在LDA 的基础上进行了优化,利用了标记与标记之间的关系,但是在实际中的性能受到了标记数量的影响;文献[20]基于希尔伯特-施密特独立标准(Hilbert-Schmidt independence criterion,HSIC)提出了基于最大化依赖的多标记维度约简方法(multi-label dimensionality reduction via maximum dependence,MDDM)。MDDM
的主要目的是通过使特征-标记之间的依赖度达到最大而得到最适合实验数据的投影矩阵,但是该方法并没有充分获取特征的信息,也没有考虑特征-特征、标记-标记的内在联系。
基于此,本文提出了一种基于特征标记依赖自编码器的多标记特征提取方法(multi-label feature extraction method relied on feature-label dependence autoencoder,MIMLFE)。主要包括:(1)使用核极限学习机自编码器将标记空间与原特征空间融合并产生重构后特征空间;(2)结合主成分分析与希尔伯特-施密特独立准则分别提取“特征-特征”和“特征-标记”信息;(3)使用多标记K近邻算法(multi-labelKnearest neighbor,ML-KNN)分类器进行分类。通过Yahoo 数据集中的11个子数据集上的结果与相关对比算法比较表明,本文提出的算法在多个评价指标上大部分优于这些方法。在算法介绍结束后给出了本文的伪代码。
2 基本理论研究
2.1 核极限学习机
极限学习机(extreme learning machine,ELM)[21-24]是一种单隐层前馈神经网络。相比于传统神经网络算法需要较多的网络参数设置可能出现局部最优解而无法得到全局最优的问题,极限学习机的主要特点在于学习速度快并且效果相较之前的神经网络也有着很大的提高。该网络在求解时只需设置隐藏层节点数并随机初始化权值和偏置就可以以较快的速度得到全局最优解。ELM 求解单隐层前馈神经网络可分为两个阶段:随机特征映射和线性参数求解。
在求解之前需要先做出以下定义:设有N个随机样本{(Xi,Yi)|i=1,2,…,N},其中特征空间与标记空间可分别表示为Xi=[xi1,xi2,…,xin]Τ,Yi=[yi1,yi2,…,yim]Τ,对于具有L个隐藏节点的单隐藏层神经网络形式化定义为:

式(1)中,βi=[βi1,βi2,…,βim]Τ表示输出权值,gi表示第i个隐藏节点的输出,而gi实质为激活函数,并可表示为:

式(2)中,Wi=[wi1,wi2,…,wim]Τ为输入权值,bi表示为第i个隐藏神经元的偏置,∙表示为点积。通常式(1)用来建模回归,而对于分类问题可使用sigmoid 函数来限制输出值的范围,从而达到分类效果。
以上为ELM 的第一阶段即随机特征映射,对于第二阶段的线性参数求解,通过最小化平方误差的近似误差来求解出连接隐藏层和输出层的权值β可表示为:

其中,H为隐藏层输出矩阵:
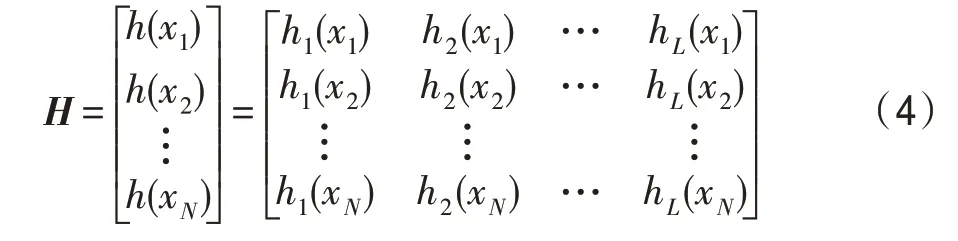
Y为训练标记矩阵:

通过式(1)和式(3),最小二乘解为:

其中,H†表示H的Moore-Penrose 广义逆矩阵,表示为:
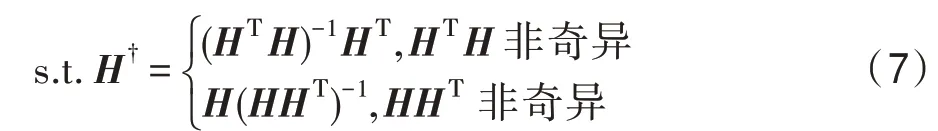

2.2 主成分分析
主成分分析是一种统计方法,是一种简化数据集的技术,是一个线性变换。这个变换把数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。主成分分析经常用减少数据集的维数,同时保持数据集的对方差贡献最大的特征。同时无监督范式下最流行的线性特征提取方法之一,无监督的方法是在不使用标签标记信息的情况下提取少量特征来保留尽可能多的判别信息,基于最小化平方重构误差来寻找最优投影矩阵。主成分分析可表示为以下最小二乘问题:
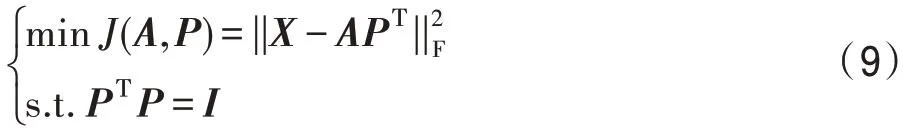
其中,F 表示矩阵的Frobenius 范数,P∈RD×D是投影方向矩阵,A∈Rl×D表示投影系数矩阵。通过约束PΤP=I,限制投影方向(即P的列向量)是正交的。

其中,tr()是矩阵的轨迹,通过使用∂tr(XA)/∂A=XΤ和∂tr(AΤA)/∂A=2A,然后设定J(A,P)对A的导数为零,得到并插入J(A,P),目标函数(10)就可以简化为:
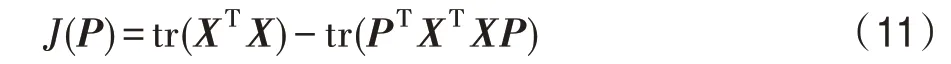
因为tr(XΤX)是常数项,最小化J(P)的问题就可以等价于最大化tr(PΤXΤXP),所以式(9)可以转化为:

通过拉格朗日乘数技术,将该问题转化为如下特征值问题XΤXP=ΛP,其中Λ是一个对角矩阵的特征值(λ1,λ2,…,λD≥0)。
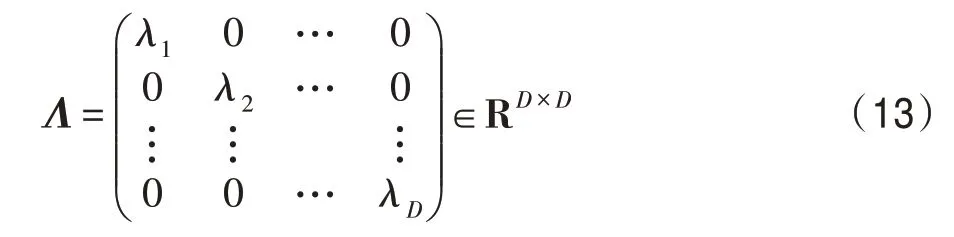
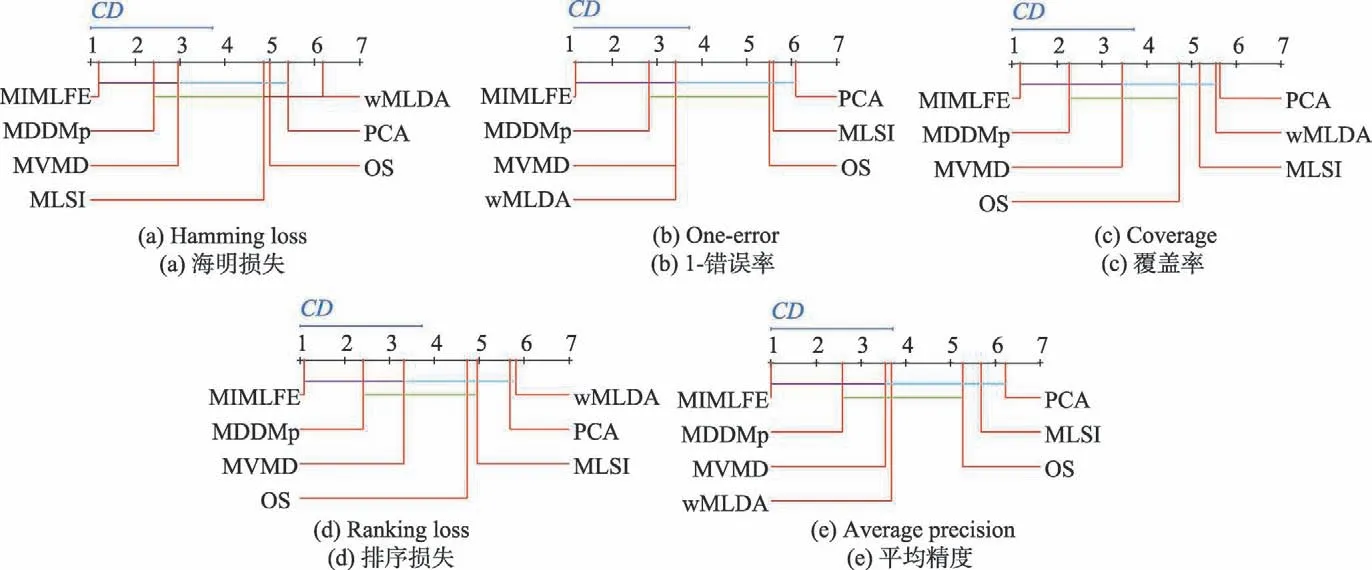
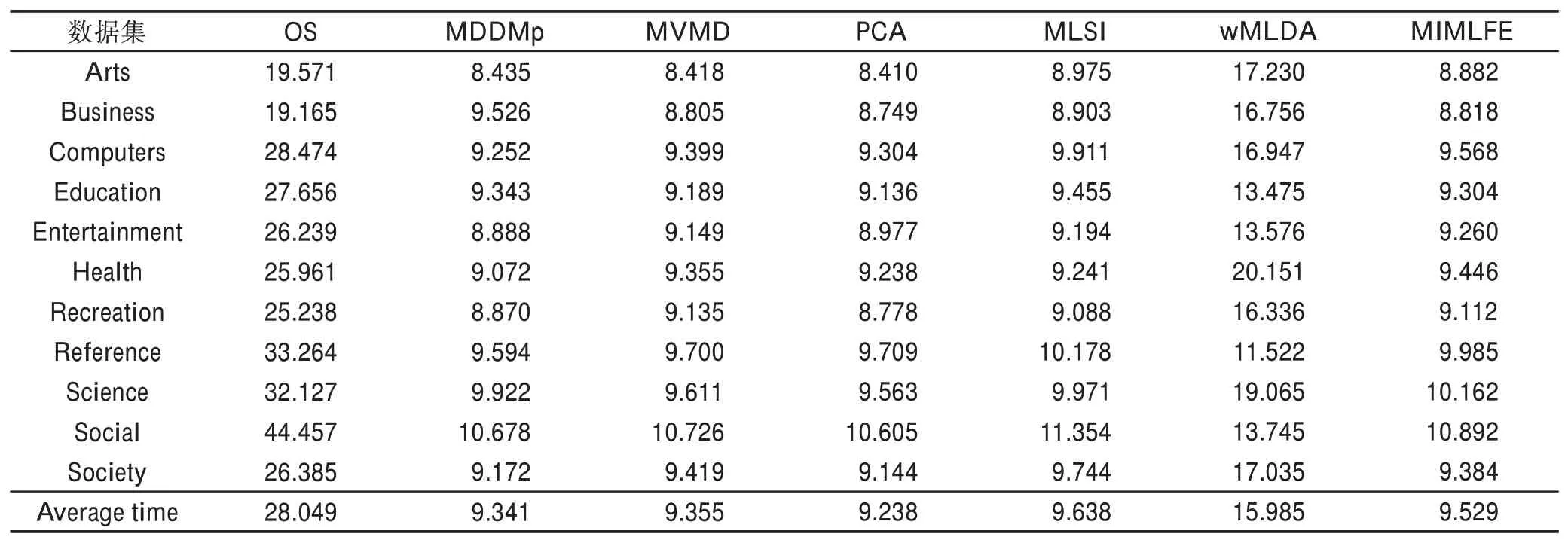
映射矩阵P是由相应的特征向量组成,主成分分析投影系数矩阵A的协方差矩阵是ATA=PΤXΤXP=Λ。说明主成分分析投影系数是不相关的。然后可以将式(11)转化为J(P)=tr(XΤX)-tr(Λ)。为了使J(P)最小化,选择d( 其中,t∈(0,1)是一个合适的阈值,用于衡量保存原始数据的信息。 Hilbert-Schmidt 独立性标准(HSIC)是一种非参数依赖性度量,它考虑所有变量之间的所有依赖关系模式。对于特征空间和标记的线性核,HSIC 的经验估计被描述为: 其中,tr()表示的是矩阵的轨迹,K和L分别是示例和标记对应的核矩阵。H用于除去均值IN表示大小为N×N的单位矩阵,eN表示所有的元素都是1,长度为N的列向量。如今通过MDDM 方法HSIC 已经成功应用在多标记特征提取上,忽略常数项(N-1)-2得到目标函数: 其中,P是线性变换矩阵P∈Rd×t,MDDM 的主要目的是通过使特征-标记之间的依赖度达到最大而得到最优的映射矩阵P,此方法已经在文献[25-26]中得到验证。具有正交投影方向的MDDM 的原始优化问题也被称为MDDMp[25]: 在现实世界中,真实的对象并不能如理论中那样简单,传统的单标记学习算法由于算法简单、对象单一而不能对现实中多语义复杂的对象进行有效准确的处理,也无法解决机器学习中的高难度问题,因此需要通过建立一个新的多标记学习框架来解决这一问题。对于任意的一个对象,通过向量来对其一个特征进行描述,再用这个特征向量对对象进行分类和类别标记。假定一个有N个样本的多标记数据集,X为n维的示例空间Rn,Y为m类标记空间,则在多标记学习中,给定数据集D={(x1,y1),(x2,y2),…,(xn,yn)},其中xi∈X是一个示例,yi∈Y是一组标记集合且,可得到映射关系f:X→2Y。 自动编码器(auto encoder)最早是由Rumelhart在1986年提出的,并成功用于处理高维度复杂数据,它的出现大大促进了神经网络的发展。自动编码器是一个由大于或等于3 层的神经网络组成,主要是输入层、隐藏层和输出层。自动编码器主要分为编码和解码两个过程。先将无标记的特征a输入到encoder 编码器得到输出b。这时候需要判别之前输入的a和b是否表示一致。这时就在输出后再加一个decoder 解码器,此时b就成为了解码器decoder 的输入,现在只要判断这个输出信号与之前的输入a的近似度就可以得到结论。如果这两个近似度很高,那么就有理由可以相信这个b是可靠的。因此在自编码器中需要不断调整encoder 与decoder 的参数使得重构的误差最小,此时的b就是原输入a的表示。 根据多标记学习的目标,同时结合ELM 学习模型和自编码器,多标记ELM 的输出函数H为: 为了使ELM 的输出h(x)β取得更好的分类结果,RELM 算法(regularized ELM)就是添加L2 正则来提高原始ELM 算法的稳定性和泛化性能,同时有效避免过拟合,目标函数表示为: 其中,ξi=[ξi1,ξi2,…,ξim]Τ,是训练样本Xi在m个输出节点的训练误差向量,C为正则化参数,根据KKT(Karush-Kuhn-Tucker)理论,可得: 其中,βj是连接隐藏层节点到第j个输出节点的权值向量,β=[β1,β2,…,βm],每个拉格朗日乘子αij对应于第i个样本的第j个输出节点,同时αi=[αi1,αi2,…,αim]Τ,α=[α1,α2,…,αm]Τ,可得到如下的KKT优化条件: 训练样本数N和隐藏层节点数L决定着隐藏层节点输出H的大小,将等式(21)和等式(22)代入等式(23),可以得到: U=(xN,yN)表示原特征空间xN与标记空间yN融合成的新的特征空间。此时,从等式(23)和等式(24)可得出ELM 的表达式为: 当N>L时,即当样本数量N大于隐藏节点数L时,可以从式(21)、式(22)和式(23)中得出ELM 另一种表达式为: 在ELM中,用户通常知道特征映射,如果用户不知道特征映射,则可以按如下方式定义ELM的内核矩阵: 此时,可得KELM 的输出表达式为: 目前,PCA 已经得到了广泛的应用。尽管现存的特征提取算法有很多,但是大部分不能有效利用“特征-特征”的信息,为此提出的方法希望既可以有效利用标记信息,又可以充分利用特征信息。第一,结合2.3 节的相关知识,采用了基于HSIC 与MDDM相同的目标函数,通过最大化XP与标记U之间的依赖度以获取“标记-标记”的信息;第二,利用PCA 的优点,降低维度约简中信息的损失。然后将PCA 中的目标函数与MDDMp 中的目标函数线性组合,最大化特征方差并同时最大化“特征-标记”依赖性。 其中,λ∈[0,1]是控制PCA 和MDDMp 两个平方误差项之间权衡的平衡因子,A和B表示两个投影系数矩阵,P表示投影方向矩阵。当λ=0 时,该模型退化为原始PCA,而当λ=1 时,模型就相当于MDDMp。然后对公式进行扩展: 在J(A,B,P)相对于A和B的导数为0之后,得到: 根据A和B上式可以化简为: 然后定义了一个新的向量: 带入得到J(P)=tr(G)-tr(PTGP),因为tr(G)是不变的,所以将问题转化为: 再利用拉格朗日定理转化为GP=ΛP,现在的目标函数为G(P)=tr(G)-tr(Λ)。意味着应该选择d维最大特征值及其特征向量来构造映射矩阵P。 算法伪代码如下: 算法1MIMLFE 算法 输入:X,N×n维样本特征空间;Y,N×m维样本标记空间;λ,平衡因子;t,特征值阈值;d,映射特征的维度。 (1)根据式(28)通过核极限学习机自编码器重构特征空间; (2)根据式(33)构造出矩阵G; (3)构造具有最大d特征值的n×d映射矩阵P; (4)ML-KNN 分类器分类。 为验证本文算法的有效性,从雅虎网站选取了不同的应用领域中的11个数据集(“Arts”“Business”“Computers”等)进行测试,各数据集的特征数目在400~1 100 之间,各数据集中包含2 000个训练样本以及3 000个测试样本,详细信息如表1 所示。 对于多标记学习,为有效验证本文算法性能,本文采用海明损失(Hamming Loss,HL)、1-错误率(One-Error,OE)、覆盖率(Coverage,CV)、排序损失(Ranking Loss,RL)[27]和平均精度(Average Precision,AP)作为评价算法性能的指标。 设多标记分类器为h(∙),预测函数f(∙,∙),排序函数rankf,多标记数据集D={(xi,Yi)|1 ≤i≤n}。上述5种评价指标HL、OE、CV、RL和AP具体定义如下: 海明损失用于估计样本在单个标记上被误分类的情况。公式中Δ 用于计算h(xi)和Yi的对称差。当HLD(h)=0 时为最好的情况,HLD(h)越小,分类器h(∙)的性能越高。 1-错误率度量标准用于评估排名靠前的标签在对象的正确标签集中的次数。即OED(f)越小,f(∙)的性能越高,当OED(f)=0 时为最好的情况。 覆盖率公式表示的意思就是所有文档中排序最靠后的真实标记的排序平均值,CVD(f)越小,f(∙)的性能越高。 排序损失表示的是相关标记与非相关标记进行两两对比,然后统计相关标记比非相关标记预测可能性小的次数。RLD(f)越小,f(∙)的性能越高,当RLD(f)=0 时为最好情况。 Table 1 Details of Yahoo data sets表1 雅虎数据集描述 平均精度用于考察在样本的类别标记排序序列中,排在给定样本标记之前的标记仍属于该样本标记概率的均值,APD(f)越大,f(∙)的性能越高,最优值为1。 对比实验代码均在Matlab2016a 中运行,硬件环境Intel®CoreTMi7-8700K 3.7 GHz CPU,16 GB 内存;操作系统是Windows 10。在实验中,每个算法的性能将由5个评估指标综合测量,各评价指标中↑表示指标数值越高越好,↓表示指标数值越低越好。实验采用OS(original set,表示原始ML-KNN 没有使用任何的特征提取算法的结果)、MDDMp、MVMD(multi-label feature extraction algorithm via maximizing feature variance and feature-label dependence)[26]、PCA、MLSI 和wMLDA(weighted MLDA)等多标记特征提取算法与本文算法MIMLFE 进行各指标对比。 在各对比算法的参数设置上,在MDDMp 中,设置为0.5。本文的实验使用ML-KNN 作为分类器,ML-KNN 值设置为默认值,即平滑系数设置为1,最近邻居数k设置为10。 为了更直观展示本文算法的有效性,本文在选取的11个数据集中每个数据集选取的特征子集数目占总数的10%,与所有对比实验的实验结果如表2~表6 所示。同时,随着特征子集数目的改变,针对评价指标AP,11个数据集在各个算法上的趋势情况如图1 所示,其他4个评价指标也可同样绘制此图,由于篇幅有限,省去未提。表7 给出各算法在11个数据集中实验的时间消耗。 Table 2 Results of Hamming loss↓表2 海明损失测试结果 Table 3 Results of one-error↓表3 1-错误率测试结果 Table 4 Results of coverage↓表4 覆盖率测试结果 Table 5 Results of ranking loss↓表5 排序损失测试结果 Table 6 Results of average precision↑表6 平均精度测试结果 Table 7 Comparison of computation time for algorithms表7 各算法的时耗对比 s 实验结果分析: (1)对 于Hamming Loss、One-Error 和Ranking Loss,可以发现在11个数据集上,其中有10个数据集取得最优值,即分类性能最佳。在数据集Computers上,MIMLFE 取得的Hamming Loss 值与最优Hamming Loss 值仅相差0.000 2。在数据集Business 上,MDDMp 算法在所有对比算法中取得的One-Error 最优值,MIMLFE 取得的One-Error 值比最优值仅高0.002。在数据集Social 上,ML-KNN 取得了最优Ranking Loss值。 (2)对于Coverage,MIMLFE 在9个数据集上取得最小Coverage 值。另外两个数据集在MIMLFE 上取得Coverage 值与最优Coverage 值最大仅相差0.083 0,最小仅相差0.020 7。实验结果进一步表明本文算法在绝大部分数据集上占优。 (3)对于Average Precision,MIMLFE 在11个数据集上取得Average Precision 值都是最大,这充分表明本文所提出算法的有效性。 (4)图1 为MIMLFE 算法在11个多标记数据集上以Average Precision 为指标的特征趋势图,可发现MIMLFE 选取的特征子集在特征总数的10%本文算法MIMLFE 比所有对比算法都占优。随着特征子集数量的增加,MIMLFE 在大部分数据集上效果都占优。进一步说明该算法性能占优。 各算法在多个数据集实验的时间消耗如表7 所示,本文提出的算法MIMLFE 运行的时间消耗明显比OS 和wMLDA 少,MIMLFE 和其他4个对比算法的运行时间基本相差不大,但是性能明显占优。进一步表明本文算法MIMLFE 的有效性。 为了进一步验证本文算法的有效性,运用统计学知识,在11个数据集上采用显著性水平为5%的Friedman test[28]检验。对于每个评价指标,都拒绝零假设,若两个算法在所有数据集上的平均排序的差高于临界差(critical difference,CD),则认为它们有显著性差异;反之则两个算法没有显著性差异。图2 给出了所有算法在不同评价指标上的比较,坐标轴画出了各种算法的平均排序,并且坐标轴上的数字越小则表示平均排序越低,相同颜色线段连接则表示两种算法性能没有显著差异。根据式(35)可计算出CD值为2.205 2。 对某个任意算法,都有30个结果作为对比(在5个评价指标上具有6个对比算法),通过图2 可以得出:(1)MIMLFE 在5个评价指标上与其他6个对比算法相比时排序均为第一。(2)在Hamming Loss、Coverage 和Ranking Loss 三个评价指标上,MIMLFE与MDDMp 和MVMD 均无显著性差异,但均优于OS、MLSI、PCA、wMLDA。(3)在One-Error 评价指标上,MIMLFE 优 于OS、MLSI、PCA。(4)在Average Precision 指标上,MIMLFE 与MDDMp 取得了相当的性能,但均优于其他所有对比算法。 Fig.1 AP trend chart图1 AP 趋势图 Fig.2 Performance comparison of algorithms图2 算法性能比较 特征提取是针对处理高维数据进行降维的一种有效方法。主成分分析(PCA)和特征标记依赖度(MDDM)是减少多标记维度的两种有效的多标记特征提取技术,前者已经与最小二乘法相关联。在本文中,利用核极限学习机自编码器,将原始的特征空间与标记空间融合重构,得到新的特征空间。然后推导出具有正交投影方向的MDDM 的最小二乘公式,利用线性组合方式组合这两个最小二乘公式,从而构建一种新颖的多标记特征提取方法,分别提取“特征-特征”“标记-特征”的信息以最大化特征方差和特征标记依赖性。实验结果表明了本文提出的MIMLFE 算法具有不错的效果和较好的稳定性。
2.3 基于依赖最大化的多标记维数约简
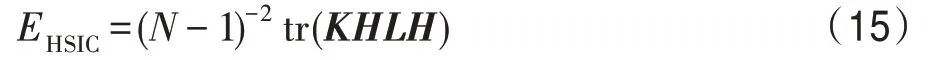
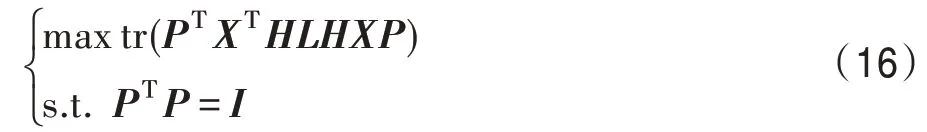
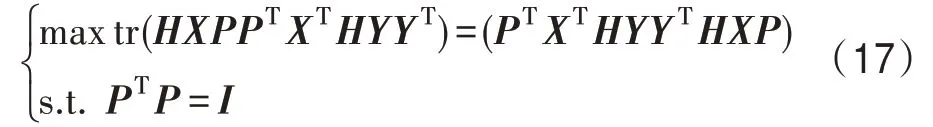
3 特征重构的多标记特征提取
3.1 基于KELM(kernel ELM)自编码器的多标记特征重构

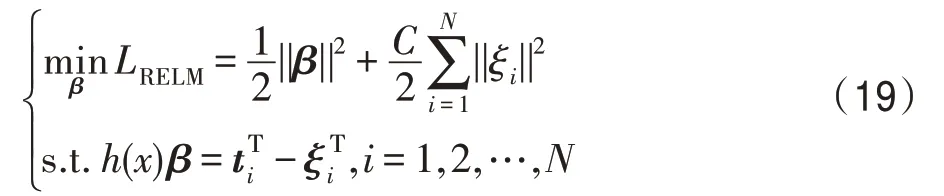
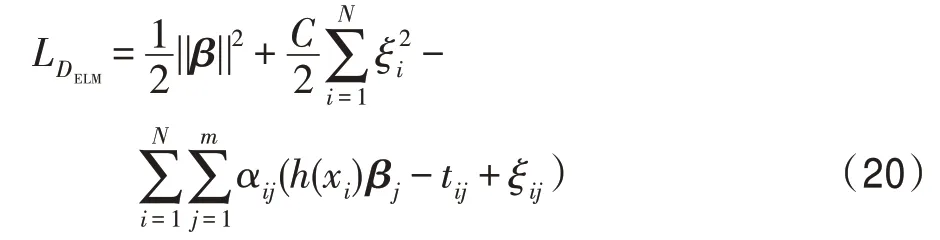

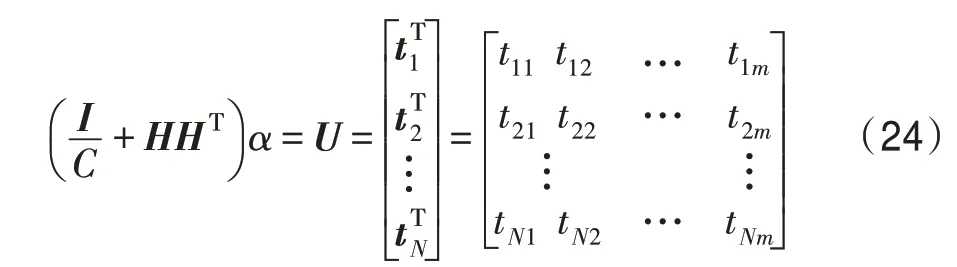
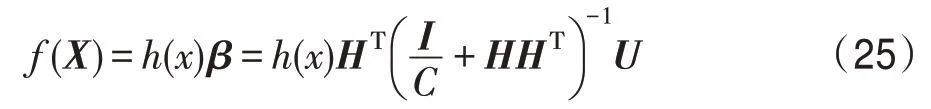


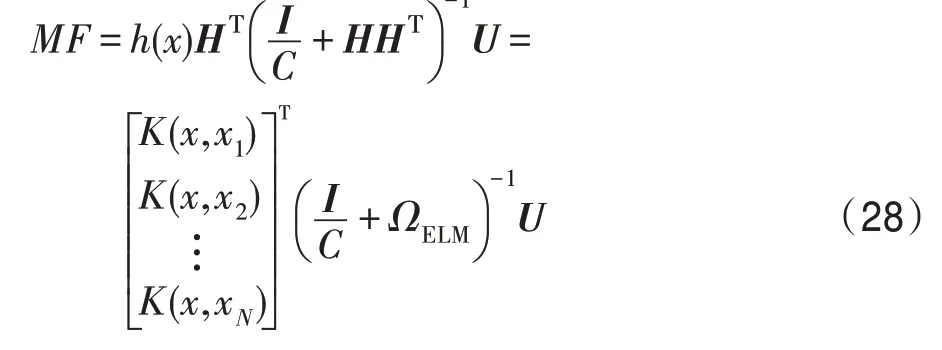
3.2 结合PCA 与HSIC 的多标记特征提取
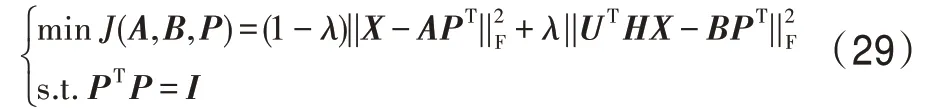
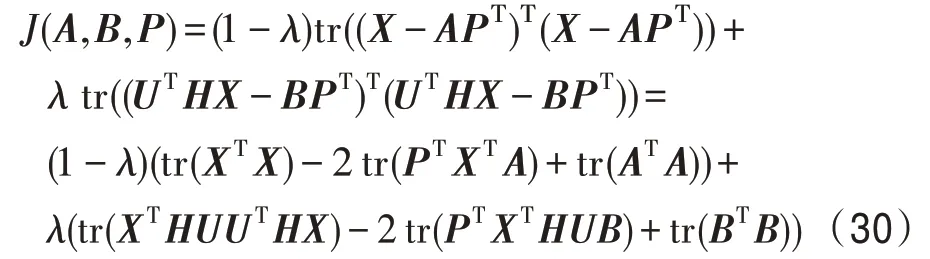

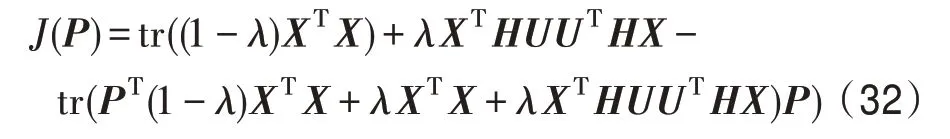
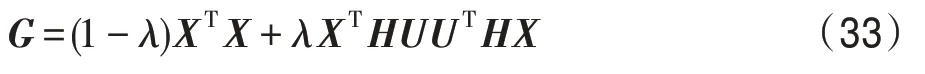

4 实验方案及结果分析
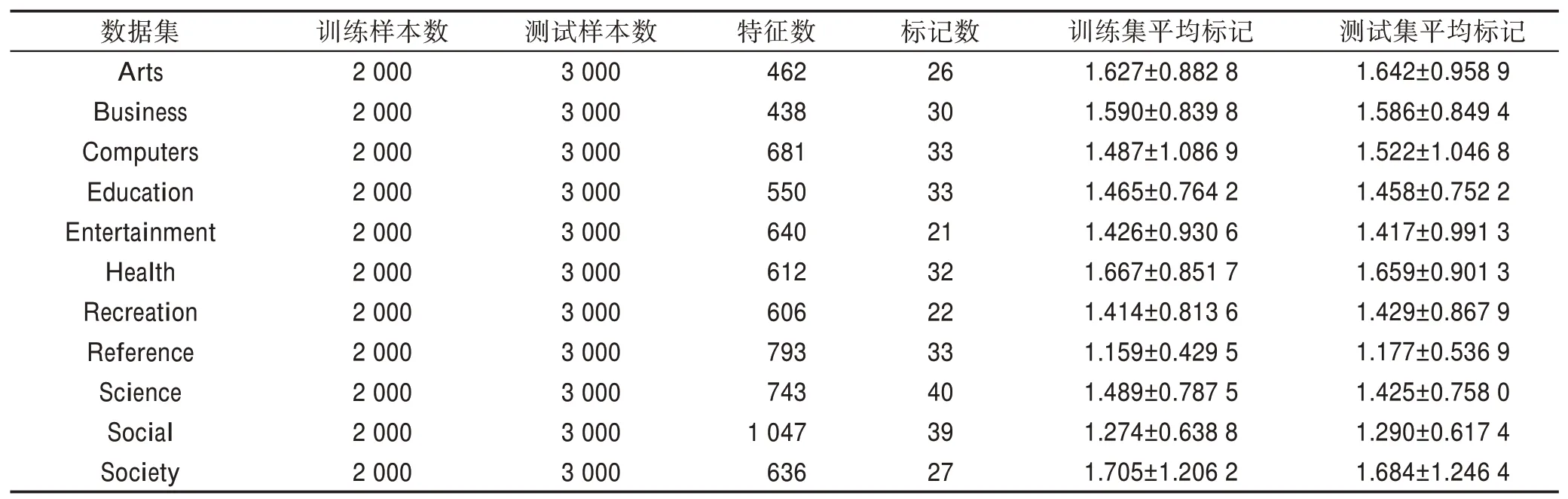
4.1 实验数据及评价指标描述
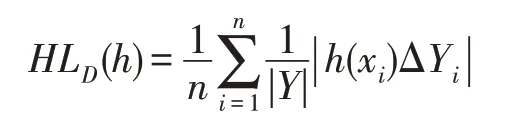
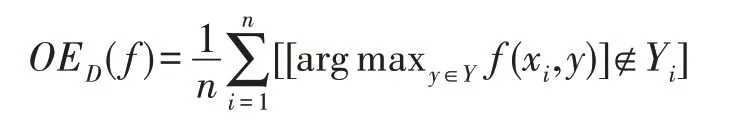


4.2 实验方案及参数选取
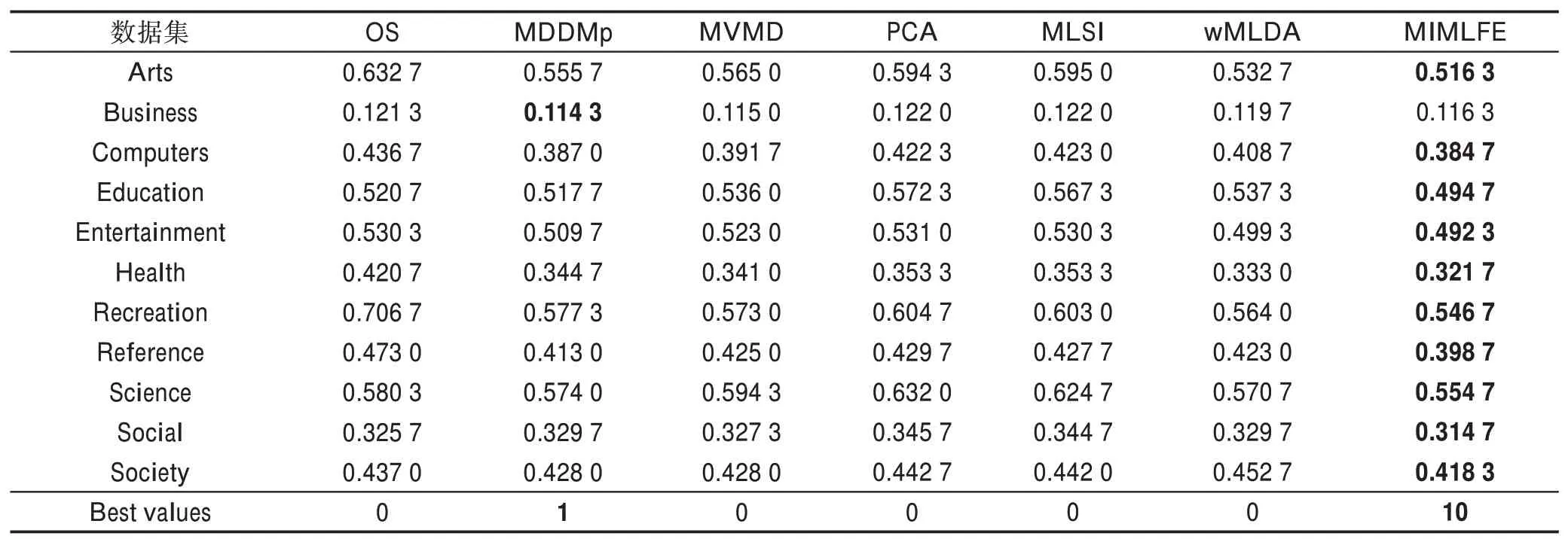
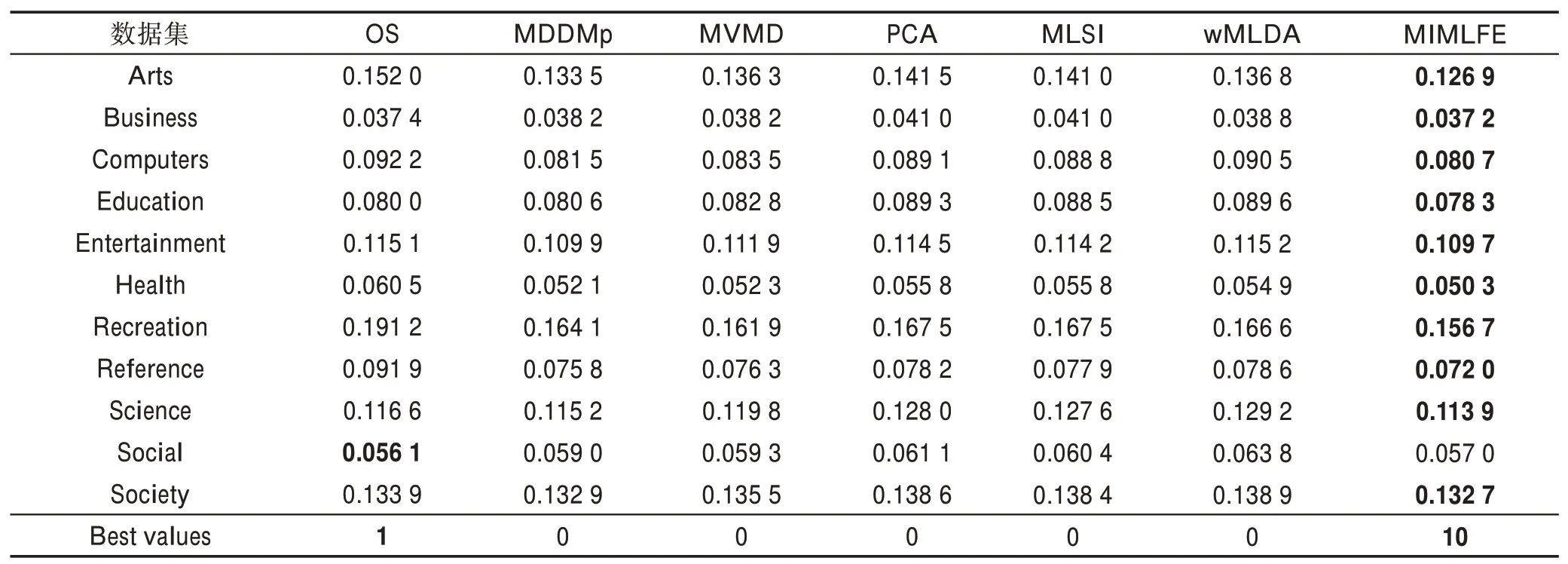
4.3 实验结果及分析





5 总结