一种纬度估计算法优化及误差抑制技术研究

刘 洋，莫明岗，张吉先，郭玉胜，邓继权

(北京自动化控制设备研究所，北京 100074)

0 引言

通常情况下，惯导系统初始对准需要外部输入具有一定精度的当地地理纬度。然而对于航海用惯导系统，舰船在战时会遇到卫星信号受干扰等情况导致无法获取准确的当地地理位置信息，这就要求惯导系统具备舰船航行中自寻纬度的能力[1-3]。文献[2]提出了一种晃动基座纬度估计方法，通过惯性系下不同时刻重力加速度向量的夹角求取纬度，但该方法无法适用于动基座情况。文献[3]在该方法的基础上，提出了一种航行中纬度估计方法，通过引入计程仪辅助速度信息，补偿由于载体机动所产生的误差[4]。为降低惯性器件测量噪声的影响[5]，在计算过程中对测量的重力加速度进行积分以提高纬度估计精度[6]，但该方法对重力加速度积分时，积分区间的选择没有充分利用所有的测量信息[7]，使纬度估计精度受到一定影响。

本文提出了一种惯导系统行进中纬度估计算法优化及误差抑制方法，首先分析了纬度估计的主要误差来源。在此基础上，对重力加速度积分区间的选取进行推导并给出了最优积分区间的选取方式，充分利用了整个纬度估计时间内的所有采样信息，提高了纬度估计精度。另外针对舰船在航行中受到的外部扰动，采用最小二乘拟合的方式，对陀螺和加速度计的测量误差进行抑制，提高了舰船行进中惯导系统的纬度估计精度。

1 纬度估计方法

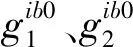
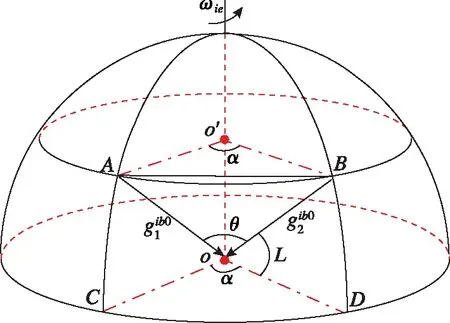
图1 海上航行中自寻纬度示意图Fig.1 Self-seeking of latitude in sea navigation

设对准初始时刻t1系统位于A点，经过一段时间，t2时刻系统位于B点。可以得到

|Ao′|=|Bo′|=|Ao|cosL

(1)

从而有

(2)

又因为

(3)

根据式(1)～式(3)可以得到

(4)

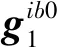
(5)

其中

(6)

(7)

可以得到

(8)

角度α根据时间t1与t2得到

α=ωie×(t2-t1)

(9)

式中，ωie为地球自转角速率。

2 纬度估计最优积分区间选取

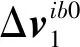
2.1 角度θ的最优区间分析

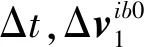
图2 积分区间示意图
Fig.2 Integral interval diagram

(10)

根据式(10)可将用于计算角度θ的速度增量记为

(11)

(12)

(13)

(14)

由式(14)可以分析出，为了使采样后方差变小，应通过增大分母的方式，这就需要扩大Δvib0的积分范围，将式(11)改为

(15)

(16)

从而

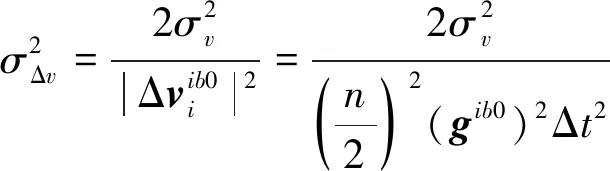
(17)

(18)

2.2 角度α的最优区间分析

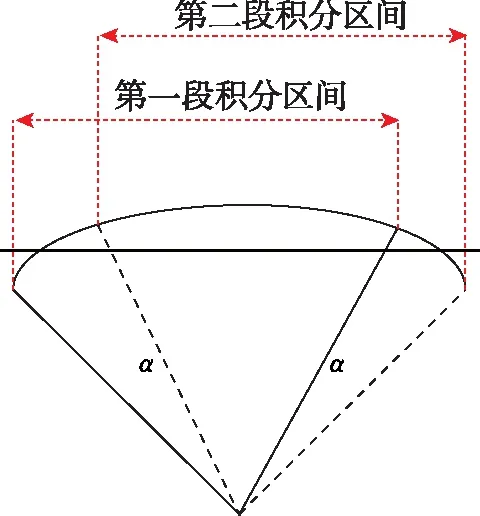
图3 积分区间与地球自转角α的关系Fig.3 Relationship between the integral interval and the rotation angle of the earth

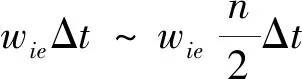
因地球自转角速度的数量级相对于速度增量很小，分母值过小会导致计算奇异[13]。所以为了提高估计精度，在分子固定的情况下尽量提高α，由图3可知,α的最大值是在2段积分区间刚好不交错时，即地球自转时间与重力加速度积分时间相等

(19)

3 外部扰动误差抑制

当船在行进过程中，由于载体受到外界环境或自身因素影响，如风浪、发动机振动等[14],使得惯导系统测量得到的地球自转角速度和重力加速度值相对于静基座的测量结果受到严重干扰，其中线振动干扰是一个重要环节[15]。

采用最小二乘算法对包含线振动干扰的速度矢量进行拟合，利用拟合结果进行姿态矩阵解算以抑制线振动干扰的影响。

由比力方程可知，对于速度模型

(20)

其中

(21)

式中，g0=9.780325。

惯性系粗对准一般在短时间内完成，这时可做如下近似

(22)

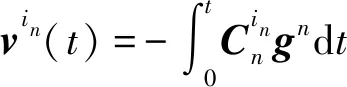
(23)

拟合后式(8)等价于

(24)

4 仿真验证

4.1 仿真条件

为模拟舰船在航行中的真实运动情况，假设典型海况下摇摆模型为

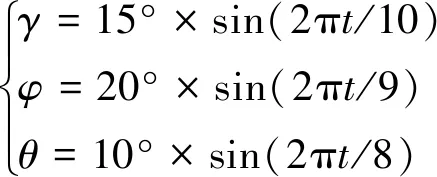
(25)

式中，γ、φ和θ分别为系统的横滚角、航向角和俯仰角，t为时间。

设舰船初始速度为10m/s，充分考虑惯导系统的器件精度以及电磁计程仪的测量精度，仿真中各项误差设定如所表 1示。

表1 仿真误差设置Tab.1 Simulation error setting

4.2 仿真结果

为了检验优化区间后对纬度估计精度的影响，分别在纬度20°、40°、60°和80°进行仿真，截取100条次数据进行验证(实际使用数据600s，每次读取数据起始点都向后推5s)，启动时间为100s。两种积分区间选取效果对比，虚线是优化积分区间，实线是采用了原方法，如图4～图7所示。

改进后的纬度估计精度有了较大的提高，取100条次仿真验证，纬度估计误差缩小0.3°以上，估计结果如表2所示。

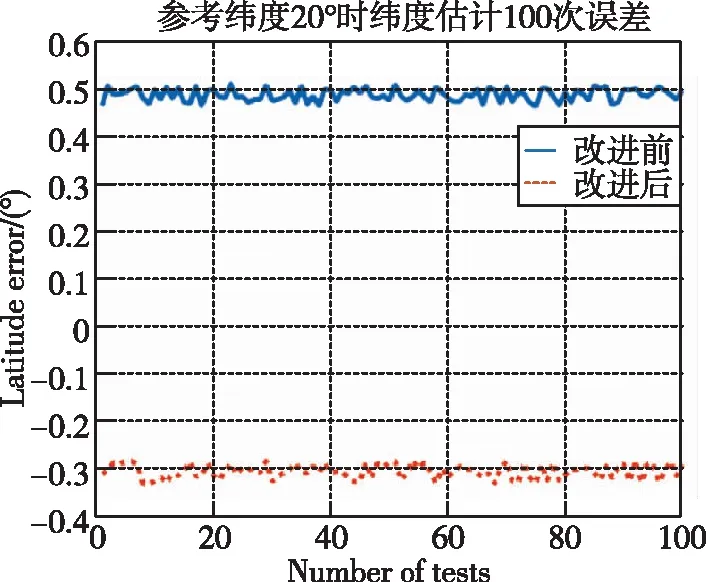
图4 20°时纬度估计仿真结果Fig.4 Latitude estimation simulation results at a reference latitude of 20°

图5 40°时纬度估计仿真结果Fig.5 Latitude estimation simulation result at a reference latitude of 40°

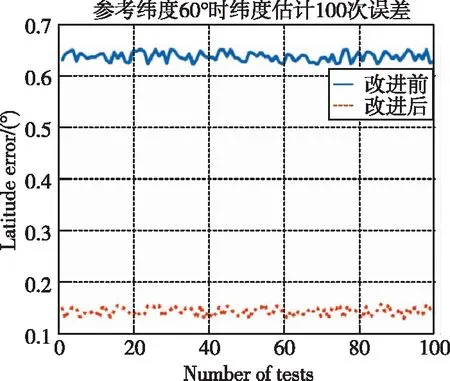
图6 60°时纬度估计仿真结果Fig.6 Latitude estimation simulation results at a reference latitude of 60°

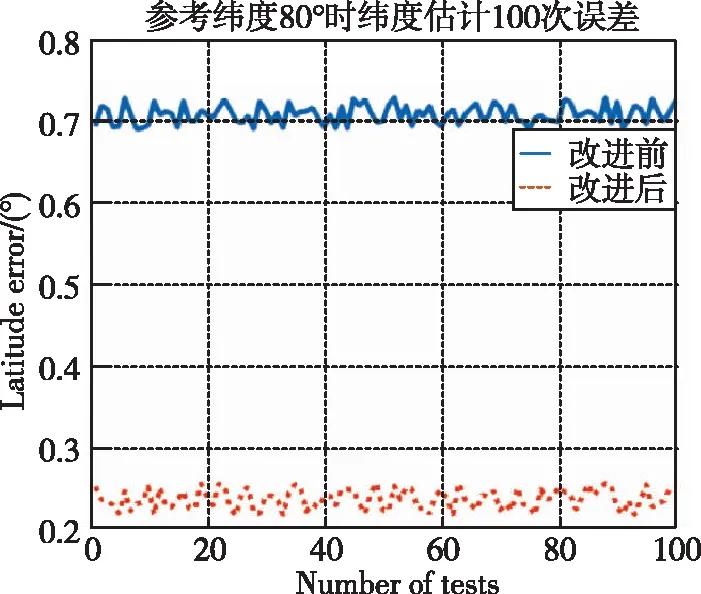
图7 80°时纬度估计仿真结果Fig.7 Latitude estimation simulation results at a reference latitude of 80°

表2 动基座下纬度估计结果Tab.2 Latitude estimation results under the moving base

4.3 车载试验验证

为了进一步验证算法的有效性，利用某型光纤捷联惯导系统车载数据进行仿真，所用惯导系统陀螺零偏0.01(°)/h，加表零漂100μg。跑车轨迹为匀速直航，速度约为10m/s。纬度估计时间为100s，截取100条次数据进行验证，纬度估计误差结果如图8所示。

经100次车载试验误差结果表明，采用优化的积分区间并对外部扰动误差抑制后的纬度估计均值从0.77°缩小到0.34°，如表3所示。

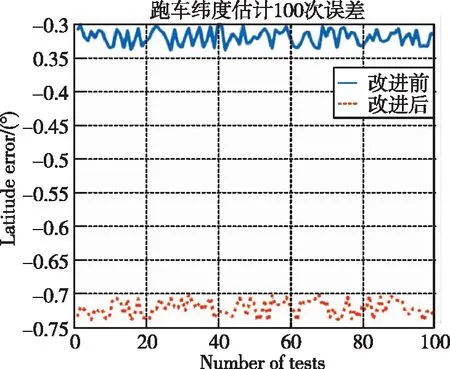
图8 纬度估计仿真结果Fig.8 Latitude estimation simulation results

表3 车载纬度估计误差Fig.3 Latitude estimation errors in vehicle experiment

5 结论

本文对捷联惯导系统纬度估计算法进行了优化分析，确定了最优的采样区间。同时采用计程仪补偿以及最小二乘三阶拟合的方法对外部扰动误差进行了抑制。纬度估计精度对舰船海上航行至关重要，理论仿真及车载试验结果表明，使用以上方法可以提高纬度估计精度。