基于GARCH 模型的多元控制图研究①

李 双，刘 浏，沈婉晴

一、 引言

统计过程控制控制(SPC)是一种重要的监控方法，它能够提高许多领域产品的生产质量包括工业、金融、经济、医疗保健、环境科学等领域，SPC 用千检测产品质量特征值发生变化的常用和主要工具是控制图。 常规的质量控制图主要有休哈特控制图、CUSUM 控制图以及EWMA 控制图。 休哈特控制图是休哈特博士在1924 年提出来的，它对检测大的漂移更有效，基于此Page 在1954 年提出了CUSUM 控制图，Roberts 在1959 年提出了EWMA 控制图，他们都对检测中小漂移有更加好的效果。 在一元EWMA 控制图的基础上Cynthia A. Lowry 等人在1992 年提出了多元情况下的EWMA控制图也就是MEWMA 控制图，MEWMA 控制图可以对多维随机变量进行监控，但也要求我们的观测值要满足独立同正态分布的假设。 在金融数据等数据中，很多都不满足MEWMA 控制图的假设前提，例如股票收盘价一般具有异方差性，如果我们忽视异方差性把它看作独立正态分布则控制图性能会大大降低。 ARCH 模型由Engle 教授在1982 年首次提出，ARCH 模型能准确地模拟时间序列的波动性。Bollerslev(1986 年) 在ARCH 模型的基础上提出了广义ARCH 模型(GARCH 模型)，GARCH 模型是应用最广泛的推广模型。 很多数据存在异方差性在对它们进行监控时可以先拟合GARCH 模型。 例如股票数据，先对其拟合GARCH模型再利用控制图进行监控。 已有的控制图方法都是对单只股票进行监控，无法实现对多只股票同时进行监控，但是很多股民通常都不会只买一只股票，而是同时持有不同的几只股票。 同时把多只股票放在一个控制图中进行监控，能够在较短的时间做出相应的决策，很大程度上节约时间并且规避因为没有及时做出决策而产生的风险。 本文提出利用GARCH 型MEWMA 控制图对多只具有异方差性的数据同时进行监控，并运用蒙特卡洛法得到的ARL 对控制图性能进行研究。 前人在对一元异方差的数据进行监控时， 使用条件异标准差替代观测值无条件标准差作为控制线标准差。 本文是针对多元情形，运用MEWMA 控制图同时对多组具有异方差结构的数据进行监控，在具有异方差性的数据中，利用它们各自的条件异方差作为MEWMA 控制图观测值的方差，通过蒙特卡洛法进行模拟，由结果可以看出在异方差情形下我们的方法效果较好。 应用我们的方法，能够同时对多只具有异方差性的数据进行在线监控，能为投资者提供更好的参考，有广阔的应用前景。

二、 MEWMA 控制图

Cynthia A.Lowry 等人在1992 年提出MEWMA 控制图，MEWMA 控制图可以同时对多个质量特征进行监控，它的模型如下。

假设观测值Xt＝(x1t，x2t，…，xpt)T，t＝1，2，…，n是拥有P个质量特征的P×1 维随机向量且Xt～NP(μ，Σ)，μ，Σ分别为观测值Xt的均值向量和协方差矩阵。

则MEWMA 统计量Qt构造为：

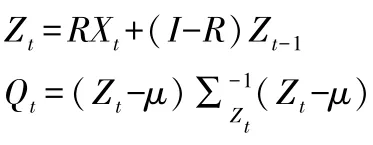
其中：R＝diag(r1，r2，…rp)当r1＝r2＝…＝rp时：

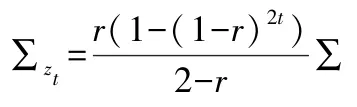
当t→∞时：

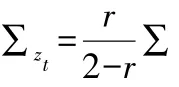
0＜ri≤1，i＝1，…，p当统计量Qt的值超出受控时的控制线UCL 时，控制图会给出报警信号，表明此时我们的观测值发生了漂移，控制线UCL 通常通过模拟得到。 衡量控制图性能的指标是ARL(Average Run Length)，一般受控时ARL 越大越好，失控时我们希望ARL 越小越好。 受控时的ARL 称为ARL0失控时为ARL1。

三、 GARCH 模型

当受控过程Xt{ }存在波动聚簇性时，我们可以对其拟合GARCH(m，n)模型。 其模型结构为：

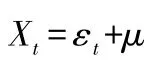
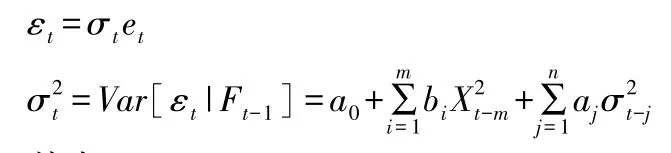
其中：

m(≥1)，n(≥0)，a0≥0，bi≥0，aj≥0 有a0，bi，aj是常数。et～WN( 0，1)且对于所有的t，εt与{Xt-k，k≥1}相互独立。 我们称为给定前期信息集Ft-1条件下{Xt}的条件异方差，在t时刻有Xt～N(μ，)它刻画了{Xt}的随时间的波动情况。 张力健等人在构造控制图过程中，以{Xt}的条件异标准差σt作为观测值标准差来构造控制限即得到ARCH 型控制图。 周丹等人把这种构造控制图的方法应用到了EWMA 控制图中，并取得了良好的效果。

四、 GARCH 模型的MEWMA 控制图

对具有异方差性的数据，先对其拟合GARCH 模型再利用多元控制图对它们进行同时监控。 为了方便我们以二元MEWMA 控制图为例，在异方差情形下的二元MEWMA 控制图模型可以表示为如下形式：

随机变量X1，t的模型为：

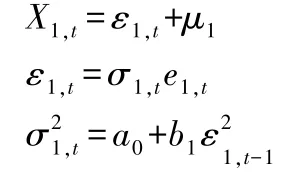
随机变量X2，t的模型为：

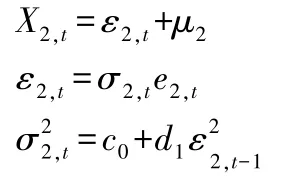
则统计量Qt构造为：

其中Xt＝(X1，t，X2，t)'，μ＝(μ1，μ2)'，e1，t与e2，t～WN(0，1)，μ是Xt的均值向量且X2，t的协方差矩阵，常规的MEWMA 控制图中∑是一个定值，但是存在异方差性的数据其方差是会随时间的变化而变化。先对观测值分别拟和GARCH 模型，在用它们的条件异方差和替代∑中随机变量各自的方差。

五、 举例论证

以二元控制图为例，在金融数据比如股票数据中，多支数据往往具有异方差性和相关关系，本节受控过程(Xt)与{Yt}具有异方差性且二者之间存在一定的相关关系Yt＝0.2Xt+0.05。

{Xt}的输出模型设为：

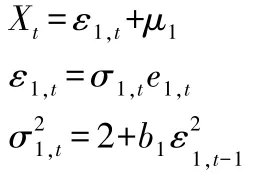
μ1，μ2分别是序列Xt{ }，Yt{ }的均值。 在b1取不同值情形下，给定Xt{ }的模型后，受控过程Yt{ }的模型由Eviews 软件拟合得到。 由应用R 软件，通过蒙特卡洛模拟法模拟一万次得到模拟结果。 固定ARL0当Xt{ }，Yt{ }均值同时发生漂移或者某一个变量的均值发生漂移时比较它们的ARL1，从而得到控制图性能。 确定受控时ARL0＝200，μ1＝0，ε1，1＝0，ε2，1＝0，在失控情形下ARL1越小越好。 选取控制图的平滑系数为r＝0.1，MEWMA 控制图要求数据服从多元正态分布故先对数据进行多元正态性检验，应用主成分分析法对{Xt}，{Yt}先进行二元正态性检验，在b1＝0，0.3，0.6，1 时检验的每组Q-Q 图分别如下所示。

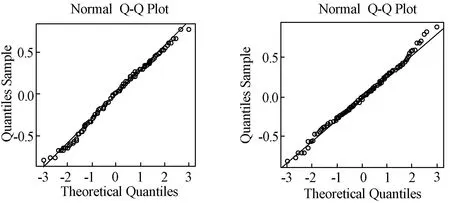
图1 b1=0 时Q-Q 图

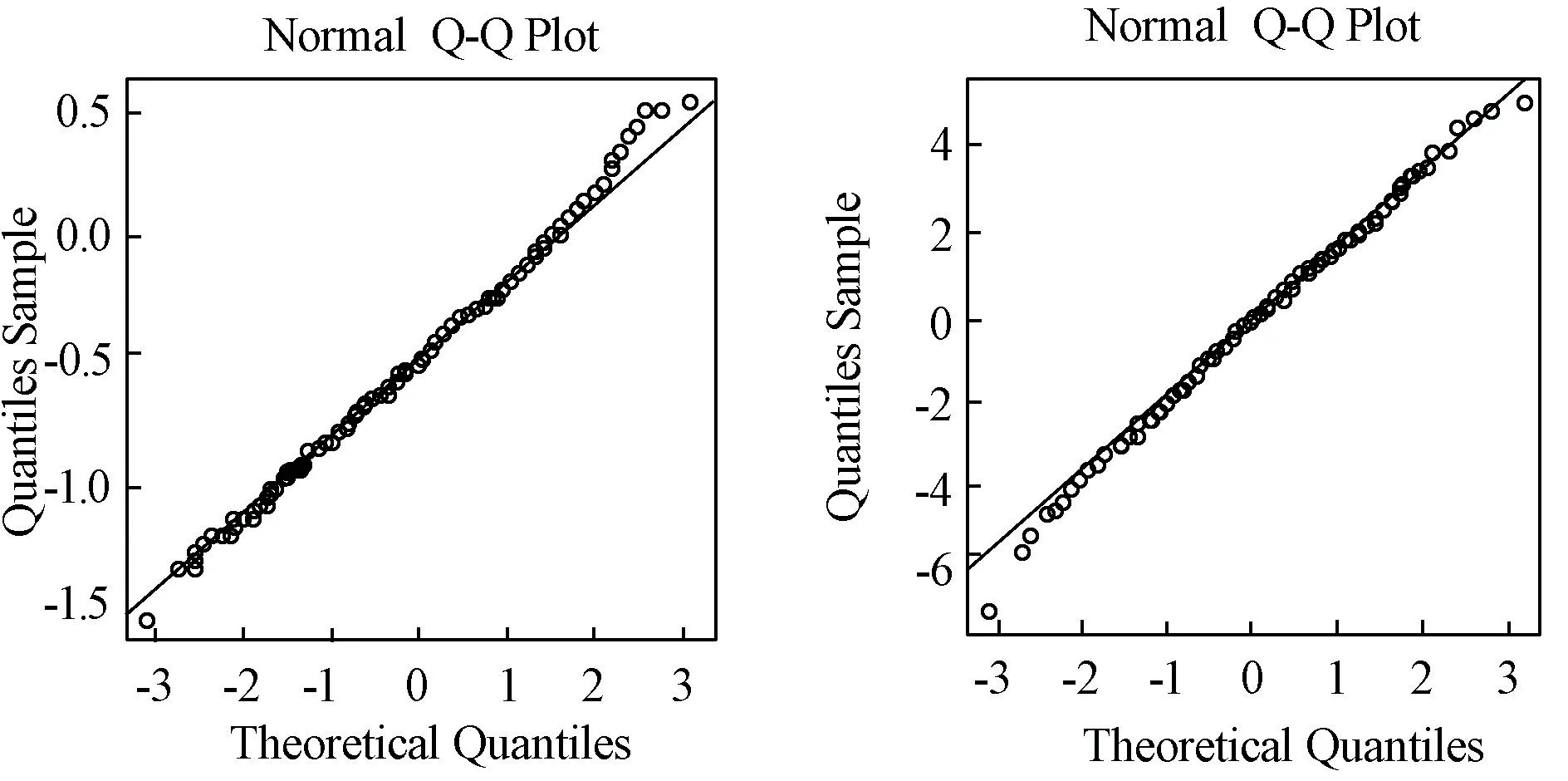
图2 b1=0.3 时Q-Q 图

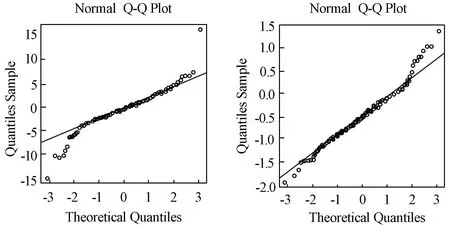
图3 b1=0.6 时Q-Q 图

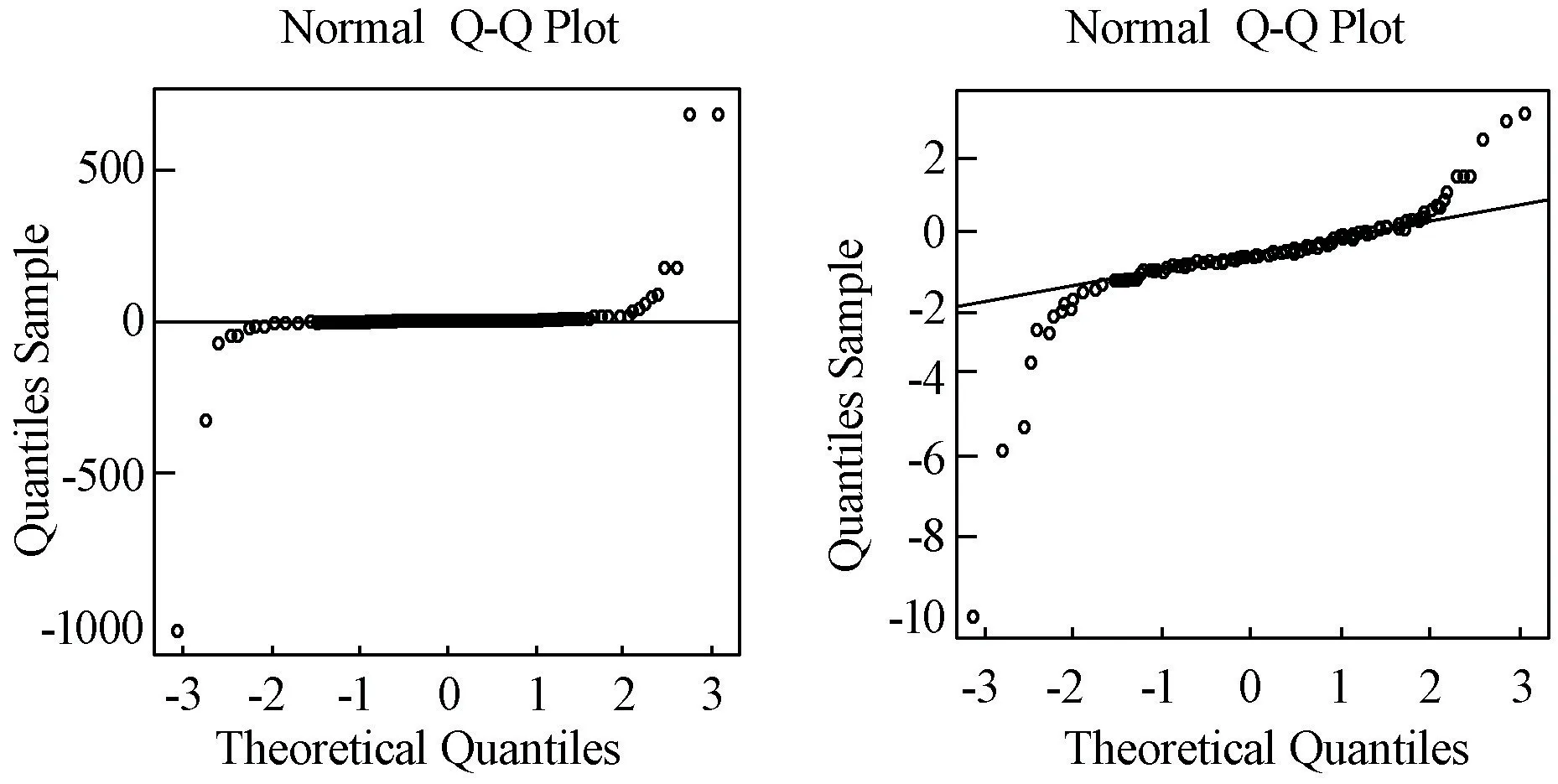
图4 b1=1 时Q-Q 图

由Xt{ }，Yt{ }的Q-Q 图可以看出不论b1取何值时都基本二元服从正态分布。Xt的均值为0，Yt的均值为0.05，因此可以建立二元MEWMA 控制图对Xt{ }，Yt{ }同时进行监控。以下是随机变量的均值发生不同漂移后的模拟结果。

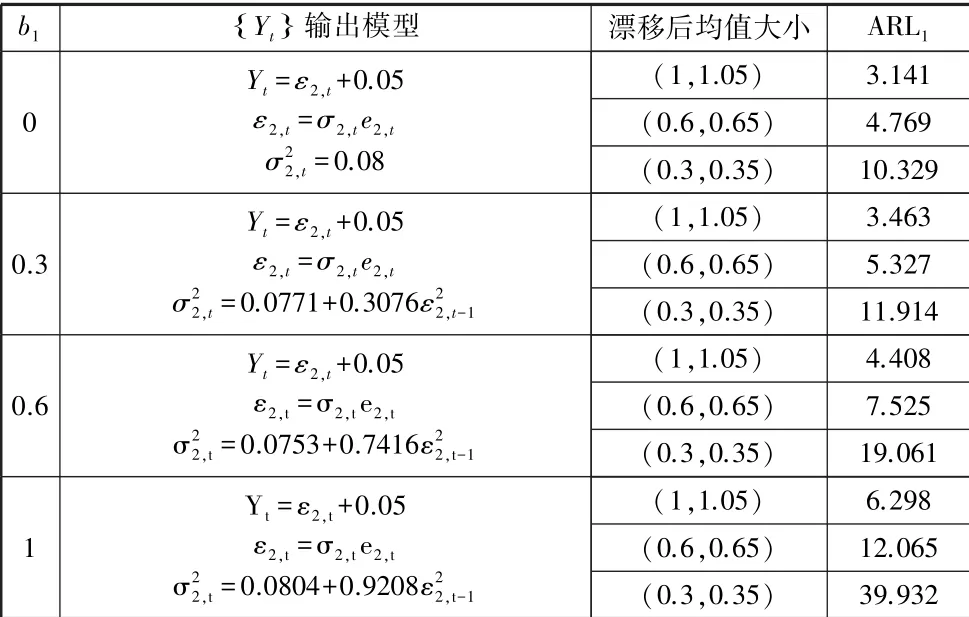
表1 在ARL0为200 时，b1取不同值下 Xt{ }， Yt{ }均值都发生漂移模拟结果

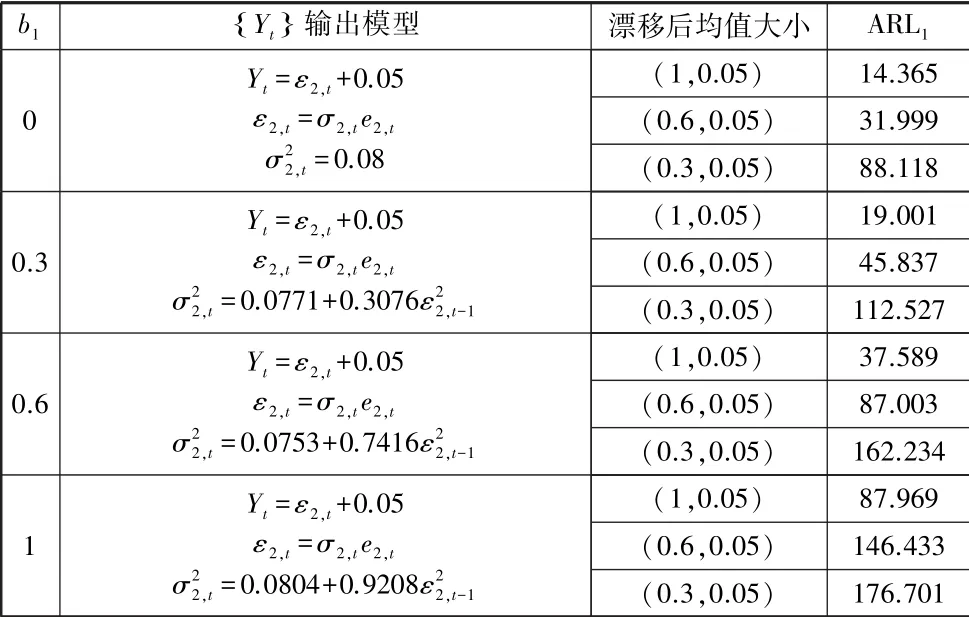
表2 ARL0为200 时，b1取不同值下Xt均值发生漂移模拟结果：

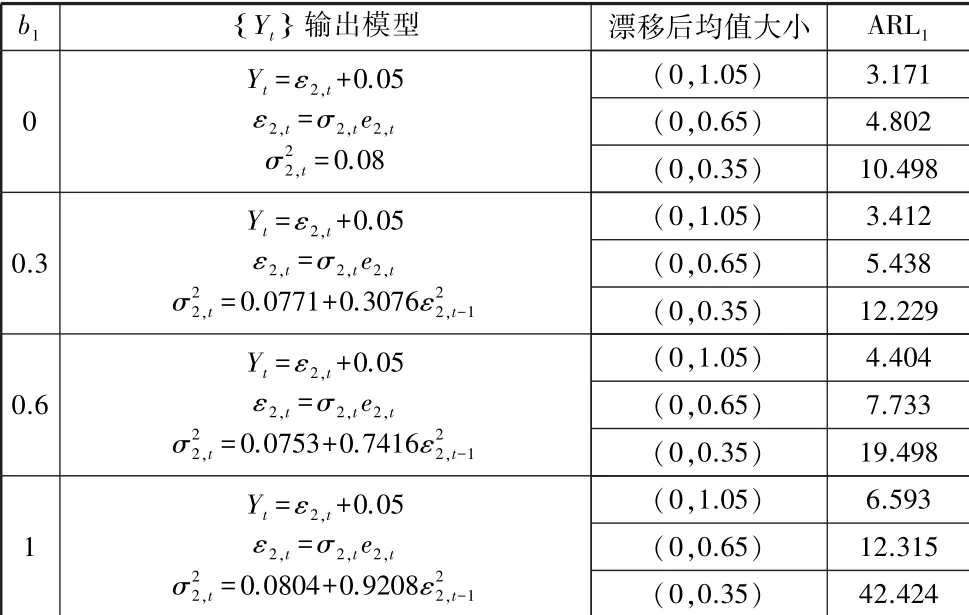
表3 ARL0为200 时，b1取不同值下Yt均值发生漂移模拟结果：

表1 到表3 都是运用R 软件进行蒙特卡洛方法随机模拟10000 次得出的结果，由模拟结果可以得出，随着b1的值不断增大不论是两个变量的均值同时发生漂移，还是某一个变量的均值发生漂移，控制图都能较快地给出报警信号，说明我们的方法是较好地。 特别是在两者均值同时发生漂移时和Yt发生漂移时，控制图效果很好能够较快地给出报警信号。

六、 结语

在运用控制图进行监控过程中，很多数据存在异方差性，研究者通常采用GARCH 模型刻画它的波动性，但是在以往的文献中大多都是对一元情形下的异方差性数据进行监控。 本文提出了对多元情形下存在异方差结构的数据进行监控的方法，即运用随机变量拟合的GARCH 模型的条件异方差替代随机变量各自的无条件方差作为协方差矩阵中各自的方差。 先检验了数据的多元正态性，再通过蒙特卡洛方法证明了我们方法的监控效果较好。 以此为基础构造控制图能够同时对多只具有异方差结构的数据进行监控，能够为投资者提供更多的参考。