基于改进k-means的电力信息系统异常检测方法

黄 林，常 健，杨 帆，李 忆，牛新征

1) 国网四川省电力公司信息通信公司，四川成都 610015; 2)电子科技大学计算机科学与工程学院，四川成都 611731

电力信息系统负责监控电网各平台的状态，保障电网各平台稳定运行. 面向电力信息系统数据设计精准高效的异常检测方案，有助于运维人员快速定位故障，提高运维效率.

异常点与正常发生的事件具有较大差异，极大可能是由非正常机制产生的数据点造成的. 传统基于规则的异常检测方法根据专家经验设置规则，检测系统的异常，依赖于预先定义好的数据指标特征. 但随着电力基础设施的升级、电力信息系统监控指标及主机数量的不断增长[1]，当面对大量的主机以及多样的采集指标时，阈值设置复杂，工作量呈指数增加. 因此，人工智能技术被更多应用于异常检测.k-means算法作为一种经典的数据挖掘方法，被广泛用于数据的异常检测[3-13].根据检测思想的不同，可分为两类. 一是将数据空间聚类，每一类别由人工标记为正常类或异常类，检测异常. 如马雪君[4]通过自适应遗传算法进行聚类，动态识别异常类，获取异常模式. 闫義涵[5]根据标准差与信息熵动态分裂簇进行聚类，识别异常. 该类方法的优点是能快速定位异常类别，但是由于异常类别难以枚举，异常类别可能增加，需要海量数据的支撑. 二是将数据空间聚类，识别数据空间中正常模式，然后判断样本点到正常模式的距离是否超过设置的阈值来检测异常. 如蒋华等[6-7]采用基于密度和距离的方法选择初始聚类中心，进行聚类，挖掘正常模式，然后以3倍方差准则识别异常. 除此之外，YIN等[8-13]改进k-means算法，提高k-means算法全局搜索能力，提高异常检测的准确性，但其聚类过程中均以最近邻分配准则划分类别，未考虑各模式的差异性. 本研究采用上述第2类异常检测思想，提出一种新的异常检测框架，首先采用网格映射的方法压缩数据，提高异常检测模型建立效率，然后以BDk-means(border dividek-means)算法识别系统中的正常模式，为提高电力信息系统数据异常检测的精确度提供参考.

1 基于BDk-means聚类的电力信息系统异常检测方法

基于BDk-means聚类的电力信息系统异常检测方法主要分为模式挖掘和异常识别两个过程(图1).

1)模式挖掘：电力信息系统监控数据经压缩后，使用BDk-means算法对历史监控数据进行聚类，挖掘系统存在的正常模式.

2)异常识别：计算样本点与正常模式的偏离程度，将偏离程度高于阈值的样本点视为异常点.

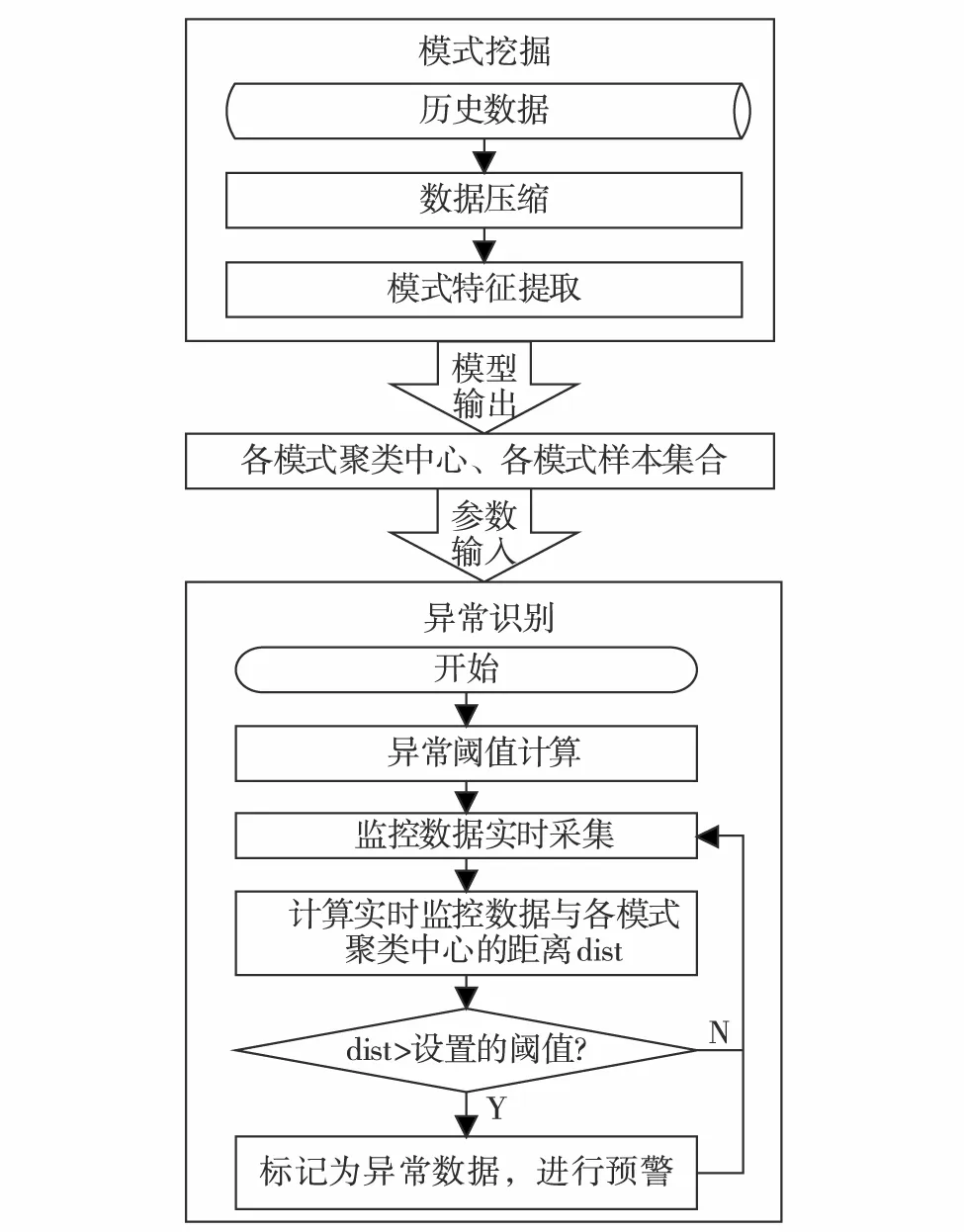
图1 异常检测框架Fig.1 Framework for anomaly detection

为便于描述本研究提出的异常检测方法，表1对参数进行了说明.

表1 参数说明

1.1 模式挖掘

模式挖掘的目的是从众多的历史数据中，识别出系统的正常模式. 由于电力信息系统单位时间采集一次数据，采集频率高、时间跨度大，具有众多相似或重复数据，在特征提取过程中将进行大量重复计算. 所以，模式挖掘过程分为数据压缩和模式特征提取两个步骤.

1.1.1 基于网格的数据压缩

考虑到数据各维度的度量存在不同数量级问题，数据压缩前，本研究基于minmax准则，将数据各维度统一规范化，如式(1).

(1)

然后，在数据空间中划分网格，以各网格内样本点的均值及其权重因子(各网格内样本点的数量)作为新的数据集合. 如图2，各网格的均值点及其权重组成的数据集{(m1,w1), (m2,w2), (m3,w3), (m4,w4)}表示压缩后的数据集. 其中，mi为regioni内样本点均值，wi为regioni内样本点数.

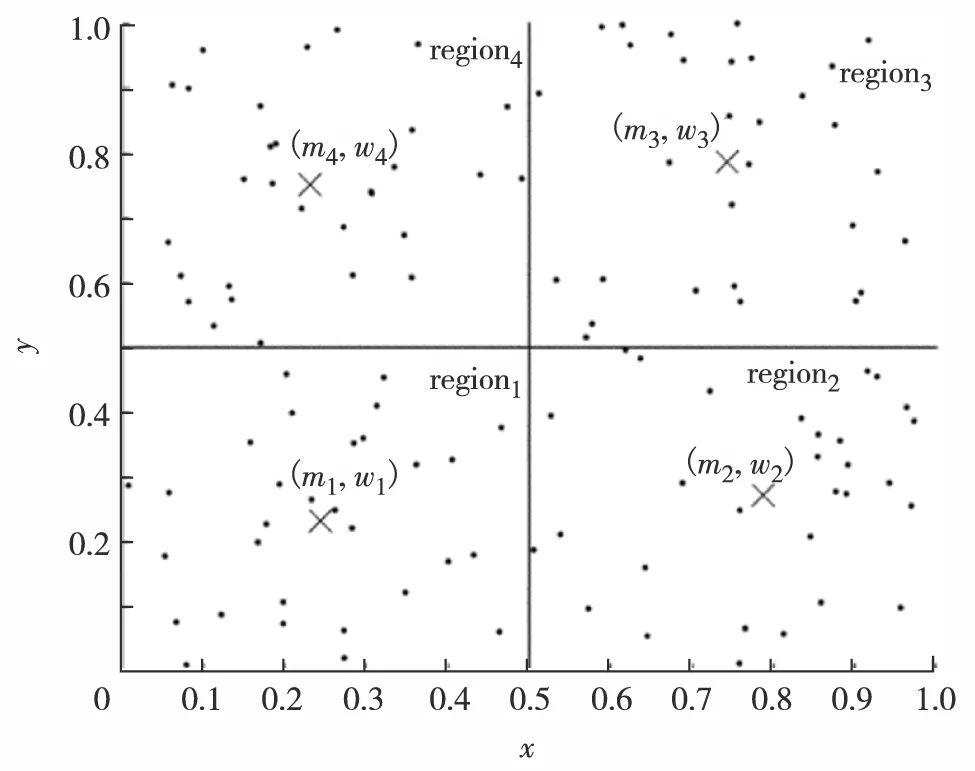
图2 数据压缩示例Fig.2 Data compression example

1.1.2 基于BDk-means的模式特征提取

BDk-means算法在传统k-means算法的基础上，引入聚类边界再分配机制(当边界密度大于簇密度时，每次迭代使聚类边界向密度小的方向移动)，使边界密度逐步向下收敛，得到边界清晰的聚类划分，准确提取正常模式，主要包含初始聚类中心选择、模式更新和聚类中心更新等3个步骤.

为便于描述本研究提出的BDk-means算法，给出以下定义.

定义1簇边界区间：给定任意两个簇i、j和边界范围参数s， 簇边界区间(edgei, j)表示处于直线L1和直线L2之间的平面空间，其中，L1(a1x+b1y+c1)和L2(a2x+b2y+c2=0)分别表示线段CiCj的垂直平分线L0前后平移s的直线，如图3.

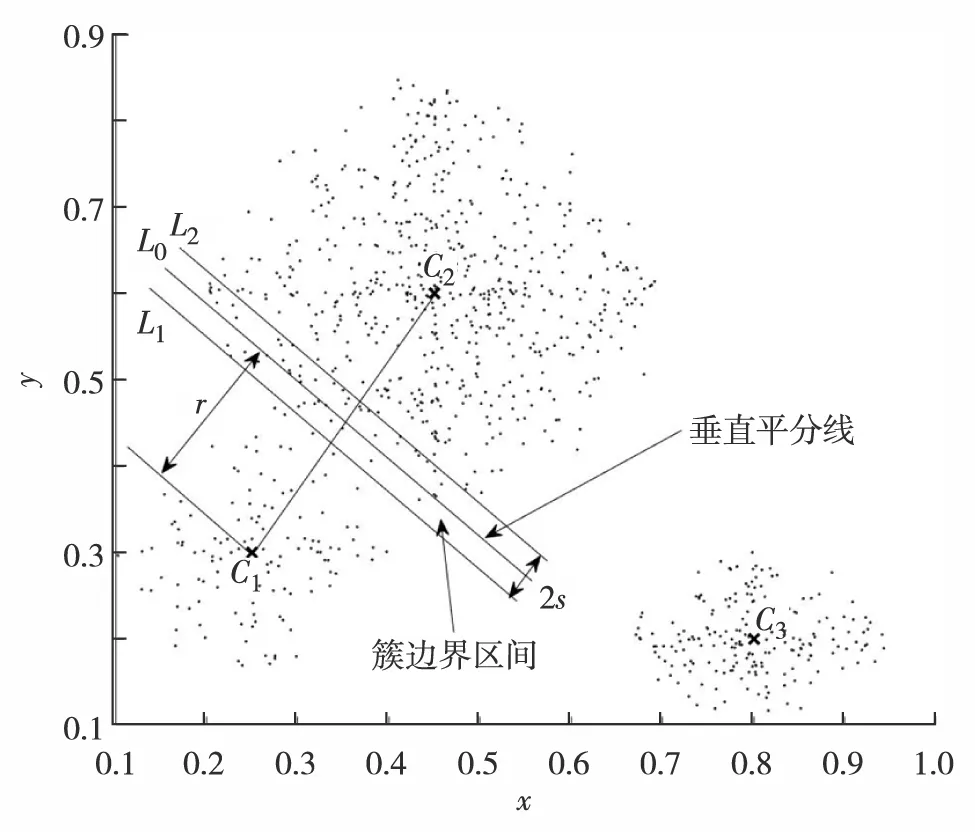
图3 边界划分示意Fig.3 Edge demarcation

定义2边界样本：给定任意两个簇i和j， 其边界样本ePointi, j表示处于平面空间edgei， j内的样本点(x,y)， 如图3中介于直线L1和直线L2之间的样本点P(x,y)， 满足约束：

(2)

1) 初始聚类中心选择

传统k-means算法初始聚类中心选择过程具有随机性，选择不同的初始聚类中心，算法陷入的局部最优解不同，可能得到不理想的局部最优解. 因此，本研究提出一种改进的初始聚类中心选择算法，首先对于给定数据集建立如图4所示的坐标空间，然后确定坐标空间中与原点距离的最大样本点maxP和最小样本点minP，并以原点为圆心将坐标空间切分为图4所示的k个等宽圆环空间，每个圆环空间Ci表示为

Ci={in_ri, out_ri}

(3)

其中， in_ri和out_ri分别代表圆环空间的外环和内环， 具体定义为

(4)

(5)

其中，dist(o, minP)和dist(o, maxP)分别表示原点o到样本点maxP和minP的距离.

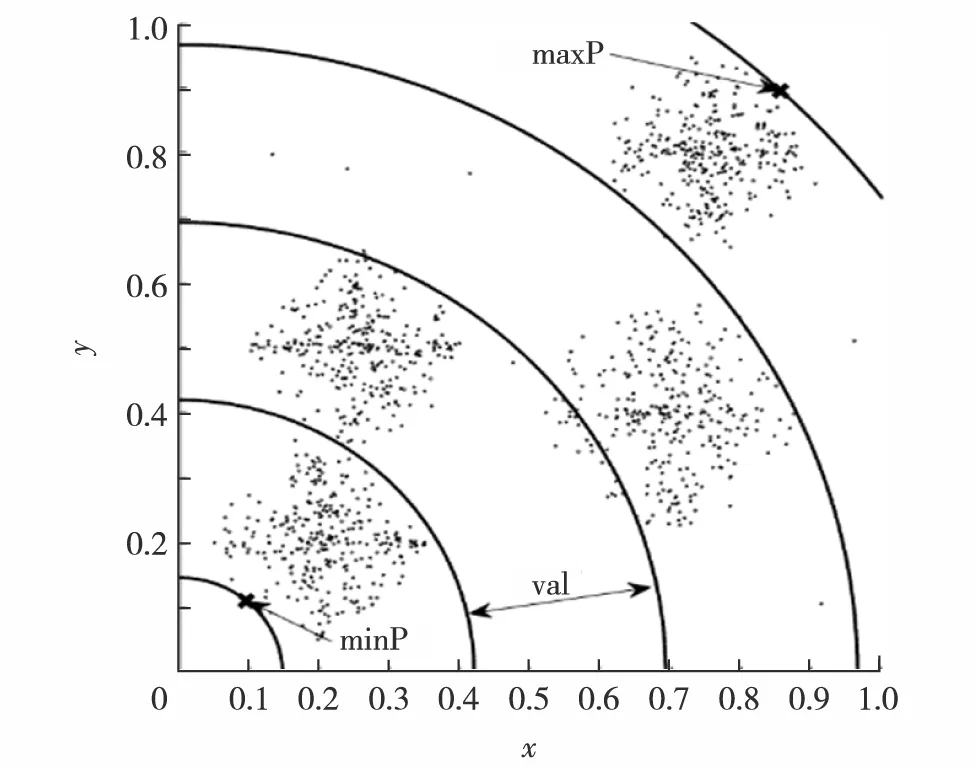
图4 初始聚类Fig.4 Initial clustering

本研究将各圆环内样本点的集合视为初始簇，并基于加权均值更新聚类中心：

(6)

(7)

其中， |Pi|为Pi集合中样本点的个数；wl为经数据压缩后样本点Pi[l]的权重.

2) 模式更新

一般来说，电力信息系统数据模式分布具有差异性(图3)，模式C1中样本离中心距离较小，模式C2中样本离中心距离较大.

传统k-means算法以最近邻准则标记样本点类别，以图3中C1C2的垂直平分线L0划分两种模式，将L0至L2中的样本点划分为模式C1， 然而L0两侧样本点分布类似，均为模式C2中的样本点. 因此，本研究提出一种边界再分配策略，首先以最近邻准则划分初始簇，分配样本点为其最近邻簇Pm，获得初步聚类划分P1,P2,P3, … ,Pk，样本点所属类别由式(8)确定：

(8)

计算每一样本点与最近邻簇心Ci和次近邻簇心Cj垂直平分线的距离，当其小于给定的边界范围s， 则视该样本点为边界edgei, j的边界样本点ePointi, j. 通过比较边界样本点密度bDensi, j与簇i、j相对聚类边界edgei, j的密度cDensi, j和cDensj, i, 当边界密度bDensi, j>cDensi, j或cDensj, i时，划分边界样本点到簇相对密度更大的簇，否则以最近邻准则标记样本点类别.

边界密度bDensi, j为

(9)

其中， |ePointi, j|为边界edgei, j样本点数量；s为给定的边界范围参数. 簇i相对聚类边界edgei, j的簇相对密度为

(10)

ri, j=dist(ci,cj)/2

(11)

其中， |Pi|表示簇i的样本点数量.

3) 聚类中心更新

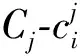
(12)

(13)

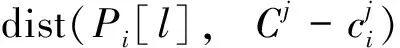
1.2 异常识别

异常识别过程基于已挖掘出电力信息系统的正常模式，通过设置各模式的异常阈值，识别异常[14]. 鉴于电力监控数据中未记录历史故障数据以及各簇分布不服从正态分布，本研究以各正常模式箱型图的上限作为异常阈值thresholdi. 根据正常模式聚类中心及各模式异常阈值进行实时数据的异常识别步骤为：

1)电力信息系统监控数据实时采集；

2)计算实时监控数据与各聚类中心的距离D_CP0, D_CP1, …, D_CPk；

3)当实时监控样本点与各正常模式中心的距离D_CPi均大于异常距离thresholdi时，则识别其为异常数据，进行异常预警.

2 实验仿真及结果

2.1 数据集及实验环境

基于BDk-means聚类的电力信息系统异常检测实验，实验数据选取某电力信息系统某一主机网络流入量和网络流出量两个维度近1年所产生的约6万条数据，实验环境为python3.6、win10 64位、主频2.3 GHz，内存8 Gbyte.

实验中将本研究提出的异常检测方法与基于传统k-means、PSO-k-means[9]和Minmax-k-means[15]聚类算法的异常检测方法相比较.

2.2 评价指标

2.2.1 模式挖掘评价指标

本实验使用聚类内部评价指标轮廓系数(SilCoe)和S_Dbwnew[16-17]评估模式挖掘的准确性.

1) 轮廓系数.以样本点为单位评估聚类的准确性，其取值在-1～1，计算公式为

(14)

其中，a表示样本点与其所属簇其他样本点的平均距离；b表示样本点与其所属簇的最近邻簇样本点的平均距离.

2) S_Dbwnew. 以簇为单位评估聚类的准确性，其取值为0到正无穷，计算公式为

S_Dbwnew=Dens_bwnew+Scatnew

(15)

其中， Dens_bwnew为聚类边缘密度与数据簇心密度之比；Scatnew为簇标准差与数据空间整体标准差之比.

通常，轮廓系数越接近1， S_Dbwnew越小，表明挖掘的模式越准确.

2.2.2 异常识别评价指标

本研究提出异常距离(abnormal distance, AbnDst)评估异常检测结果的有效性，计算公式为

(16)

其中， dist(AP,P)表示异常样本点AP至正常样本点P的距离， |AbnS|表示异常数据集AbnS中元素的数量. 一般来说，异常距离大小与异常可能性成正相关.

2.3 实验结果

异常检测算法对比实验统一采用未压缩的数据，将本研究所提方法与其他3种方法相比较，以保证对比实验的可靠性. 首先，对比4种算法的聚类图，不同类别的样本点在图中以不同的灰度显示，如图5.

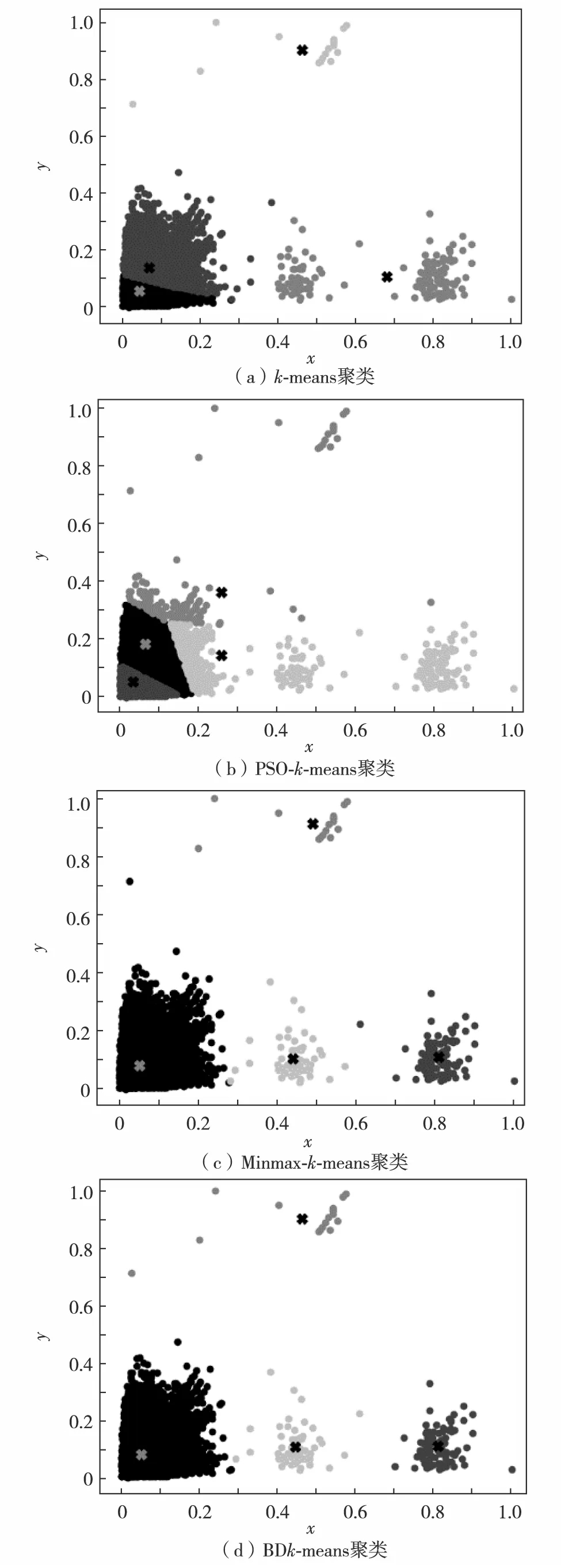
图5 聚类结果对比Fig.5 Comparison of cluster results

传统k-means及PSO-k-means算法的各模式边界处样本点数量较多，说明该部分样本点属于两种模式的可能性相似，无法准确确认其所属模式. 而Minmax-k-means与本研究提出的BDk-means挖掘的各模式边界处样本点数量更少，模式区分更加明显，挖掘的模式准确率更高.

为进一步验证BDk-means算法的有效性，对比基于BDk-means和Minmax-k-means异常检测的各指标值，如表2.

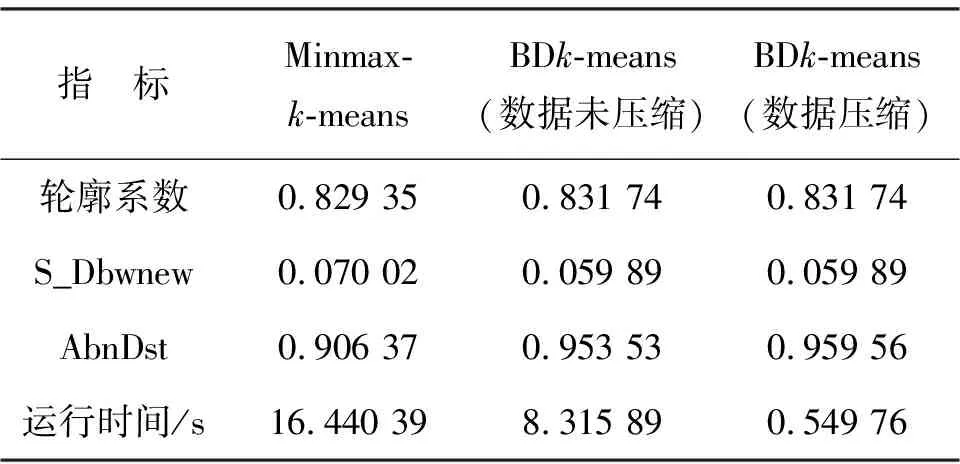
表2 算法性能对比

BDk-means算法比Minmax-k-means算法聚类结果的轮廓系数更接近1，具有更小的S_Dbwnew和更大的异常距离. 另外，BDk-means算法运行时间为Minmax-k-means执行时间的50%，原因是Minmax-k-means算法每次迭代均需先后两次对每一样本点进行类别划分，第1次计算各类别的权重，第2次确定模式，而本研究算法第2次仅需对边界处样本点统一划分模式，使得模式挖掘效率有明显提升.

考虑到电力信息系统数据的特色，增加数据压缩步骤后，异常检测模型的运行时间由8.32 s降低至0.55 s，进一步提高了效率，且各指标基本保持不变. 可见，本研究提出的数据压缩方法能有效提高异常检测效率.

综上，本研究提出的基于BDk-means聚类的异常检测方法对电力信息系统的异常检测具有一定参考价值.

结 语

提出一种基于BDk-means聚类的异常检测方法. 该方法基于网格映射进行数据压缩，有效提高了异常检测效率，并改进k-means算法，解决了传统k-means算法聚类中心敏感、无法准确挖掘分布差异过大模式的问题. 实验结果表明，与现有算法相比，本研究异常检测方法在准确度及效率方面有了较大提升，对电力信息系统的异常检测具有重要的指导意义.