基于REICH模型的同高度交叉航路碰撞风险研究
2020-03-18刘章
刘 章
深圳航空有限责任公司,广东深圳 518128
近年来随着国民经济快速稳定发展和人民收入水平不断提升,中国民航业得以飞速发展.运输总周转量逐年上升,且增长幅度远高于其他运输方式[1].不断增长的航空需求与受限的民用空域资源间的矛盾日益凸显,航线冲突率与航班延误率日趋严重.因此,合理提高空域利用率具有重要意义.
在有限空域资源条件下,安全科学地优化航路交通流被认为是一种提高空域利用率的有效途径[2].航路交通流优化着眼于在局部范围内确定航空器的安全距离,避免航空器之间以及航空器与障碍物发生碰撞.已有研究多以相应安全标准为目标,研究如何通过缩小纵向、侧向及垂直间隔,提升航路容量和航路利用率[3].HSU[4]首次提出碰撞临界区的概念,并运用概率论方法构建交叉航路的碰撞风险模型.王艳军[5]结合航空器及空域运行特征,将交通堵塞传播终止条件引入空中交通拉格朗日模型,对航路及区域容量进行估算.张兆宁等[6]考虑管制员、飞行员及导航设备因素,利用随机微分方程并结合停滞时间和特定分类事件构建碰撞风险评估模型.此外,REICH[7]通过构建REICH模型针对大西洋区平行航路上,由技术误差、系统误差及导航误差构成的飞行误差所引起的侧向、纵向及垂直方向的碰撞风险进行研究,REICH模型基本结构如图1,其基本原理是把飞机A模拟成一个矩形碰撞盒,并在飞机A周围设计一个临近层,当飞机B进入临近层时,A与B就存在侧向、纵向及垂直方向的碰撞风险;当B进入矩形碰撞盒时,两者将发生碰撞,通过分析碰撞率和碰撞次数可对碰撞风险进行评估.图1中,λx、λy和λz分别为飞机A机身的长、宽和高;Sx、Sy和Sz分别为碰撞盒纵向、侧向及垂直间隔标准.
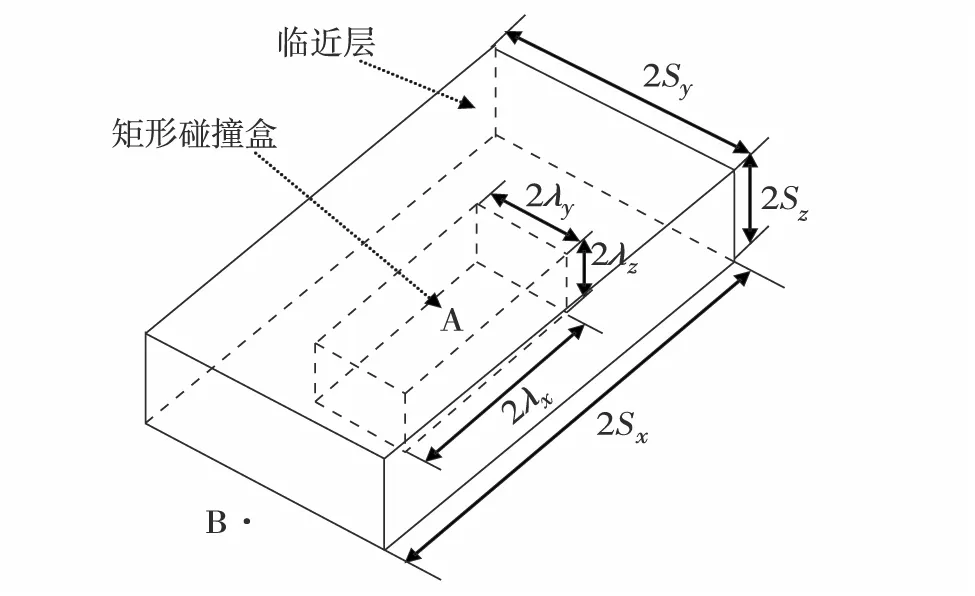
图1 REICH模型基本结构图[7]Fig.1 Schematic diagram of REICH model[7]
REICH模型具有较强的可拓展性,至今已得到不断发展及完善.从理论优化和工程实践的综合角度来看,近年来该模型的应用主要集中于飞机进近着陆风险分析[8]、平行跑道碰撞风险计算[9]以及尾流间隔标准影响评估[10]等方面.由于REICH模型应用条件涉及航空器较多的性能和运营参数,加之对于同高度交叉航路上碰撞风险的计算较为复杂,鲜有研究利用该模型对提高同高度航路空间利用率和缓解航班延误等问题进行分析.本研究基于REICH模型对同高度交叉航路上侧向间隔的安全性进行评估,提出可用于分析交叉航路碰撞风险的计算方法,结合中国民航实例数据,实践并验证该方法有效,以期为民航运营管制部门在优化航路交通流和提高空间利用率方面提供有效决策参考依据.
1 同高度交叉航路碰撞风险计算方法
同高度交叉航路碰撞风险计算方法的目标是通过科学计算交叉航路上飞机碰撞风险,提供合理的航路安全性参考,使处于交叉航路上的飞机可以使用同一高度,有效提高空间利用率、增加航线密度并优化航路流量控制.同高度交叉航路构型如图2.其中,L1、L3和L4为同高度平行航路;L2为与前三者同高度交叉的航路;L1与L2的夹角为β; 飞机A与飞机B在后者航路直线上的纵向间隔为Sx;DB为飞机B标称位置的瞬时侧向位置误差,其长度|DB|≤Sy, 且∠DBE=β.
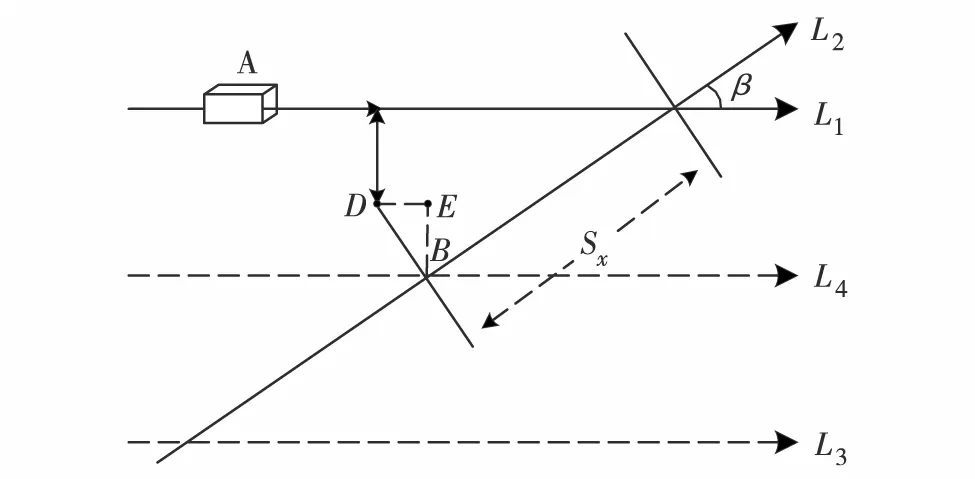
图2 同高度交叉航路构型示意图Fig.2 Illustration for crossing airlines at the same altitude
1.1 假设条件
该方法的主体构型基于REICH模型,其参数设置及假设条件如下:
1) 模型针对同高度2条交叉航路上2架飞机的碰撞风险进行研究,不考虑≥3条航路或3架飞机的情形.
2) 飞机在无故障及不受恶劣天气影响情况下保持航路,以相对稳定的高度和速度在静风条件下飞行.
3)u、v及w分别是飞机A和B在纵向、侧向及垂直方向的相对速度;2λx、 2λy和2λz分别是矩形碰撞盒的长、宽和高.
4) 飞机A和B的相对位置彼此独立,且A和B自身在纵向、侧向及垂直方向上的位置相互独立,碰撞盒垂直间隔标准Sz=0.
1.2 碰撞风险分析
由于飞机A和B在纵向、侧向及垂直方向的位置相互独立,并且两机的位置相互独立,则飞机B在单位小时内沿纵向、侧向及垂直方向进入飞机A临近层所导致的碰撞次数分别为NxPyPz、NzPxPy及NyPxPz, 因此,单位临近时间的碰撞次数为
CR=NxPyPz+NyPxPz+NzPxPy
(1)
因为
(2)
所以
CR=NxPyPz+NyPxPz+NzPxPy=
(3)
其中,CR为单位临近时间内飞机B进入飞机A矩形碰撞盒的次数;Nx、Ny及Nz为飞机A和B纵向、侧向及垂直间隔小于λx、λy及λz的频率,且λx、λy及λz分别为飞机B穿越临近层单位时间内的纵向、侧向及垂直方向的碰撞次数;Px、Py及Pz表示飞机B进入飞机A矩形碰撞盒的概率,即两机之间出现纵向、侧向及垂直方向重叠的概率,其值分别为飞机B纵向、侧向及垂直方向穿越矩形碰撞盒时间与穿越临近层时间的比值;tx、ty及tz分别表示飞机B纵向、侧向及垂直方向穿越飞机A矩形碰撞盒的时间,
tx=2λx/u,ty=2λy/v,tz=2λz/w
(4)
因此
Px(Sx)Py(Sy)Pz(Sz)
(5)
由于本研究是关于同高度交叉航路碰撞风险,
Sz=0
(6-a)
Pz(Sz)=Pz(0)
(6-b)
则由式(5)、式(6-a)和式(6-b)可得到同高度交叉航路碰撞风险为
CR=Px(Sx)Py(Sy)Pz(0)
(7)
2 参数确定
式(7)的计算涉及航路侧向、纵向和垂直重叠概率以及相应的飞机相对速度,其中,侧向、纵向及垂直3个方向的重叠概率均可应用概率分布方法推导获得.飞机相对速度受技术运行和实测条件制约,其精确数值往往较难直接获得,因此,应用模糊方法对相应测量数据进行处理,以获得置信度较高的数值.
2.1 侧向重叠概率
交叉航路侧向重叠的特点是相对平行航路而言,先计算平行航路的侧向重叠概率.平行航路中侧向间隔Sy保持固定不变,假定飞机在飞行过程中的侧向位置误差fy(y1)服从混合双参数指数分布[7]
(8)
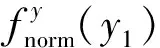
(9)
(10)
其中,a1和a2分别为一般导航误差和严重导航误差的概率密度函数参数.由前文假设条件可知,飞机在纵向、侧向及垂直方向上的位置分量相互独立,并且两机之间的位置也彼此相互独立,因此,在平行航路相同高度层上两机发生侧向重叠的概率为
(11)
相比于平行航路,交叉航路的侧向间隔标准Sy随着飞机的持续飞行而发生改变,飞机间的侧向重叠概率Py(Sy)也随之发生改变,因此,侧向碰撞风险也在不断变化.由图2可知,Sy的变化范围为[0,Sxsinβ]; 飞机A和B之间的侧向重叠概率可以看作矩形碰撞盒A和质点B所在虚拟平行航路的侧向重叠概率,且|BE|=|BD|×cosβ. 由于两飞机A和B位置相互独立,则A和B侧向重叠概率为

(12)
由于飞机侧向重叠概率不断改变,可计算A和B在同高度交叉航路上侧向重叠概率的平均值为
Py(Sy)≈
(13)
2.2 纵向重叠概率
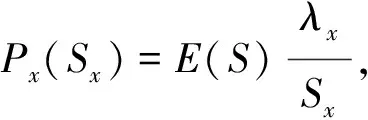
(14)
2.3 垂直重叠概率
垂直间隔是指同航迹相邻高度层的两飞机之间的垂直高度差,其影响因素主要有技术误差和运行误差.技术误差指飞机在特定高度层上飞行产生的误差,包括高度测量系统误差和高度保持误差;运行误差是由于计量单位差异、飞机设备老化等原因导致的指令高度与实际高度之间的误差.高度测量系统误差(altimeter system error, ASE)与该飞机的高度系统显示精确度相关,而高度保持误差(altitude assigned deviation, AAD)与飞行空域环境直接相关,可假定飞机垂直方向高度测量系统误差和高度保持误差分别服从指数分布和双参数指数分布[11].
高度测量系统误差的概率密度函数为
(15)
高度保持误差的概率密度函数为
(16)
其中,ρ为高度测量系统误差概率密度函数的参数;σ为在飞机在非正常情况运行下,高度保持误差所占的比例;b1和b2分别表示在飞机运行正常和非正常情况下,飞机高度保持误差的概率密度函数中参数.该空域范围内所有飞机的高度测量系统误差为
(17)
其中,ηi表示第i种机型所占比例;fiASE(Z′)为第i种机型高度测量系统误差的概率密度函数.假设高度测量系统误差与高度保持误差相互独立,则技术误差概率密度函数为

(18)
两飞机在纵向、侧向及垂直方向上的位置相互独立,且飞机间的位置彼此也相互独立,则在同航迹同高度层上由于技术误差引起垂直重叠的概率可通过卷积积分公式计得,

(19)
2.4 飞机相对速度值
飞机相对速度值与两架飞机的动态航行特点同时相关,并受时限条件和技术手段等制约,获得直接的精确数值难度较大,可采用模糊方法对基本数据处理得到较为准确的实际数据[12],流程如下.
步骤1构建模糊分析矩阵H.飞机相对速度集合V={u,v,w}, 采集数据共J组,构建矩阵H
(20)
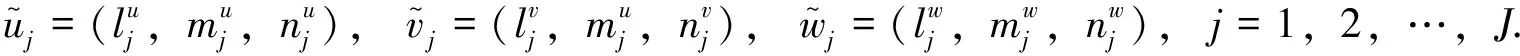
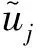
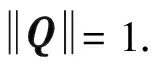
综合以上分析,可得同高度交叉航路飞机碰撞风险为
CR=Px(Sx)Py(Sy)Pz(0)
(21)
3 实例分析
图3为京广A461航线与成沪B213航线实例示意图.A461航线(正北基准偏纵向)和B213航线(正北基准偏横向)交点位于中国武汉地区上空,交叉角约为60°.
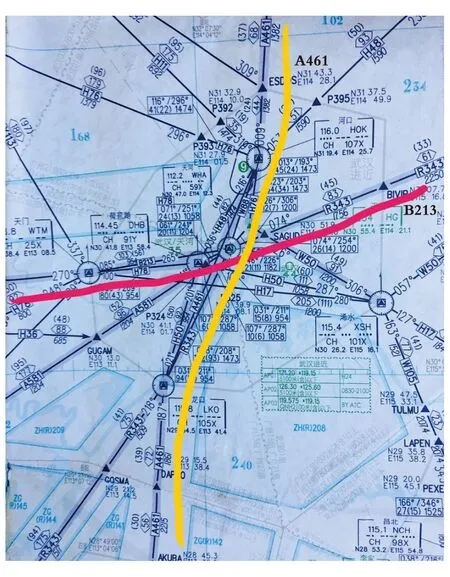
图3 A461航线与B213航线实例示意图Fig.3 (Color online) Illustration of A461 and B213
3.1 矩形碰撞盒参数
该空域内飞行的各机型机身长、翼展、机身高及飞行时间比例如表1,计算加权平均值可得λx、λy及λz,进而求得2λx、 2λy及2λz分别为109.18、98.46及31.74 m.
3.2 侧向重叠参数
侧向误差中导航误差概率密度函数参数a1和a2均与相应区域导航性能精度值RNP密切相关[13],
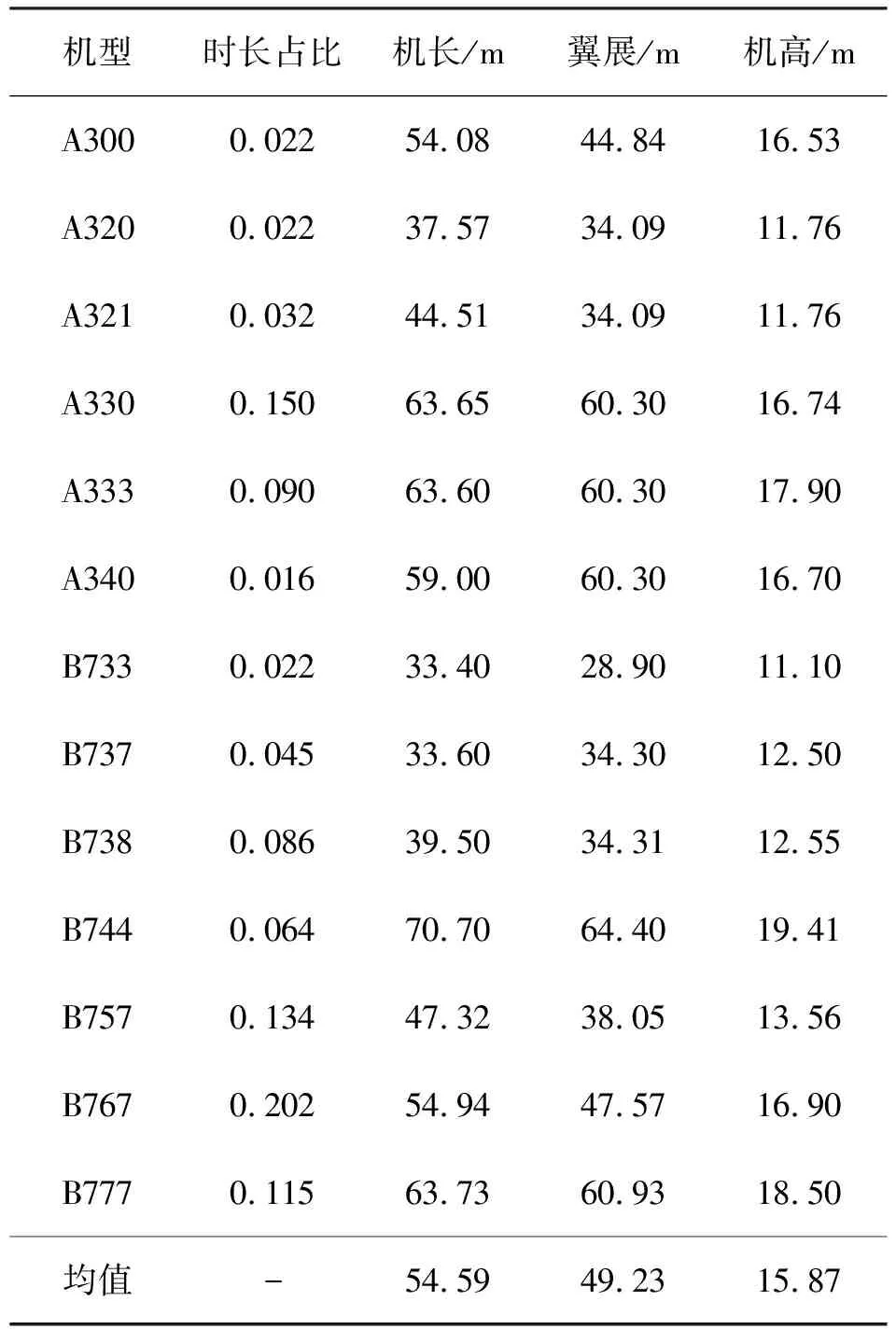
表1 各机型飞行参数
当RNP=n时,
(22)
因此,
(23)
当n=1时,a1=0.33 m;n=4时,a1=1.33 m;n=10时,a1=3.33 m.选取典型的n=4时的情况分析,则a2=16 m,对应出现严重误差的比例δ=2.995 7×10-5海里=0.055 m[13].
3.3 纵向重叠参数
纵向间隔一般分程序管制和雷达管制,本研究只考虑雷达管制情形,根据中华人民共和国国务院和中央军委空中交通管制委员会关于空中飞行间隔的规定[13],在相同高度航路交叉且相应交叉夹角β<90°的情况下,纵向间隔标准Sx=40 km.由图3可知,武汉上空两航路夹角近似60°,故此处取β=60°,E(S)=0.01[11].
3.4 垂直重叠参数
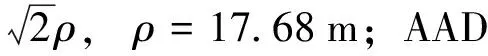
3.5 飞机相对速度
两航路交叉区域飞机之间在纵向、侧向及垂直方向上相对飞行速度u,v及w的5组测量统计数据如表2.为简化计算,取模糊截集水平α=0.5, 相应数据权重矩阵Q=[0.2, 0.2, 0.2, 0.2, 0.2]T, 进一步计算得u=21、v=42及w=1.5节.

表2 飞机相对速度测量统计数据
实例中交叉航路碰撞风险计算的相关参数汇总如表3,由式(21)得CR=3.581 3×10-10,国际民航组织规定安全侧向间隔条件对应的目标风险等级为5×10-9[5],满足规定的侧向间隔安全等级标准,因此,本研究提出的基于REICH模型的同高度交叉航路碰撞风险计算方法可行.
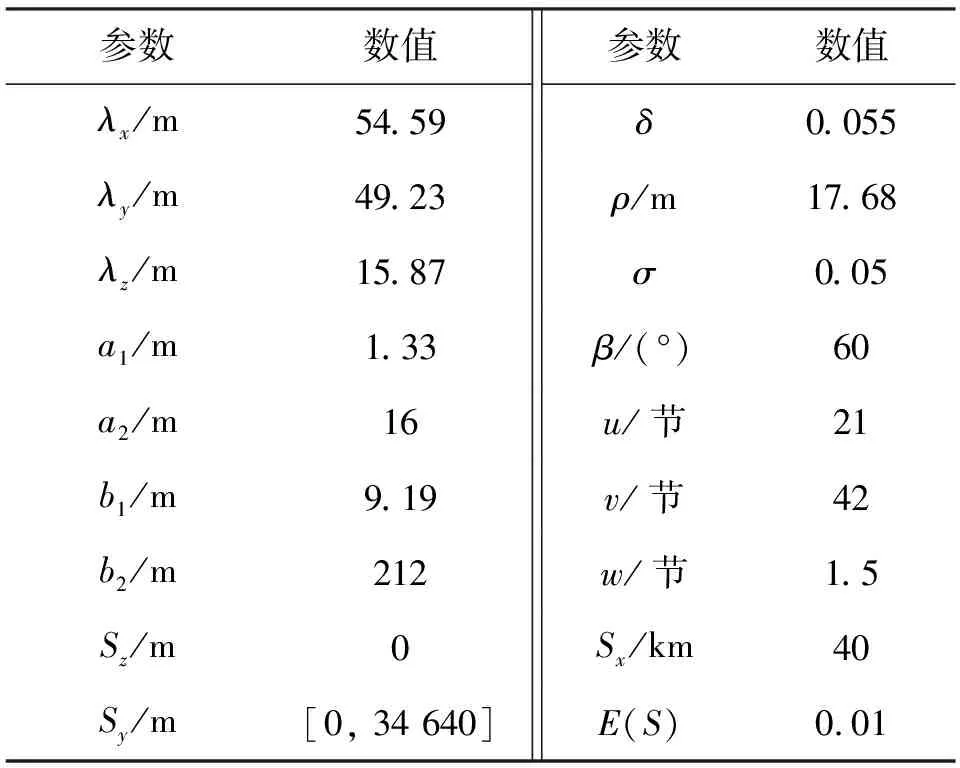
表3 实例计算参数汇总表
结 语
本研究以实际航空运营中航路交通流安全与优化问题为切入点,基于REICH 模型分析同高度交叉航路构型,运用概率论等知识对飞机碰撞风险进行深入研究,实例计算结果验证将基于REICH模型的碰撞风险分析方法用于同高度交叉航路有效可行,为进一步确定最小航路安全间隔提供一种新的有效途径.由于缺乏全面的航路密度统计数据,且没有考虑天气变量和人为反应时间误差等情况,该方法虽然给出了策略性分析和方法论证,但尚未实现对全高度层航路流量控制情况的模拟仿真检验,以验证其对于缓解流量控制的有效程度,待所需统计数据补充完善后可进行进一步仿真验证.
