冻土导热系数骨架模型研究
2020-03-18李顺群王彦洋夏锦红陈之祥
李顺群,张 翻,王彦洋,夏锦红,陈之祥
1)天津城建大学土木工程学院,天津 300384;2)天津市软土特性与工程环境重点实验室,天津 300384;3)天津市建设工程技术研究所,天津 300204;4)新乡学院土木工程与建筑学院,河南新乡 453003;5)大连理工大学工业装备结构分析国家重点实验室,辽宁大连 116085
导热系数是寒区水工结构物温度场预测以及进行冻胀融沉量评估的重要参数.受矿物成分、含水量、密度和含冰量等多种因素影响,多孔、多相、碎散的岩土材料的导热系数变化将变得更为复杂.因此,准确计算多种因素作用下岩土的导热系数,对于温度场预测、冻结温度场模型试验以及热方程的解析求解具有重要意义[1-4].
相体含量、温度和干密度等条件是冻土导热系数的重要因素,据此建立了考虑土、水和冰三相体积含量的饱和冻土导热系数预估模型,即几何平均法[5];基于归一化方法建立了考虑饱和度影响的非饱和(冻)土导热系数预估模型[6].除上述研究之外,众多研究人员对冻土导热系数的影响因素展开相应的研究,并取得一定的成果[7-8].除了冻土中各物质含量及温度等条件是影响导热系数变化的主要因素外,导热系数变化还取决于冻土孔隙的分布形式.
冻土是一种各向异性的导热体,即冻土在空间中任意一点的导热能力都是各向异性的.但是,点的概念不能涵盖土颗粒、孔隙冰和孔隙水的含量关系,因此引入空间代表体元(representative elementary volume, REV)的概念[9],即空间中任意点的空间体积代表体,以此解释冻土在空间中组成物质含量的连续性.引入REV概念既可以保证冻土物质含量在空间中的连续性,同时也能保证空间中冻土导热的连续性.在保证冻土在空间中传热的连续性基础上,基于REV概念,假设冻土在空间中的传热为各向同性.
本研究假设土颗粒为均质的球缺球体(图1),且土颗粒彼此间为等效球缺接触,以此建立密实与非密实排列的两种土骨架模型及土水冰之间的复合传热模式,并根据建立的骨架几何模型与复合传热模式,推导出饱和冻土导热系数的预估模型.
1 土体球缺接触
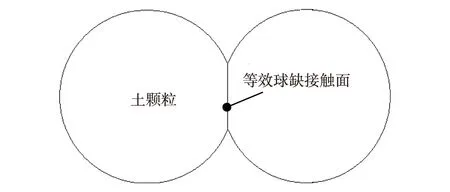
图1 等效球缺接触Fig.1 Equivalent ball missing contact
土颗粒在形成过程中,在受到风、水以及重力等外部因素主导的搬运冲刷作用下,土颗粒被磨圆成近似球体以及椭圆体[10-11].为了方便研究,将土颗粒假设成均匀球体.实际上,土颗粒间存在诸如点接触和面接触等多种接触方式,故假设土颗粒间接触等效为球缺接触, 如图1. 由图1可见, 球缺接触的土颗粒体积Vs要小于等直径球体的体积Vq,即
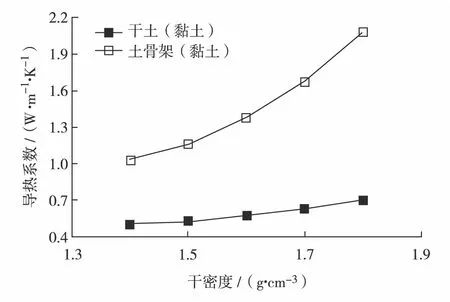
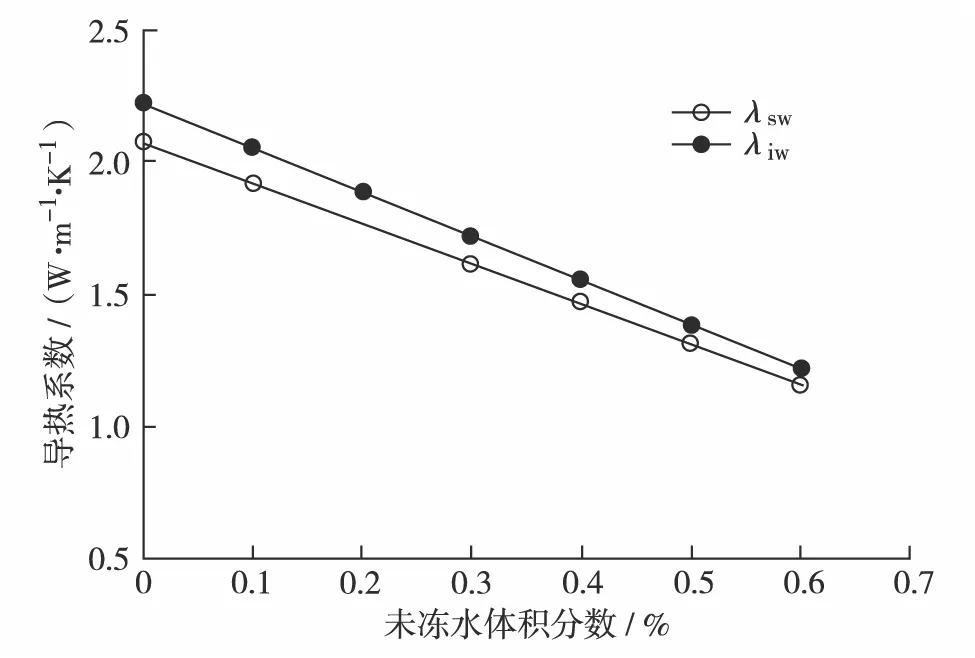
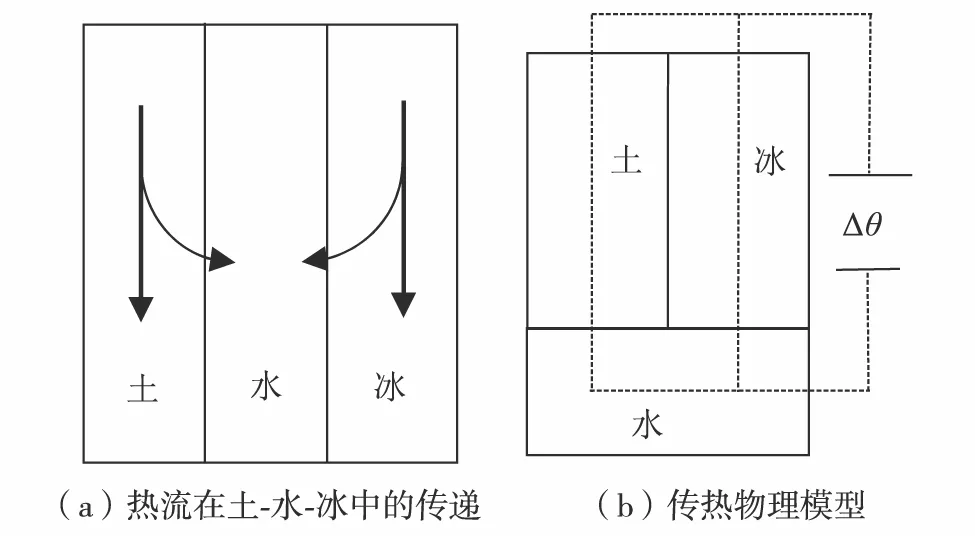
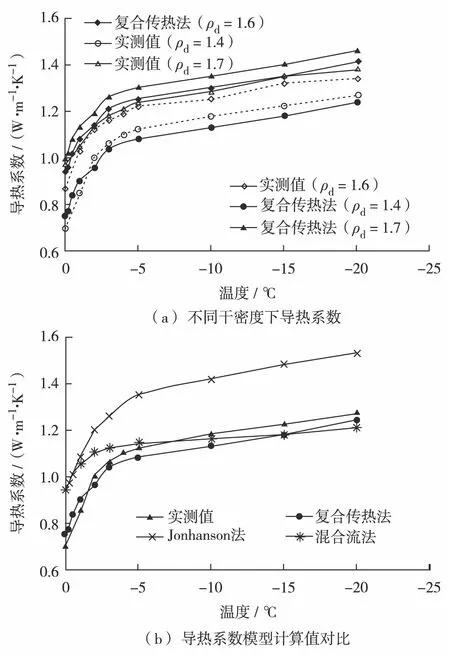
Vs (1) 欲求得Vs,须求得球缺部分体积V′.球缺部分为圆弧体,球缺土颗粒与球缺部分的几何关系如图2. 图2 球缺部分与球体之间的几何关系Fig.2 Geometric relationship between the missing part of the ball and the sphere 图2中存在如下关系: x2+l2=R2 (2) R-l=l′ (3) 其中,R为土颗粒半径;x为球缺部分截面半径;l′、l分别为球缺部分顶点和土颗粒中心点至球缺截面的距离.有 V′=πl′2(R-l′/3) (4) x与R的关系为 (5) 其中,a为常数,且a>1. 将式(2)、式(3)和式(5)代入式(4)并化简得 (6) 式(6)为1个球缺体积,就土体整体而言,土体中存在a′个球缺体,总的球缺体积为 V″=a′V′ (7) 其中,a′为不同排列方式下的土颗粒接触点个数. 根据土颗粒排列时的相对位置关系,可构建两个不同排列形式的土体骨架模型.一种为土颗粒正交排列的土骨架模型,另一种为土颗粒聚合密实排列的土骨架模型. 该土骨架由相同排列方式的土颗粒层竖向叠加而成.每1个土颗粒与6个土颗粒接触,每1个球形土颗粒缺少6个球缺体,如图3. 图3 正交排列土骨架Fig.3 The soil skeleton in an orthogonal pattern 如图3(b)所示,球缺土颗粒可单独占据1个边长为l1的正方体,且l1=2R-2l′. 这种排列方式下的土骨架在空间中关于xoy、yoz和zox平面对称.假设土颗粒组成一致,则该土骨架排列形式下的土体为各向同性. 空间中任意土颗粒与其他土颗粒聚合成为正四面体时,土骨架能达到相对密实状态.相比正交排列的土骨架,聚合密实排列的土骨架更为密实,孔隙体积更小,同样将该土骨架视为各向同性体.聚合密实排列的土骨架如图4. 图4 聚合密实排列的土骨架Fig.4 Aggregate compact arrangement of soil skeletons 如图4(b),密实状态下的土颗粒聚合成边长为l2的正四面体,聚合正四面体中缺少12ζ/180个球缺体,ζ为正四面体二面角,约为70°32′. 根据图3(b)以及图4(b),可计算不同排列形式土骨架所占土体体积含量.正交排列土骨架体积分数φs1为 (8) (9) 化简为 (10) 其中,Vs1为土骨架体积;V1为图3(b)所示的立方体体积. 图4(b)中土颗粒约为1/3球,根据式(8)可类比计算出聚合密实排列土骨架体积分数φs2为 (11) l2=l1 (12) 整理得 (13) 其中,ζ为正四面体二面角,约为70°32′.式(10)与式(13)中a值存在最优解,根据0<φs<1的限定条件,可得出式(10)和式(13)中a的取值范围(两式a的取值相互独立).除此之外,根据计算干土的目标孔隙率不同,a的取值也发生变化,式(10)中a>1.70, 式(13)中2.64 当式(10)中a趋于无穷大时,φs1收敛于0.52.式(13)中a为4.30时,土体为完全岩体.根据a的取值不同,可以模拟不同孔隙率土体的空间结构,进而计算出土体导热系数. 实际冻结过程,距离相邻土颗粒的球心最远端处的孔隙水最先冻结成孔隙冰.随着冻结温度的降低,孔隙冰体积含量逐渐增大并发展成为贯通的冰骨架.冰骨架具有空间整体性,但是受土颗粒排列方式的影响,正交排列土骨架中冰骨架的空间结构更具有整体性.细颗粒土体中,在温度<0 ℃条件下,土体中存在未冻水,且未冻水广泛存在于土骨架与冰骨架之间.根据水冰含量转化关系,可以计算出未冻水与孔隙冰的体积分数分别为 (14) φi=1-φs-φu (15) 其中,mu和ms分别为未冻水和土颗粒的质量(单位g);ρd和ρw分别为冻土的干密度和未冻水的密度(单位:g/cm3);wu为未冻水含量;φu和φi分别为未冻水和孔隙冰的体积分数.在土体冻结过程中,土体中将产生水分的迁移[12],即当考虑水分迁移影响时,冻土内部的水冰发生重新分布,为了简化计算,可不考虑土体冻胀效应. 冻土中各物质的体积分数可通过式(10)、式(13)、式(14)和式(15)计算获得. 未冻水含量可通过核磁共振法与混合量热法测得,对于一般土工热计算,可采用经验公式计算获得[13-15]. 冻土是多相介质组成的混合体,通过测试可以获得冻土热参数值,而且任何实测数值的验证对比均需要合理的计算公式.对冻土各组成物质热参数及其含量之间的联系,可通过数学经验公式计算得到[4].冻土各组成物质的混合导热系数λ为 (16) 其中,λi为冻土中各物质的导热系数;N为各组成物质的数量. 类比电晶格框架,得出基于冻土热传递的平层热流的导热系数表达式为 (17) JOHANSEN等[5]根据冻土中各物质的体积分数,建立了饱和及非饱和冻土的导热系数计算模型.该计算模型综合考虑了冻土中各组成物质含量的影响,但是却忽视了土颗粒排列方式及冻土中孔隙分布对导热系数的影响.根据Wiener理论模型,多孔介质在平行传热与垂直传热的不同传热模式下,多孔介质的导热系数存在两种不同计算方式.李顺群等[16]提出了混合传热模式下的冻土导热系数计算模型. 建立本研究导热系数计算模型的关键问题,就是要证明冻土的土-水和冰-水之间的传热是独立的.根据SASS等[17]的研究,当土体内部各相体导热系数相差较小时,可采用几何平均法计算土体导热系数.因此欲证明独立,只需证明土-水混合物的导热系数和冰-水混合物的导热系数在数值上相近,因此需要获得土骨架、冰骨架和未冻水的导热系数.冰和水是均质物质,导热系数已知.但土骨架是由土颗粒聚合而成的复杂聚合物,导热系数较难确定,可通过试验及计算得到. 干土是由土和气组成的二相体,且干土的导热系数受温度影响很小,可视为定值.类比孔隙水在非饱和土体中的渗流,热流在干土中会存在一个实际的传热路径.同一土样中,干土导热截面面积与其土骨架导热截面面积有如下关系: ΔF1=(1-n)ΔF2 (18) 其中,ΔF1和ΔF2分别为土骨架和干土试样的导热截面面积;n为干土试样的孔隙率. 根据导热系数测试理论公式[15]和式(18),可确定干土骨架的导热系数,即 (19) 其中,Q为热量; Δθ/Δh为温度梯度;t为时间;λdry为干土的导热系数. 根据文献[7]中的干土导热系数数据,利用式(19)可以求得不同干密度下的土骨架导热系数,如图5所示. 图5 不同干密度下干土和土骨架的导热系数Fig.5 Thermal conductivity of dry soil and the soil skeleton under different dry densities 由图5可见,干密度为1.8 g/cm3时土骨架的导热系数值为2.07 W/(m·K),冰的导热系数取值为2.22 W/(m·K),未冻水的导热系数取值为0.55 W/(m·K).根据式(16)可以计算出土-水混合物和冰水混合物的导热系数,即 λsw=λsφs+λwφu (20) λrw=λiφi+λwφu (21) φs=φi (22) 其中,λsw和λiw分别为土水混合物和冰-水混合物的导热系数.式(20)和式(21)的计算结果如图6. 图6 土水混合物和冰水混合物的导热系数Fig.6 Thermal conductivity coefficient of soil-water mixture and ice-water mixture 从图6可见,当组成物的体积分数相同时,土水混合物和冰水混合物的导热系数在数值上相差较小,表示土水混合物和冰水混合物的导热能力相近,可看作两种混合物独立传热. 图7 传热模式和传热物理模型Fig.7 Heat transfer mode and its physical model 土骨架的导热系数与孔隙冰的导热系数相差不过一个数量级,可视为热流在土骨架与孔隙冰中为独立传递,而土骨架与孔隙水、孔隙冰与孔隙水之间为混合传热,构成的土水、冰水之间的传热利用几何平均法计算.基于上述假设,提出土、水和冰组合形式下复合热传递模型.冻土中热传递如图7(a).类比电流在电晶格中传递,复合传热模型如图7(b).基于式(16)和式(17),可推导出复合传热计算模型: 1)当冻土中热主要以土、水和冰、水路径进行传递时,冻土的导热系数分为两部分.土、水间热传递为 (23) 冰-水间热传递为 (24) 2)考虑冻土中土-水与冰-水间的平行传热,则冻土导热系数计算式为 λ=λ1φ1+λ2φ2 (25) 将式(23)和式(24)代入式(25)中,可得 (26) 其中,λs,λw和λi分别为土骨架、未冻水和孔隙冰的导热系数.将式(10)、式(13)、式(14)和式(15)代入式(26),可得到冻土导热系数计算式. 实际上,冻土冻结过程可分成冰核形成与冰骨架形成两个阶段,这两个阶段的传热形式有所不同.冰核形成阶段,冰核存在于孔隙水中,此过程主要为土水之间传热;冰骨架形成阶段,冻土中冰核发展成完整孔隙冰骨架,此过程主要为土-水-冰之间传热. 基于瞬态平面热源法测试冻土导热系数,试验配制干密度分别为1.4、1.6和1.7 g/cm3的饱和粉土试样,并在低温箱的不同温度环境冷冻48 h以上,制成饱和冻土试样.将冻土试样平滑切成等大的两部分,并将测试探头放置于切割面上且加紧探头.将加紧探头的冻土试样放入恒温箱中,待探头温度与试样温度一致时开始测试.单个试样的测试时间控制在5 min左右.测试发现,干粉土试样导热系数随温度变化幅度很小,可以认为干粉土导热系数在不同温度下为一个定值. 根据给定的干密度值可以确定干土试样孔隙率.结合a值,基于土颗粒的两种排列方式,可以拟算出不同干密度下冻土试样的导热系数,如图8(a).将复合传热法与Johansen法、混合流法、实测值进行数值比对,结果如图8(b). 图8 复合传热模型计算值Fig.8 Calculation value of composite heat transfer model 如图8(a)所示,利用复合传热法计算出3种干密度情况下的导热系数值,实测导热系数值均落在计算值区间内.从图8(a)可见,在温度区间-5~0 ℃ 时,计算值大于实测值,这是由于冻结开始时,冻土内部开始形成冻结的冰核,但是冰核并未发展成为贯通的骨架体系,故导致计算值大于实测值.除此之外,冻结过程中的水热迁移也是导致实测值小于计算值的重要因素.干密度为1.4 g/cm3的土体的土颗粒排列与正交排列的土骨架模型相近,干密度为1.6 g/cm3和1.7 g/cm3的土体的土颗粒排列与聚合密实排列的土骨架模型相近. 如图8(b)所示,由于Johansen法只考虑了土体相体含量的影响,而没考虑热流在土体中传递的规律,所以计算准确度较低,与实测值差别较大.在-5 ~ 0 ℃时,本研究提出的复合传热法的计算值要小于Johansen法与混合流法的计算值,与实测值较为吻合;在-20 ~ -5 ℃时,复合传热法的计算值要大于混合流法的计算值,小于Johansen法的计算值,整体计算数值处于两种计算方法之间.由此可见,复合传热法的计算精度优于Johansen法,计算精度处于Johansen法与混合流法之间,计算值与实测值之间误差小于10%,符合土工热计算的误差要求. 本研究提出的导热系数计算模型尚存在一定的局限性和适用条件.由于土体干密度决定土体中土颗粒的含量,干密度越大,土颗粒彼此间接触越紧密,所以该计算模型适用于计算饱和、干密度较大的冻土导热系数,对于饱和砂土和粉质黏土较为适用.对于低密度土体,如淤泥质土,土体中未形成有效的土骨架,因此利用该模型计算将会产生一定误差.除此之外,该计算模型未考虑土体级配的影响,对于计算级配较好的冻土导热系数,误差可能较大.影响该模型计算精度的另一个重要原因是冻土未冻水测试结果,未冻水含量测试结果越精确,利用该模型计算的导热系数越准确. 1)考虑土颗粒为均质球体且土颗粒间为球缺接触,给出了正交排列的土颗粒以及聚合密实排列的土颗粒两种土骨架构成形式.计算出了两种排列方式土颗粒体积的计算方法,并给出了土骨架的体积分数表达式.依据表达式中未知数a的取值,可求得不同孔隙率时土骨架的体积含量.同时给出了对应的孔隙冰骨架模型,并依据未冻水含量可计算冻土中孔隙冰和孔隙水体积分数. 2)考虑到土骨架的导热系数与孔隙冰的导热系数相差不大,可以认为热流在土骨架和孔隙冰中的传热过程相互独立.而孔隙水与土骨架、孔隙冰之间存在热量的相互交换,由此构建出包括土-水、冰-水两个热交换过程的复合传热模式.基于建立的复合传热模型以及多孔介质的导热系数经验公式,推导出了相应的导热系数计算模型. 3)通过复合传热法计算不同干密度冻土在不同温度下的导热系数,并与实测值、Johansen法与混合流法计算值进行对比验证.验证结果显示,复合传热法的计算精度处于Johansen法与混合流法之间,优于Johansen法计算精度.在-5 ~ 0 ℃ 温度段内,复合传热法的计算值要略大于实测值,这是由于冻结初始阶段,冻土内未形成贯通的孔隙冰骨架.复合传热法的计算值与实测值误差小于10%,符合误差要求.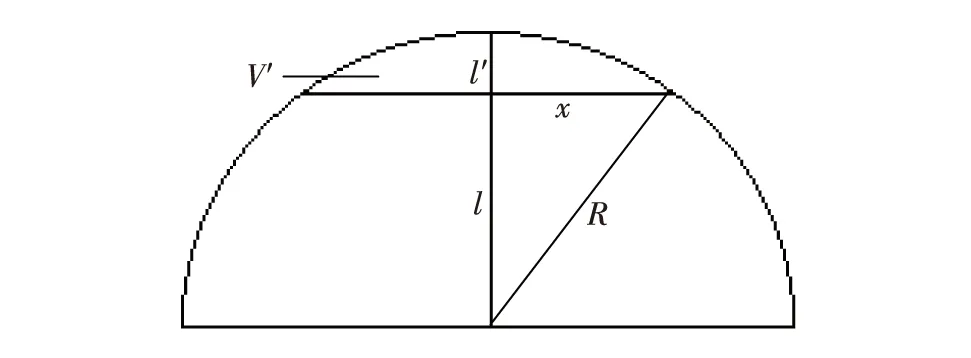
2 土颗粒骨架
2.1 正交排列土骨架

2.2 聚合密实排列土骨架
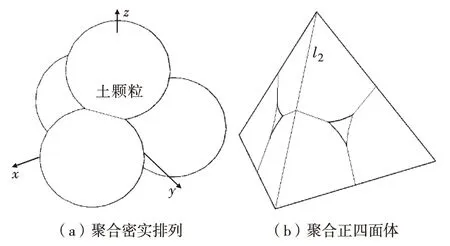
2.3 土骨架体积含量
2.4 孔隙冰骨架
3 导热系数计算模型
3.1 垂直流法与平流法
3.2 复合传热计算模型
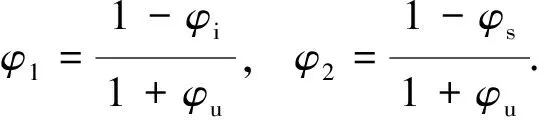
4 对比验证
5 结 论
